CS 627 Elliptic Curves and Cryptography Paper by

CS 627 Elliptic Curves and Cryptography Paper by: Aleksandar Jurisic, Alfred J. Menezes Published: January 1998 Presented by: Sagar Chivate

Background in elliptic curves If p is a prime greater than 3 and Zp is group of non-zero elements under the operation of multiplication modulo p. Zp = {1, 2, …, p-1} Then an elliptic curve E over ZP is defined by the equation: y 2 = x 3 + ax + b where, a, b ∊ Zp and 4 a 3 + 27 b 2 0 (mod p), together with special point O, called as point at infinity.

Example of elliptic curve Let p = 23, a = 1, b = 1 Note: 4 a 3 + 27 b 2 = 8 (mod 23) 0 E : y 2 = x 3 + x + 1 The points on E(Z 23) are O and following: (0, 1) (6, 4) (12, 19) (0, 22) (6, 19) (13, 7) (1, 7) (7, 11) (13, 16) (1, 16) (7, 12) (17, 3) (3, 10) (9, 7) (4, 0) (17, 20) (3, 13) (11, 3) (18, 20) (5, 19) (12, 4) (19, 18) (9, 16) (18, 3) (5, 4) (11, 20) (19, 5)

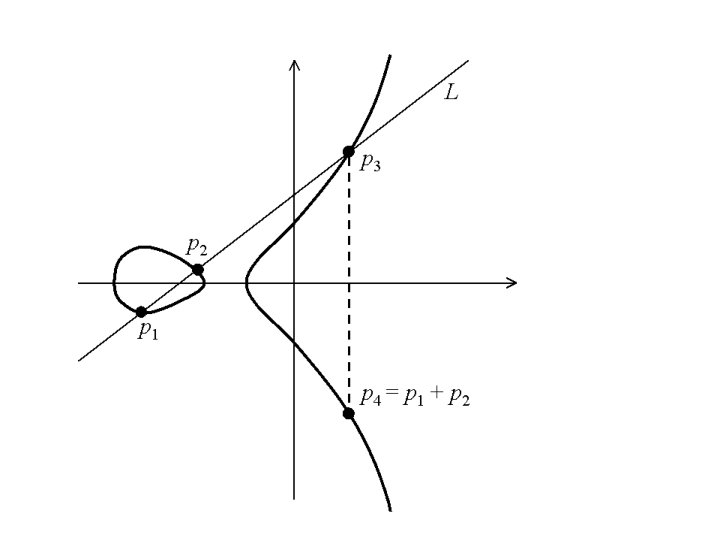
Elliptic curve addition If P, Q ∊ E(Zp) then, 1. P + O = O + P = P 2. If P = (x, y) then –P = (x, -y) 3. and P + (-P) = O 3. If P = (x 1, y 1) and Q = (x 2, y 2) and P -Q then, 4. P + Q = (x 3, y 3) where, 5. x 3 = 2 – x 1 – x 2 6. = y 2 – y 1 Q 7. x 2 – x 1 and y 3 = (x 1 – x 3) – y 1 if P Q, = 3 x 12 + a 2 y 1 if P =

Elliptic curve discrete logarithm problem Select elliptic curve E(Zp) such that the number of points in E are divisible by a large prime n. Then, The “hard” mathematical problem is: Given an elliptic curve E defined over Zp, a point P ∊ E(Zp) of order n, and a point Q ∊ E(Zp), determine the integer d, 0 <= d <= n-1, such that Q = d. P, provided that d exists.

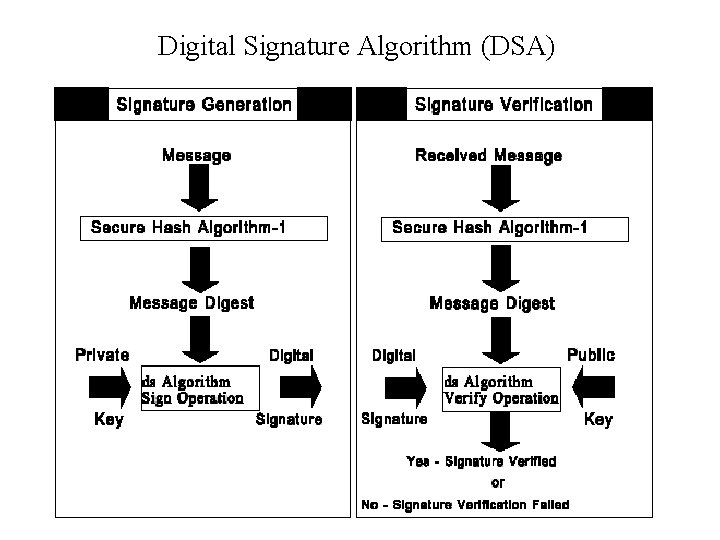
Digital Signature Algorithm (DSA)

Elliptic Curve Digital Signature Algorithm (ECDSA) ECDSA key pair generation: 1. Entity A selects an elliptic curve E defined over Zp. The number of points in E(Zp) should be divisible by a large prime n. 2. Select a point P = E(Zp) of order n. 3. Select a statistically unique and unpredictable integer d in the interval [1, n-1]. 4. Compute Q = d. P. 5. A’s public key is (E, P, n, Q). A’s private key is d.

ECDSA…contd. ECDSA signature generation: 1. Entity A selects a statistically unique and unpredictable integer k in the interval [1, n-1]. 2. Compute k. P = (x 1, y 1) and r = x 1 mod n. To avoid a security condition, r should not equal 0. If r = 0 go to step 1. 3. Compute k-1 mod n. 4. Compute s = k-1 {h(m) + dr} mod n. h is the Secure Hash Algorithm (SHA-1). 5. If s = 0, then go to Step 1. If s = 0, then s-1 mod n does not exist and s-1 is required in the signature verification process. 6. The signature for the message m is the pair of integers (r, s).

ECDSA…contd. ECDSA signature verification: 1. Entity B obtains an authentic copy of Entity A’s public key (E, P, n, Q). 2. Verify that r and s are integers in the interval [1, n-1]. 3. Compute w = s-1 mod n and h(m). 4. Compute u 1 = h(m)w mod n and u 2 = rw mod n. 5. Compute u 1 P + u 2 Q = (x 0, y 0) and v = x 0 mod n. 6. Entity B accepts the signature if and only if v =r.

Security Issues • The best algorithm known to date is Pollard rho-method which takes about n / 2 steps, where a step is an elliptic curve addition. • Software attacks Size of n (in bits) 160 234 426 n / 2 280 2117 2213 MIPS years 9. 6*1011 1. 6*1023 1. 0*1052 • Hardware attacks Build a hardware for a parallel search using Pollard rho-method.

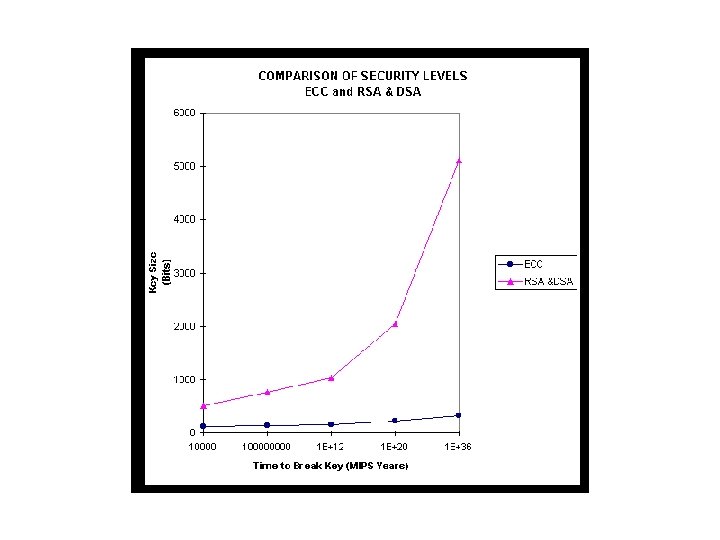
Advantages of ECC • Equivalent ECC key size is 160 bits as compared to 1024 bit size of RSA • ECC does not require prime numbers and exponential processing for encryption. • ECC offers considerable bandwidth savings when being used to transform short messages. Disadvantages of ECC • Hyper-elliptic cryptosystems offer even smaller key sizes • ECC is mathematically more difficult to explain to client • Confidence level in ECC is not as high as RSA

Applications Elliptic curves are used in: • Factoring integers • Primality proving • Public key cryptography Implementations of ECC are particularly beneficial in applications where bandwidth, processing capacity, power availability, or storage is constrained. Such applications include: • Wireless transactions • Handheld computing • Broadcast and • Smart card applications.

Conclusion • Elliptic Curves should receive rigorous testing before it is actually implemented in large networks, but it should provide a solution to many of the problems facing public-key encryption in general.

Thank you!