CS 615 Design Analysis of Algorithms Chapter 1

CS 615: Design & Analysis of Algorithms Chapter 1: Introduction, Algorithmic Notation and Flowcharts

Course Content 1. Introduction, Algorithmic Notation and Flowcharts (Brassard & Bratley, Chap. 3) 2. Efficiency of Algorithms (Brassard & Bratley, Chap 2) 3. Basic Data Structures (Brassard & Bratley, Chap. 5) 4. Sorting (Weiss, Chap. 7) 5. Searching (Brassard & Bratley, Chap. 9) 6. Graph Algorithms (Weiss, Chap. 9) 7. Randomized Algorithms (Weiss, Chap. 10) 8. String Searching (Sedgewick, Chap. 19) 9. NP Completeness (Sedgewick, Chap. 40) 6/14/2021 CS 615 Design & Analysis of Algorithms 2

Content Text books, Lectures Assessments Asymptotic Notation for “the order of” Maximum Rule Flowcharts Basic Flowchart Constructions 6/14/2021 CS 615 Design & Analysis of Algorithms 3

Instructor Yusuf Altunel Email: y. altunel@iku. edu. tr Web: http: //web. iku. edu. tr/~yaltunel Tel: (212) 498 42 10 6/14/2021 CS 615 Design & Analysis of Algorithms 4

Text Books Main Resources Data Structures and Algorithm Analysis in C, 2 nd Edition; Mark Allen Weiss; Addison Wesley Longman, 1997 Fundamentals of Algorithmics; Gilles Brassard & Paul Bratley; Prentice. Hall, 1996. Data Structures, Algorithms & Software Principles, Thomas A. Standish, Addison Wesley, 1995. Other Resources Algorithms, Richard Johnsonbaugh and Marcus Schaefer, Pearson, 2004, ISBN 0 -02 -360692 -4. http: //condor. depaul. edu/~rjohnson/algorithm/index. html Algorithm Design: Foundations, Analysis, and Internet Examples; Michael T. Goodrich & Roberto Tamassia; Wiley, 2002, ISBN 978 -0 -471 -38365 -9. http: //ww 3. algorithmdesign. net/ Algorithms, Robert Sedgewick, Addison-Wesley 1983, e-book. 6/14/2021 CS 615 Design & Analysis of Algorithms 5

Lectures Courses and labs Day Hours Location Theory Thu 11: 00 -12: 45 (2 Hours) Lab 251 Lab Fri 11: 00 -12: 45 (2 Hours) Lab 251 6/14/2021 CS 615 Design & Analysis of Algorithms 6

Follow up the course Use the web page of the course http: //web. iku. edu. tr/~yaltunel/Spring 2005/CS 615 Use the email group of the course Send an empty email to subscribe: CS_615 -subscribe@yahoogroups. com To send a message: CS_615@yahoogroups. com To access on web: http: //groups. yahoo. com/group/CS_615 6/14/2021 CS 615 Design & Analysis of Algorithms 7

Assessment Participation %10 Project %30 Mid. Term %30 Final • Please take care of the rules and regulations of the University. • Otherwise you might be reported to the faculty, as well as lose all bonus options of this course. %40 Bonus Grading: %110 %10 Bonus 6/14/2021 CS 615 Design & Analysis of Algorithms 8

Project A real world application with dynamically constructed graph should be implemented until the end of the semester! Details will be announced later! 6/14/2021 CS 615 Design & Analysis of Algorithms 9

Algorithmic Notation and Flowcharts (Brassard & Bratley Chp: Chapter 3) 6/14/2021 CS 615 Design & Analysis of Algorithms 10

Asymptotatic Notation Used to express The time taken by an algorithm Within a multiplicative constant Permits Simplification in measuring other tangible things Deals with The behavior of functions in the limits For sufficiently large parameters An asymptotically superior algorithm is very often preferable 6/14/2021 CS 615 Design & Analysis of Algorithms 11

Notation for “the order of” f: N R 0 be an arbitrary function from the natural numbers to the nonnegative numbers The mathematical symbol order of is denoted by O(f(n)) the set of all functions t: N R 0 such that t(n) cf(n) for all n n 0 O(f(n))={t: N R 0 |( c R+)( n N)[t(n) cf(n)]} Examples f(n)=n 3 -3 n 2 -n-8 O(n 3) f(n)= n 3 O(n 3) Maximum Rule: Let f, g: N R 0 be two arbitrary functions O(f(n), g(n))=O(max(f(n), g(n))) 6/14/2021 CS 615 Design & Analysis of Algorithms 12

Example for Maximum Rule An algorithm that proceeds in three steps: Initialization Take time in O(n 2) Processing Take time in O(n 3) Finalization Take time in O(nlogn) The complete algorithm takes time in O(n 2 + n 3 + nlogn) = O(max(n 2, n 3, nlogn)) =O(n 3) 6/14/2021 CS 615 Design & Analysis of Algorithms 13

Results of Maximum Rule If t(n) is a complicated function the most significant term of t(n) gives the order of function discarding its coefficient Example: f(n)= 12 n 3 - 5 n 2 + logn + 36 O(f(n))=O(n 3) f(n)= 999999 n 94 - 345 n 35 + 1 O(f(n))=O(n 94) 6/14/2021 CS 615 Design & Analysis of Algorithms 14

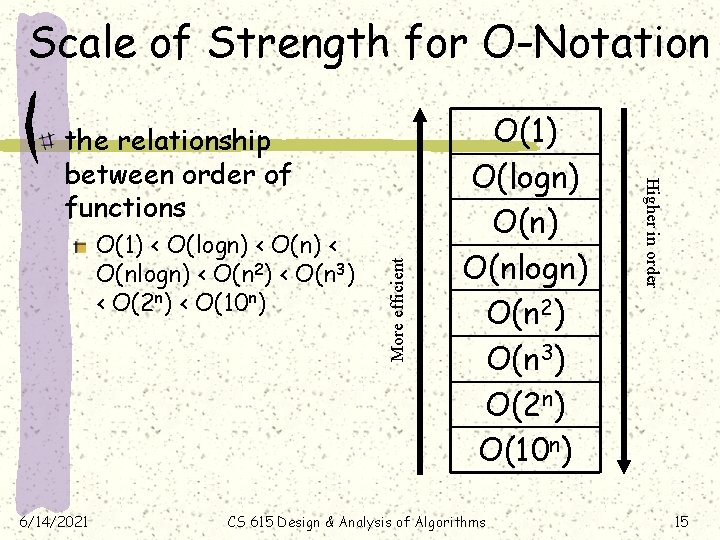
Scale of Strength for O-Notation 6/14/2021 More efficient O(1) < O(logn) < O(nlogn) < O(n 2) < O(n 3) < O(2 n) < O(10 n) O(1) O(logn) O(nlogn) O(n 2) O(n 3) O(2 n) O(10 n) CS 615 Design & Analysis of Algorithms Higher in order the relationship between order of functions 15

Examples What is the order of 18 nlog 2 n + 19 n + 3 =O(18 nlog 2 n + 19 n + 3) =O(max (nlogn, n, 3) ) =O(nlogn) What is the order of n 4 + 2 n + 3 nlogn + 3 =O(n 4 + 2 n + 3 nlogn + 3) =O(max (n 4, 2 n, nlogn , 3) ) =O(2 n) 6/14/2021 CS 615 Design & Analysis of Algorithms 16

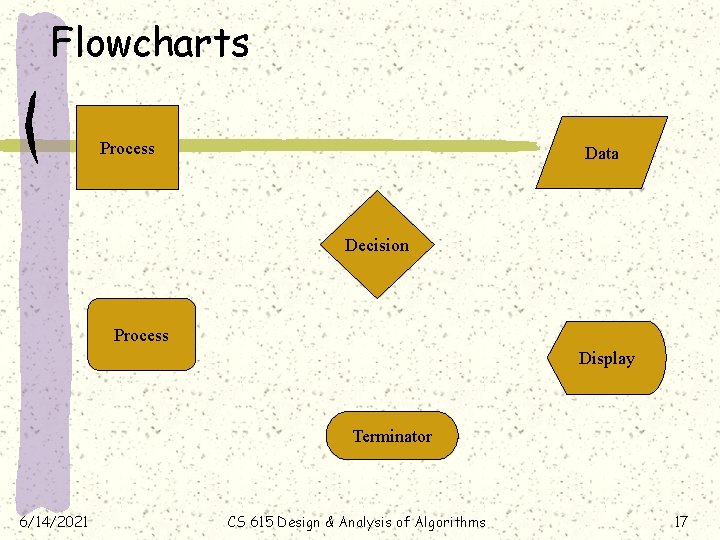
Flowcharts Process Data Decision Process Display Terminator 6/14/2021 CS 615 Design & Analysis of Algorithms 17

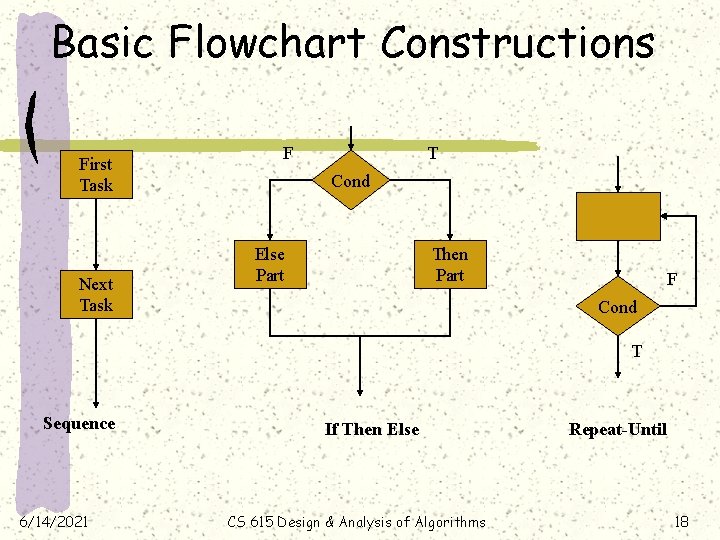
Basic Flowchart Constructions First Task Next Task F T Cond Else Part Then Part F Cond T Sequence 6/14/2021 If Then Else CS 615 Design & Analysis of Algorithms Repeat-Until 18

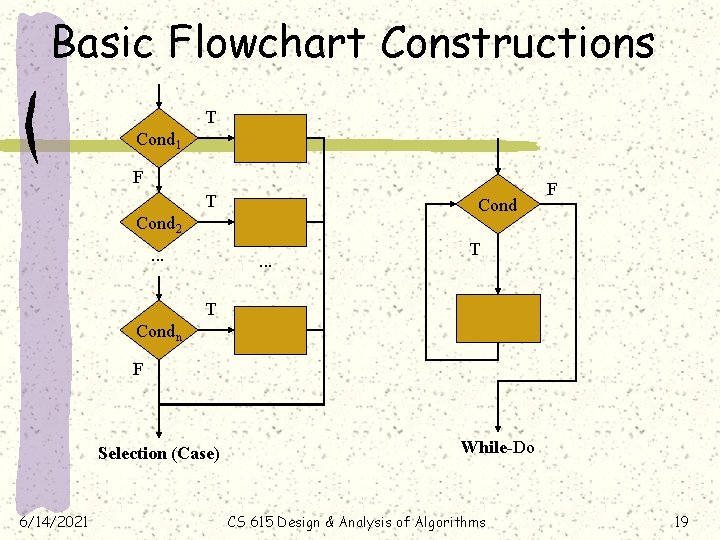
Basic Flowchart Constructions T Cond 1 F T Cond 2. . . F T T Condn F Selection (Case) 6/14/2021 While-Do CS 615 Design & Analysis of Algorithms 19

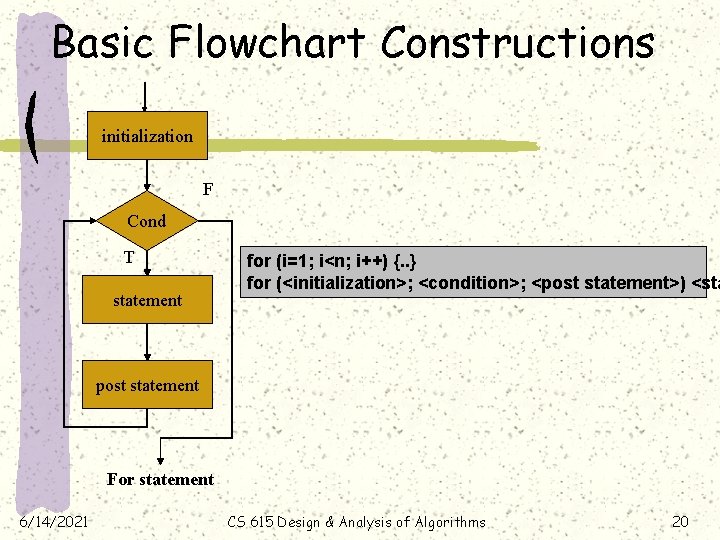
Basic Flowchart Constructions initialization F Cond T statement for (i=1; i<n; i++) {. . } for (<initialization>; <condition>; <post statement>) <sta post statement For statement 6/14/2021 CS 615 Design & Analysis of Algorithms 20

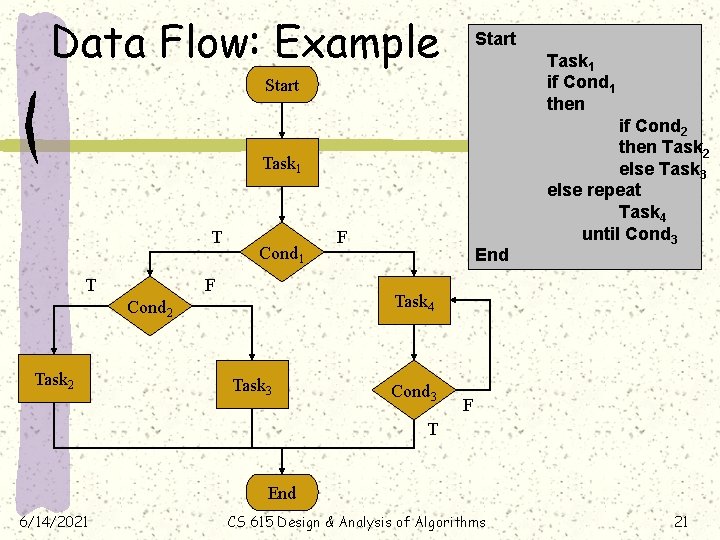
Data Flow: Example Start Task 1 if Cond 1 then Start Task 1 T T Cond 1 F End Task 4 Cond 2 Task 2 F if Cond 2 then Task 2 else Task 3 else repeat Task 4 until Cond 3 Task 3 Cond 3 F T End 6/14/2021 CS 615 Design & Analysis of Algorithms 21

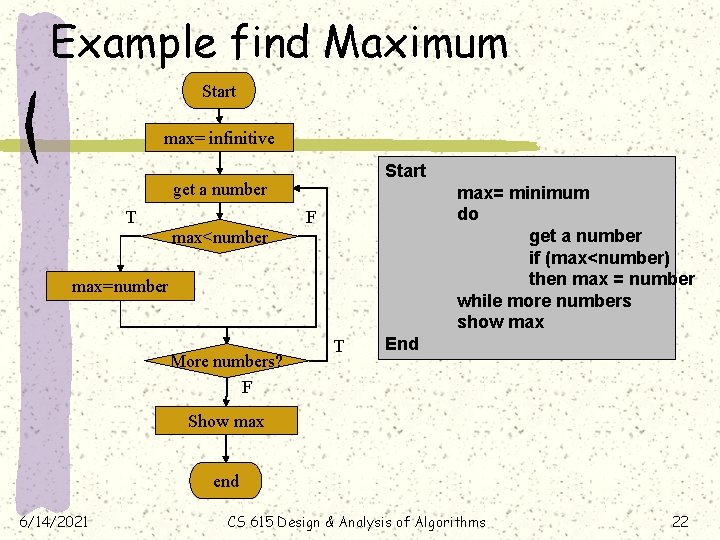
Example find Maximum Start max= infinitive Start get a number T max<number max= minimum do get a number if (max<number) then max = number while more numbers show max F max=number T More numbers? F T End Show max end 6/14/2021 CS 615 Design & Analysis of Algorithms 22

End of Chapter 1 Introduction, Algorithmic Notation and Flowcharts 6/14/2021 CS 615 Design & Analysis of Algorithms 23