CS 61 CL Machine Structures Lec 6 Number

CS 61 CL Machine Structures Lec 6 – Number Representation David Culler Electrical Engineering and Computer Sciences University of California, Berkeley

Review: MIPS R 3000 r 1 ° ° ° r 31 PC lo hi 0 Programmable storage Data types ? 2^32 x bytes Format ? 31 x 32 -bit GPRs (R 0=0) Addressing Modes? 32 x 32 -bit FP regs (paired DP) HI, LO, PC Arithmetic logical Add, Add. U, Sub. U, And, Or, Xor, Nor, SLTU, Add. IU, SLTIU, And. I, Or. I, Xor. I, LUI SLL, SRA, SLLV, SRAV Memory Access LB, LBU, LHU, LWL, LWR SB, SH, SWL, SWR Control 32 -bit instructions on word boundary J, JAL, JR, JALR BEq, BNE, BLEZ, BGTZ, BLTZ, BGEZ, BLTZAL, BGEZAL 9/15/2020 cs 61 cl f 09 lec 6 2

MIPS Instruction Format R: Reg-Reg I: Reg-Imed J: Jump op rs rt rd shamt funct 6 5 5 6 op rs rt immediate 6 5 5 16 op immediate 6 26 • Reg-Reg instructions (op == 0) – add, sub, and, or, nor, xor, slt – sll. srl, sra R[rd] : = R[rs] funct R[rt]; pc: =pc+4 R[rd] : = R[rt] shft shamt • Reg-Immed (op != 0) – – addi, andi, ori, xori, lui, addiu, sltiu lw, lhu, lbu sw, sh, sb 9/15/2020 R[rt] : = R[rs] op Im 16 R[rt] : = Mem[ R[ rs ] + sign. Ex(Im 16) ]* Mem[ R[ rs ] + sign. Ex(Im 16) ] : = R[rt] cs 61 cl f 09 lec 6 3

Computer Number Systems • We all take positional notation for granted – Dk-1 Dk-2 …D 0 represents Dk-1 Bk-1 + Dk-2 Bk-2 + …+ D 0 B 0 where B { 0, …, B-1 } • We all understand how to compare, add, subtract these numbers – Add each position, write down the position bit and possibly carry to the next position • Computers represent finite number systems – Generally radix 2 – Bk-1 Bk-2 …B 0 represents Bk-12 k-1 + B-22 k-2 + …+ B 0 20 where B { 0, 1 } 9/15/2020 cs 61 cl f 09 lec 6 4

Unsigned Numbers - Addition +15 +14 1111 +0 1110 +13 0001 + 1101 Example: 3 + 2 = 5 +1 0000 +2 0010 Is just addition, base 2 +12 1100 0011 +3 +11 1011 0100 +4 1010 0101 +10 1001 +9 0110 1000 +8 9/15/2020 0111 Unsigned binary addition Add the bits in each position and carry +5 1 0011 + 0010 +6 0101 +7 cs 61 cl f 09 lec 6 5

Number Systems • Desirable properties: – Efficient encoding (2 n bit patterns. How many numbers? ) – Positive and negative » Closure (almost) under addition and subtraction • Except when overflow » Representation of positive numbers same in most systems » Major differences are in how negative numbers are represented – Efficient operations » Comparison: =, <, > » Addition, Subtraction Which one did you learn in 2 nd » Detection of overflow grade? – Algebraic properties? » Closure under negation? » A == B iff A – B == 0 • Three Major schemes: – sign and magnitude – ones complement – twos complement – (excess notation) 9/15/2020 cs 61 cl f 09 lec 6 6

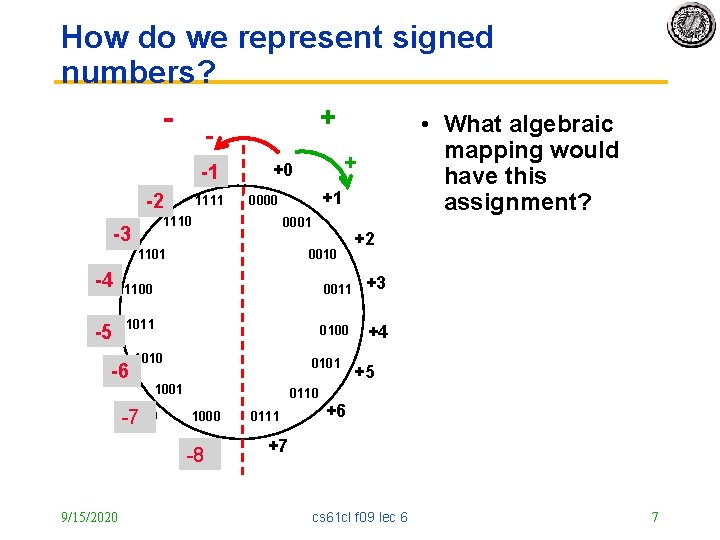
How do we represent signed numbers? - + +15 -1 +14 -2 1111 +13 -3 + +0 +1 0000 1110 • What algebraic mapping would have this assignment? 0001 1101 0010 +2 +12 -4 1100 0011 +3 +11 -5 1011 0100 +4 1010 +10 -6 0101 1001 -7+9 0110 1000 +8 -8 9/15/2020 0111 +5 +6 +7 cs 61 cl f 09 lec 6 7

Twos Complement Bk-1 Bk-2 …B 0 represents -Bk-12 k-1 + B-22 k-2 + …+ B 0 20 9/15/2020 cs 61 cl f 09 lec 6 8

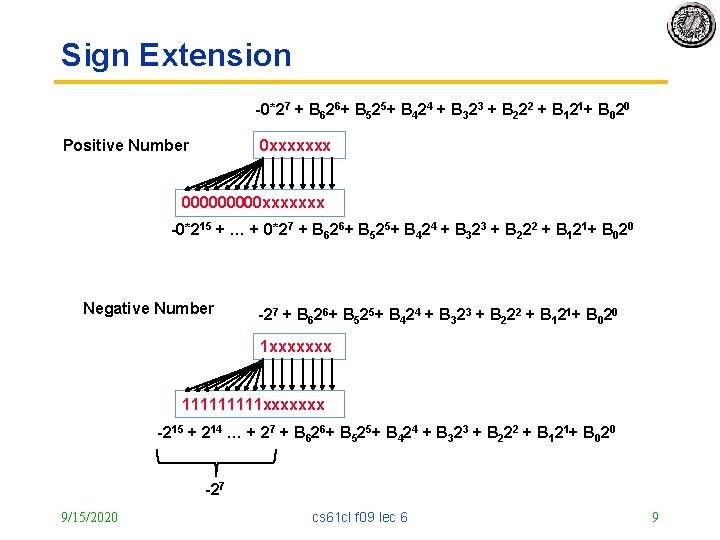
Sign Extension -0*27 + B 626+ B 525+ B 424 + B 323 + B 222 + B 121+ B 020 Positive Number 0 xxxxxxx 00000 xxxxxxx -0*215 + … + 0*27 + B 626+ B 525+ B 424 + B 323 + B 222 + B 121+ B 020 Negative Number -27 + B 626+ B 525+ B 424 + B 323 + B 222 + B 121+ B 020 1 xxxxxxx 11111 xxxxxxx -215 + 214 … + 27 + B 626+ B 525+ B 424 + B 323 + B 222 + B 121+ B 020 -27 9/15/2020 cs 61 cl f 09 lec 6 9

MIPS Instruction Format R: Reg-Reg I: Reg-Imed J: Jump op rs rt rd shamt funct 6 5 5 6 op rs rt immediate 6 5 5 16 op Addr 6 26 • Reg-Reg instructions (op == 0) • Reg-Immed (op != 0) • Jumps – jal – jr PC : = PC 31. . 28 || addr || 00; R[31] : = PC + 4 PC : = R[rs] 9/15/2020 cs 61 cl f 09 lec 6 10

MIPS Instruction Format R: Reg-Reg I: Reg-Imed J: Jump • • op rs rt rd shamt funct 6 5 5 6 op rs rt immediate 6 5 5 16 op Addr 6 26 Reg-Reg instructions (op == 0) Reg-Immed (op != 0) Jumps Branches – BEQ, BNE PC : = (R[rs] ? = R[rt]) ? PC + sign. Ex(im 16) : PC+4 – BLT, BGT, BLE, BGTE are pseudo ops – Move and LI are pseudo ops too 9/15/2020 cs 61 cl f 09 lec 6 11

So what about subtraction? +15 +14 1111 +0 1110 +13 +1 0000 0001 - 1101 +2 0010 +12 1100 0011 +3 +11 1011 0100 +4 1010 0101 +10 1001 +9 0110 1000 +8 9/15/2020 0111 • Subtraction – or addition of a negative number – should move “backwards” on the number wheel? +5 +6 +7 cs 61 cl f 09 lec 6 12

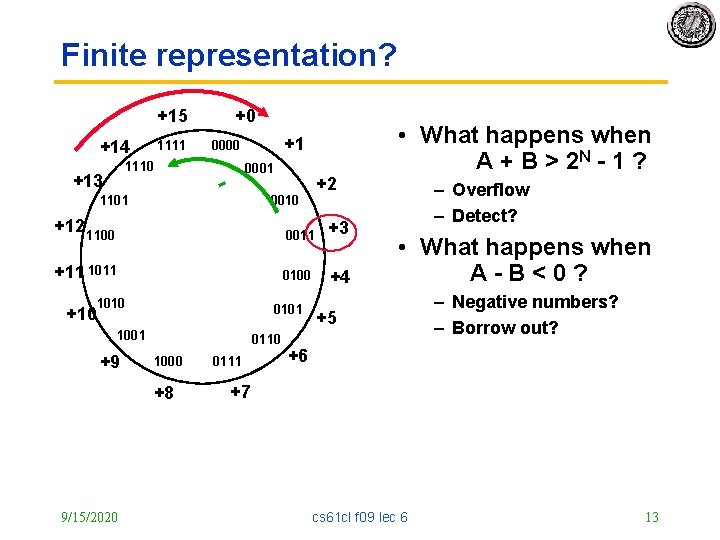
Finite representation? +15 +14 1111 1110 +13 1101 +0 +1 0000 0001 - +2 0010 +12 1100 0011 +3 +11 1011 0100 +4 1010 0101 +10 1001 +9 0110 1000 +8 9/15/2020 0111 • What happens when A + B > 2 N - 1 ? – Overflow – Detect? • What happens when A-B<0? +5 – Negative numbers? – Borrow out? +6 +7 cs 61 cl f 09 lec 6 13

Administrative Issues • HW 5 is due tonight before midnight • Proj 1 is due Friday – your submission must build by running make in the directory containing the source files - that is what the autograder does – you should confirm that it passes proj 1. tests/test. proj 1 – autograder will run additional tests, so generate your own » feel free to share them » can run reference asm 16 to generate. o and. syms • Midterm is wed 10/7 in 10 evans – alternate is mon 10/5 in 310 Soda, send email, and do poll – review session is Sunday evening (TBA) – homework this week is to study previous midterms • Monday office hours moved to tues 9 -11 in QC 3 9/15/2020 cs 61 cl f 09 lec 6 14

Can’t get enough C fun&games… • Write a program in C that reproduces itself – the output is the text of the program – you can compile the output with gcc and it will produce a program that reproduces itself… • Hint: – Write the following sentence twice, the second in quotes. “Write the following sentence twice, the second in quotes. ” – it is way easier in scheme 9/15/2020 cs 61 cl f 09 lec 6 15

Other choices for negative numbers 9/15/2020 cs 61 cl f 09 lec 6 16

Sign and Magnitude -7 -6 -5 1111 1110 +0 +1 0000 0001 1101 0010 +2 + -4 1100 0011 +3 -3 1011 0100 +4 -2 1010 0101 1001 -1 0110 1000 -0 0111 0 100 = + 4 Example: N = 4 1 100 = - 4 +5 - +6 +7 High order bit is sign: 0 = positive (or zero), 1 = negative Remaining low order bits is the magnitude: 0 (000) thru 7 (111) Number range for n bits = +/- 2 n-1 - 1 Representations for 0? Operations: =, <, >, +, - ? ? ? 9/15/2020 cs 61 cl f 09 lec 6 17

Ones Complement Bit manipulation: simply complement each of the bits 0111 -> 1000 Algebraically … N is positive number, then N is its negative 1's complement N = (2 n - 1) - N 24 10000 -1 - 00001 Example: 1's complement of 7 1111 -7 - 0111 1000 -7 in 1's comp. 9/15/2020 cs 61 cl f 09 lec 6 18

Ones Complement on the number wheel Subtraction implemented by addition & 1's complement Sign is easy to determine Closure under negation. If A can be represented, so can -A Still two representations of 0! If A = B then is A – B == 0 ? 9/15/2020 is almost clockwise cs 61 cl f 09 lec 6 like unsigned Addition advance, 19

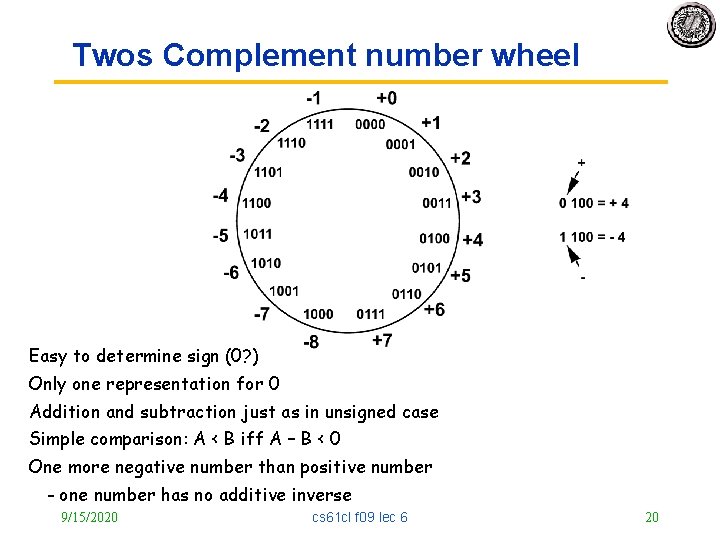
Twos Complement number wheel Easy to determine sign (0? ) Only one representation for 0 Addition and subtraction just as in unsigned case Simple comparison: A < B iff A – B < 0 One more negative number than positive number - one number has no additive inverse 9/15/2020 cs 61 cl f 09 lec 6 20

Twos Complement (algebraically) N* = 2 n - N 4 2 = 10000 Example: Twos complement of 7 sub 7 = 0111 1001 = repr. of -7 4 2 = 10000 Example: Twos complement of -7 sub -7 = 1001 0111 = repr. of 7 Bit manipulation: Twos complement: take bitwise complement and add one 0111 -> 1000 + 1 -> 1001 (representation of -7) 1001 -> 0110 + 1 -> 0111 (representation of 7) 9/15/2020 cs 61 cl f 09 lec 6 21

How is addition performed in each number system? • Operands may be positive or negative 9/15/2020 cs 61 cl f 09 lec 6 22

Twos Complement Addition Perform unsigned addition and Discard the carry out. 4 0100 -4 1100 +3 0011 + (-3) 1101 7 0111 -7 11001 Overflow? 4 0100 -4 1100 -3 1101 +3 0011 1 10001 -1 1111 Simpler addition scheme makes twos complement the most common choice for integer number systems within digital systems 9/15/2020 cs 61 cl f 09 lec 6 23

Sign Magnitude Addition Operand have same sign: unsigned addition of magnitudes result sign bit is the same as the operands' sign 4 0100 -4 1100 +3 0011 + (-3) 1011 7 0111 -7 1111 Operands have different signs: subtract smaller from larger and keep sign of the larger 4 -3 1 9/15/2020 0100 -4 1100 1011 +3 0011 0001 -1 1001 cs 61 cl f 09 lec 6 24

Ones complement addition Perform unsigned addition, then add in the end-around carry 4 0100 -4 1011 +3 0011 + (-3) 1100 7 0111 -7 10111 End around carry 1 1000 4 0100 -4 1011 -3 1100 +3 0011 1 10000 -1 1110 End around carry 1 9/15/2020 0001 cs 61 cl f 09 lec 6 25

2 s Comp: ignore the carry out -M + N when N > M: M* + N = (2 n - M) + N = 2 n + (N - M) Ignoring carry-out is just like subtracting 2 n -M + -N where N + M ≤ 2 n-1 n n -M + (-N) = M* + N* = (2 - M) + (2 - N) n n = 2 - (M + N) + 2 After ignoring the carry, this is just the right twos compl. representation for -(M + N)! 9/15/2020 cs 61 cl f 09 lec 6 26

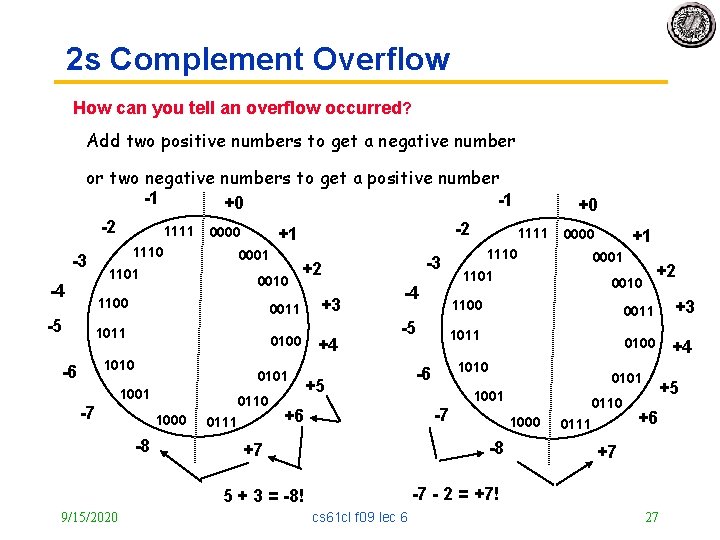
2 s Complement Overflow How can you tell an overflow occurred? Add two positive numbers to get a negative number or two negative numbers to get a positive number -1 -1 +0 -2 -2 1111 0000 1111 +1 1110 -3 1101 -4 -5 0001 0010 1100 0011 1011 0100 1010 -6 +2 +3 0101 1001 -7 1000 -8 0110 0111 +4 1101 -4 -5 +5 0001 1010 -6 +2 0010 1011 0011 +3 0100 +4 0101 1000 -8 +7 +1 0000 1100 -7 +6 0110 0111 +5 +6 +7 -7 - 2 = +7! 5 + 3 = -8! 9/15/2020 1110 -3 +0 cs 61 cl f 09 lec 6 27

2 s comp. Overflow Detection 5 0111 0101 -7 1000 1001 3 0011 -2 1100 -8 1000 7 10111 Overflow 5 0000 0101 -3 1111 1101 2 0010 -5 1011 7 0111 -8 11000 No overflow Overflow occurs when carry in to sign does not equal carry out 9/15/2020 cs 61 cl f 09 lec 6 28