CS 6045 Advanced Algorithms Sorting Algorithms Heap Data

CS 6045: Advanced Algorithms Sorting Algorithms

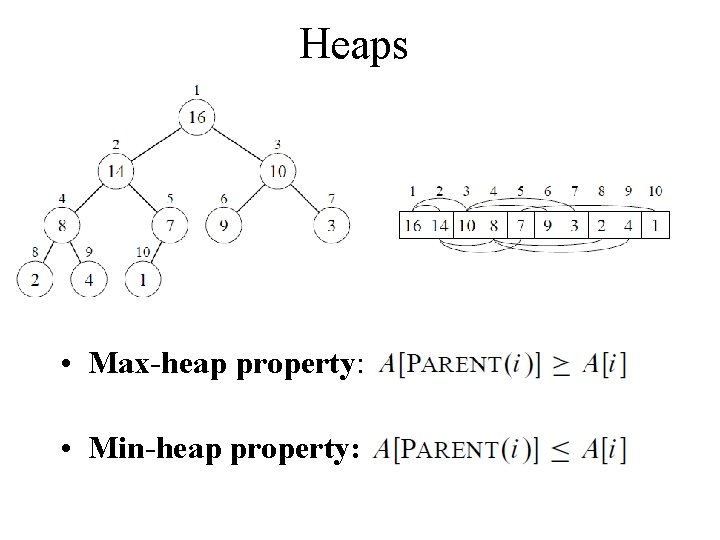
Heap Data Structure • A heap (nearly complete binary tree) can be stored as an array A – Root of tree is A[1] – Parent of – Left child of A[i] = A[2 i] – Right child of A[i] = A[2 i + 1] – Computing is fast with binary representation implementation

Heaps • Max-heap property: • Min-heap property:

Maintain the Heap Property • Running Time? • O(log n)

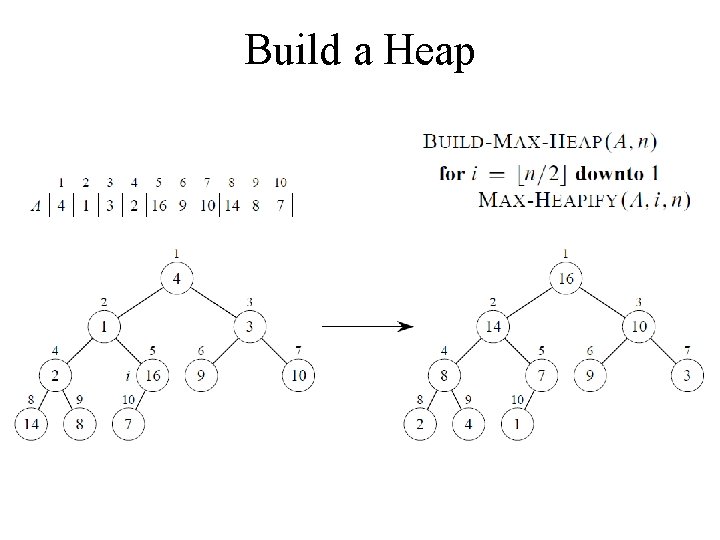
Build a Heap

Correctness • Loop invariant: At start of every iteration of for loop, each node i+1, i+2, …, n is the root of a max-heap • Analysis running time? • O(n log n) • Tighter bound? O(n)

Heapsort

Analysis • • • BUILD-MAX-HEAP: O(n) for loop: n – 1 times Exchange elements: O(1) MAX-HEAPIFY: O(log n) Time: – O(n log n)

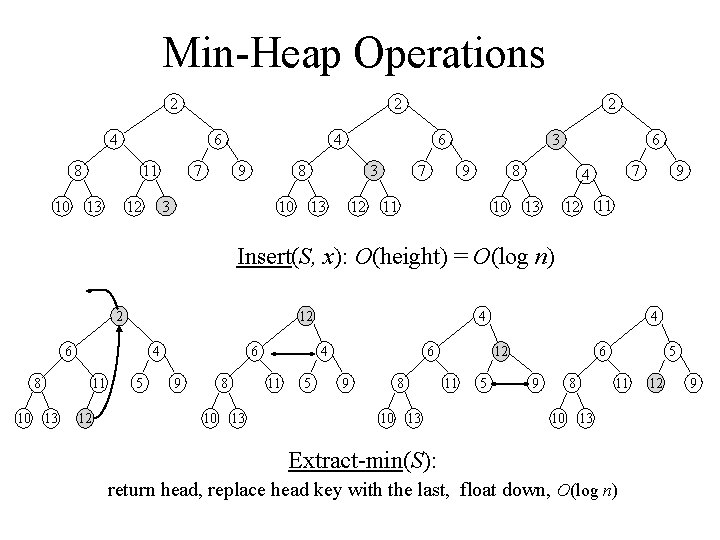
Min-Heap Operations 2 2 4 8 6 11 10 13 7 4 9 6 8 3 12 2 10 3 13 12 7 6 3 9 8 11 10 7 4 13 12 9 11 Insert(S, x): O(height) = O(log n) 2 12 6 8 10 13 4 11 12 5 6 9 8 10 13 4 4 11 5 6 9 8 10 13 4 12 11 5 6 9 8 5 11 10 13 Extract-min(S): return head, replace head key with the last, float down, O(log n) 12 9

Priority Queues • Priority Queue – Maintains a dynamic set S of elements – Each element has a key --- an associated value • Applications – job scheduling on shared computer – Dijkstra’s finding shortest paths in graphs – Prim’s algorithm for minimum spanning tree

Priority Queues • Operations supported by priority queue – Insert(S, x) - inserts element with the pointer x – Minimum/Maximum(S) - returns element with the minimum key – Extract-Min/Max(S) - removes and returns minimum key – Increase/Decrease-Key(S, x, k) – increases/decreases the value of element x’s key to the new value k

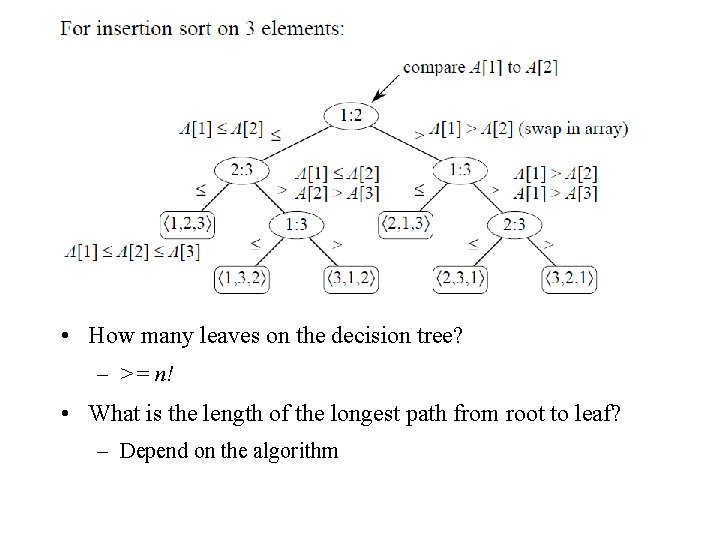
Comparison Sorting • The only operation that may be used to gain order information about a sequence is comparison of pairs of elements • Insertion sort, merge sort, quicksort, heapsort • Lower bound for comparison sorting?

Decision Tree Model • Abstraction of any comparison sort • Counting only comparisons • Abstract everything else: such as control and data movement

• How many leaves on the decision tree? – >= n! • What is the length of the longest path from root to leaf? – Depend on the algorithm

Lower Bound for Comparison Sorting • A lower bound on the heights of decision trees in the lower bound on the running time of any comparison sort algorithm • (n log n) – n! <= l <= 2 h >= n! h >= lg(n!) >= lg (n/e)n //Stirlling’s approximation = nlg(n/e) = nlgn – nlge = (n log n)

Non-comparison Sorts • Counting Sort

Analysis • O(n + k) • How big a k is practical?

Radix Sort

Correctness • Induction on number of passes (i in pseudocode). • Assume digits 1, 2, ……, i -1 are sorted. • Show that a stable sort on digit i leaves digits 1, 2, ……, i sorted: – If 2 digits in position i are different, ordering by position i is correct, and positions 1, 2, …… , i - 1 are irrelevant. – If 2 digits in position i are equal, numbers are already in the right order (by inductive hypothesis). The stable sort on digit i leaves them in the right order.

Analysis • O(n + k) per iteration • d iterations • O(d(n + k)) total

Bucket Sort • Idea: – Divide [0, 1) into n equal-sized buckets – Distribute the n input values into the buckets – Sort each bucket – Go through buckets in order, listing elements in each on