CS 575 Design and Analysis of Computer Algorithms

CS 575 Design and Analysis of Computer Algorithms Professor Michal Cutler Lecture 5 September 13, 2005

This class Recursion tree method l Substitution method l Iteration l The master theorem l Application examples of Master theorem l

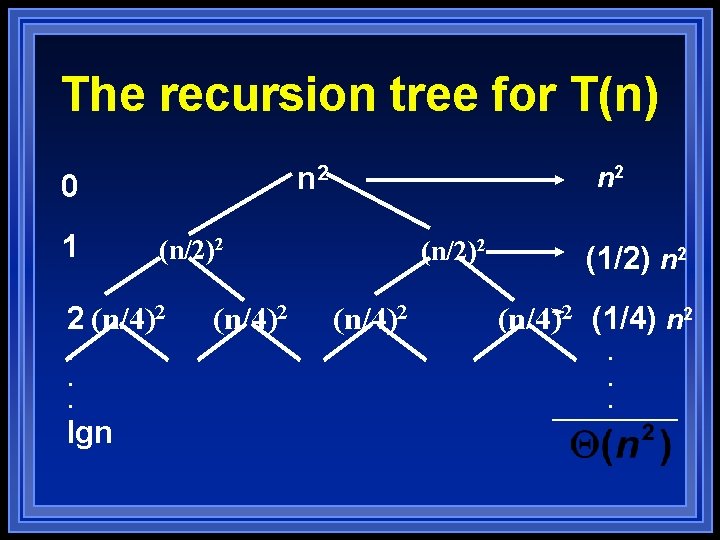
Recursion trees l l The tree is expanded one depth at a time. In the result tree: – Each “recursive call” is represented by a node containing the “non recursive” number of operations done during the call (t(size)) – Each base case is represented by a leaf containing the count for the base case l The number of operations is summed for each depth, and then over the depths

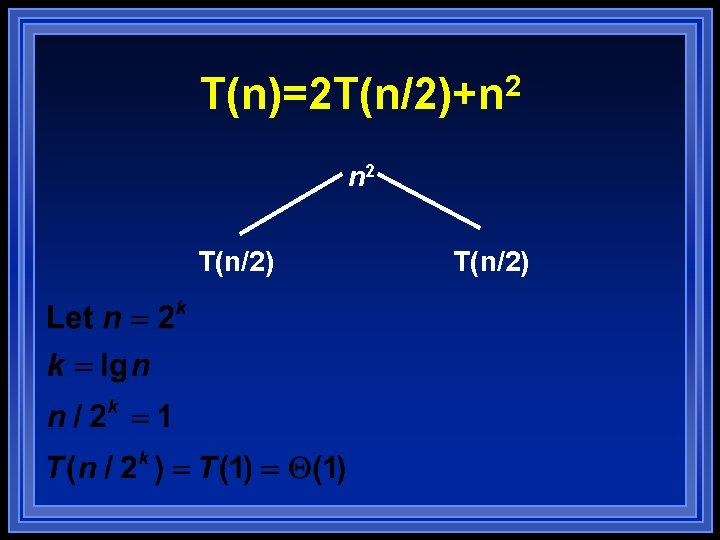
T(n)=2 T(n/2)+n 2 T(n/2)

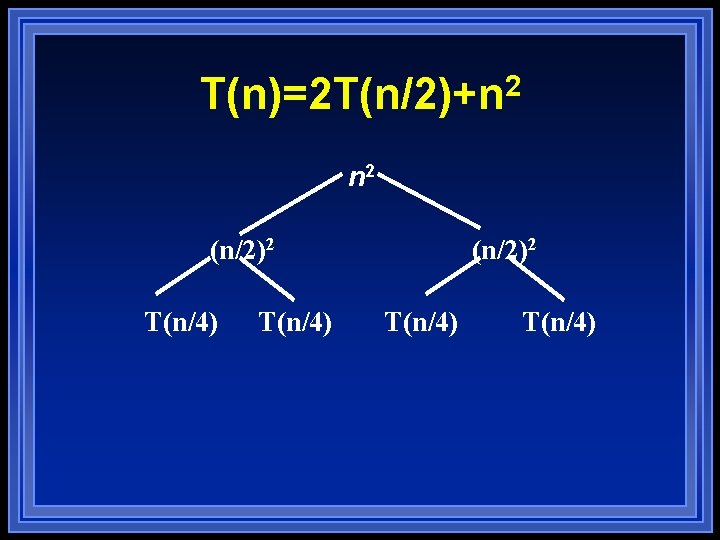
T(n)=2 T(n/2)+n 2 (n/2)2 T(n/4)

The recursion tree for T(n) n 2 0 1 (n/2)2 2 (n/4)2 . . . lgn n 2 (n/4)2 (n/2)2 (n/4)2 (1/2) n 2 (n/4)2 (1/4) n 2 . . .

Recursion trees

Recursion trees

The substitution method l l l We guess the form of the solution (from experience mostly). We then verify the solution and solve for constants. Not possible to guess correctly in every case. T(n) = 4 T(n/2) + n We guess O(n 3) and show T(n) cn 3 for all n n 0

Example (cont. ) l We assume that T(k) ck 3 for k < n and prove T(n) cn 3 by induction. T(n)=4 T(n/2) + n 4 c(n/2)3 + n = = (c/2)n 3 + n = cn 3 - ((c/2)n 3 - n) cn 3 provided (c/2)n 3 - n 0 l So (c/2)n 3 n and c 2/n 2 for all n 1 l c 2 and n 1

Initial Condition Assume that T(1)=3 l 3=T(1) c 13=c. So c max{3, 2}=3. l

A tighter bound Improve bound to T(n)=O(n 2) l We assume that T(k) ck 2 for k < n and prove T(n) cn 2. l T(n)=4 T(n/2) + n 4 c(n/2)2 + n = = cn 2 + n. l Bad guess! Try T(n) c 1 n 2 -c 2 n

Subtract a lower term l We assume that T(k) c 1 k 2 -c 2 k for k < n and prove T(n) c 1 n 2 -c 2 n. T(n)=4 T(n/2) + n 4(c 1(n/2)2 - c 2 n/2)+ n = (c 1 n 2 - c 2 n) - (c 2 n - n) (c 1 n 2 - c 2 n) only if c 2 n- n 0 and c 2 1 for n 1 l Since T(1)=3 c 112 - c 21 we pick c 1=4 and c 2=1

The iteration method l We expand the recursion, then get a summation, then compute the summation using algebraic methods.

The iteration method l We have to know rules for summations to use this method. l We often use this method to guess the solution for the substitution method.

Example T(n) = n + 4 T(n/2) = n + 4(n/2 + 4 T(n/4))= = n + 2 n + 16(n/4 + 4 T(n/8))= = n + 2 n + 4 n + 64(n/8 + 4 T(n/16))= = n + 22 n + 23 n + …+2 k-1 n + 4 k. T(n/2 k) l Let n=2 k and k=lgn l We know 4 lg n=nlg 4 =n 2 (because algb = blga) l

Example (cont)

The Master method Used to solve equations of the form T(n) = a. T(n/b) + f(n) where a 1, b > 1, and f(n) is an asymptotically nonnegative function. Note: Version more general than one in text l

Master theorem • More general version than book

Master theorem • A different version of previous slide

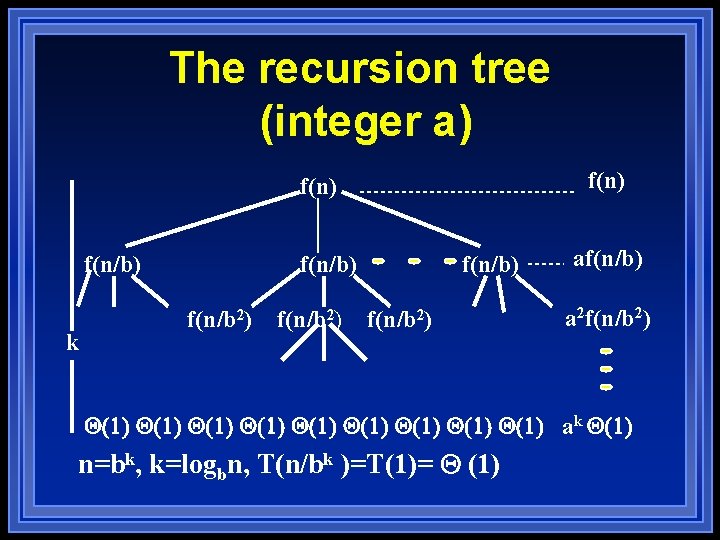
The recursion tree (integer a) f(n) f(n/b) k f(n/b) f(n/b 2) af(n/b) a 2 f(n/b 2) Q(1) Q(1) Q(1) ak Q(1) n=bk, k=logbn, T(n/bk )=T(1)= Q (1)

The Master method Let n=bk and k=logbn. l The number of leaves in the recursion tree is alog n = nlog a. l b b

Master method examples T(n) = 2 T(n/2) + Q(n) l a = b =2 l f(n)= Q(n) l nlog 2 = n, l Q(n)/n = Q(1) = Q(lg 0 n) l Case 2 and T(n)= Q(nlgn) l 2

Master method examples T(n) = 7 T(n/2) + Q(n 2). l a =7, b = 2 l nlog a = nlog 7 l Q(n 2)/nlog 7 = Q(n 2 -lg 7) = Q(n-0. 8) l Case 1 and T(n) = Q(nlog 7) l b 2 2 2

Master method examples l T(n) = T(n/2) + Q(1) Since nlog 1 = n 0 = 1, Q(1)/1 = Q(log 0 n), we are dealing with Case 2 and T(n) = Q(log n) 2

Master method examples l l T(n) = 4 T(n/2) + n 3 Since n 3/nlg 4 = n, we are dealing with Case 3. Is af(n/b) <= cf(n) for some c<1 and all sufficiently large n? yes 4(n/2)3 =n 3/2 so c=1/2 So T(n) = Q(n 3) The master method does not solve all recurrences of the given form.

Master method fails l T(n) = 4 T(n/2) + n 2/lgn (n 2/lgn)/n 2 = 1/lgn and no case applies

Master method fails l The solution is T(n) = Q(n 2 lglgn) and can be verified by the substitution method.

The Three Cases

Case 1: nlog a is polynomially larger than f(n). b f(n)= O(nlog a-e), or l f(n)/nlog a = O(n-e) , or l nlog a/ f(n) = W(ne) for some constant e > 0 l We bound the sum within the Onotation by factoring the terms, the remaining sum is an increasing geometric series l b b b

g(n) for case 1

g(n) for Case 1

g(n) for Case 1

Case 1: nlog a is polynomially larger than f(n). b l Total weight is (constant *number leaves).

Case 2: nlog a and f(n) are within a b polylogarithmic factor. f(n)/ nlog a = Q(lgkn) for some constant k 0. l T(n) = Q(nlog a) + Q(nlog a lgk+1 n)= = Q(nlog a lgk+1 n) l b b

g(n) for Case 2

g(n) for Case 2

g(n) for Case 2

g(n) for Case 2

Case 3: nlogba is polynomially smaller than f(n)/ nlog a = W (ne) for some constant e > 0. l Total weight is (constant times weight of root). l T(n) = Q(nlog a) + Q(f(n))= Q(f(n)) l b b

Case 3: nlogba is polynomially smaller than f(n). We will show that 1. g(n)= W(f(n)), and 2. g(n)=O(f(n)) and therefore g(n)= Q(f(n)) l

Case 3: nlogba is polynomially smaller than f(n). 1. We know that a 1 and that f(n) 0 for all large enough n l So all terms of g(n) are nonnegative for large enough n. l The first term of g(n) is f(n), so g(n) for all large enough n and g(n)=W(f(n))

Case 3

Case 3

Next class l Quicksort