CS 558 COMPUTER VISION Lecture VI Corner and

CS 558 COMPUTER VISION Lecture VI: Corner and Blob Detection Slides adapted from S. Lazebnik

OUTLINE Corner detection � Why detecting features? � Finding corners: basic idea and mathematics � Steps of Harris corner detector Blob detection � Scale selection � Laplacian of Gaussian (Lo. G) detector � Difference of Gaussian (Do. G) detector � Affine co-variant region

OUTLINE Corner detection � Why detecting features? � Finding corners: basic idea and mathematics � Steps of Harris corner detector Blob detection � Scale selection � Laplacian of Gaussian (Lo. G) detector � Difference of Gaussian (Do. G) detector � Affine co-variant region

FEATURE EXTRACTION: CORNERS 9300 Harris Corners Pkwy, Charlotte, NC

OUTLINE Corner detection � Why detecting features? � Finding corners: basic idea and mathematics � Steps of Harris corner detector Blob detection � Scale selection � Laplacian of Gaussian (Lo. G) detector � Difference of Gaussian (Do. G) detector � Affine co-variant region

WHY EXTRACT FEATURES? • Motivation: panorama stitching � We have two images – how do we combine them?

WHY EXTRACT FEATURES? • Motivation: panorama stitching � We have two images – how do we combine them? Step 1: extract features Step 2: match features

WHY EXTRACT FEATURES? • Motivation: panorama stitching � We have two images – how do we combine them? Step 1: extract features Step 2: match features Step 3: align images

CHARACTERISTICS OF GOOD FEATURES • Repeatability � • Saliency � • Each feature is distinctive Compactness and efficiency � • The same feature can be found in several images despite geometric and photometric transformations Many fewer features than image pixels Locality � A feature occupies a relatively small area of the image; robust to clutter and occlusion

APPLICATIONS Feature points are used for: � Image alignment � 3 D reconstruction � Motion tracking � Robot navigation � Indexing and database retrieval � Object recognition

OUTLINE Corner detection � Why detecting features? � Finding corners: basic idea and mathematics � Steps of Harris corner detector Blob detection � Scale selection � Laplacian of Gaussian (Lo. G) detector � Difference of Gaussian (Do. G) detector � Affine co-variant region

FINDING CORNERS • • Key property: in the region around a corner, image gradient has two or more dominant directions Corners are repeatable and distinctive C. Harris and M. Stephens. "A Combined Corner and Edge Detector. “ Proceedings of the 4 th Alvey Vision Conference: pages 147— 151, 1988.

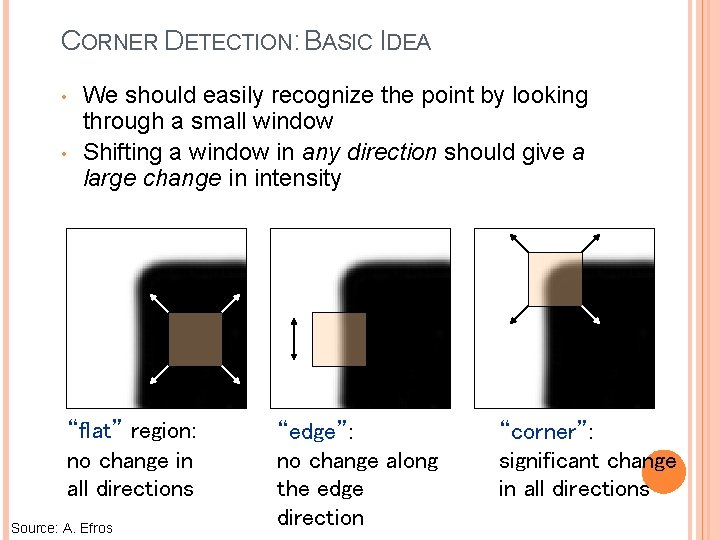
CORNER DETECTION: BASIC IDEA • • We should easily recognize the point by looking through a small window Shifting a window in any direction should give a large change in intensity “flat” region: no change in all directions Source: A. Efros “edge”: no change along the edge direction “corner”: significant change in all directions

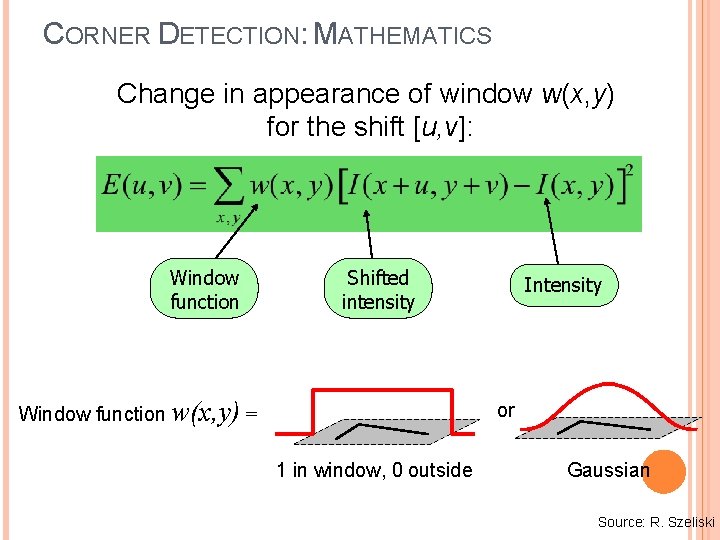
CORNER DETECTION: MATHEMATICS Change in appearance of window w(x, y) for the shift [u, v]: I(x, y) E(u, v) E(3, 2) w(x, y)

CORNER DETECTION: MATHEMATICS Change in appearance of window w(x, y) for the shift [u, v]: I(x, y) E(u, v) E(0, 0) w(x, y)

CORNER DETECTION: MATHEMATICS Change in appearance of window w(x, y) for the shift [u, v]: Window function Shifted intensity Window function w(x, y) = Intensity or 1 in window, 0 outside Gaussian Source: R. Szeliski

CORNER DETECTION: MATHEMATICS Change in appearance of window w(x, y) for the shift [u, v]: We want to find out how this function behaves for small shifts E(u, v)

CORNER DETECTION: MATHEMATICS Change in appearance of window w(x, y) for the shift [u, v]: We want to find out how this function behaves for small shifts Local quadratic approximation of E(u, v) in the neighborhood of (0, 0) is given by the second-order Taylor expansion:

CORNER DETECTION: MATHEMATICS Second-order Taylor expansion of E(u, v) about (0, 0):

CORNER DETECTION: MATHEMATICS Second-order Taylor expansion of E(u, v) about (0, 0):

CORNER DETECTION: MATHEMATICS Second-order Taylor expansion of E(u, v) about (0, 0):

CORNER DETECTION: MATHEMATICS The quadratic approximation simplifies to where M is a second moment matrix computed from image derivatives: M

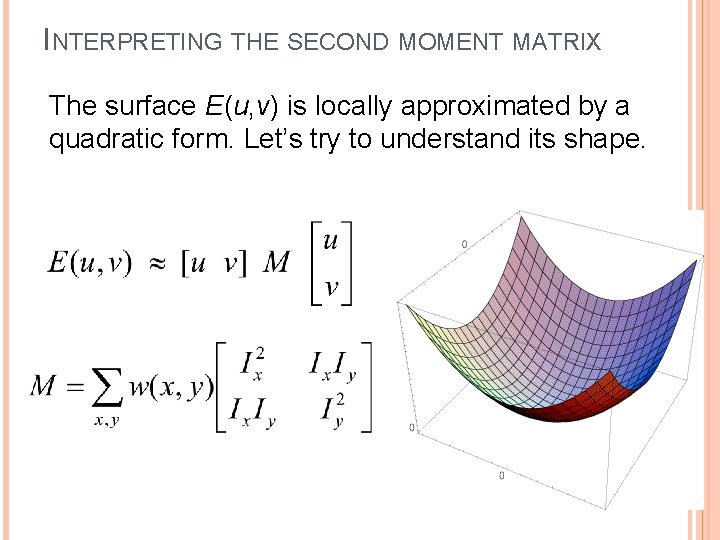
INTERPRETING THE SECOND MOMENT MATRIX The surface E(u, v) is locally approximated by a quadratic form. Let’s try to understand its shape.

INTERPRETING THE SECOND MOMENT MATRIX First, consider the axis-aligned case (gradients are either horizontal or vertical) If either λ is close to 0, then this is not a corner, so look for locations where both are large.

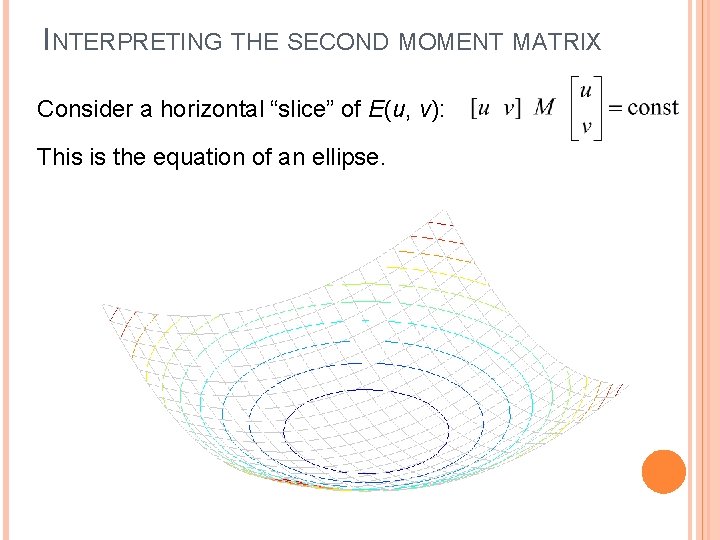
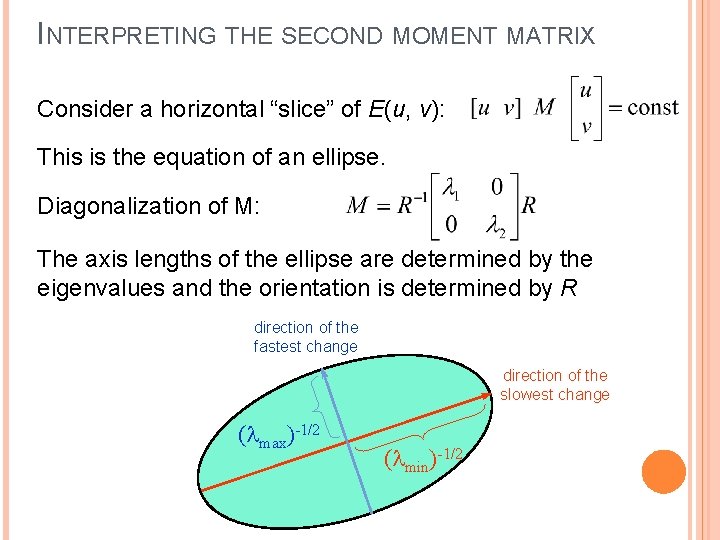
INTERPRETING THE SECOND MOMENT MATRIX Consider a horizontal “slice” of E(u, v): This is the equation of an ellipse.

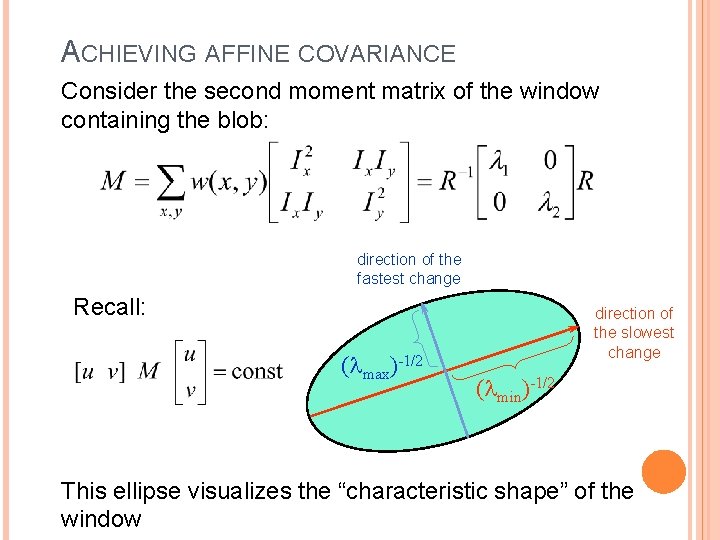
INTERPRETING THE SECOND MOMENT MATRIX Consider a horizontal “slice” of E(u, v): This is the equation of an ellipse. Diagonalization of M: The axis lengths of the ellipse are determined by the eigenvalues and the orientation is determined by R direction of the fastest change direction of the slowest change ( max)-1/2 ( min)-1/2

VISUALIZATION OF SECOND MOMENT MATRICES

VISUALIZATION OF SECOND MOMENT MATRICES

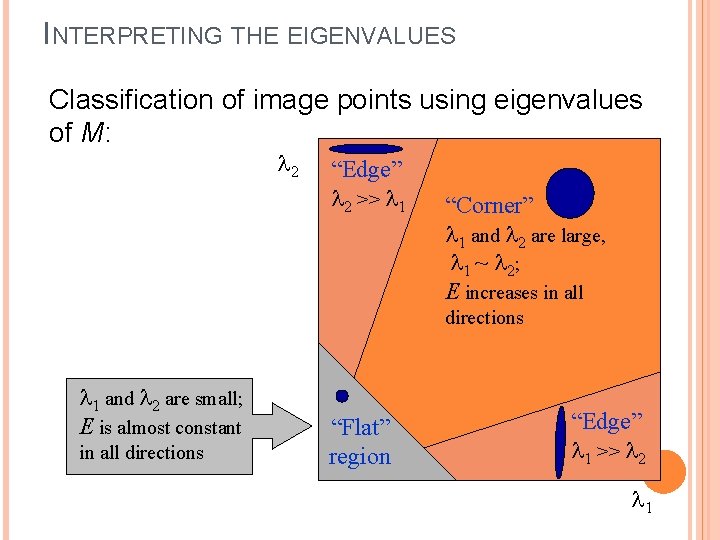
INTERPRETING THE EIGENVALUES Classification of image points using eigenvalues of M: 2 “Edge” 2 >> 1 “Corner” 1 and 2 are large, 1 ~ 2; E increases in all directions 1 and 2 are small; E is almost constant in all directions “Flat” region “Edge” 1 >> 2 1

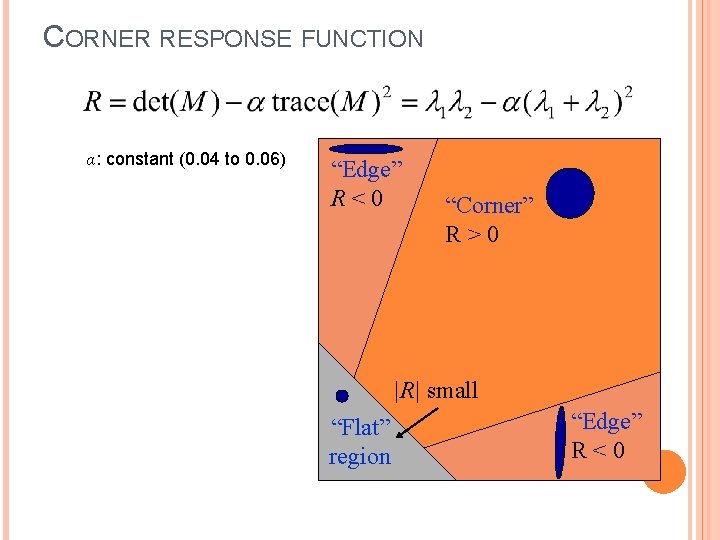
CORNER RESPONSE FUNCTION α: constant (0. 04 to 0. 06) “Edge” R<0 “Corner” R>0 |R| small “Flat” region “Edge” R<0

OUTLINE Corner detection � Why detecting features? � Finding corners: basic idea and mathematics � Steps of Harris corner detector Blob detection � Scale selection � Laplacian of Gaussian (Lo. G) detector � Difference of Gaussian (Do. G) detector � Affine co-variant region

HARRIS DETECTOR: STEPS 1. 2. 3. 4. 5. Compute Gaussian derivatives at each pixel Compute second moment matrix M in a Gaussian window around each pixel Compute corner response function R Threshold R Find local maxima of response function (nonmaximum suppression) C. Harris and M. Stephens. “A Combined Corner and Edge Detector. ” Proceedings of the 4 th Alvey Vision Conference: pages 147— 151, 1988.

HARRIS DETECTOR: STEPS

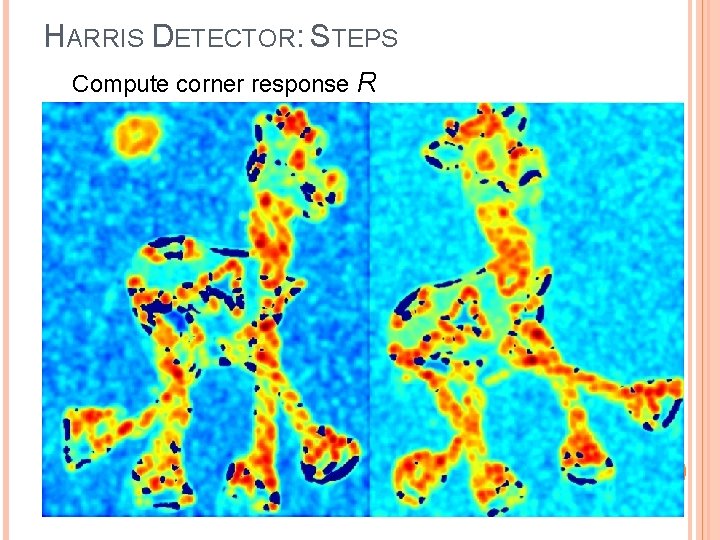
HARRIS DETECTOR: STEPS Compute corner response R

HARRIS DETECTOR: STEPS Find points with large corner response: R>threshold

HARRIS DETECTOR: STEPS Take only the points of local maxima of R

HARRIS DETECTOR: STEPS

INVARIANCE AND COVARIANCE • We want corner locations to be invariant to photometric transformations and covariant to geometric transformations � Invariance: image is transformed and corner locations do not change � Covariance: if we have two transformed versions of the same image, features should be detected in corresponding locations

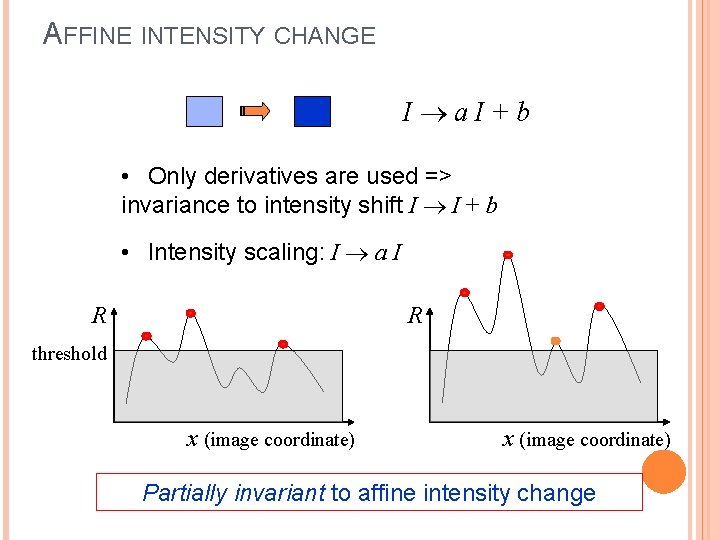
AFFINE INTENSITY CHANGE I a. I+b • Only derivatives are used => invariance to intensity shift I I + b • Intensity scaling: I a I R R threshold x (image coordinate) Partially invariant to affine intensity change

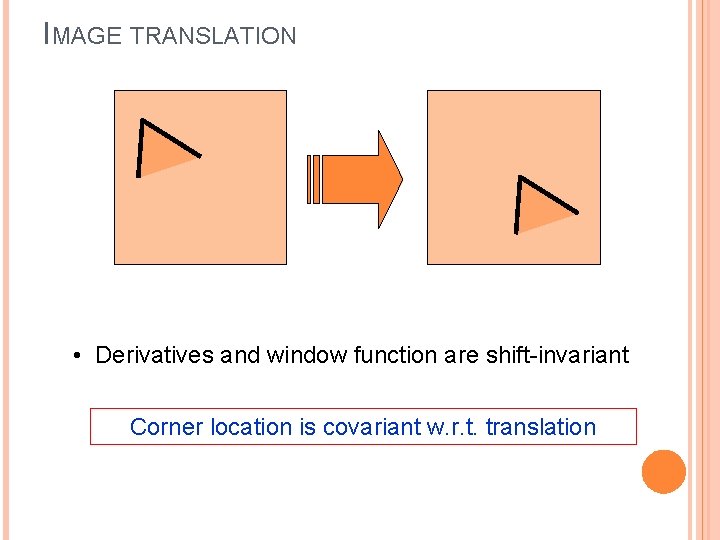
IMAGE TRANSLATION • Derivatives and window function are shift-invariant Corner location is covariant w. r. t. translation

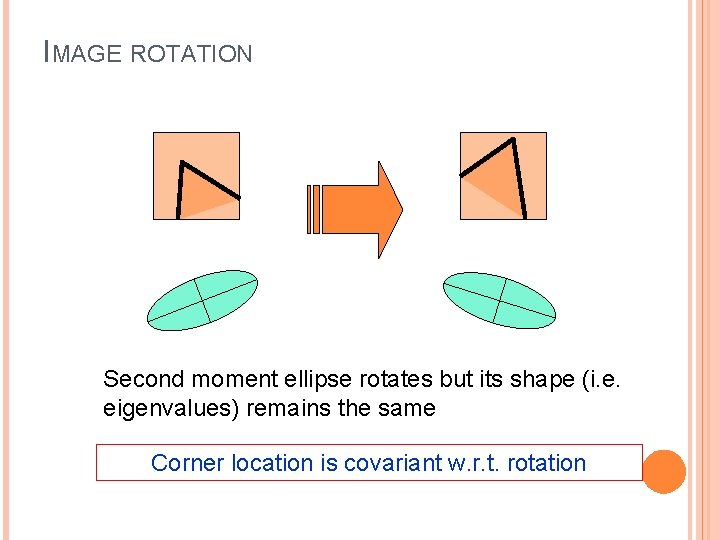
IMAGE ROTATION Second moment ellipse rotates but its shape (i. e. eigenvalues) remains the same Corner location is covariant w. r. t. rotation

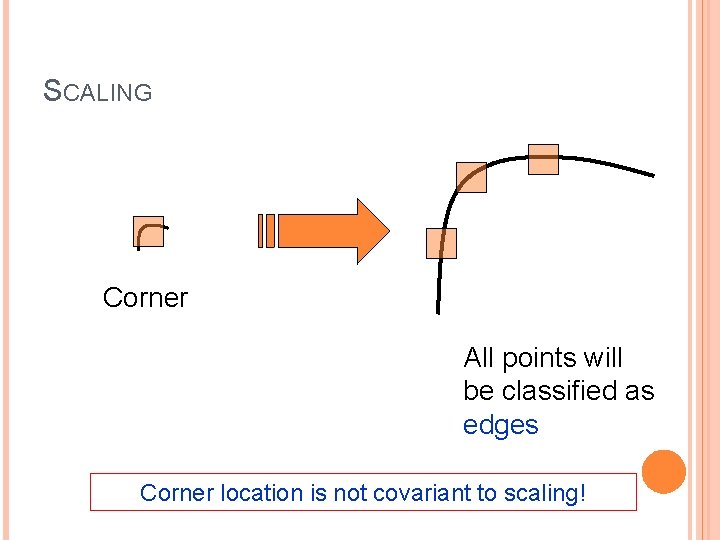
SCALING Corner All points will be classified as edges Corner location is not covariant to scaling!

OUTLINE Corner detection � Why detecting features? � Finding corners: basic idea and mathematics � Steps of Harris corner detector Blob detection � Scale selection � Laplacian of Gaussian (Lo. G) detector � Difference of Gaussian (Do. G) detector � Affine co-variant region

BLOB DETECTION

OUTLINE Corner detection � Why detecting features? � Finding corners: basic idea and mathematics � Steps of Harris corner detector Blob detection � Scale selection � Laplacian of Gaussian (Lo. G) detector � Difference of Gaussian (Do. G) detector � Affine co-variant region

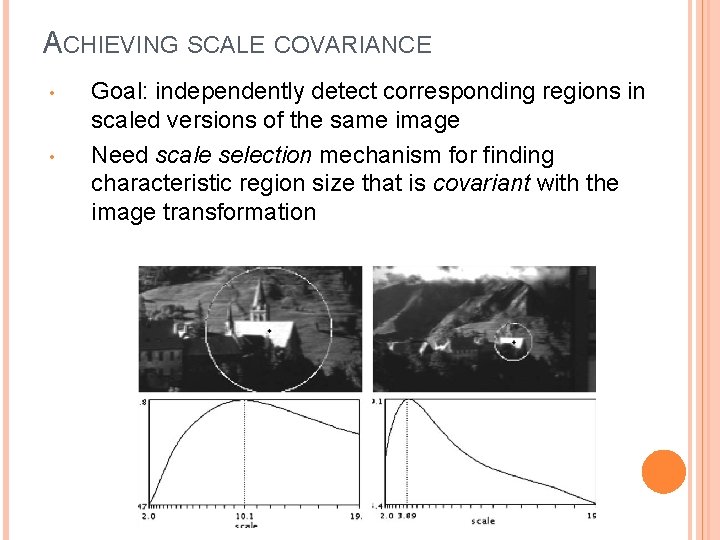
ACHIEVING SCALE COVARIANCE • • Goal: independently detect corresponding regions in scaled versions of the same image Need scale selection mechanism for finding characteristic region size that is covariant with the image transformation

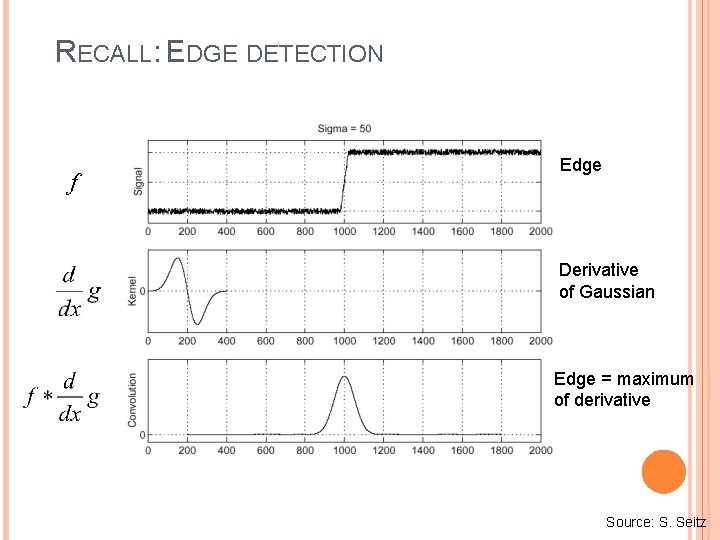
RECALL: EDGE DETECTION f Edge Derivative of Gaussian Edge = maximum of derivative Source: S. Seitz

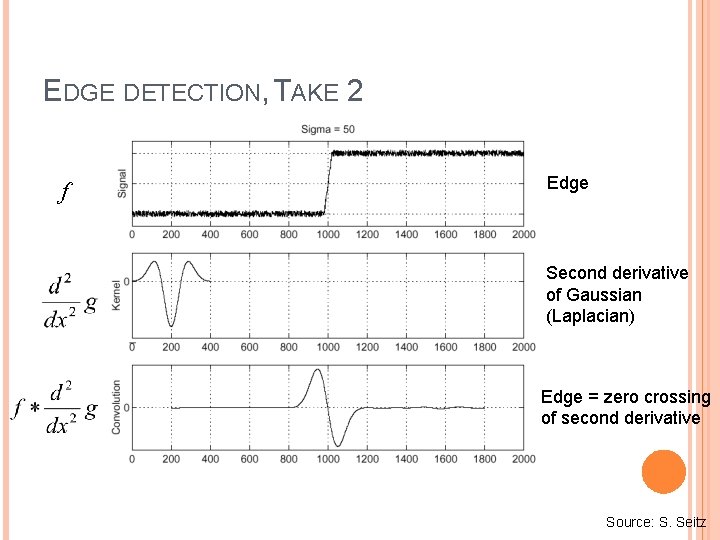
EDGE DETECTION, TAKE 2 f Edge Second derivative of Gaussian (Laplacian) Edge = zero crossing of second derivative Source: S. Seitz

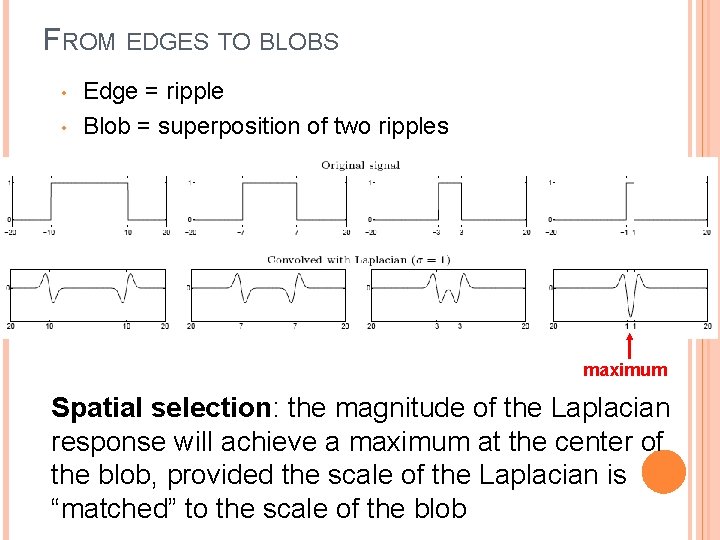
FROM EDGES TO BLOBS • • Edge = ripple Blob = superposition of two ripples maximum Spatial selection: the magnitude of the Laplacian response will achieve a maximum at the center of the blob, provided the scale of the Laplacian is “matched” to the scale of the blob

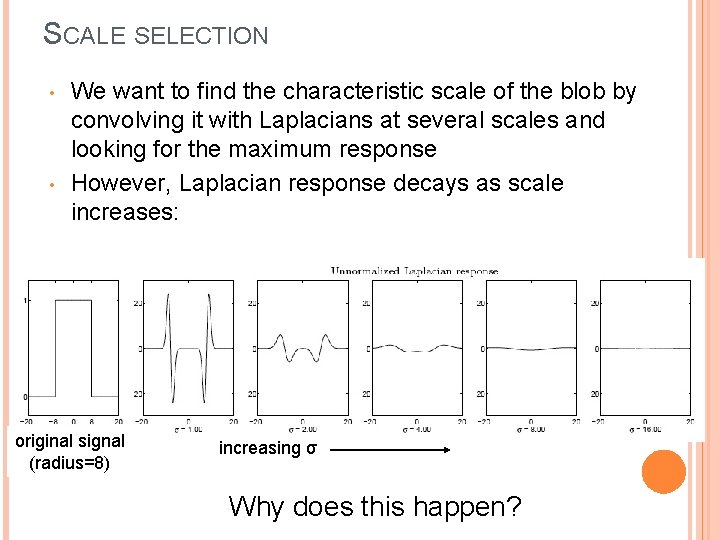
SCALE SELECTION • • We want to find the characteristic scale of the blob by convolving it with Laplacians at several scales and looking for the maximum response However, Laplacian response decays as scale increases: original signal (radius=8) increasing σ Why does this happen?

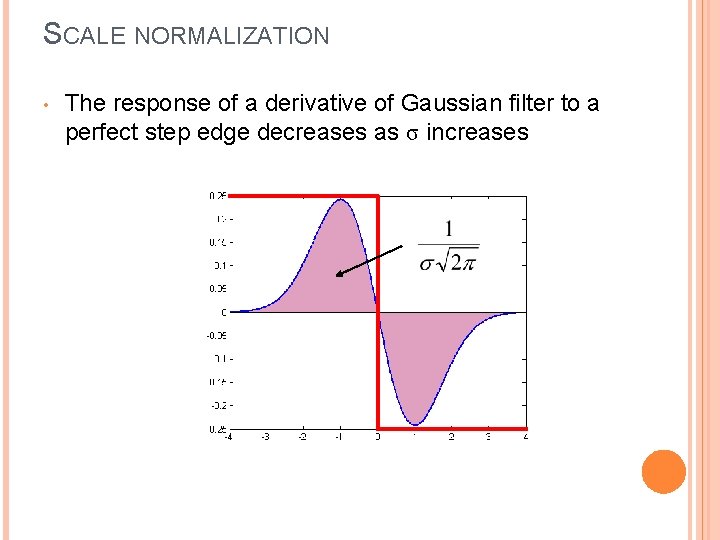
SCALE NORMALIZATION • The response of a derivative of Gaussian filter to a perfect step edge decreases as σ increases

SCALE NORMALIZATION • • • The response of a derivative of Gaussian filter to a perfect step edge decreases as σ increases To keep response the same (scale-invariant), must multiply Gaussian derivative by σ Laplacian is the second Gaussian derivative, so it must be multiplied by σ2

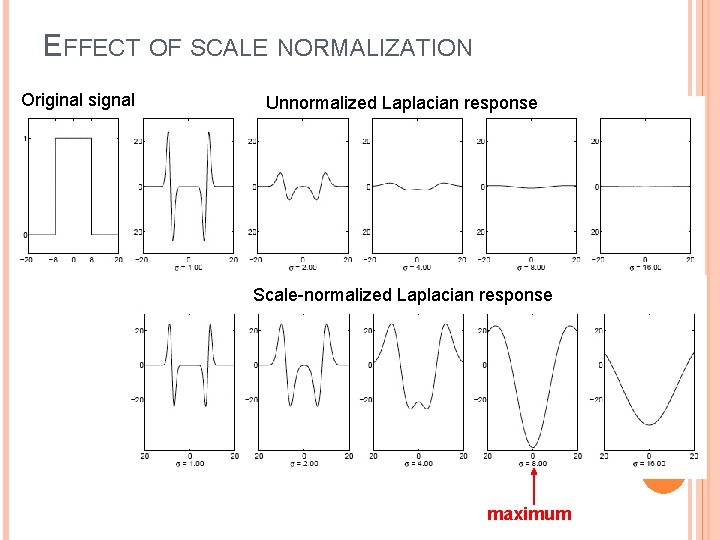
EFFECT OF SCALE NORMALIZATION Original signal Unnormalized Laplacian response Scale-normalized Laplacian response maximum

OUTLINE Corner detection � Why detecting features? � Finding corners: basic idea and mathematics � Steps of Harris corner detector Blob detection � Scale selection � Laplacian of Gaussian (Lo. G) detector � Difference of Gaussian (Do. G) detector � Affine co-variant region

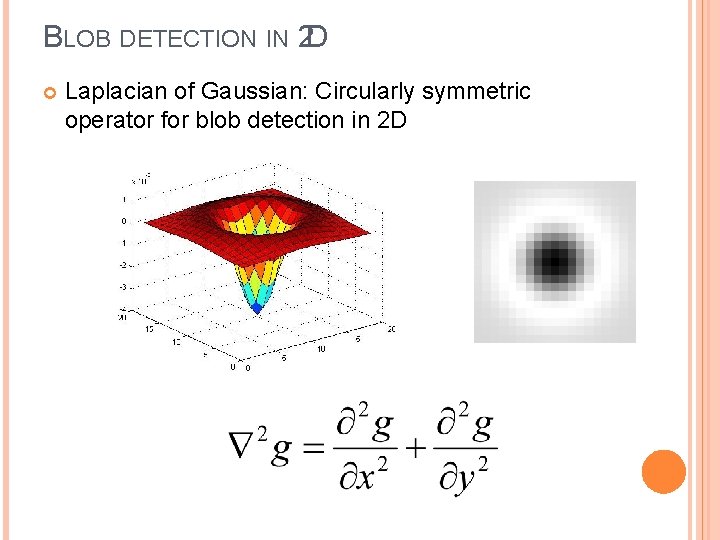
BLOB DETECTION IN 2 D Laplacian of Gaussian: Circularly symmetric operator for blob detection in 2 D

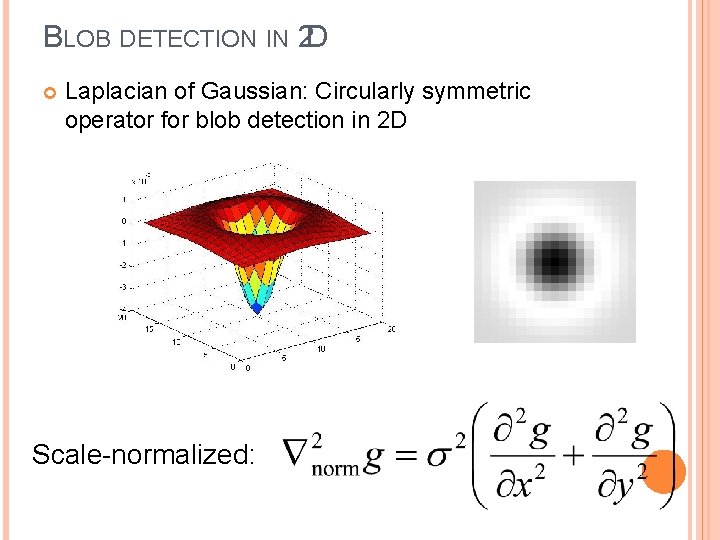
BLOB DETECTION IN 2 D Laplacian of Gaussian: Circularly symmetric operator for blob detection in 2 D Scale-normalized:

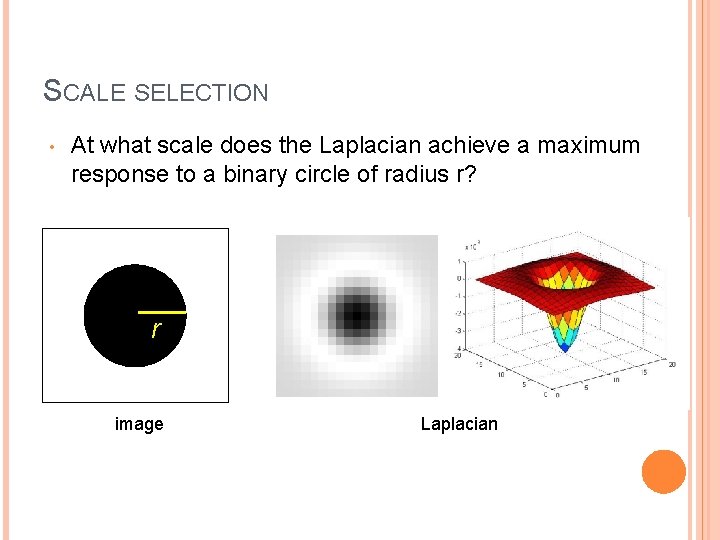
SCALE SELECTION • At what scale does the Laplacian achieve a maximum response to a binary circle of radius r? r image Laplacian

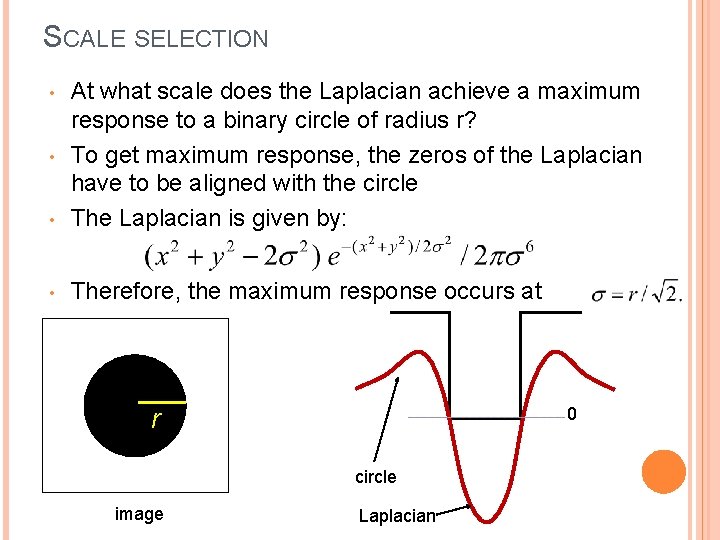
SCALE SELECTION • At what scale does the Laplacian achieve a maximum response to a binary circle of radius r? To get maximum response, the zeros of the Laplacian have to be aligned with the circle The Laplacian is given by: • Therefore, the maximum response occurs at • • r 0 circle image Laplacian

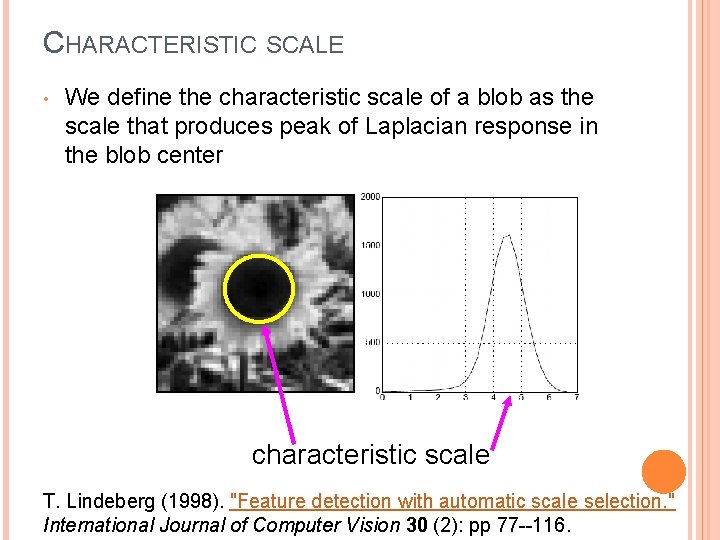
CHARACTERISTIC SCALE • We define the characteristic scale of a blob as the scale that produces peak of Laplacian response in the blob center characteristic scale T. Lindeberg (1998). "Feature detection with automatic scale selection. " International Journal of Computer Vision 30 (2): pp 77 --116.

SCALE-SPACE BLOB DETECTOR 1. Convolve image with scale-normalized Laplacian at several scales

SCALE-SPACE BLOB DETECTOR: EXAMPLE

SCALE-SPACE BLOB DETECTOR: EXAMPLE

SCALE-SPACE BLOB DETECTOR 1. 2. Convolve image with scale-normalized Laplacian at several scales Find maxima of squared Laplacian response in scale-space

SCALE-SPACE BLOB DETECTOR: EXAMPLE

OUTLINE Corner detection � Why detecting features? � Finding corners: basic idea and mathematics � Steps of Harris corner detector Blob detection � Scale selection � Laplacian of Gaussian (Lo. G) detector � Difference of Gaussian (Do. G) detector � Affine co-variant region

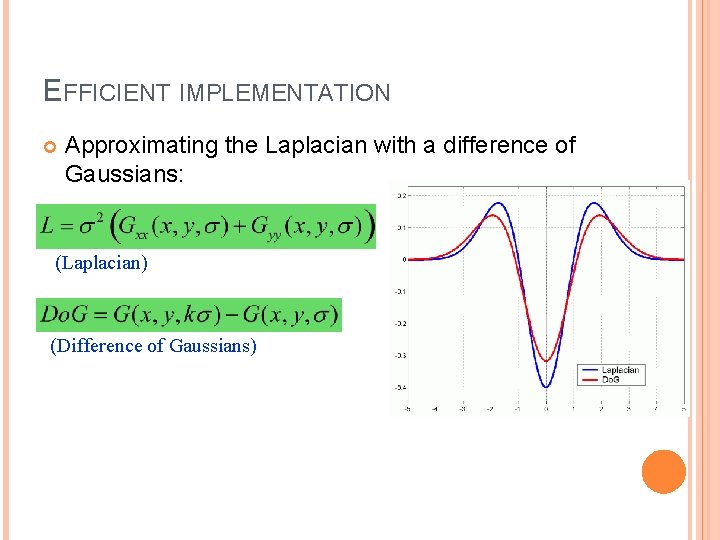
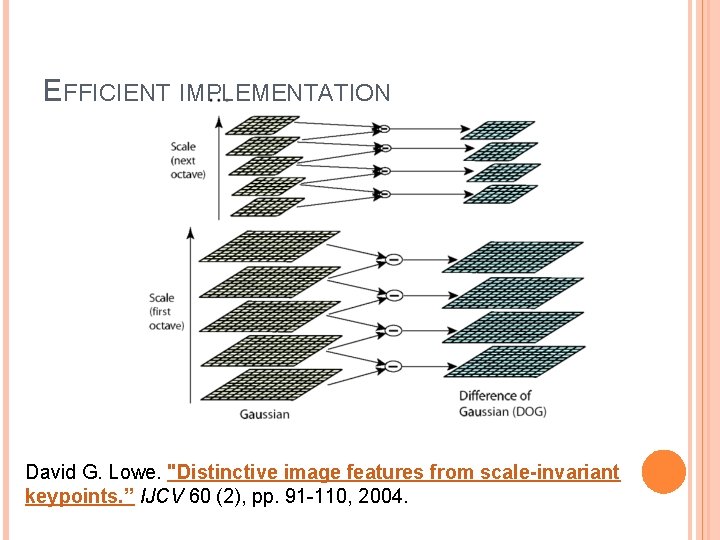
EFFICIENT IMPLEMENTATION Approximating the Laplacian with a difference of Gaussians: (Laplacian) (Difference of Gaussians)

EFFICIENT IMPLEMENTATION David G. Lowe. "Distinctive image features from scale-invariant keypoints. ” IJCV 60 (2), pp. 91 -110, 2004.

INVARIANCE AND COVARIANCE PROPERTIES • • • Laplacian (blob) response is invariant w. r. t. rotation and scaling Blob location and scale is covariant w. r. t. rotation and scaling What about intensity change?

OUTLINE Corner detection � Why detecting features? � Finding corners: basic idea and mathematics � Steps of Harris corner detector Blob detection � Scale selection � Laplacian of Gaussian (Lo. G) detector � Difference of Gaussian (Do. G) detector � Affine co-variant region

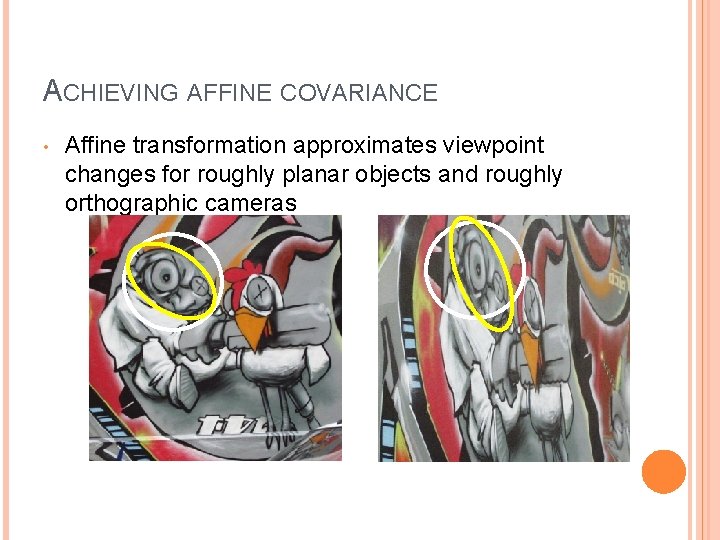
ACHIEVING AFFINE COVARIANCE • Affine transformation approximates viewpoint changes for roughly planar objects and roughly orthographic cameras

ACHIEVING AFFINE COVARIANCE Consider the second moment matrix of the window containing the blob: direction of the fastest change Recall: ( max)-1/2 direction of the slowest change ( min)-1/2 This ellipse visualizes the “characteristic shape” of the window

AFFINE ADAPTATION EXAMPLE Scale-invariant regions (blobs)

AFFINE ADAPTATION EXAMPLE Affine-adapted blobs

FROM COVARIANT DETECTION TO INVARIANT DESCRIPTION • • Geometrically transformed versions of the same neighborhood will give rise to regions that are related by the same transformation What to do if we want to compare the appearance of these image regions? � Normalization: transform these regions into same-size circles

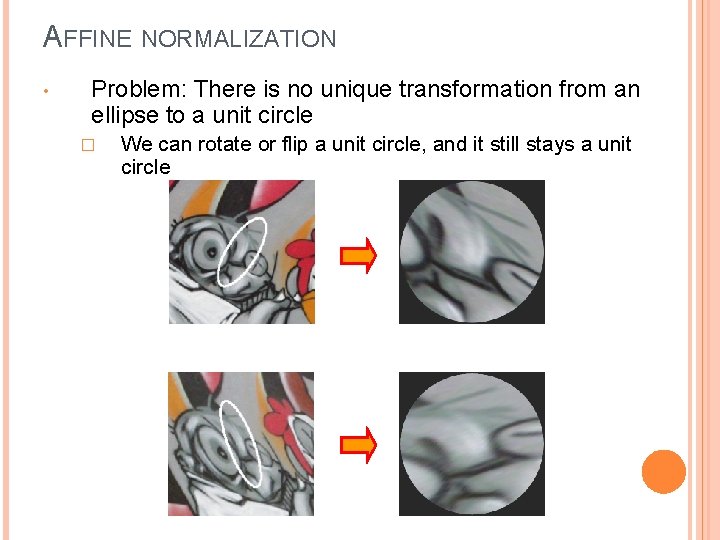
AFFINE NORMALIZATION • Problem: There is no unique transformation from an ellipse to a unit circle � We can rotate or flip a unit circle, and it still stays a unit circle

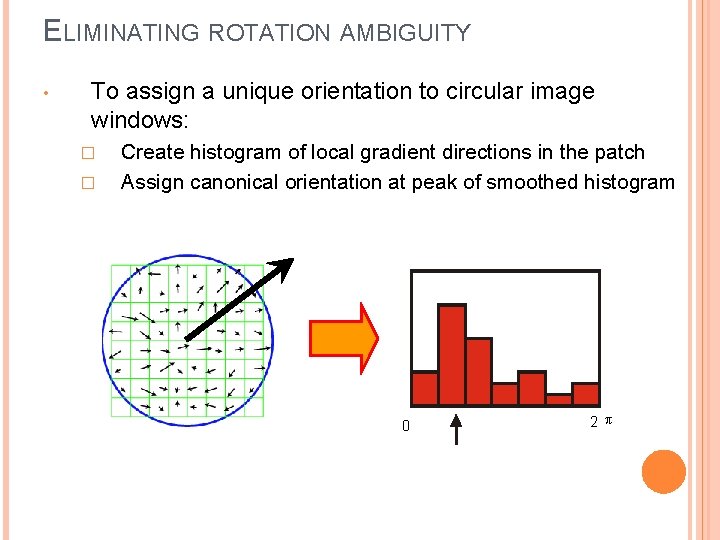
ELIMINATING ROTATION AMBIGUITY • To assign a unique orientation to circular image windows: � � Create histogram of local gradient directions in the patch Assign canonical orientation at peak of smoothed histogram 0 2 p

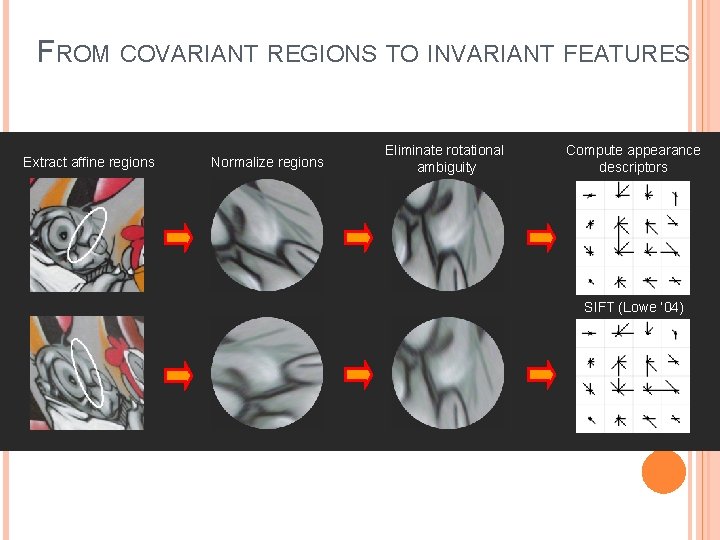
FROM COVARIANT REGIONS TO INVARIANT FEATURES Extract affine regions Normalize regions Eliminate rotational ambiguity Compute appearance descriptors SIFT (Lowe ’ 04)

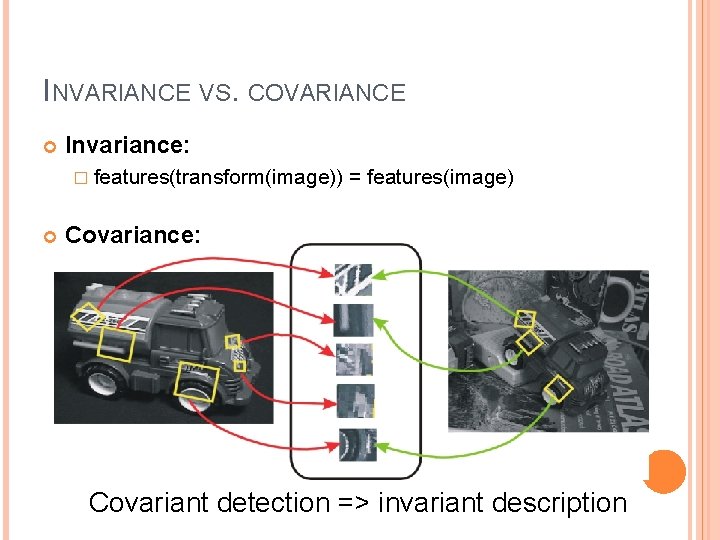
INVARIANCE VS. COVARIANCE Invariance: � features(transform(image)) = features(image) Covariance: � features(transform(image)) = transform(features(image)) Covariant detection => invariant description