CS 5263 Bioinformatics Lecture 5 Affine Gap Penalties

CS 5263 Bioinformatics Lecture 5: Affine Gap Penalties

Last lecture • Local Sequence Alignment • Bounded Dynamic Programming • Linear Space Sequence Alignment

The Smith-Waterman algorithm Initialization: F(0, j) = F(i, 0) = 0 0 F(i – 1, j) – d Iteration: F(i, j) = max F(i, j – 1) – d F(i – 1, j – 1) + (xi, yj)

The Smith-Waterman algorithm Termination: 1. If we want the best local alignment… FOPT = maxi, j F(i, j) 2. If we want all local alignments scoring > t For all i, j find F(i, j) > t, and trace back

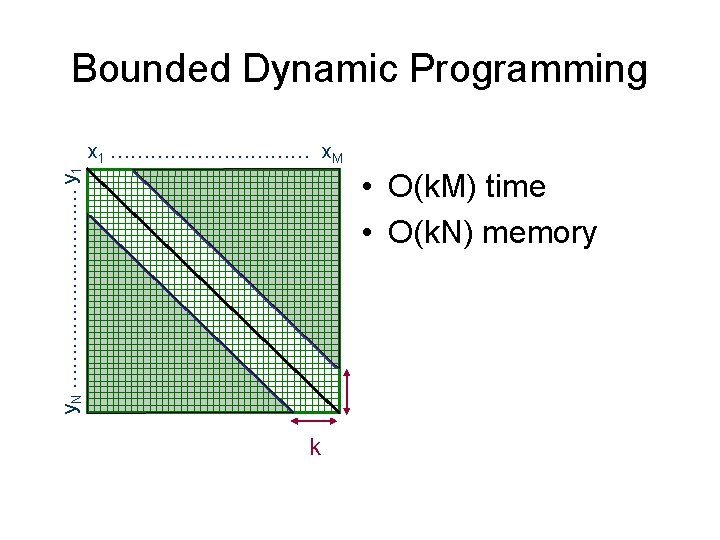
Bounded Dynamic Programming y. N …………… y 1 x 1 …………… x. M • O(k. M) time • O(k. N) memory k

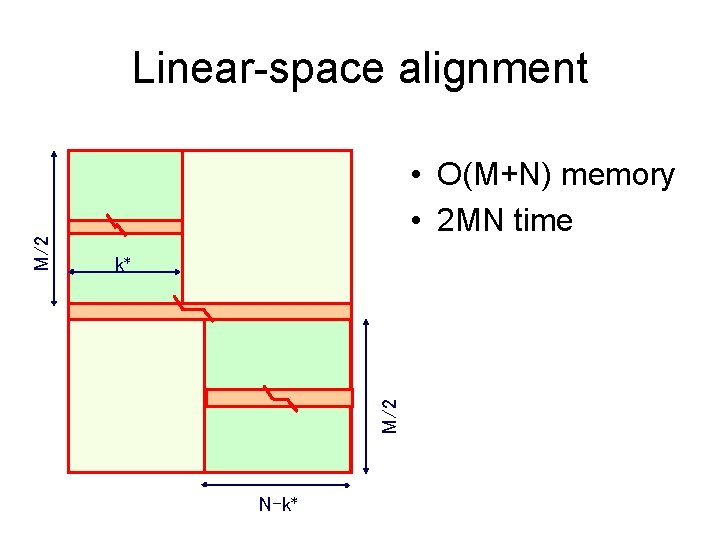
• O(M+N) memory • 2 MN time k* M/2 Linear-space alignment N-k*

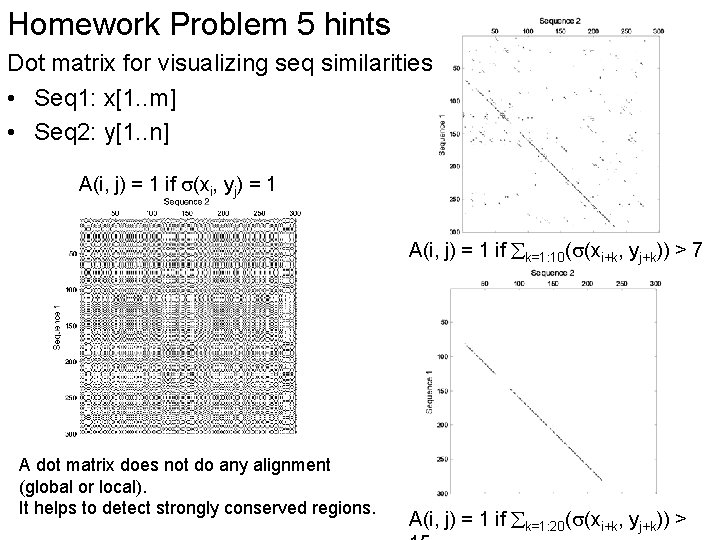
Homework Problem 5 hints Dot matrix for visualizing seq similarities • Seq 1: x[1. . m] • Seq 2: y[1. . n] A(i, j) = 1 if (xi, yj) = 1 A(i, j) = 1 if k=1: 10( (xi+k, yj+k)) > 7 A dot matrix does not do any alignment (global or local). It helps to detect strongly conserved regions. A(i, j) = 1 if k=1: 20( (xi+k, yj+k)) >

Seq 1 Seq 2

Today • How to model gaps more accurately? • Statistics of alignments – Where does (xi, yj) come from? – Are two aligned sequences actually related? – not today

What’s a better alignment? GACGCCGAACG ||||| GACGC---ACG GACGCCGAACG |||| | | || GACG-C-A-CG Score = 8 x m – 3 x d However, gaps usually occur in bunches. - During evolution, chunks of DNA may be lost entirely - Aligning genomic sequences vs. c. DNAs (reverse complimentary to m. RNAs)

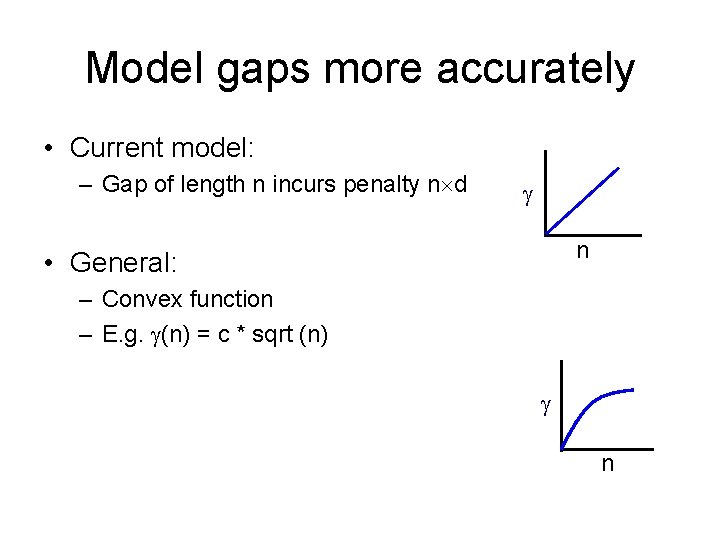
Model gaps more accurately • Current model: – Gap of length n incurs penalty n d n • General: – Convex function – E. g. (n) = c * sqrt (n) n

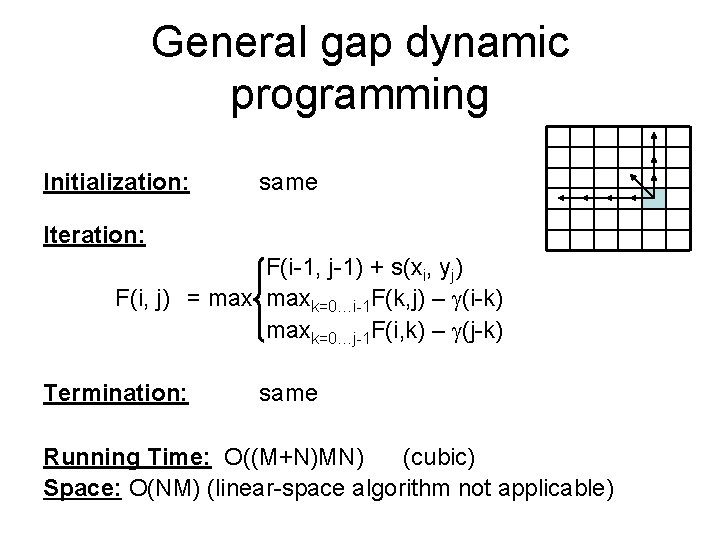
General gap dynamic programming Initialization: same Iteration: F(i-1, j-1) + s(xi, yj) F(i, j) = maxk=0…i-1 F(k, j) – (i-k) maxk=0…j-1 F(i, k) – (j-k) Termination: same Running Time: O((M+N)MN) (cubic) Space: O(NM) (linear-space algorithm not applicable)

Compromise: affine gaps (n) = d + (n – 1) e | | gap open extension Match: 2 Gap open: -5 Gap extension: -1 (n) e d GACGCCGAACG ||||| GACGC---ACG GACGCCGAACG |||| | | || GACG-C-A-CG 8 x 2 -5 -2 = 9 8 x 2 -3 x 5 = 1 We want to find the optimal alignment with affine gap penalty in • O(MN) time • O(MN) or better O(M+N) memory

Allowing affine gap penalties • Still three cases – xi aligned with yj – Xi aligns to a gap • Are we continuing a gap in x? (if no, start is more expensive) – Yj aligns to a gap • Are we continuing a gap in y? (if no, start is more expensive) • We can use a finite state machine to represent the three cases as three states – The machine has two heads, reading the chars on the two strings separately – At every step, each head reads 0 or 1 char from each sequence – Depending on what it reads, goes to a different state, and produces different scores

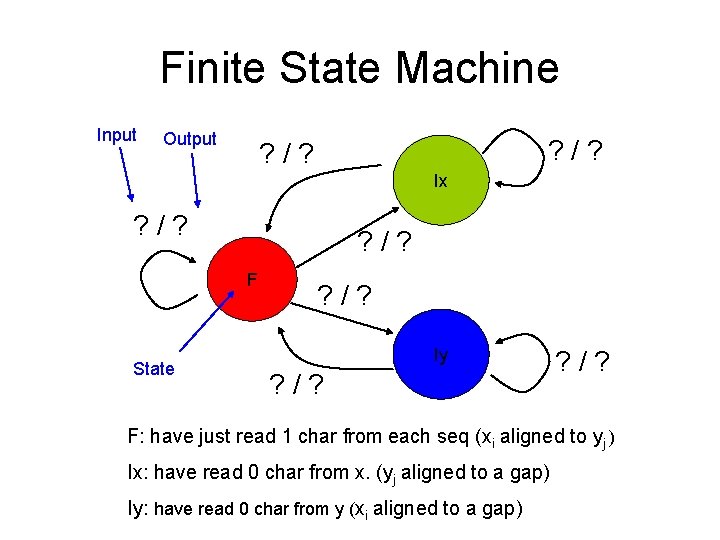
Finite State Machine Input Output ? /? Ix ? /? F State ? /? Iy ? /? F: have just read 1 char from each seq (xi aligned to yj ) Ix: have read 0 char from x. (yj aligned to a gap) Iy: have read 0 char from y (xi aligned to a gap)

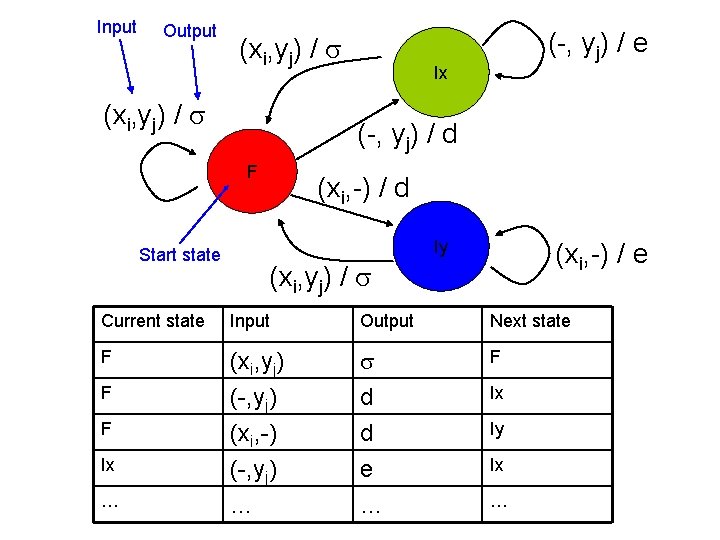
Input Output (xi, yj) / Ix (-, yj) / d F Start state (-, yj) / e (xi, -) / d Iy (xi, -) / e (xi, yj) / Current state Input Output Next state F (xi, yj) (-, yj) (xi, -) d d F (-, yj) … e … Ix F F Ix … Ix Iy …

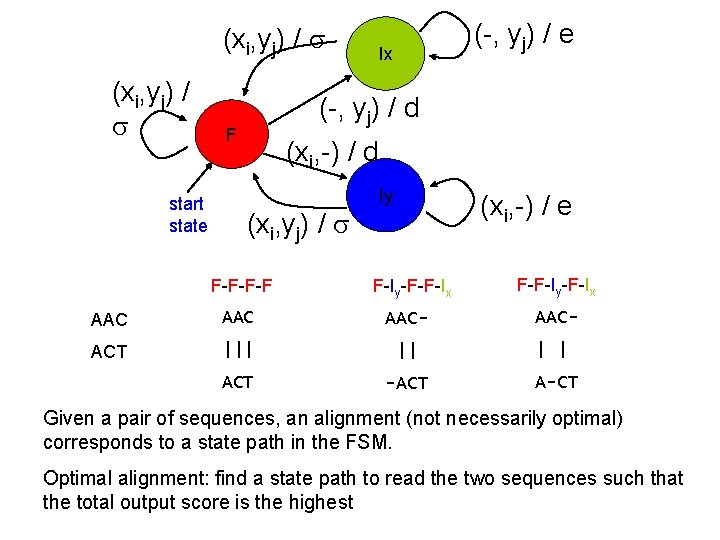
(xi, yj) / start state (-, yj) / e Ix (-, yj) / d F (xi, -) / d (xi, yj) / F-F-F-F Iy (xi, -) / e F-Iy-F-F-Ix AAC AAC- ACT ||| || ACT -ACT F-F-Iy-F-Ix AAC| | A-CT Given a pair of sequences, an alignment (not necessarily optimal) corresponds to a state path in the FSM. Optimal alignment: find a state path to read the two sequences such that the total output score is the highest

Dynamic programming • We encode this information in three different matrices • For each element (i, j) we use three variables – F(i, j): best alignment (score) of x 1. . xi & y 1. . yj if xi aligns to yj – Ix(i, j): best alignment of x 1. . xi & y 1. . yj if yj aligns to gap – Iy(i, j): best alignment of x 1. . xi & y 1. . yj if xi aligns to gap xi xi yj F(i, j) xi yj Ix(i, j) yj Iy(i, j)

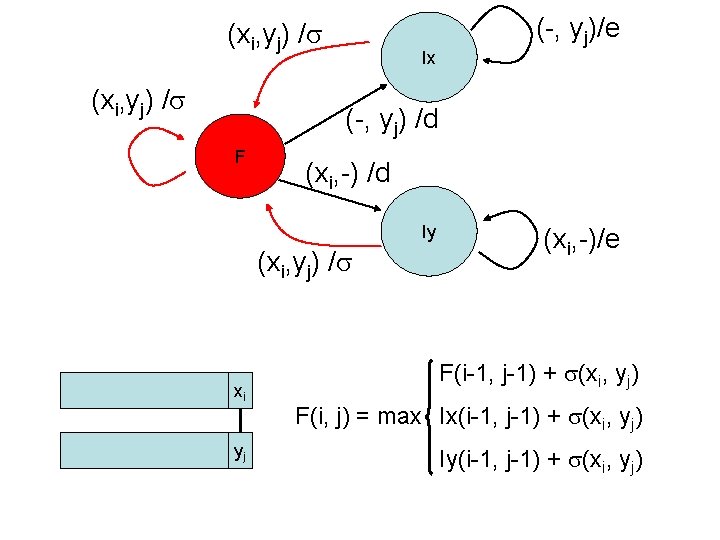
(xi, yj) / Ix (-, yj)/e (-, yj) /d F (xi, -) /d Iy (xi, yj) / xi yj (xi, -)/e F(i-1, j-1) + (xi, yj) F(i, j) = max Ix(i-1, j-1) + (xi, yj) Iy(i-1, j-1) + (xi, yj)

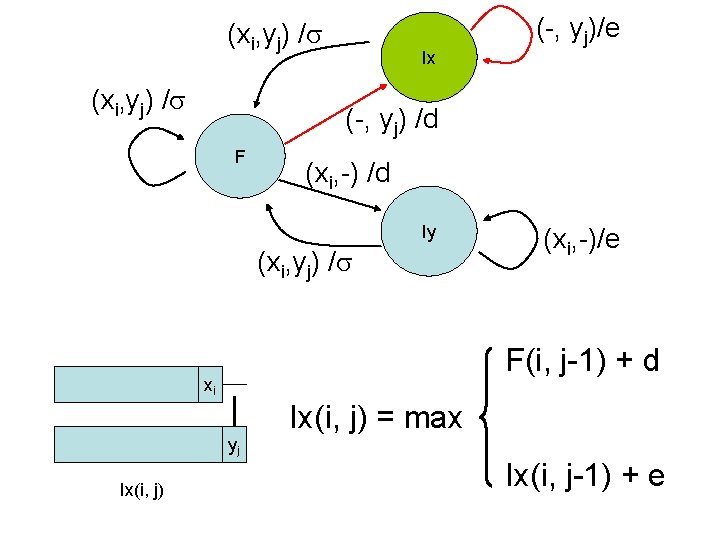
(xi, yj) / Ix (-, yj) /d F (xi, -) /d Iy (xi, yj) / (xi, -)/e F(i, j-1) + d xi yj Ix(i, j) (-, yj)/e Ix(i, j) = max Ix(i, j-1) + e

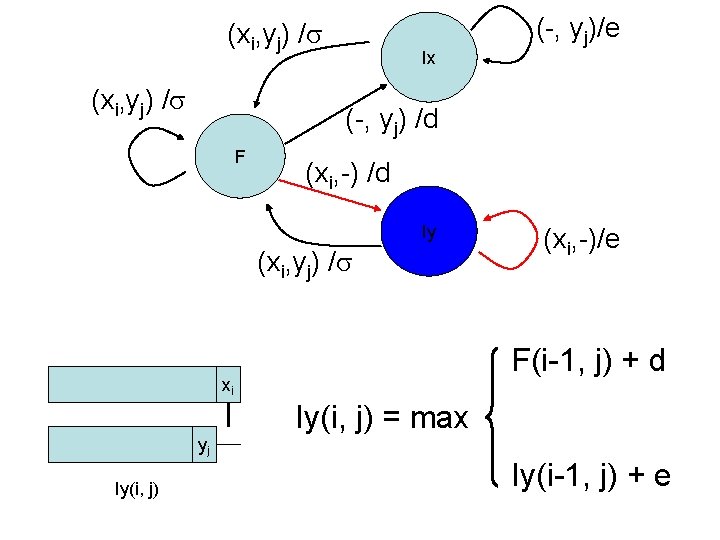
(xi, yj) / Ix (-, yj) /d F (xi, -) /d Iy (xi, yj) / yj (xi, -)/e F(i-1, j) + d xi Iy(i, j) (-, yj)/e Iy(i, j) = max Iy(i-1, j) + e

F(i – 1, j – 1) F(i, j) = (xi, yj) + max Ix(i – 1, j – 1) Iy(i – 1, j – 1) Ix(i, j) = max Iy(i, j) = max Continuing alignment Closing gaps in x Closing gaps in y F(i, j – 1) + d Opening a gap in x Ix(i, j – 1) + e Gap extension in x F(i – 1, j) + d Opening a gap in y Iy(i – 1, j) + e Gap extension in y

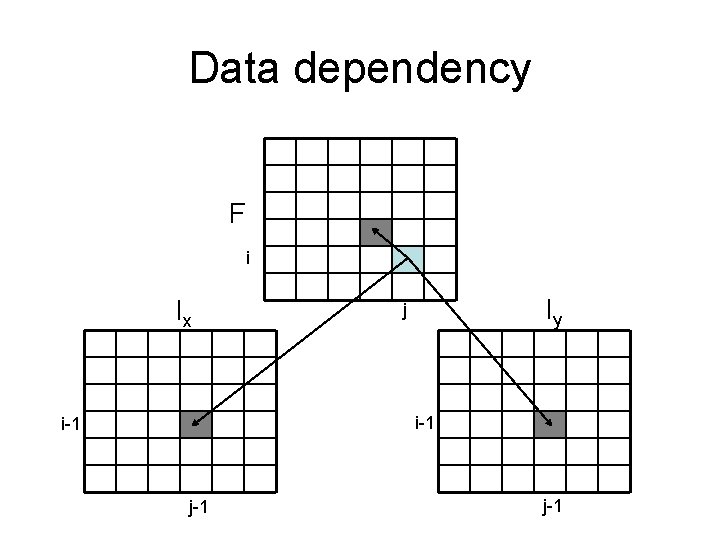
Data dependency F i Ix Iy j i-1 j-1

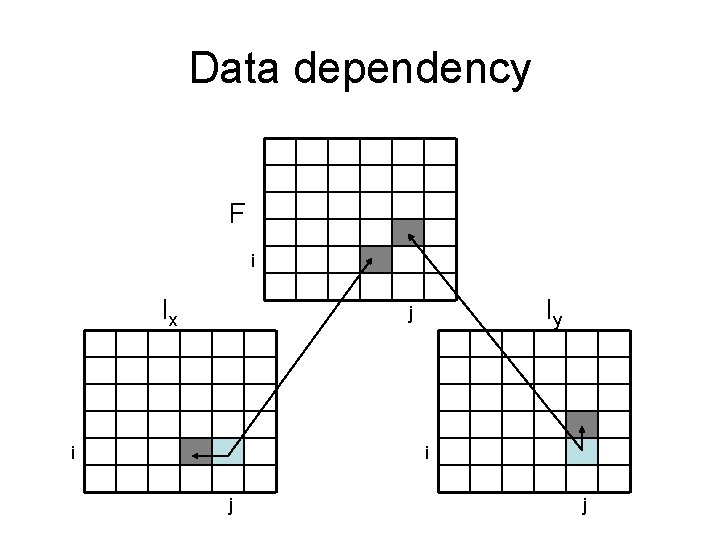
Data dependency F i Ix Iy j i i j j

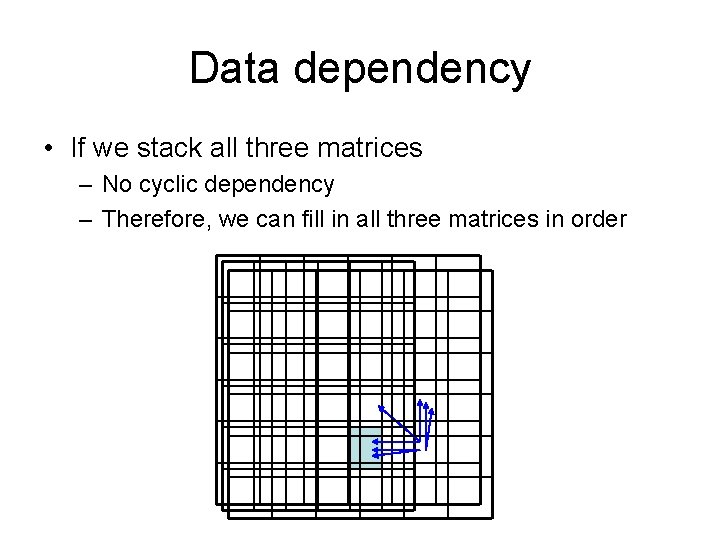
Data dependency • If we stack all three matrices – No cyclic dependency – Therefore, we can fill in all three matrices in order

Algorithm • for i = 1: m – for j = 1: n • Fill in F(i, j), Ix(i, j), Iy(i, j) – end • F(M, N) = max (F(M, N), Ix(M, N), Iy(M, N)) • Time: O(MN) • Space: O(MN) or O(N) when combine with the linear-space algorithm

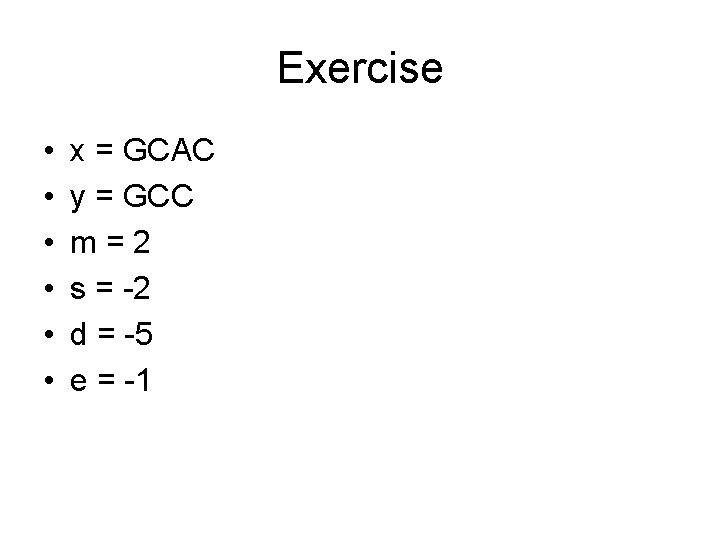
Exercise • • • x = GCAC y = GCC m=2 s = -2 d = -5 e = -1

y= G x= 0 - C - x= y= G C C - - - G -5 C -6 A -7 C -8 F: aligned on both y= G x = - -5 C -6 A C m=2 s = -2 d = -5 e = -1 Iy: Insertion on y C -7 F(i-1, j-1) - - Iy(i-1, j-1) (xi, yj) G - C - d Ix(i, j-1) e F(i, j) Iy(i, j) d - Ix: Insertion on x F(i-1, j) Ix(i-1, j-1) F(i, j-1) Iy(i-1, j) e Ix(i, j)

y= G x= 0 - G - C - 2 x= y= G C C - - G -5 C -6 A -7 C -8 F y= G x = - -5 C A C Iy C -6 C -7 F(i-1, j-1) G - m=2 s = -2 d = -5 e = -1 Iy(i-1, j-1) (xi, yj) = 2 - Ix(i-1, j-1) - F(i, j) - Ix

y= G x= 0 G - C - - 2 -7 C - x= y= G C C - - G -5 C -6 A -7 C -8 F y= G x = - -5 C A C Iy C -6 C -7 F(i-1, j-1) G - m=2 s = -2 d = -5 e = -1 Iy(i-1, j-1) (xi, yj) = -2 - Ix(i-1, j-1) - F(i, j) - Ix

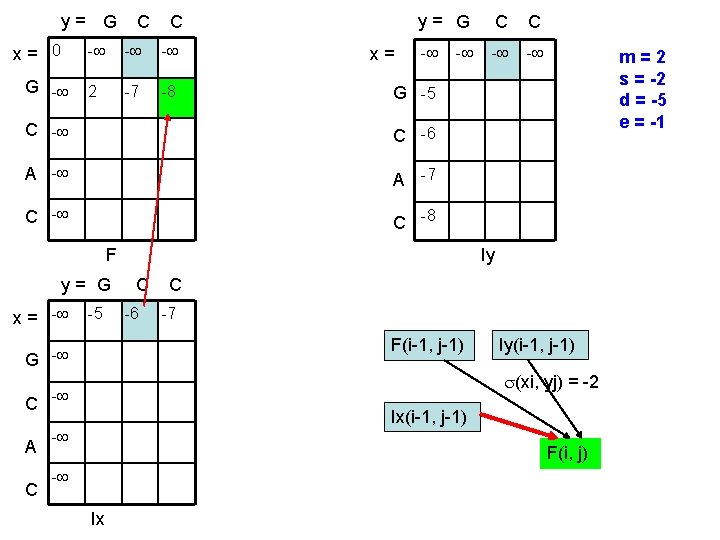
y= G x= 0 G - C C - - - 2 -7 -8 x= y= G C C - - G -5 C -6 A -7 C -8 F y= G x = - -5 C A C Iy C -6 C -7 F(i-1, j-1) G - m=2 s = -2 d = -5 e = -1 Iy(i-1, j-1) (xi, yj) = -2 - Ix(i-1, j-1) - F(i, j) - Ix

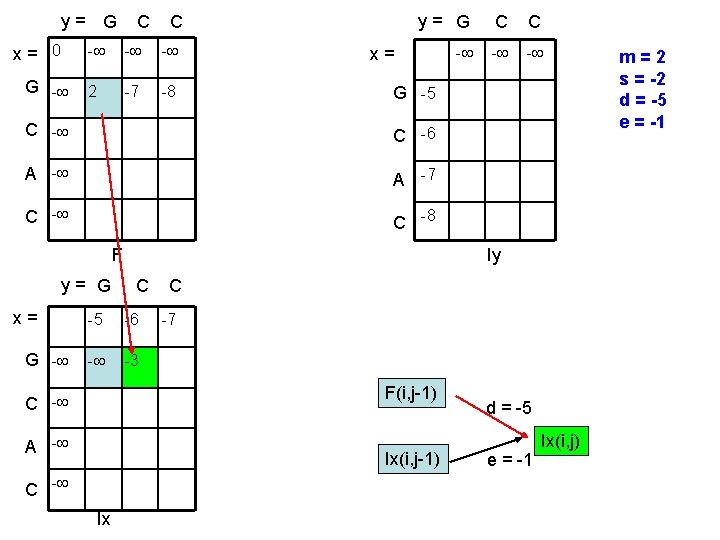
y= G x= 0 G - C C - - - 2 -7 -8 y= G C C - - - x= G -5 C -6 A -7 C -8 F y= G x= G - Iy C -5 -6 - -3 C -7 F(i, j-1) C - A - Ix(i, j-1) C - Ix d = -5 e = -1 Ix(i, j) m=2 s = -2 d = -5 e = -1

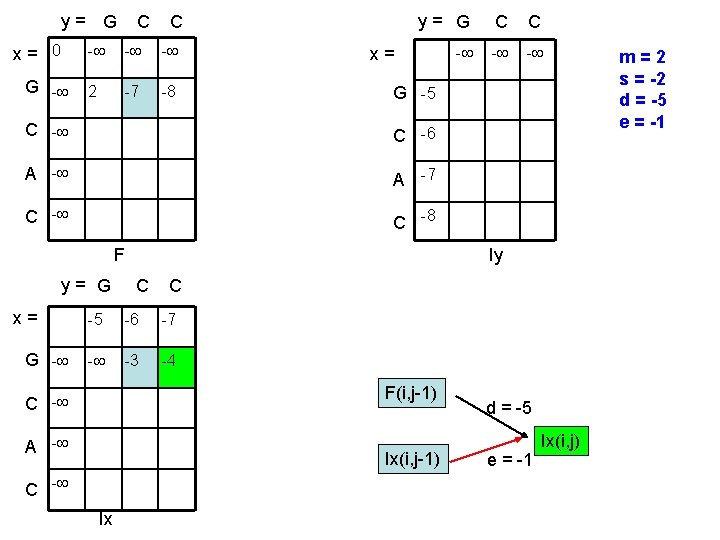
y= G x= 0 G - C C - - - 2 -7 -8 y= G C C - - - x= G -5 C -6 A -7 C -8 F y= G x= G - Iy C C -5 -6 -7 - -3 -4 F(i, j-1) C - A - Ix(i, j-1) C - Ix d = -5 e = -1 Ix(i, j) m=2 s = -2 d = -5 e = -1

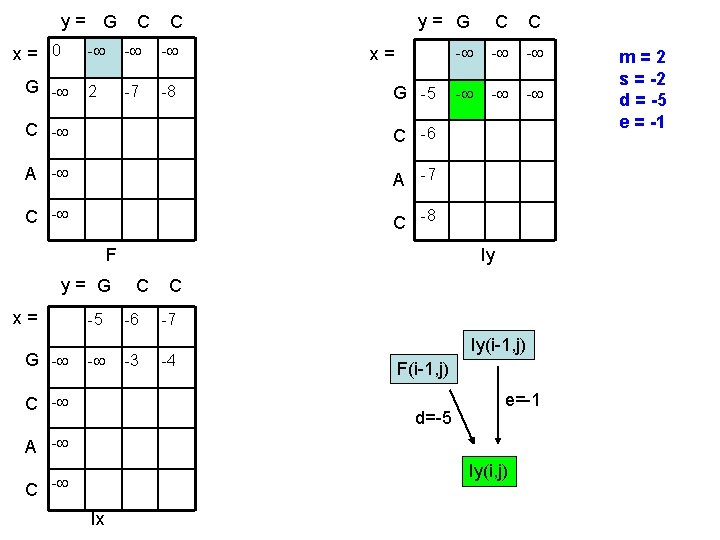
y= G x= 0 G - C C - - - 2 -7 -8 y= G C C - - - x= G -5 C -6 A -7 C -8 F y= G x= G - -5 - C - Iy C -6 -3 C -7 -4 Iy(i-1, j) F(i-1, j) d=-5 e=-1 A - Iy(i, j) C - Ix m=2 s = -2 d = -5 e = -1

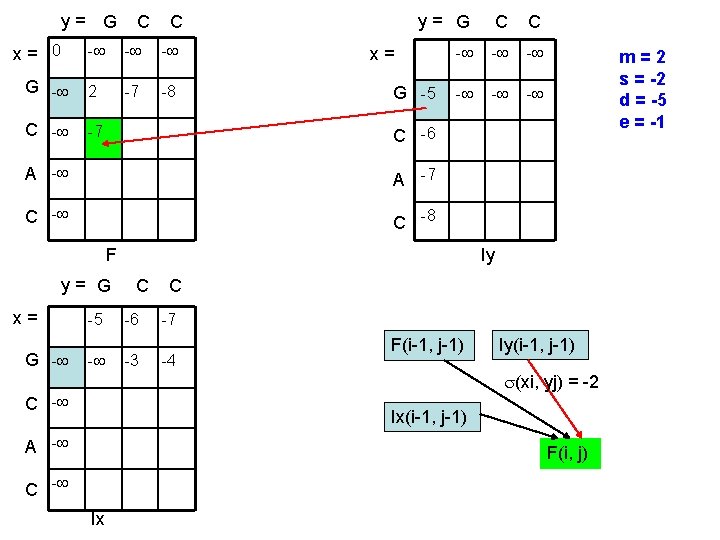
y= G x= 0 C C - - - G - 2 -7 -8 C - -7 y= G C C - - - x= G -5 C -6 A -7 C -8 F y= G x= G - -5 - m=2 s = -2 d = -5 e = -1 Iy C -6 -3 C -7 -4 F(i-1, j-1) Iy(i-1, j-1) (xi, yj) = -2 C - Ix(i-1, j-1) A - F(i, j) C - Ix

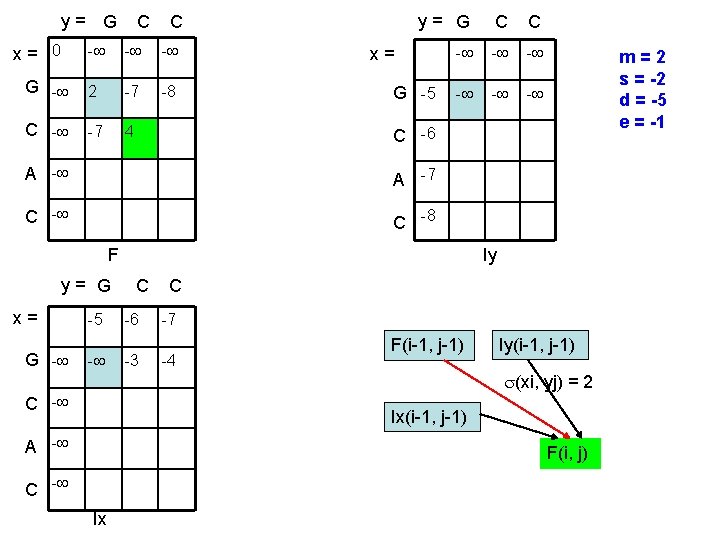
y= G x= 0 C C - - - G - 2 -7 -8 C - -7 4 y= G C C - - - x= G -5 C -6 A -7 C -8 F y= G x= G - -5 - m=2 s = -2 d = -5 e = -1 Iy C -6 -3 C -7 -4 F(i-1, j-1) Iy(i-1, j-1) (xi, yj) = 2 C - Ix(i-1, j-1) A - F(i, j) C - Ix

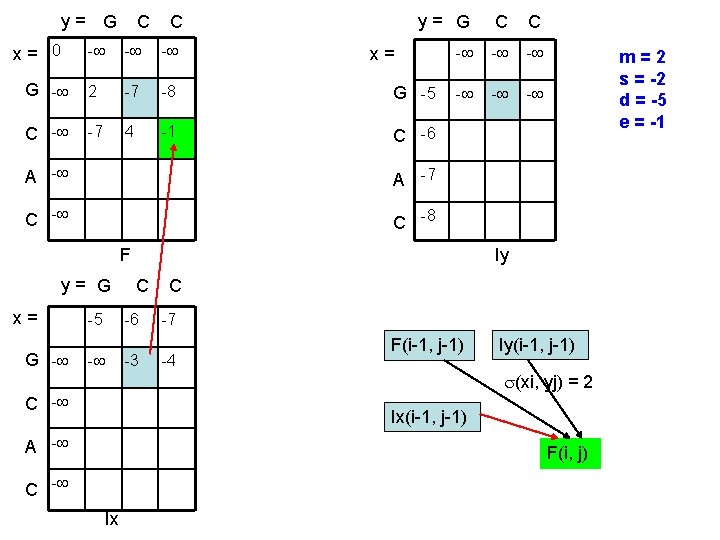
y= G x= 0 C C y= G C C - - - G - 2 -7 -8 G -5 C - -7 4 -1 C -6 x= A -7 C -8 F y= G x= G - -5 Iy C -6 - m=2 s = -2 d = -5 e = -1 -3 C -7 -4 F(i-1, j-1) Iy(i-1, j-1) (xi, yj) = 2 C - Ix(i-1, j-1) A - F(i, j) C - Ix

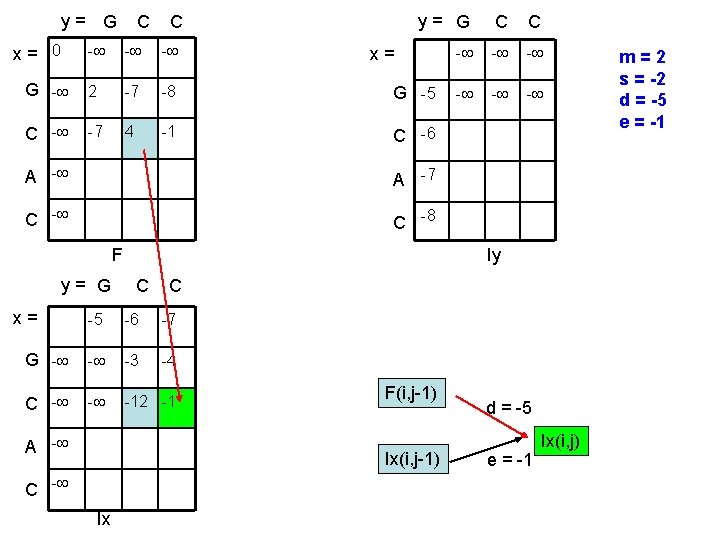
y= G x= 0 C C y= G C C - - - G - 2 -7 -8 G -5 C - -7 4 -1 C -6 x= A -7 C -8 F y= G x= Iy C C -5 -6 -7 G - - -3 -4 C - - -12 -1 A - F(i, j-1) Ix(i, j-1) C - Ix d = -5 e = -1 Ix(i, j) m=2 s = -2 d = -5 e = -1

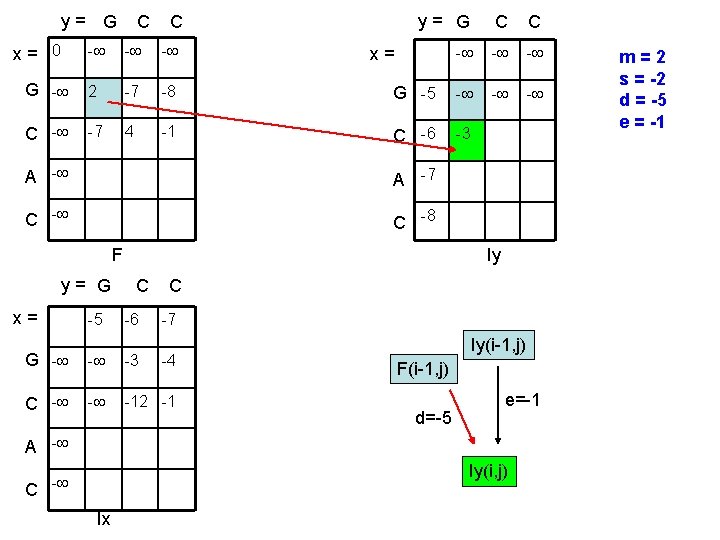
y= G x= 0 C C y= G C C - - G - 2 -7 -8 G -5 - C - -7 4 -1 C -6 -3 x= A -7 C -8 F y= G x= -5 Iy C -6 C -7 G - - -3 C - - -12 -1 -4 Iy(i-1, j) F(i-1, j) d=-5 e=-1 A - Iy(i, j) C - Ix m=2 s = -2 d = -5 e = -1

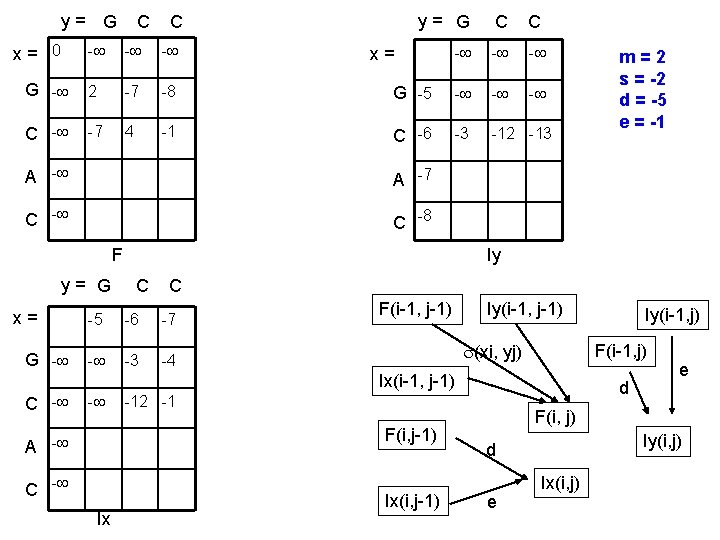
y= G x= 0 C C y= G C C - - G - 2 -7 -8 G -5 - - C - -7 4 -1 C -6 -3 -12 -13 x= A -7 C -8 F y= G x= G - Iy C C -5 -6 -7 - -3 -4 F(i-1, j-1) Iy(i-1, j-1) (xi, yj) - C - Ix d -12 -1 F(i, j-1) A - Ix(i, j-1) Iy(i-1, j) F(i-1, j) Ix(i-1, j-1) C - m=2 s = -2 d = -5 e = -1 e F(i, j) Iy(i, j) d e Ix(i, j)

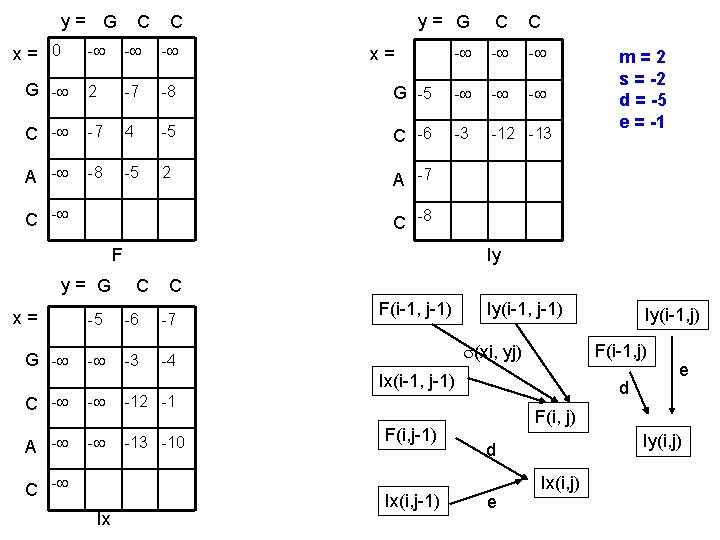
y= G x= 0 C C y= G C C - - G - 2 -7 -8 G -5 - - C - -7 4 -5 C -6 -3 -12 -13 A - -8 -5 2 A -7 C - x= C -8 F y= G x= G - m=2 s = -2 d = -5 e = -1 Iy C C -5 -6 -7 - -3 -4 F(i-1, j-1) Iy(i-1, j-1) (xi, yj) F(i-1, j) Ix(i-1, j-1) C - - -12 -1 A - - -13 -10 C - Ix F(i, j-1) Ix(i, j-1) Iy(i-1, j) d e F(i, j) Iy(i, j) d e Ix(i, j)

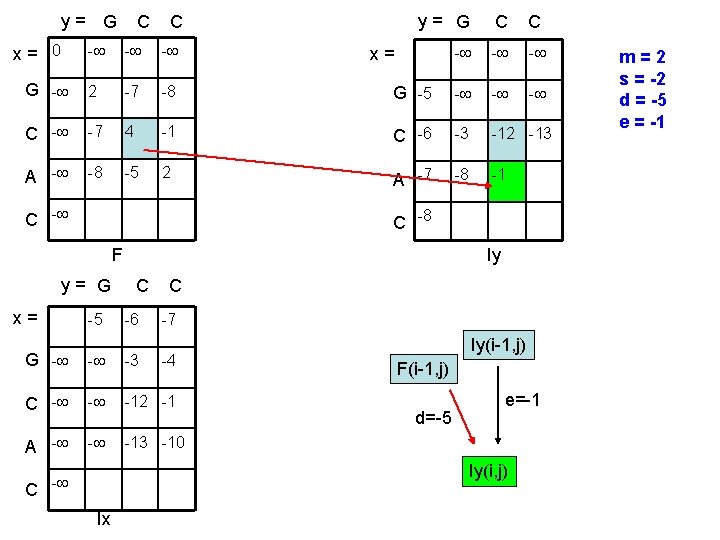
y= G x= 0 C C y= G C C - - G - 2 -7 -8 G -5 - - C - -7 4 -1 C -6 -3 -12 -13 A - -8 -5 2 A -7 -8 -1 C - x= C -8 F y= G x= -5 Iy C -6 C -7 G - - -3 C - - -12 -1 A - - -13 -10 -4 Iy(i-1, j) F(i-1, j) d=-5 e=-1 Iy(i, j) C - Ix m=2 s = -2 d = -5 e = -1

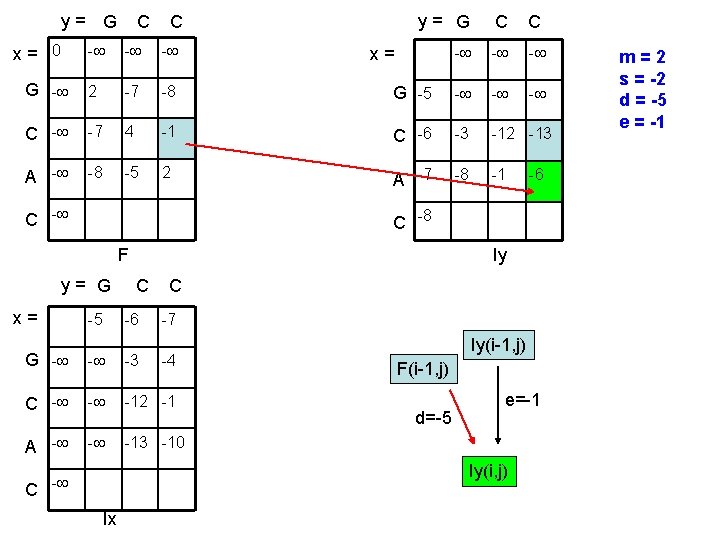
y= G x= 0 C C y= G C C - - G - 2 -7 -8 G -5 - - C - -7 4 -1 C -6 -3 -12 -13 A - -8 -5 2 A -7 -8 -1 C - x= C -8 F y= G x= -6 -5 Iy C -6 C -7 G - - -3 C - - -12 -1 A - - -13 -10 -4 Iy(i-1, j) F(i-1, j) d=-5 e=-1 Iy(i, j) C - Ix m=2 s = -2 d = -5 e = -1

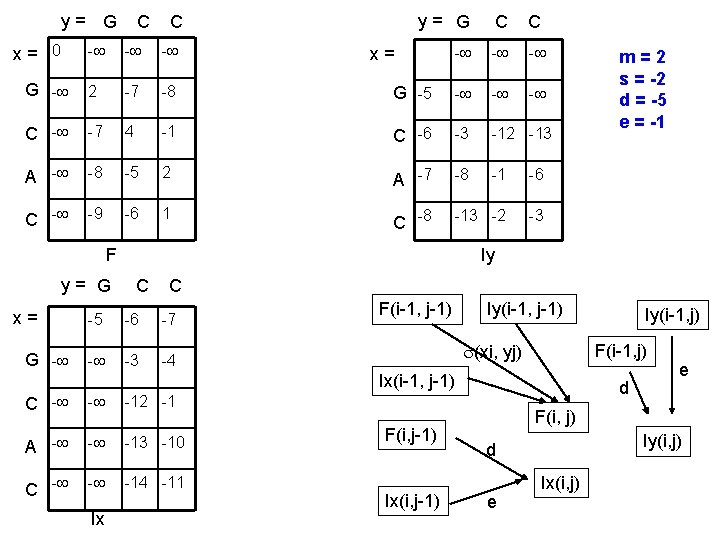
y= G x= 0 C C y= G C C - - G - 2 -7 -8 G -5 - - C - -7 4 -1 C -6 -3 -12 -13 A - -8 -5 2 A -7 -8 -1 -6 C - -9 -6 1 C -8 -13 -2 -3 x= F y= G x= G - Iy C C -5 -6 -7 - -3 -4 F(i-1, j-1) Iy(i-1, j-1) (xi, yj) C - - -12 -1 A - - -13 -10 C - - -14 -11 F(i, j-1) Ix(i, j-1) Iy(i-1, j) F(i-1, j) Ix(i-1, j-1) Ix m=2 s = -2 d = -5 e = -1 d e F(i, j) Iy(i, j) d e Ix(i, j)

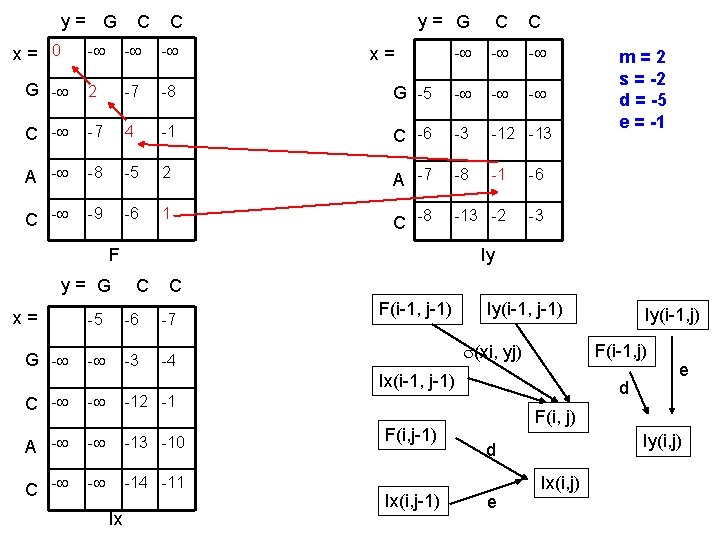
y= G x= 0 C C y= G C C - - G - 2 -7 -8 G -5 - - C - -7 4 -1 C -6 -3 -12 -13 A - -8 -5 2 A -7 -8 -1 -6 C - -9 -6 1 C -8 -13 -2 -3 x= F y= G x= G - Iy C C -5 -6 -7 - -3 -4 F(i-1, j-1) Iy(i-1, j-1) (xi, yj) C - - -12 -1 A - - -13 -10 C - - -14 -11 F(i, j-1) Ix(i, j-1) Iy(i-1, j) F(i-1, j) Ix(i-1, j-1) Ix m=2 s = -2 d = -5 e = -1 d e F(i, j) Iy(i, j) d e Ix(i, j)

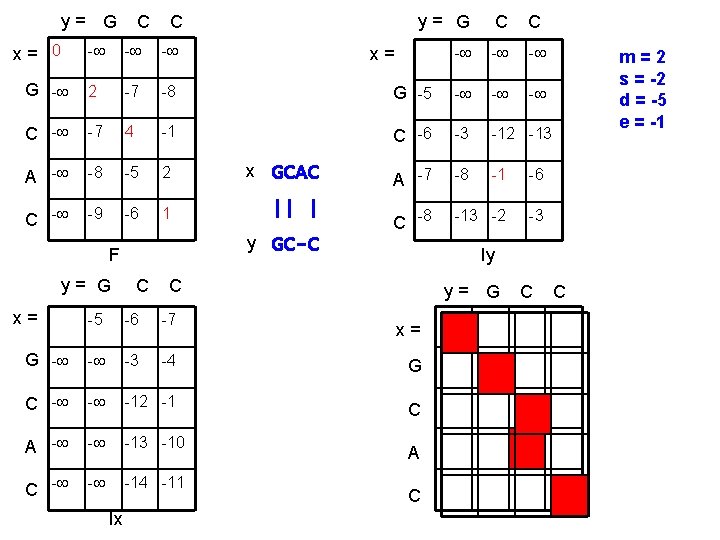
y= G x= 0 C C y= G C C - - G - 2 -7 -8 G -5 - - C - -7 4 -1 C -6 -3 -12 -13 A - -8 -5 2 x GCAC A -7 -8 -1 -6 C - -9 -6 1 || | C -8 -13 -2 -3 y GC-C F y= G x= x= C Iy C y= G -5 -6 -7 G - - -3 -4 G C - - -12 -1 C A - - -13 -10 C - - -14 -11 Ix m=2 s = -2 d = -5 e = -1 x= A C C C