CS 5263 Bioinformatics Lecture 4 Local Sequence Alignment

CS 5263 Bioinformatics Lecture 4: Local Sequence Alignment, More Efficient Sequence Alignment Algorithms

Roadmap • Review of last lecture • Local sequence alignment • More efficient sequence alignment algorithms

• Given a scoring scheme, – Match: m – Mismatch: -s – Gap: -d • We can easily compute an optimal alignment by dynamic programming

• Look at any column of an alignment between two sequences X = x 1 x 2…x. M, Y = y 1 y 1…y. N • Only three cases: – xi is aligned to yj – xi is aligned to a gap – yj is aligned to a gap F(i, j) = max F(i-1, j-1) + (xi, yj) F(i-1, j) - d F(i, j-1) - d

F(0, 0) F(M, N)

F(0, 0) F(M, N )

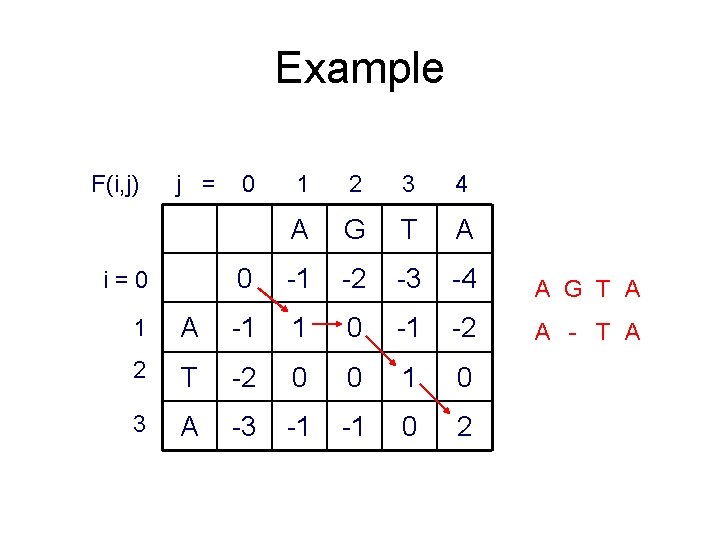
Example F(i, j) j = i=0 0 1 2 3 4 A G T A 0 -1 -2 -3 -4 A G T A A - T A 1 A -1 1 0 -1 -2 2 T -2 0 0 1 0 3 A -3 -1 -1 0 2

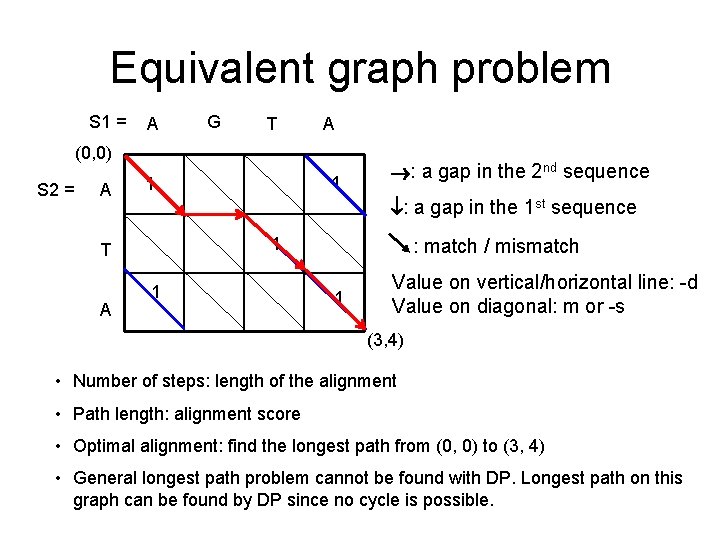
Equivalent graph problem S 1 = A G T A (0, 0) S 2 = A : a gap in the 1 st sequence 1 T A 1 1 : a gap in the 2 nd sequence 1 : match / mismatch 1 Value on vertical/horizontal line: -d Value on diagonal: m or -s (3, 4) • Number of steps: length of the alignment • Path length: alignment score • Optimal alignment: find the longest path from (0, 0) to (3, 4) • General longest path problem cannot be found with DP. Longest path on this graph can be found by DP since no cycle is possible.

Variants of Needleman-Wunsch alg • LCS: longest common subsequence – No penalty for gaps or mutations – Change: score function • Overlapping variants – No penalty for starting/ending gaps – Change: initial / termination step • Other variants – c. DNA-genome alignment

Local alignment

The local alignment problem Given two strings X = x 1……x. M, Y = y 1……y. N Find substrings x’, y’ whose similarity (optimal global alignment value) is maximum e. g. X = abcxdex Y = xxxcde x y X’ = cxde Y’ = c-de

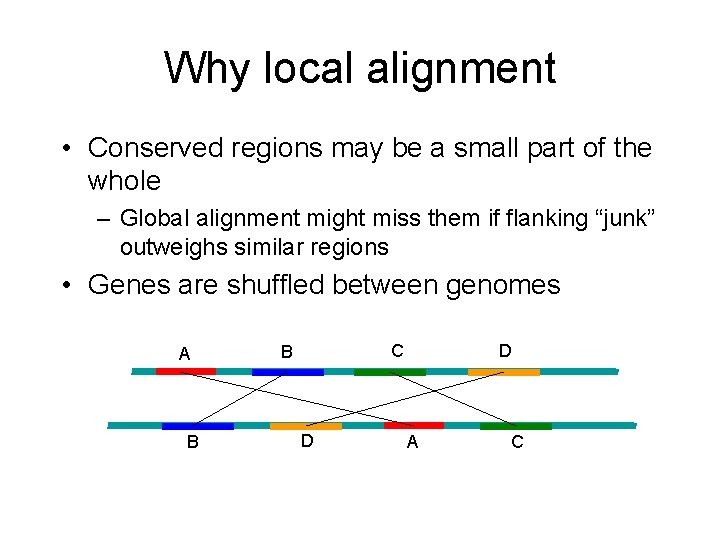
Why local alignment • Conserved regions may be a small part of the whole – Global alignment might miss them if flanking “junk” outweighs similar regions • Genes are shuffled between genomes A B C B D D A C

Naïve algorithm for all substrings X’ of X and Y’ of Y Align X’ & Y’ via dynamic programming Retain pair with max value end ; Output the retained pair • Time: O(n 2) choices for A, O(m 2) for B, O(nm) for DP, so O(n 3 m 3 ) total.

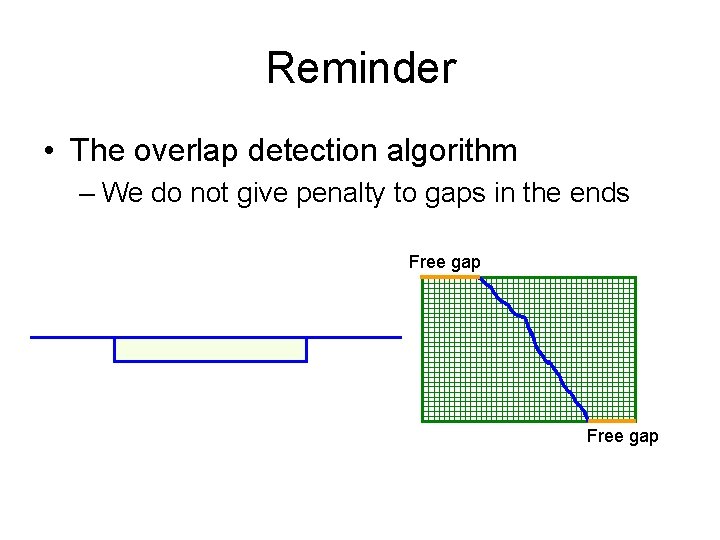
Reminder • The overlap detection algorithm – We do not give penalty to gaps in the ends Free gap

The local alignment idea • Do not penalize the unaligned regions (gaps or mismatches) • The alignment can start anywhere and ends anywhere • Strategy: whenever we get to some low similarity region (negative score), we restart a new alignment – By resetting alignment score to zero

The Smith-Waterman algorithm Initialization: F(0, j) = F(i, 0) = 0 0 F(i – 1, j) – d Iteration: F(i, j) = max F(i, j – 1) – d F(i – 1, j – 1) + (xi, yj)

The Smith-Waterman algorithm Termination: 1. If we want the best local alignment… FOPT = maxi, j F(i, j) 2. If we want all local alignments scoring > t For all i, j find F(i, j) > t, and trace back

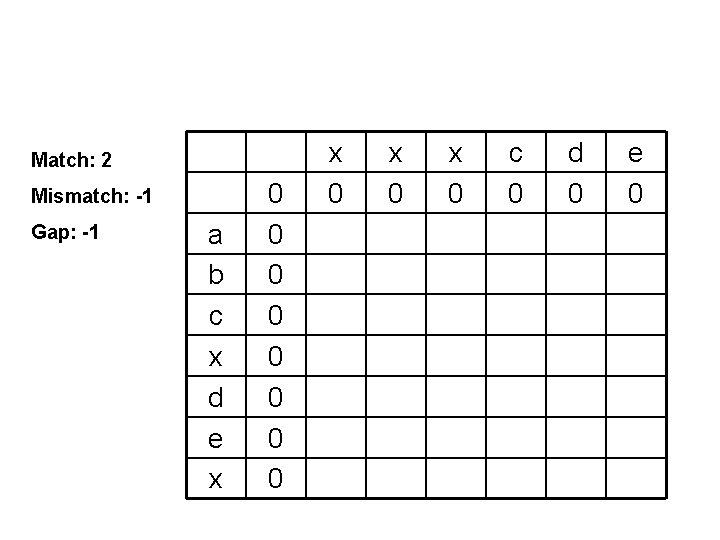
Match: 2 Mismatch: -1 Gap: -1 a b c x d e x 0 0 0 0 x 0 x 0 c 0 d 0 e 0

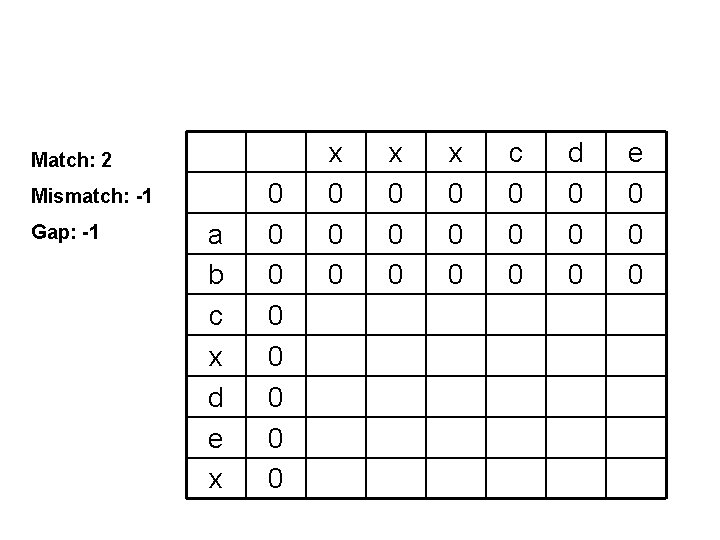
Match: 2 Mismatch: -1 Gap: -1 a b c x d e x 0 0 0 0 x 0 0 0 c 0 0 0 d 0 0 0 e 0 0 0

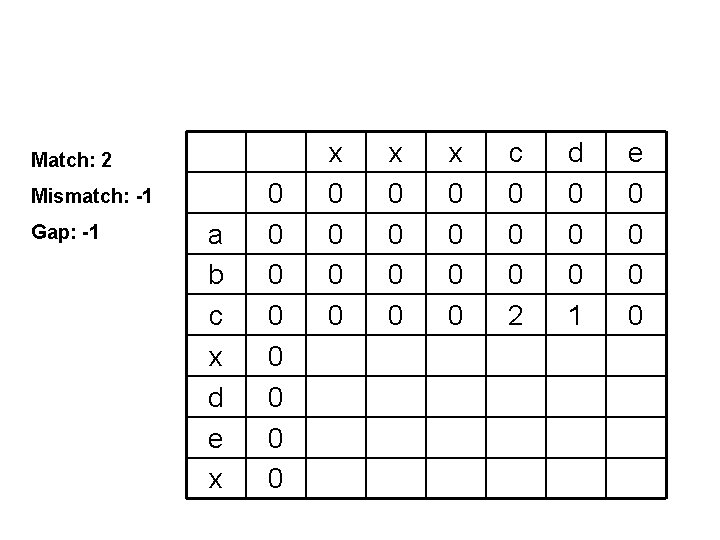
Match: 2 Mismatch: -1 Gap: -1 a b c x d e x 0 0 0 0 x 0 0 c 0 0 0 2 d 0 0 0 1 e 0 0

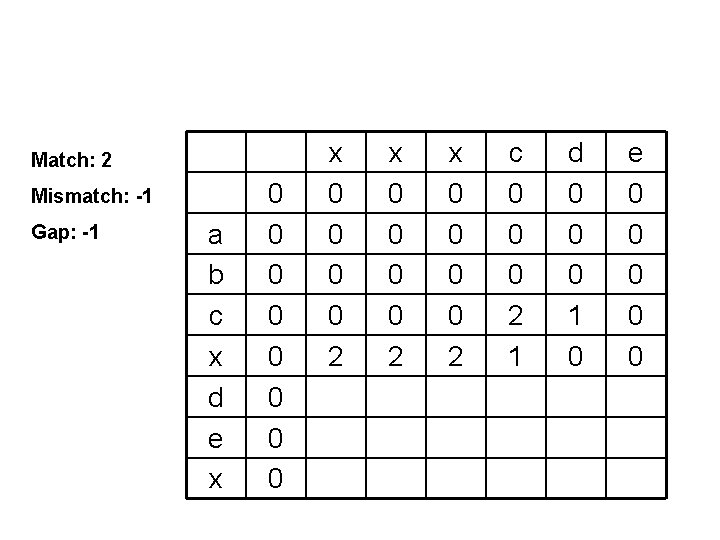
Match: 2 Mismatch: -1 Gap: -1 a b c x d e x 0 0 0 0 2 x 0 0 2 c 0 0 0 2 1 d 0 0 0 1 0 e 0 0 0

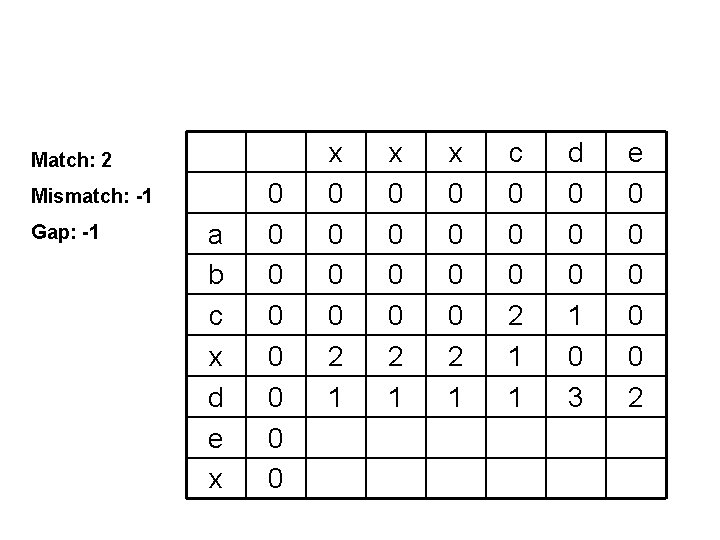
Match: 2 Mismatch: -1 Gap: -1 a b c x d e x 0 0 0 0 2 1 x 0 0 2 1 c 0 0 0 2 1 1 d 0 0 0 1 0 3 e 0 0 0 2

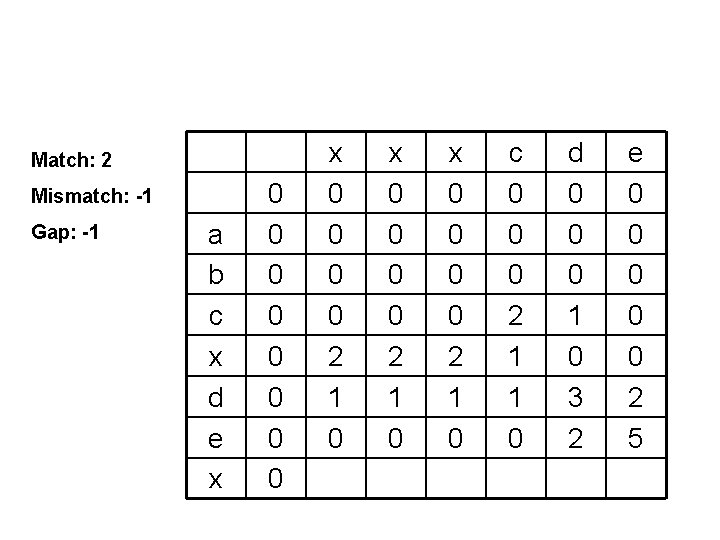
Match: 2 Mismatch: -1 Gap: -1 a b c x d e x 0 0 0 0 2 1 0 x 0 0 2 1 0 c 0 0 0 2 1 1 0 d 0 0 0 1 0 3 2 e 0 0 0 2 5

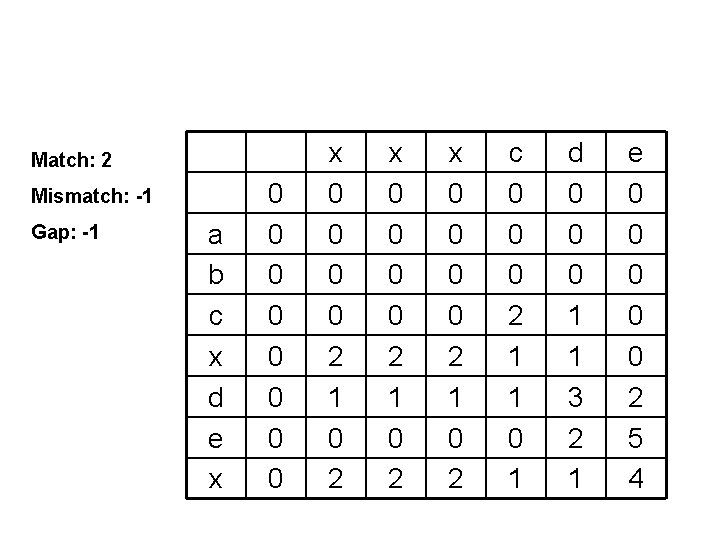
Match: 2 Mismatch: -1 Gap: -1 a b c x d e x 0 0 0 0 2 1 0 2 x 0 0 2 1 0 2 c 0 0 0 2 1 1 0 1 d 0 0 0 1 1 3 2 1 e 0 0 0 2 5 4

Trace back Match: 2 Mismatch: -1 Gap: -1 a b c x d e x 0 0 0 0 2 1 0 2 x 0 0 2 1 0 2 c 0 0 0 2 1 1 0 1 d 0 0 0 1 1 3 2 1 e 0 0 0 2 5 4

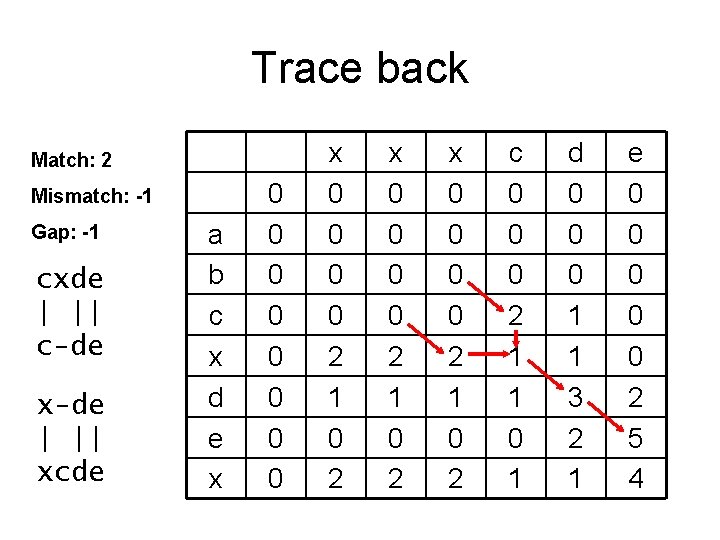
Trace back Match: 2 Mismatch: -1 Gap: -1 cxde | || c-de x-de | || xcde a b c x d e x 0 0 0 0 2 1 0 2 x 0 0 2 1 0 2 c 0 0 0 2 1 1 0 1 d 0 0 0 1 1 3 2 1 e 0 0 0 2 5 4

• No negative values in local alignment DP array • Optimal local alignment will never have a gap on either end • Local alignment: “Smith-Waterman” • Global alignment: “Needleman-Wunsch”

Analysis • Time: – O(MN) for finding the best alignment – Time to report all alignments depends on the number of sub-opt alignments • Memory: – O(MN) – O(M+N) possible

More efficient alignment algorithms

• Given two sequences of length M, N • Time: O(MN) – ok • Space: O(MN) – bad – 1 Mb seq x 1 Mb seq = 1000 G memory • Can we do better?

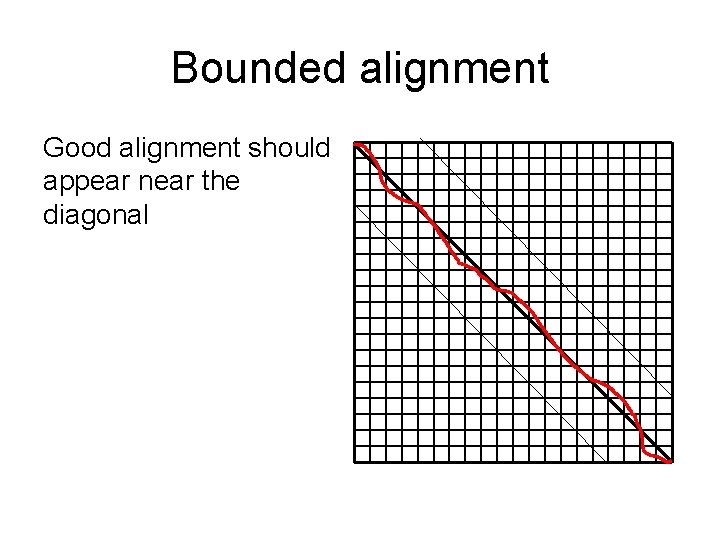
Bounded alignment Good alignment should appear near the diagonal

Bounded Dynamic Programming If we know that x and y are very similar Assumption: Then, xi | yj # gaps(x, y) < k implies |i–j|<k

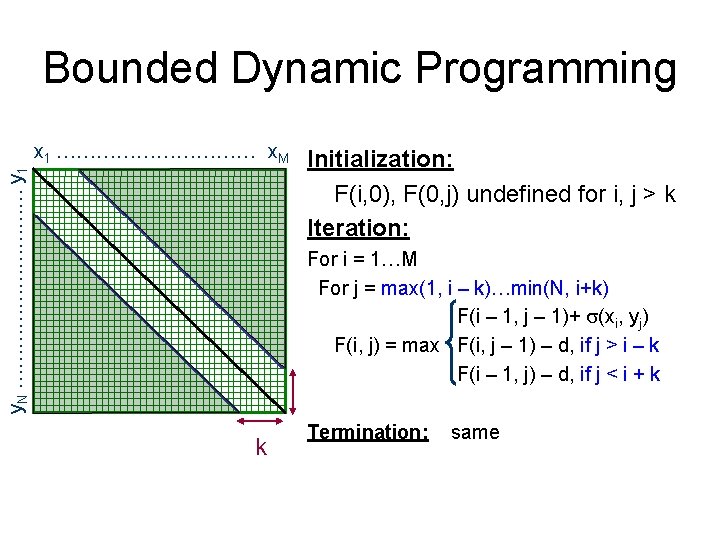
Bounded Dynamic Programming y. N …………… y 1 x 1 …………… x. M Initialization: F(i, 0), F(0, j) undefined for i, j > k Iteration: For i = 1…M For j = max(1, i – k)…min(N, i+k) F(i – 1, j – 1)+ (xi, yj) F(i, j) = max F(i, j – 1) – d, if j > i – k F(i – 1, j) – d, if j < i + k k Termination: same

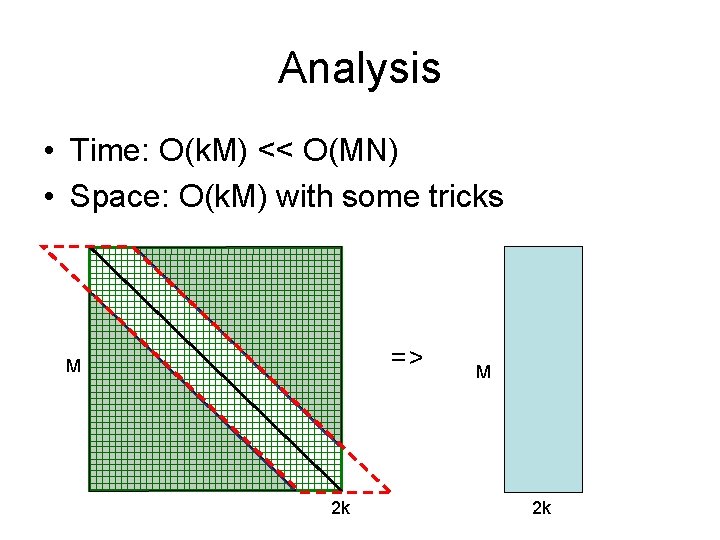
Analysis • Time: O(k. M) << O(MN) • Space: O(k. M) with some tricks => M 2 k

• Given two sequences of length M, N • Time: O(MN) – ok • Space: O(MN) – bad – 1 mb seq x 1 mb seq = 1000 G memory • Can we do better?

Linear space algorithm • If all we need is the alignment score but not the alignment, easy! We only need to keep two rows (You only need one row, with a little trick) But how do we get the alignment?

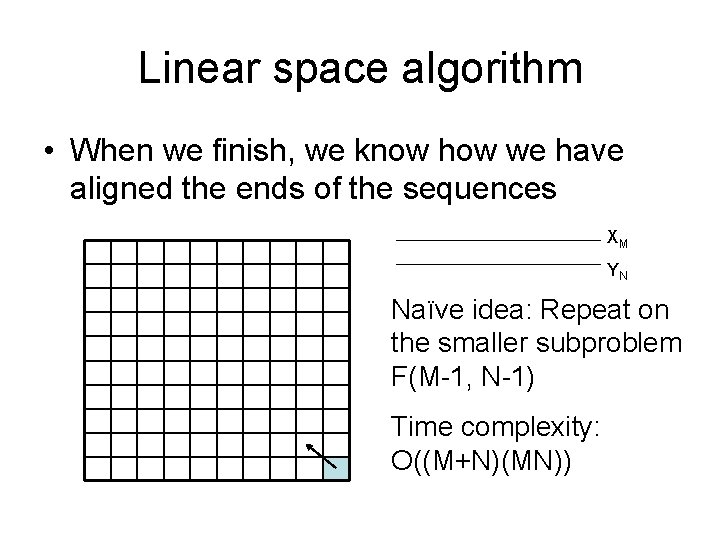
Linear space algorithm • When we finish, we know how we have aligned the ends of the sequences XM YN Naïve idea: Repeat on the smaller subproblem F(M-1, N-1) Time complexity: O((M+N)(MN))

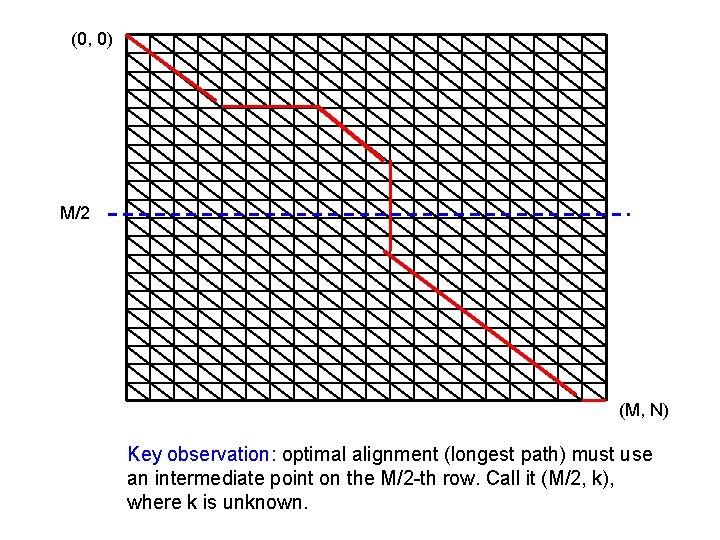
(0, 0) M/2 (M, N) Key observation: optimal alignment (longest path) must use an intermediate point on the M/2 -th row. Call it (M/2, k), where k is unknown.

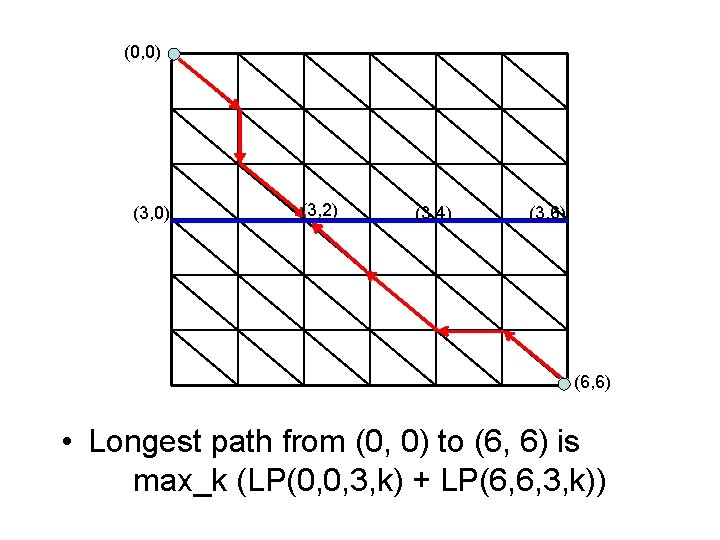
(0, 0) (3, 2) (3, 4) (3, 6) (6, 6) • Longest path from (0, 0) to (6, 6) is max_k (LP(0, 0, 3, k) + LP(6, 6, 3, k))

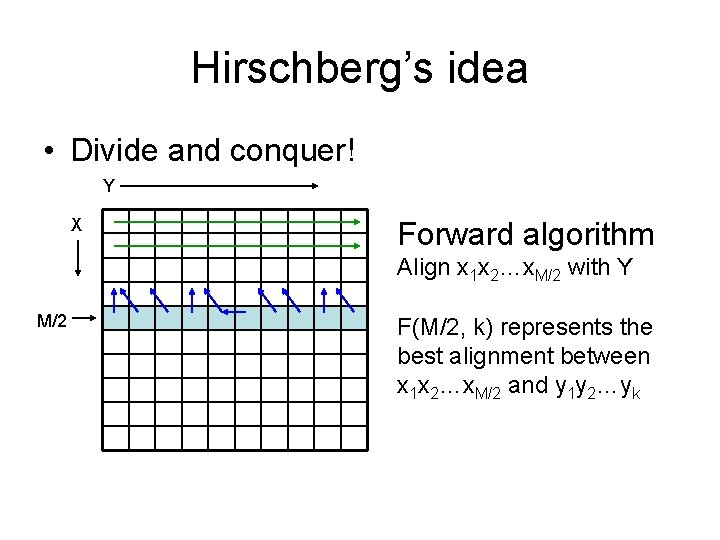
Hirschberg’s idea • Divide and conquer! Y X Forward algorithm Align x 1 x 2…x. M/2 with Y M/2 F(M/2, k) represents the best alignment between x 1 x 2…x. M/2 and y 1 y 2…yk

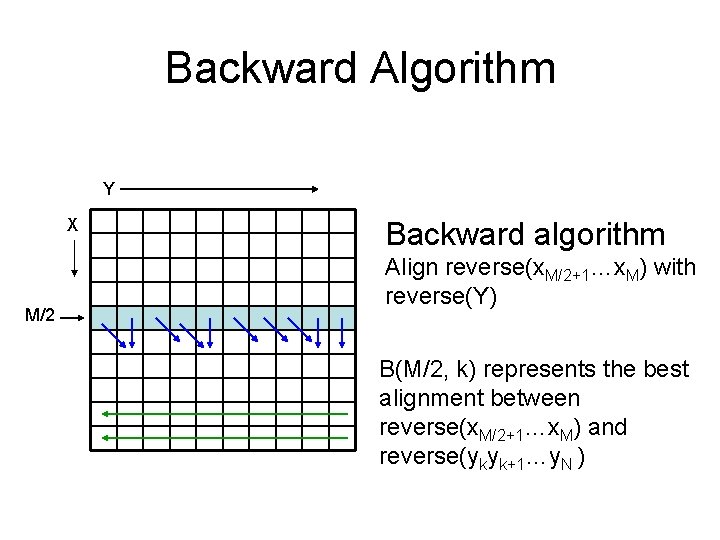
Backward Algorithm Y X M/2 Backward algorithm Align reverse(x. M/2+1…x. M) with reverse(Y) B(M/2, k) represents the best alignment between reverse(x. M/2+1…x. M) and reverse(ykyk+1…y. N )

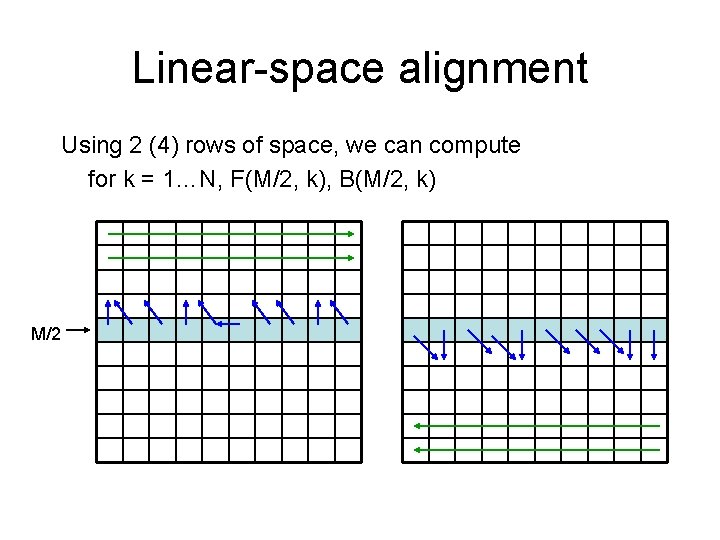
Linear-space alignment Using 2 (4) rows of space, we can compute for k = 1…N, F(M/2, k), B(M/2, k) M/2

Linear-space alignment Now, we can find k* maximizing F(M/2, k) + B(M/2, k) Also, we can trace the path exiting column M/2 from k* Conclusion: In O(NM) time, O(N) space, we found optimal alignment path at row M/2

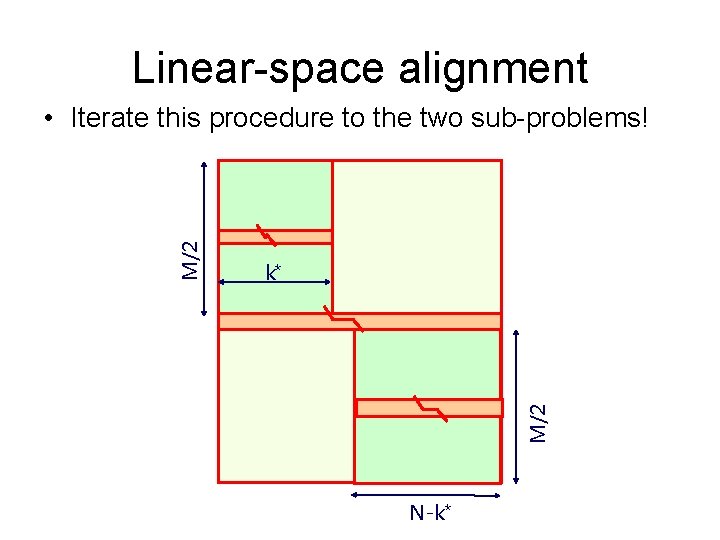
Linear-space alignment k* M/2 • Iterate this procedure to the two sub-problems! N-k*

Analysis • Memory: O(N) for computation, O(N+M) to store the optimal alignment • Time: – MN for first iteration – k M/2 + (N-k) M/2 = MN/2 for second –… k M/2 N-k

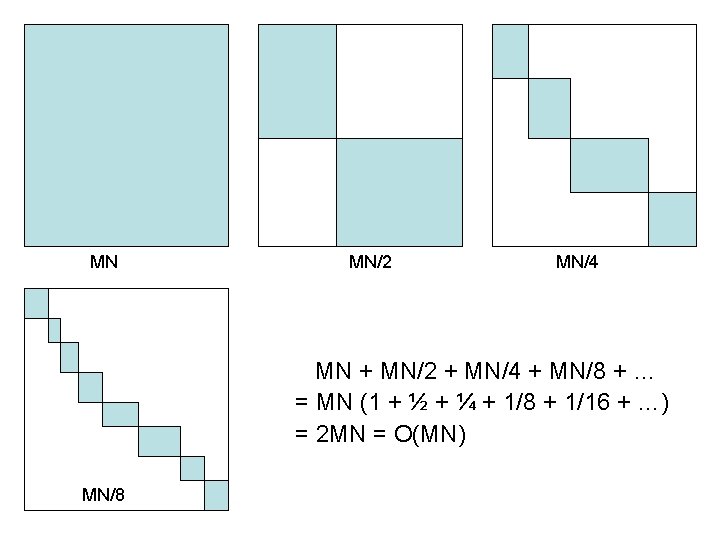
MN MN/2 MN/4 MN + MN/2 + MN/4 + MN/8 + … = MN (1 + ½ + ¼ + 1/8 + 1/16 + …) = 2 MN = O(MN) MN/8