CS 5205 Foundations in Programming Languages FP with

CS 5205: Foundations in Programming Languages FP with Haskell A pure lazy functional language that embodies many innovative ideas in language design. CS 5205 Haskell 1

Haskell • Advanced programming language – reusable, abstract, efficient, feature-rich. • Functions and Expressions • Values, Types and Lazy evaluation • Products, Records and Algebraic Types • Polymorphic Types & Type Classes • Higher-Order Functions • Infix operator and sections. Reference --- A Gentle Introduction to Haskell 98 http: //www. haskell. org/tutorial CS 5205 Haskell 2

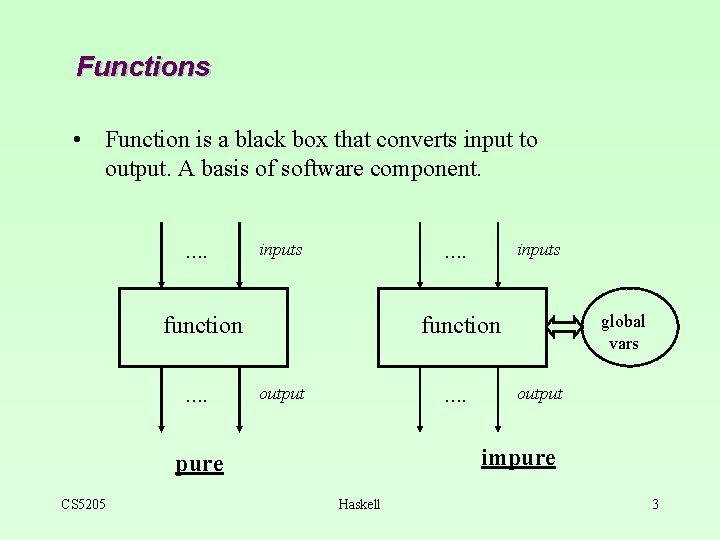
Functions • Function is a black box that converts input to output. A basis of software component. …. inputs function …. global vars function output …. output impure CS 5205 inputs …. Haskell 3

Example of Functions • Double a given input. square : : Int -> Int square x = x*x • Conversion from fahrenheit to celcius fahr_to_celcius : : Float -> Float fahr_to_celcius temp = (temp – 32)/1. 8 • A function with multiple results - quotient & remainder divide : : Int -> (Int, Int) divide x y = (div x y, mod x y) CS 5205 Haskell 4

Expression-Oriented • Instead of imperative commands/statements, the focus is on expression. • Instead of command/statement : if e 1 then stmt 1 else stmt 2 • We use conditional expressions : if e 1 then e 2 else e 3 CS 5205 Haskell 5

Expression-Oriented • An example function: fact n : : Integer -> Integer = if n=0 then 1 else n * fact (n-1) • Can use pattern-matching instead of conditional fact 0 fact n = 1 = n * fact (n-1) • Alternatively: fact n CS 5205 = case n of 0 -> 1 a -> a * fact (a-1) Haskell 6

Conditional Case Construct • Conditional; if e 1 then e 2 else e 3 • Can be translated to case e 1 of True -> e 2 False -> e 3 • Case also works over data structures (without any extra primitives) length xs = case xs of [] -> 0; y: ys -> 1+(length ys) Locally bound variables CS 5205 Haskell 7

Lexical Scoping • Local variables can be created by let construct to give nested scope for the name space. Example: let y = a+b f x = (x+y)/y in f c + f d • For scope bindings over guarded expressions, we require a where construct instead: f x y | x>z = … | y==z = … | y<z = …. where z=x*x CS 5205 Haskell 8

Layout Rule • Haskell uses two dimensional syntax that relies on declarations being “lined-up columnwise” let y = a+b f x = (x+y)/y in f c + f d is being parsed as: let { y = a+b ; f x = (x+y)/y } in f c + f d • Rule : Next character after keywords where/let/of/do determines the starting columns for declarations. Starting after this point continues a declaration, while starting before this point terminates a declaration. CS 5205 Haskell 9

Expression Evaluation • Expression can be computed (or evaluated) so that it is reduced to a value. This can be represented as: e . . v • We can abbreviate above as: e * v • A concrete example of this is: inc (inc 3) inc (4) 5 • Type preservation theorem says that: if e : : t Æ e v , it follows that v : : t CS 5205 Haskell 10

Values and Types • As a purely functional language, all computations are done via evaluating expressions (syntactic sugar) to yield values (normal forms as answers). • Each expression has a type which denotes the set of possible outcomes. • v : : t can be read as value v has type t. • Examples of typings, associating a value with its corresponding type are: 5 'a' [1, 2, 3] ('b', 4) “cs 5” CS 5205 : : : : : Integer Char [Integer] (Char, Integer) String (same as [Char]) Haskell 11

Built-In Types • They are not special: data Char = ‘a’ | ‘b’ | … data Int = -65532 | … | -1 | 0 | 1 | …. | 65532 data Integer = … | -2 | -1 | 0 | 1 | 2 | … • Tuples are also built-in. data (a, b) = M 2(a, b) data (a, b, c) = M 3(a, b, c) data (a, b. c. d) = M 4(a, b, c, d) • List type uses an infix operator: data [a] [1, 2, 3] CS 5205 = [] is short hand for Haskell | a : [a] 1 : (2 : (3 : [])) 12

User-Defined Algebraic Types • Can describe enumerations: data Bool data Color = False | True = Red | Green | Blue | Violet • Can also describe a tuple data Pair = P 2 Integer data Point a = Pt a a type variable • Pt is a data constructor with type a -> Point a Pt 2. 0 3. 1 Pt ‘a’ ‘b’ Pt True False CS 5205 : : Point Float : : Point Char : : Point Bool Haskell 13

Recursive Types • Some types may be recursive: data Tree a = Leaf a | Branch (Tree a) • Two data constructors: Leaf : : a -> Tree a Branch : : Tree a -> Tree a • An example function over recursive types: fringe : : Tree a -> [a] fringe (Leaf x) = [x] fringe (Branch left right) = (fringe left) ++ (fringe right) CS 5205 Haskell 14

Polymorphic Types • Support types that are universally quantified in some way over all types. • 8 c. [c] denotes a family of types, for every type c, the type of lists of c. • Covers [Integer], [Char], [Integer->Integer], etc. • Polymorphism help support reusable code, e. g length : : 8 a. [a] -> Integer length [] = 0 length (x: xs) = 1 + length xs CS 5205 Haskell 15

Polymorphic Types • This polymorphic function can be used on list of any type. . length [1, 2, 3] length [‘a’, ’b’, ‘c’] length [[1], [3]] ) ) ) 2 3 3 • More examples : head (x: xs) : : [a] -> a = x tail (x: xs) : : [a] -> [a] = xs • Note that head/tail are partial functions, while length is a total function? CS 5205 Haskell 16

Principal Types • Some types are more general than others: [Char] <: 8 a. [a] <: 8 a. a • An expression’s principal type is the least general type that contains all instances of the expression. • For example, the principal type of head function is [a]->a, while [b] -> a, b -> a, a are correct but too general but [Integer] -> Integer is too specific. • Principal type can help supports software reusability with accurate type information. CS 5205 Haskell 17

Type Synonyms • It is possible to provide new names for commonly used types type data String Person Name Address = = [Char] (Name, Address) String None | Addr String • Type synonyms do not define new types, but simply give new names for existing types. type Assoc. List a b = [(a, b)] • Their use can improve code readability. CS 5205 Haskell 18

Type Classes and Overloading • Parametric polymorphism works for all types. However, ad-hoc polymorphism works for a class of types and can systematically support overloading. • For example, what is the type for (+) operator? (+) : : a -> a (+) : : Int -> Int (+) : : Float -> Float • What about methods built from (+)? double x = x+x • Better solution is to use a type class for numerics! (+) : : Num a => a -> a double : : Num a => a -> a CS 5205 Haskell 19

Equality Class • Similar issue with equality. Though it looks like: (==) : : a -> Bool • Equality can be tested for data structures but not functions! • Solution is to define a type class that supports the equality method, as follows: class Eq a where (==), (/=) : : a -> Bool x /= y = not (x==y) default definition • Then: CS 5205 (==) : : Eq a => a -> Bool Haskell 20

Members of Eq Type Class • The class is open and can be extended, as follows: instance Eq Integer where x == y = x ‘integer. Eq’ y instance Eq Float where x == y = x ‘Float. Eq’ y • Recursive type can also be handled but elements may need to be given type qualifiers. instance (Eq a) => Eq (Tree a) where Leaf a == Leaf b = a==b (Branch l 1 r 1) == (Branch l 2 r 2) = (l 1==l 2) && (r 1==r 2) _ == _ = False CS 5205 Haskell 21

More Members of Eq Type Class • Similarly, we may use structural equality for List: instance (Eq a) => Eq [] == [] (x: xs) == (y: ys) _ == _ ([a]) where = True = (x==y) && (xs==ys) = False • One use of Eq class is: elem : : (Eq a) => a -> [a] -> Bool x ‘elem’ [] = False x ‘elem’ (y: ys) = (x==y) || (x ‘elem’ ys) • Exercise : define Set as an instance of the Eq class. CS 5205 Haskell 22

Numeric Class • There is a hierarchy of numeric classes. Most basic is: class Num a where (+), (-), (*) : : a -> a negate, abs, signum : : a -> a from. Integer : : Integer -> a x – y = x + (negate y) negate x = 0 – x instance … CS 5205 Num Int where Num Integer where Num Float where Num Double where Haskell 23

Functions and its Type • Method to increment its input inc x = x+1 • Or through lambda expression (anonymous functions) ( x -> x+1) • They can also be given suitable function typing: inc (x -> x+1) : : Num a => a -> a • Types can be user-supplied or inferred. CS 5205 Haskell 24

Functions and its Type • Some examples (x -> x+1) 3. 2 (x -> x+1) 3 • User can restrict the type, e. g. inc : : Int -> Int • In that case, some examples may be wrongly typed. inc 3. 2 inc 3 CS 5205 Haskell 25

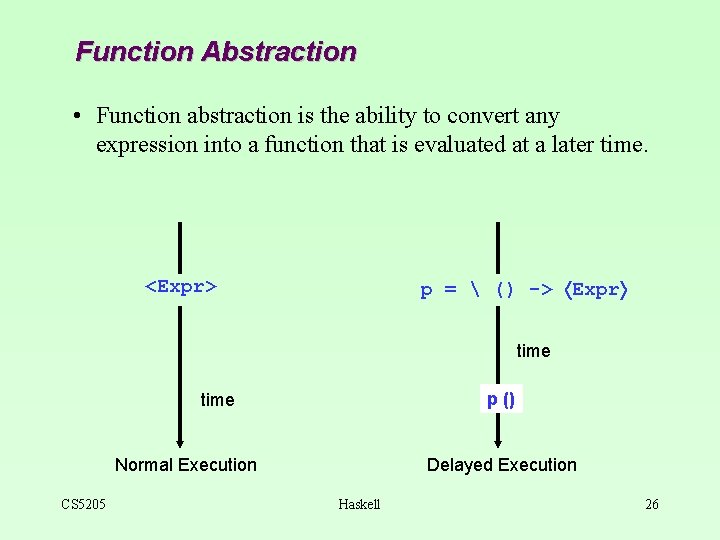
Function Abstraction • Function abstraction is the ability to convert any expression into a function that is evaluated at a later time. p = () -> Expr <Expr> time p () time Normal Execution CS 5205 Delayed Execution Haskell 26

Higher-Order Functions • Higher-order programming treats functions as first-class, allowing them to be passed as parameters, returned as results or stored into data structures. • This concept supports generic coding, and allows programming to be carried out at a more abstract level. • Genericity can be applied to a function by letting specific operation/value in the function body to become parameters. CS 5205 Haskell 27

Functions • Functions can be written in two main ways: add x y : : Integer -> Integer = x+y add 2(x, y) : : (Integer, Integer) -> Integer = x+y • The first version allows a function to be returned as result after applying a single argument. inc : : Integer -> Integer = add 1 • The second version needs all arguments. Same effect requires a lambda abstraction: inc CS 5205 = x -> add 2(x, 1) Haskell 28

Functions • Functions can also be passed as parameters. Example: map : : (a->b) -> [a] -> [b] map f [] = [] map f (x: xs) = (f x) : (map f xs) • Such higher-order function aids code reuse. map (add 1) [1, 2, 3] map add [1, 2, 3] ) [2, 3, 4] ) [add 1, add 2, add 3] • Alternative ways of defining functions: add CS 5205 = x -> y -> x+y = x y -> x+y Haskell 29

Genericity • Replace specific entities (0 and +) by parameters. sum. List ls = case ls of [] -> 0 x: xs -> x+(sum. List xs) foldr f u ls = case ls of [] -> u x: xs -> f x (foldr f u xs) CS 5205 Haskell 30

Polymorphic, Higher-Order Types sum. List : : [Int] -> Int sum. List : : Num a => [a] -> a foldr : : (a -> b) -> b -> [a] -> b CS 5205 Haskell 31

Instantiating Generic Functions sum. L 2 : : Num a => [a] -> a sum. L 2 ls = foldr (+) 0 ls sum. L 2 [1, 2, 3] ) sum. L 2 [1. 1, 3, 2. 3] ) CS 5205 Haskell 32

Instantiating Generic Functions prod. L : : Num a => [a] -> a prod. L ls = foldr (*) 1 ls prod. L [1, 2, 5] ) prod. L [1. 1, 3, 2. 3] ) CS 5205 Haskell 33

Instantiating Generic Functions • Can you express map in terms of foldr? map : : (a -> b) -> [a] -> [b] map f [] = [] map f (x: xs) = (f x) : (map f xs) map f xs CS 5205 = foldr … … … xs Haskell 34

Instantiating Generic Functions • Filtering a list of elements with a predicate. filter : : (a -> Bool) -> [a] filter f [] = [] filter f (x: xs) = if (f x) then x : (filter f xs) else x : filter f xs • Can we express filter in terms of foldr? filter f xs CS 5205 = foldr … … … xs Haskell 35

Pipe/Compose compose : : (b -> c) -> (a -> b) -> a -> c compose f g = x -> f (g x) g | f = compose f g • Similar to Unix pipe command: cmd 1 CS 5205 | cmd 2 Haskell 36

Iterator Construct for : : Int -> (Int -> a) -> a for i j f a = if i>j then a else f (i+1) j (f i a) • In Haskell, type class help give a more generic type: for : : Num b, Ord b => b -> (b -> a) -> a CS 5205 Haskell 37

Right Folding foldr f u [x 1, x 2, . . , xn] Þ f x 1 (foldr f u [x 2. . xn]) Þ f x 1 (f x 2 (fold f u [x 3. . xn])) Þ f x 1 (f x 2 (… (fold f u [xn]) …)) Þ f x 1 (f x 2 (… (f xn u) …))) associate to right CS 5205 Haskell 38

Left Folding – Tail Recursion • Accumulate result in a parameter: foldl f u ls = case ls of [] -> u x: xs -> foldl f (f u x) xs based on accumulation • What is the type of foldl? • Can we compute factorial using it? CS 5205 Haskell 39

Left Folding foldl f u [x 1, x 2, . . , xn] Þ foldl f (f u x 1) [x 2. . xn] Þ foldl f (f (f u x 1) x 2) [x 3. . xn])) Þ foldl f (f … (f (f u x 1) x 2)… xn) [] Þ f (… (f (f u x 1) x 2) …) xn left is here! CS 5205 Haskell 40

Instance of Left Folding • Summing a list by accumulation. sum. T acc ls = case ls of [] -> 0 x: xs -> sum. T (x+acc) xs sum. List ls = sum. T 0 ls sum. T acc ls = foldl (+) acc ls CS 5205 Haskell 41

Infix Operator • Infix operators are distinguished entirely by symbols: (++) [] ++ ys (x: xs) ++ ys : : [a]-> [a] = ys = x : (xs ++ ys) • Another example is function composition. (. ) f. g : : (b->c) -> (a->b) -> (a->c) = x -> f (g x) • Infix operator can be coerced to prefix by bracketing, e. g. map (+) [1, 2, 3] • Alphanumeric named function can be made infix too, e. g. a ‘add’ b x ‘elem’ xs CS 5205 Haskell 42

Sections • Infix operators can also be partially applied: (x+) (+y) (+) ´ ´ ´ y -> x+y x y -> x+y = = (+ 1) (+) • Other examples: . inc add • These are syntactic sugar for programming conveniences. CS 5205 Haskell 43