CS 4803 7643 Deep Learning Topics Finish Analytical

CS 4803 / 7643: Deep Learning Topics: – (Finish) Analytical Gradients – Automatic Differentiation – Computational Graphs – Forward mode vs Reverse mode AD Dhruv Batra Georgia Tech

Administrativia • HW 1 Reminder – Due: 09/26, 11: 55 pm • Fuller schedule + future reading posted – https: //www. cc. gatech. edu/classes/AY 2020/cs 7643_fall/ – Caveat: subject to change; please don’t make irreversible decisions based on this. (C) Dhruv Batra 2

Recap from last time (C) Dhruv Batra 3

Strategy: Follow the slope Slide Credit: Fei-Fei Li, Justin Johnson, Serena Yeung, CS 231 n

Gradient Descent Slide Credit: Fei-Fei Li, Justin Johnson, Serena Yeung, CS 231 n

Stochastic Gradient Descent (SGD) Full sum expensive when N is large! Approximate sum using a minibatch of examples 32 / 64 / 128 common Slide Credit: Fei-Fei Li, Justin Johnson, Serena Yeung, CS 231 n

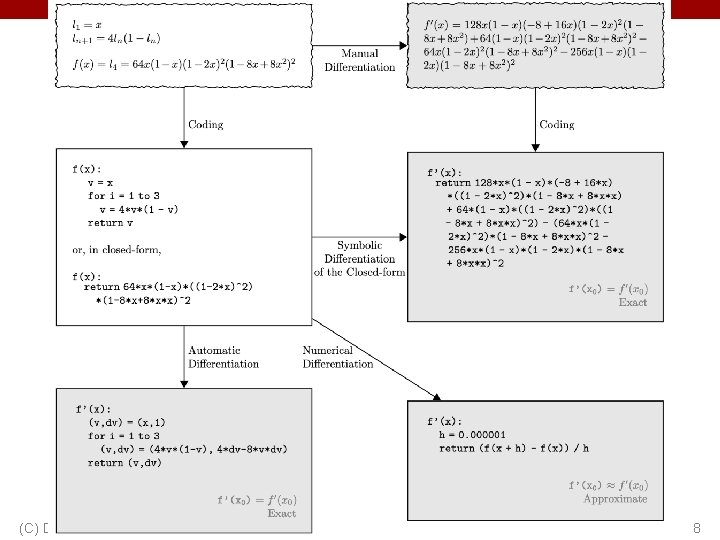
How do we compute gradients? • Analytic or “Manual” Differentiation • Symbolic Differentiation • Numerical Differentiation • Automatic Differentiation – Forward mode AD – Reverse mode AD • aka “backprop” (C) Dhruv Batra 7

(C) Dhruv Batra Figure Credit: Baydin et al. https: //arxiv. org/abs/1502. 05767 8

How do we compute gradients? • Analytic or “Manual” Differentiation • Symbolic Differentiation • Numerical Differentiation • Automatic Differentiation – Forward mode AD – Reverse mode AD • aka “backprop” (C) Dhruv Batra 9

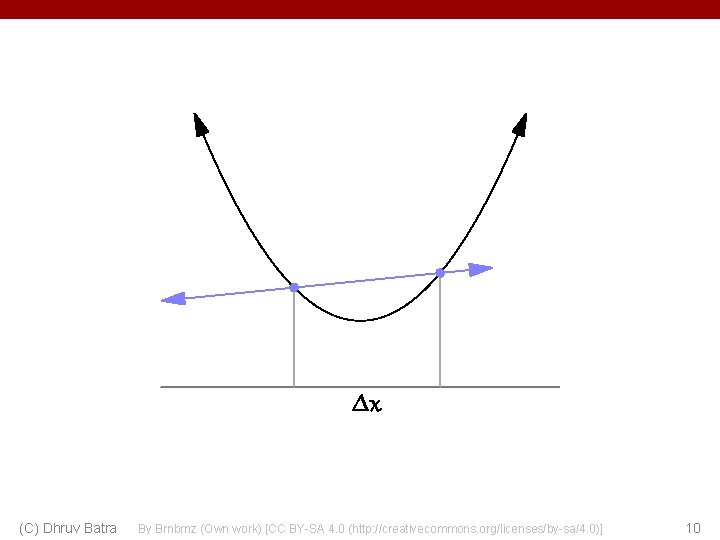
(C) Dhruv Batra By Brnbrnz (Own work) [CC BY-SA 4. 0 (http: //creativecommons. org/licenses/by-sa/4. 0)] 10

current W: W + h (first dim): [0. 34, -1. 11, 0. 78, 0. 12, 0. 55, 2. 81, -3. 1, -1. 5, 0. 33, …] loss 1. 25347 [0. 34 + 0. 0001, -1. 11, 0. 78, 0. 12, 0. 55, 2. 81, -3. 1, -1. 5, 0. 33, …] loss 1. 25322 gradient d. W: [-2. 5, ? , ? , - 1. 25347)/0. 0001 (1. 25322 = -2. 5 ? , ? , ? , …] Slide Credit: Fei-Fei Li, Justin Johnson, Serena Yeung, CS 231 n

current W: W + h (second dim): [0. 34, -1. 11, 0. 78, 0. 12, 0. 55, 2. 81, -3. 1, -1. 5, 0. 33, …] loss 1. 25347 [0. 34, -1. 11 + 0. 0001, 0. 78, 0. 12, 0. 55, 2. 81, -3. 1, -1. 5, 0. 33, …] loss 1. 25353 gradient d. W: [-2. 5, 0. 6, ? , (1. 25353 ? , - 1. 25347)/0. 0001 = 0. 6 ? , ? , …] Slide Credit: Fei-Fei Li, Justin Johnson, Serena Yeung, CS 231 n

Numerical vs Analytic Gradients Numerical gradient: slow : (, approximate : (, easy to write : ) Analytic gradient: fast : ), exact : ), error-prone : ( In practice: Derive analytic gradient, check your implementation with numerical gradient. This is called a gradient check. Slide Credit: Fei-Fei Li, Justin Johnson, Serena Yeung, CS 231 n

How do we compute gradients? • Analytic or “Manual” Differentiation • Symbolic Differentiation • Numerical Differentiation • Automatic Differentiation – Forward mode AD – Reverse mode AD • aka “backprop” (C) Dhruv Batra 14

Matrix/Vector Derivatives Notation (C) Dhruv Batra 15

Vector/Matrix Derivatives Notation (C) Dhruv Batra 16

Vector Derivative Example (C) Dhruv Batra 17

Vector Derivative Example (C) Dhruv Batra 18

Extension to Tensors (C) Dhruv Batra 19

Plan for Today • (Finish) Analytical Gradients • Automatic Differentiation – Computational Graphs – Forward mode vs Reverse mode AD – Patterns in backprop (C) Dhruv Batra 20

Chain Rule: Composite Functions (C) Dhruv Batra 21

Chain Rule: Scalar Case (C) Dhruv Batra 22

Chain Rule: Vector Case (C) Dhruv Batra 23

Chain Rule: Jacobian view (C) Dhruv Batra 24

Chain Rule: Graphical view (C) Dhruv Batra 25

(C) Dhruv Batra 26

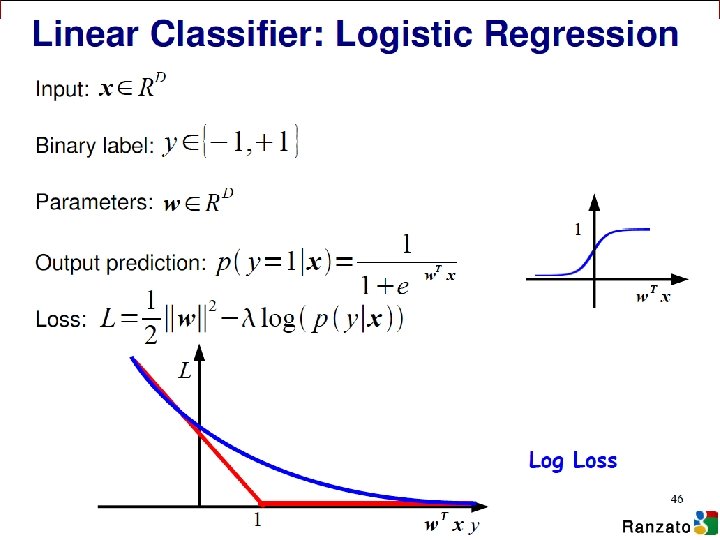
Logistic Regression Derivatives (C) Dhruv Batra 27

Logistic Regression Derivatives (C) Dhruv Batra 28

Chain Rule: Cascaded (C) Dhruv Batra 29

Chain Rule: How should we multiply? (C) Dhruv Batra 30

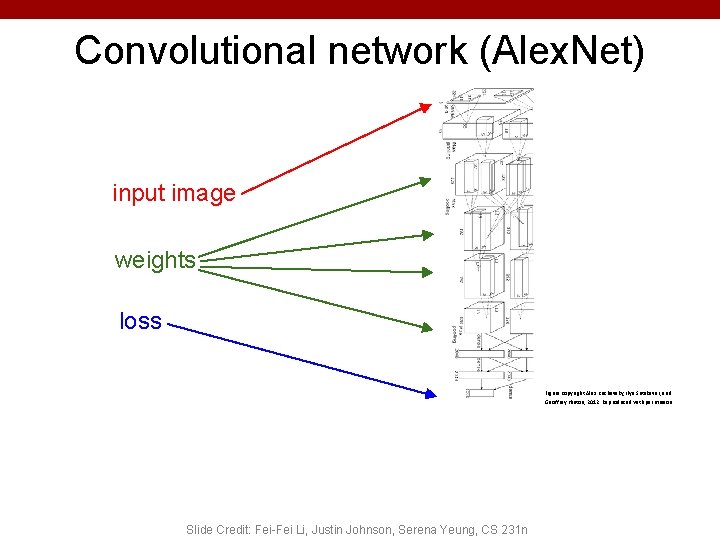
Convolutional network (Alex. Net) input image weights loss Figure copyright Alex Krizhevsky, Ilya Sutskever, and Geoffrey Hinton, 2012. Reproduced with permission. Slide Credit: Fei-Fei Li, Justin Johnson, Serena Yeung, CS 231 n

Neural Turing Machine input image loss Figure reproduced with permission from a Twitter post by Andrej Karpathy. Slide Credit: Fei-Fei Li, Justin Johnson, Serena Yeung, CS 231 n

How do we compute gradients? • Analytic or “Manual” Differentiation • Symbolic Differentiation • Numerical Differentiation • Automatic Differentiation – Forward mode AD – Reverse mode AD • aka “backprop” (C) Dhruv Batra 33

Plan for Today • (Finish) Analytical Gradients • Automatic Differentiation – Computational Graphs – Forward mode vs Reverse mode AD (C) Dhruv Batra 34

Deep Learning = Differentiable Programming • Computation = Graph – Input = Data + Parameters – Output = Loss – Scheduling = Topological ordering • Auto-Diff – A family of algorithms for implementing chain-rule on computation graphs (C) Dhruv Batra 35

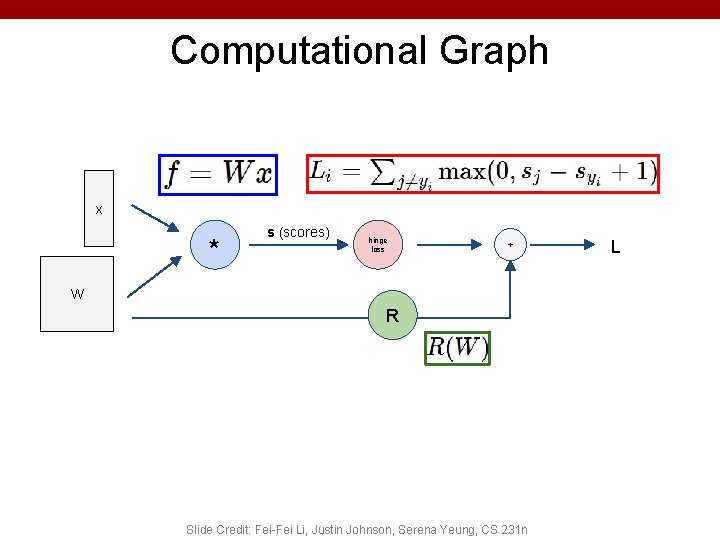
Computational Graph x * s (scores) hinge loss + W R Slide Credit: Fei-Fei Li, Justin Johnson, Serena Yeung, CS 231 n L

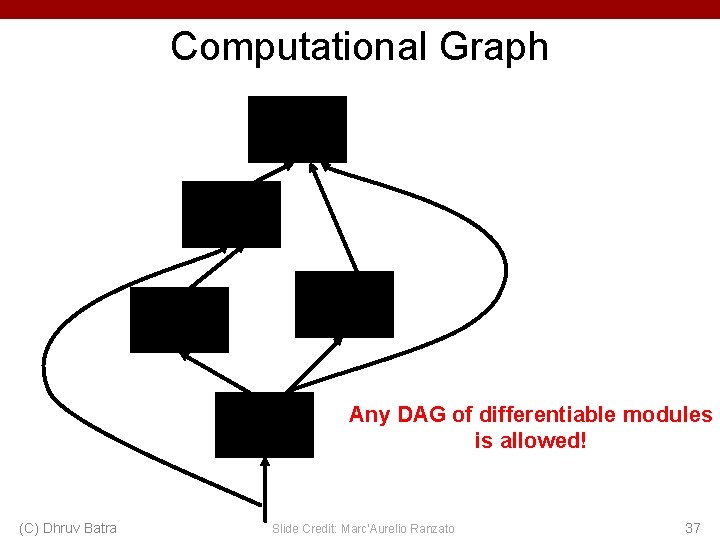
Computational Graph Any DAG of differentiable modules is allowed! (C) Dhruv Batra Slide Credit: Marc'Aurelio Ranzato 37

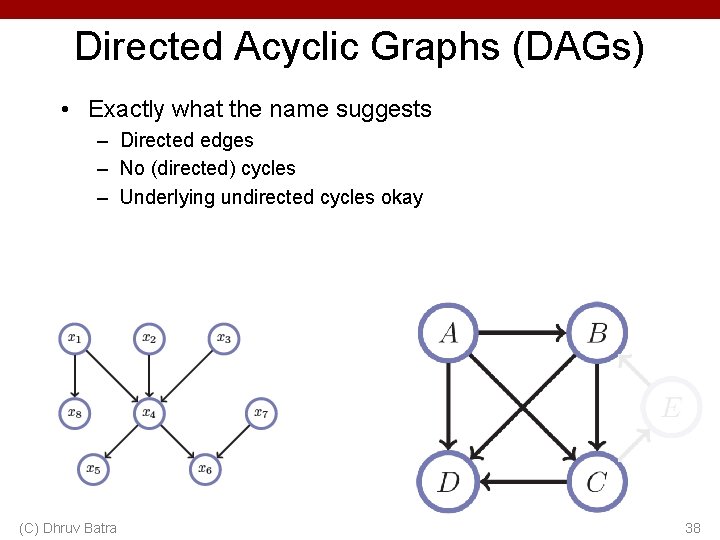
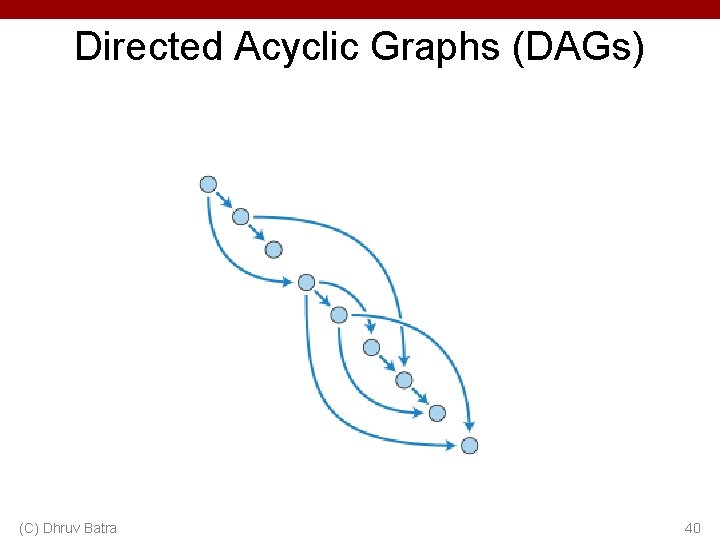
Directed Acyclic Graphs (DAGs) • Exactly what the name suggests – Directed edges – No (directed) cycles – Underlying undirected cycles okay (C) Dhruv Batra 38

Directed Acyclic Graphs (DAGs) • Concept – Topological Ordering (C) Dhruv Batra 39

Directed Acyclic Graphs (DAGs) (C) Dhruv Batra 40

Computational Graphs • Notation (C) Dhruv Batra 41

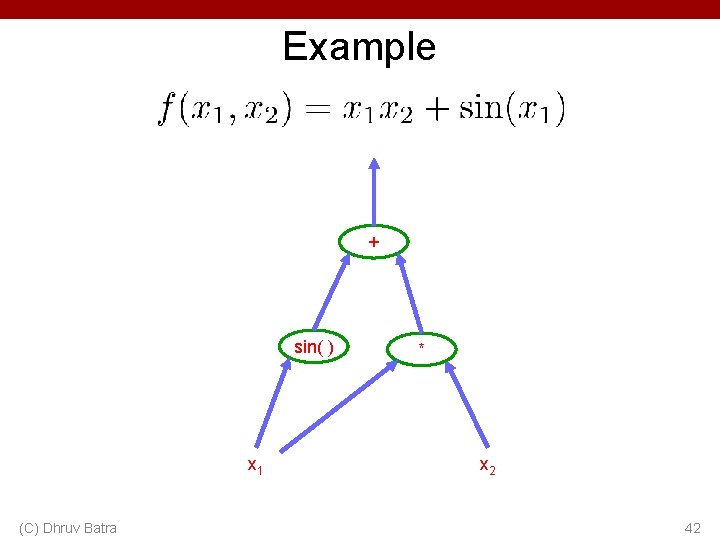
Example + sin( ) x 1 (C) Dhruv Batra * x 2 42

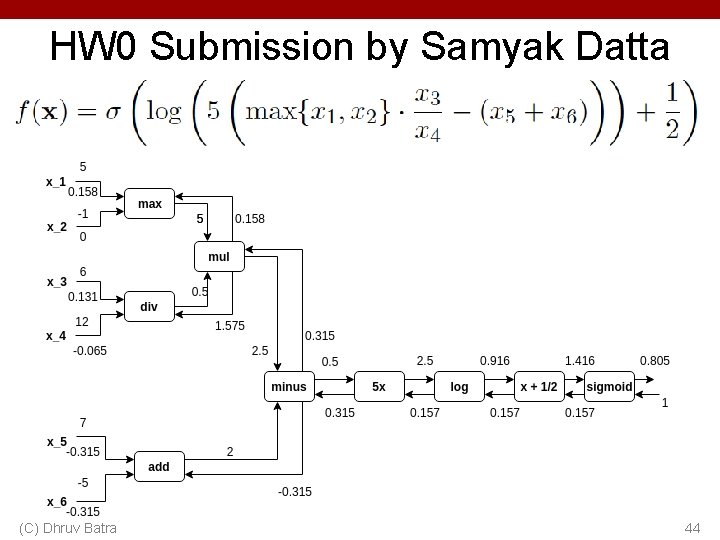
HW 0 (C) Dhruv Batra 43

HW 0 Submission by Samyak Datta (C) Dhruv Batra 44

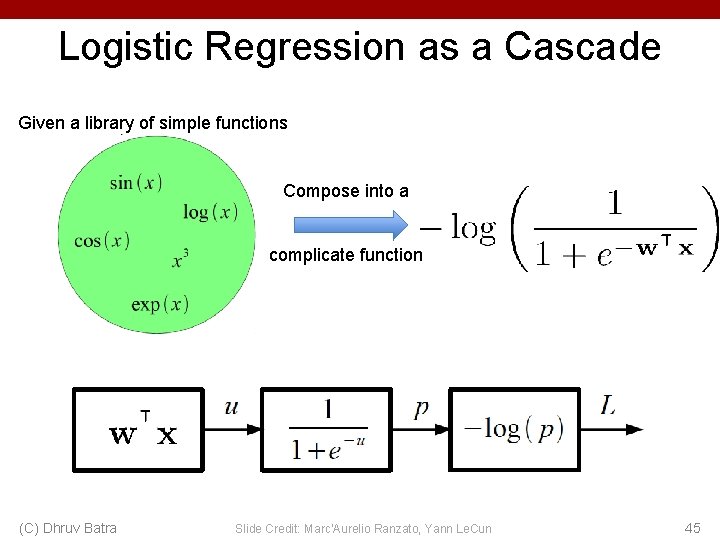
Logistic Regression as a Cascade Given a library of simple functions Compose into a complicate function (C) Dhruv Batra Slide Credit: Marc'Aurelio Ranzato, Yann Le. Cun 45

Deep Learning = Differentiable Programming • Computation = Graph – Input = Data + Parameters – Output = Loss – Scheduling = Topological ordering • Auto-Diff – A family of algorithms for implementing chain-rule on computation graphs (C) Dhruv Batra 46

Forward mode vs Reverse Mode • Key Computations (C) Dhruv Batra 47

Forward mode AD g 48

Reverse mode AD g 49

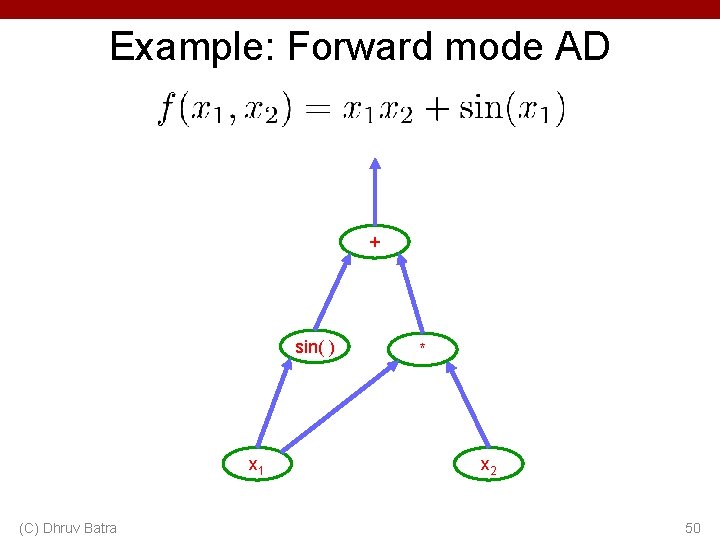
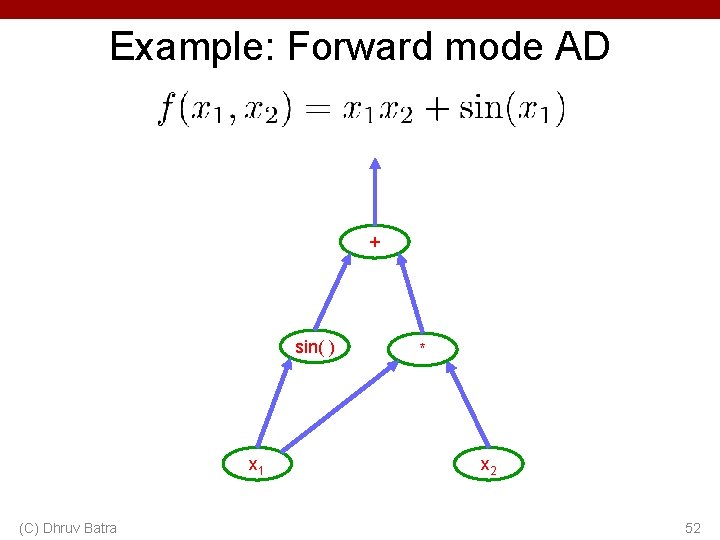
Example: Forward mode AD + sin( ) x 1 (C) Dhruv Batra * x 2 50

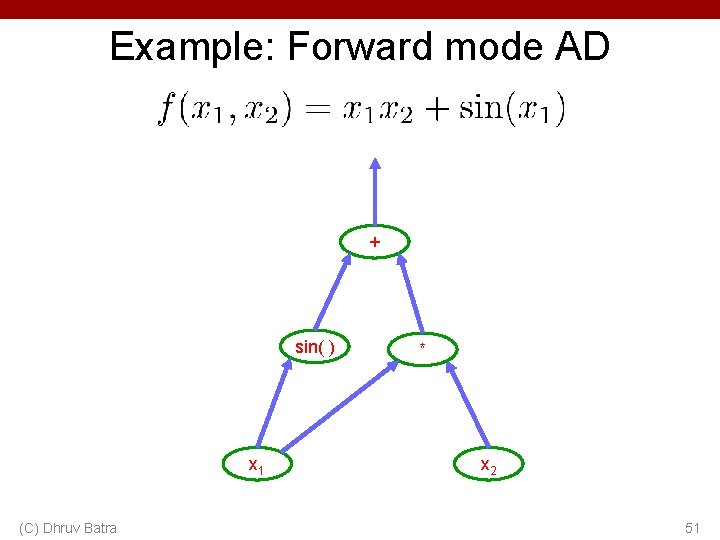
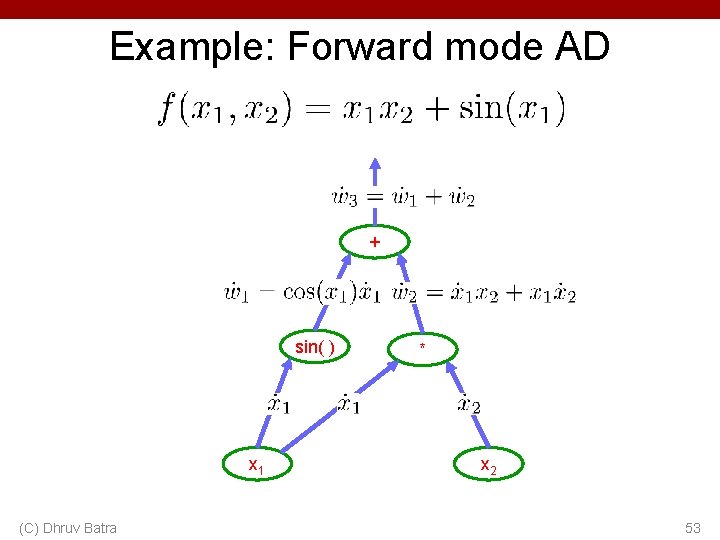
Example: Forward mode AD + sin( ) x 1 (C) Dhruv Batra * x 2 51

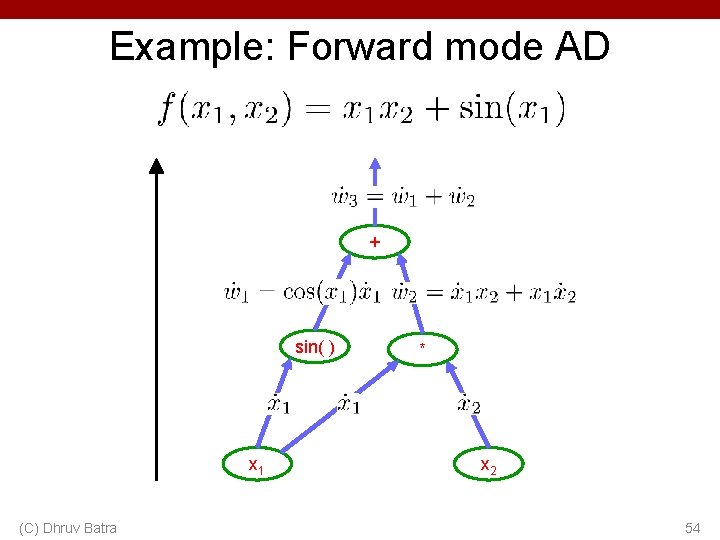
Example: Forward mode AD + sin( ) x 1 (C) Dhruv Batra * x 2 52

Example: Forward mode AD + sin( ) x 1 (C) Dhruv Batra * x 2 53

Example: Forward mode AD + sin( ) x 1 (C) Dhruv Batra * x 2 54

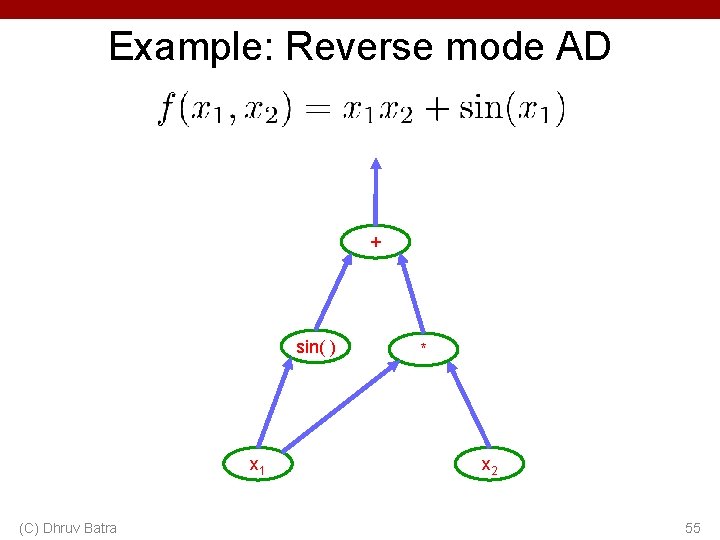
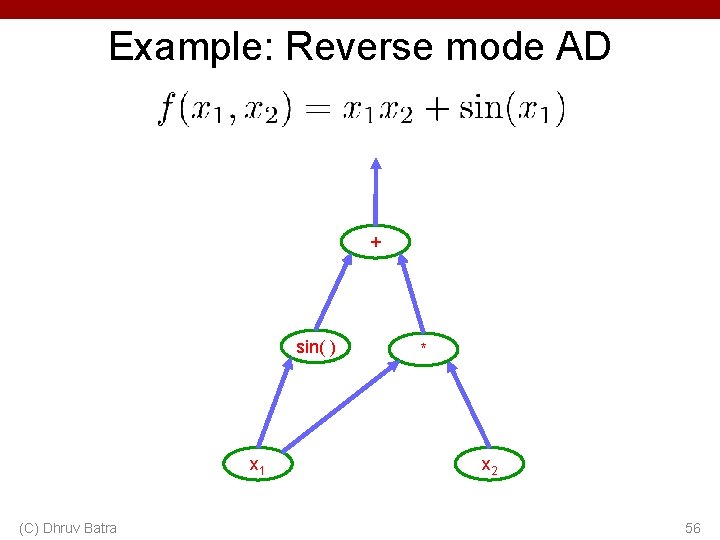
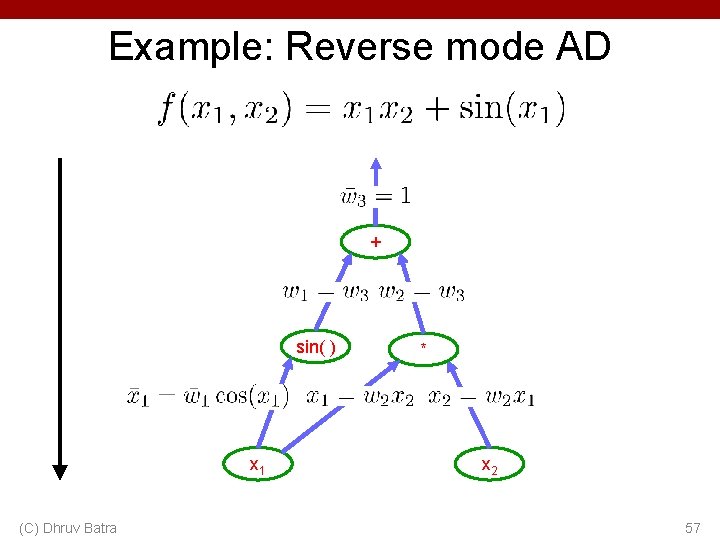
Example: Reverse mode AD + sin( ) x 1 (C) Dhruv Batra * x 2 55

Example: Reverse mode AD + sin( ) x 1 (C) Dhruv Batra * x 2 56

Example: Reverse mode AD + sin( ) x 1 (C) Dhruv Batra * x 2 57

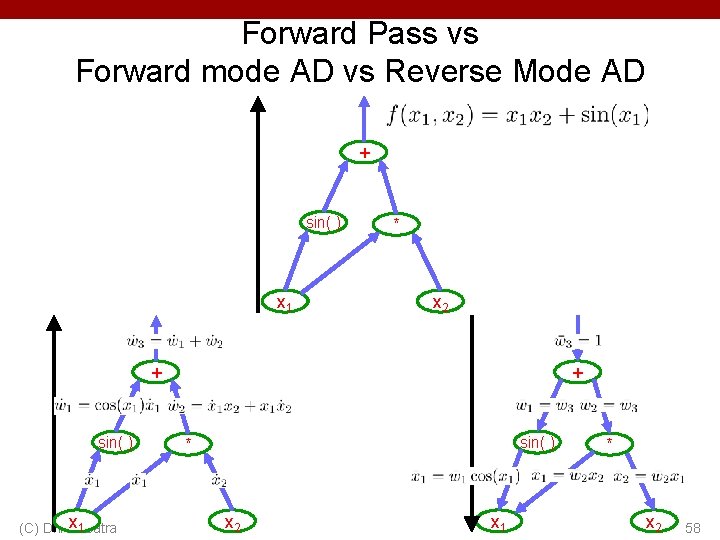
Forward Pass vs Forward mode AD vs Reverse Mode AD + sin( ) x 1 * x 2 + sin( ) x 1 Batra (C) Dhruv + sin( ) * x 2 x 1 * x 2 58

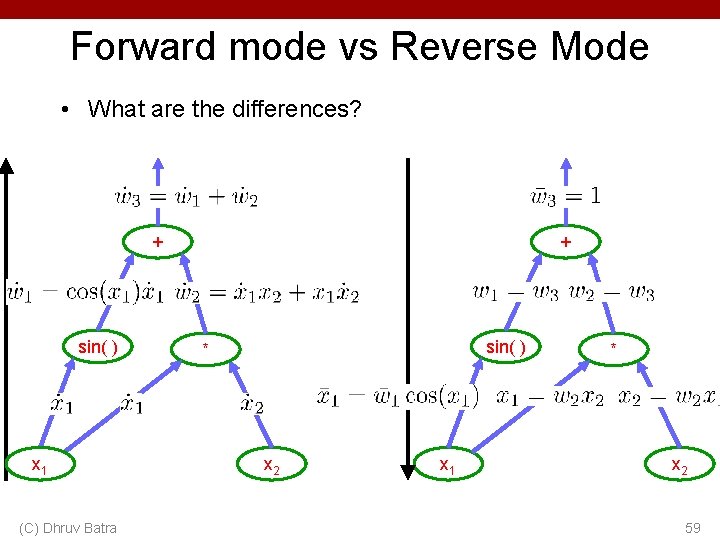
Forward mode vs Reverse Mode • What are the differences? + sin( ) x 1 (C) Dhruv Batra + sin( ) * x 2 x 1 * x 2 59

Forward mode vs Reverse Mode • What are the differences? • Which one is faster to compute? – Forward or backward? (C) Dhruv Batra 60

Forward mode vs Reverse Mode • What are the differences? • Which one is faster to compute? – Forward or backward? • Which one is more memory efficient (less storage)? – Forward or backward? (C) Dhruv Batra 61