CS 455 Computer Graphics Window to Viewport Transformations

CS 455 – Computer Graphics Window to Viewport Transformations

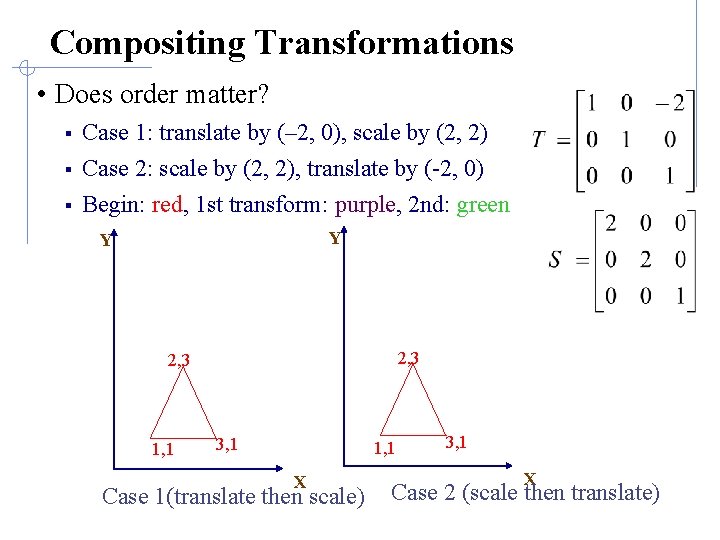
Compositing Transformations • Does order matter? § Case 1: translate by (– 2, 0), scale by (2, 2) § Case 2: scale by (2, 2), translate by (-2, 0) Begin: red, 1 st transform: purple, 2 nd: green § Y Y 2, 3 1, 1 3, 1 1, 1 X Case 1(translate then scale) 3, 1 X Case 2 (scale then translate)

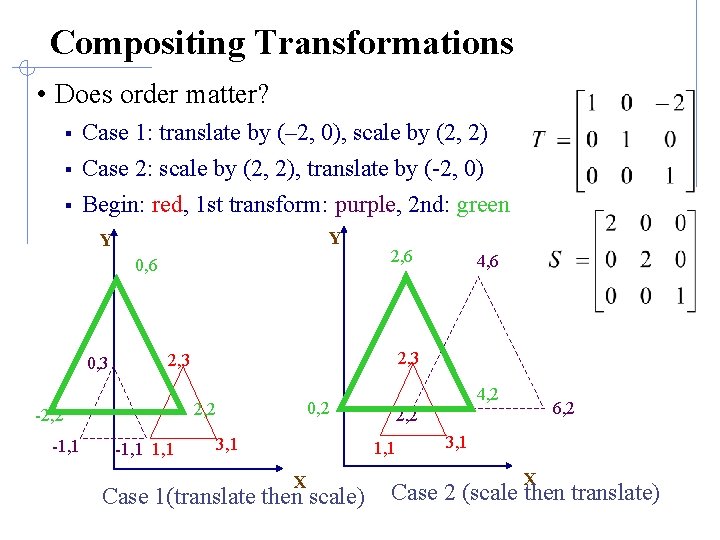
Compositing Transformations • Does order matter? § Case 1: translate by (– 2, 0), scale by (2, 2) § Case 2: scale by (2, 2), translate by (-2, 0) Begin: red, 1 st transform: purple, 2 nd: green § Y Y 0, 6 0, 3 0, 2 2, 2 -1, 1 4, 6 2, 3 -2, 2 -1, 1 2, 6 3, 1 4, 2 1, 1 X Case 1(translate then scale) 6, 2 2, 2 3, 1 X Case 2 (scale then translate)

Composition Example Scale(2. 0, 2. 0); Translate(-2. 0, 0. 0); draw. Triangle(); Translate(-2. 0, 0. 0); Scale(2. 0, 2. 0); draw. Triangle(); In general, transformations are not commutative

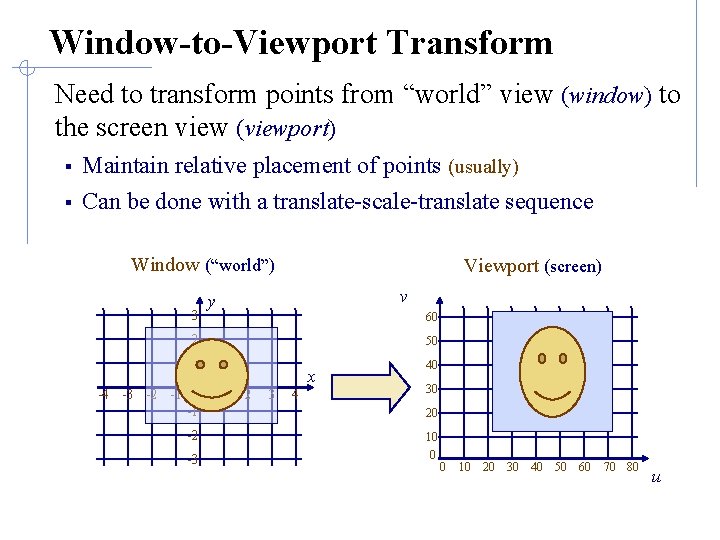
Window-to-Viewport Transform Need to transform points from “world” view (window) to the screen view (viewport) § Maintain relative placement of points (usually) § Can be done with a translate-scale-translate sequence Window (“world”) 3 Viewport (screen) v y 60 2 50 1 -4 -3 -2 -1 0 -1 x 1 2 3 4 40 30 20 -2 10 -3 0 0 10 20 30 40 50 60 70 80 u

Window • “Window” refers to the area in “world space” or “world coordinates” that you wish to project onto the screen • Location, units, size, etc. are all determined by the application, and are convenient for that application • Units could be inches, feet, meters, kilometers, light years, etc. • The window is often centered around the origin, but need not be • Specified as (x, y) coordinates Window (“world”) 3 y (xmax, ymax) 2 1 -4 -3 -2 -1 0 -1 (xmin, ymin) -2 -3 x 1 2 3 4

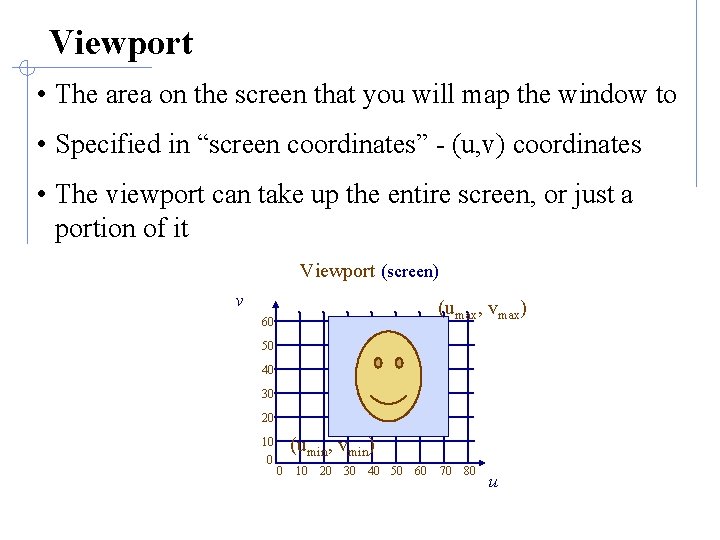
Viewport • The area on the screen that you will map the window to • Specified in “screen coordinates” - (u, v) coordinates • The viewport can take up the entire screen, or just a portion of it Viewport (screen) v (umax, vmax) 60 50 40 30 20 (umin, vmin) 10 0 0 10 20 30 40 50 60 70 80 u

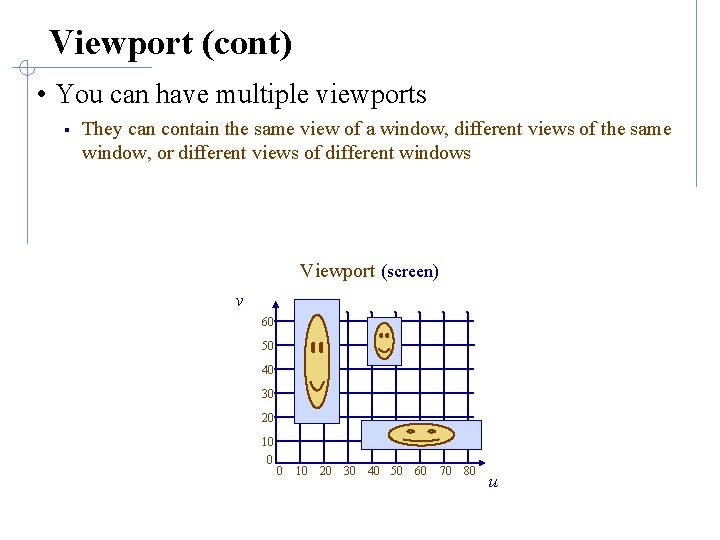
Viewport (cont) • You can have multiple viewports § They can contain the same view of a window, different views of the same window, or different views of different windows Viewport (screen) v 60 50 40 30 20 10 0 0 10 20 30 40 50 60 70 80 u

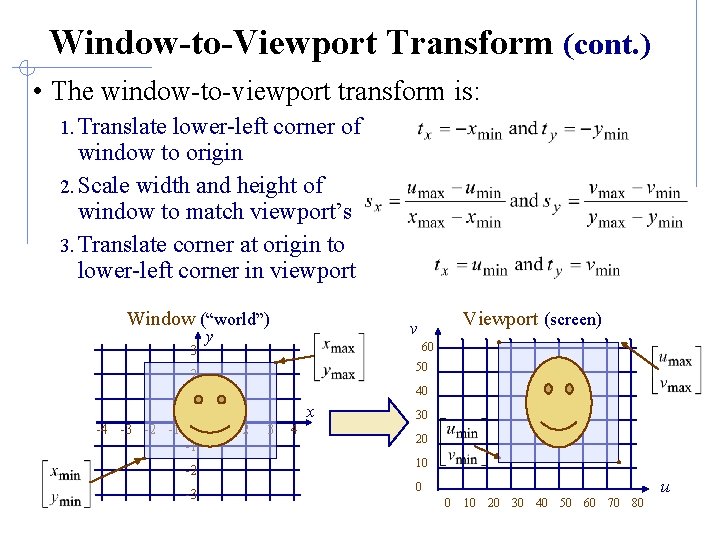
Window-to-Viewport Transform (cont. ) • The window-to-viewport transform is: 1. Translate lower-left corner of window to origin 2. Scale width and height of window to match viewport’s 3. Translate corner at origin to lower-left corner in viewport Window (“world”) 3 Viewport (screen) v y 60 2 50 1 40 -4 -3 -2 -1 0 -1 x 1 2 3 4 30 20 -2 10 -3 0 u 0 10 20 30 40 50 60 70 80

Window-to-Viewport Transform (cont. ) • The final window-to-viewport transform is:

Window-to-Viewport Transform (cont. ) • Multiplying the matrix Mwv by the point p gives:

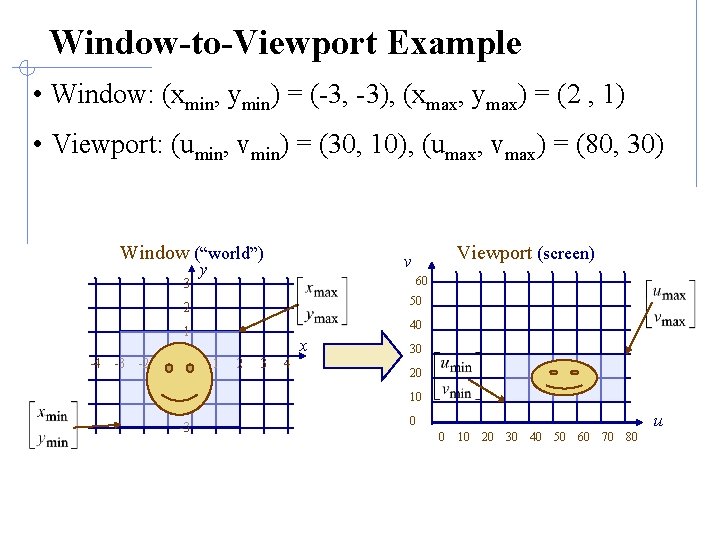
Window-to-Viewport Example • Window: (xmin, ymin) = (-3, -3), (xmax, ymax) = (2 , 1) • Viewport: (umin, vmin) = (30, 10), (umax, vmax) = (80, 30) Window (“world”) 3 Viewport (screen) v y 60 2 50 1 40 -4 -3 -2 -1 0 -1 x 1 2 3 4 30 20 -2 10 -3 0 u 0 10 20 30 40 50 60 70 80

Window-to-Viewport Example • Plugging the values into the equation: Window (“world”) 3 Viewport (screen) v y 60 2 50 1 40 -4 -3 -2 -1 0 -1 x 1 2 3 4 30 20 -2 10 -3 0 u 0 10 20 30 40 50 60 70 80

Window-to-Viewport Example • Plugging the values into the equation:

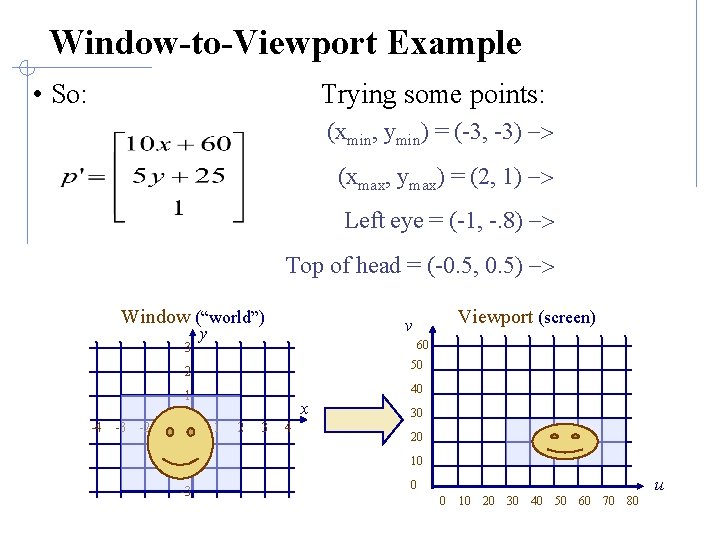
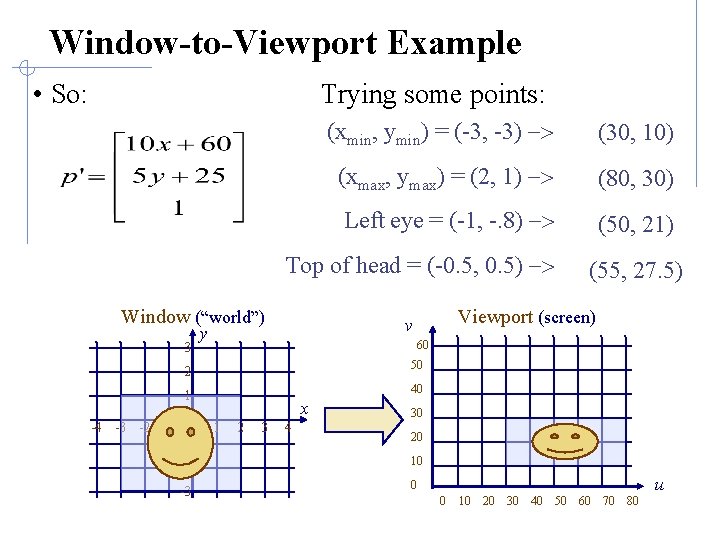
Window-to-Viewport Example • So: Trying some points: (xmin, ymin) = (-3, -3) -> (xmax, ymax) = (2, 1) -> Left eye = (-1, -. 8) -> Top of head = (-0. 5, 0. 5) -> Window (“world”) 3 Viewport (screen) v y 60 2 50 1 40 -4 -3 -2 -1 0 -1 x 1 2 3 4 30 20 -2 10 -3 0 u 0 10 20 30 40 50 60 70 80

Window-to-Viewport Example • So: Trying some points: (xmin, ymin) = (-3, -3) -> (30, 10) (xmax, ymax) = (2, 1) -> (80, 30) Left eye = (-1, -. 8) -> (50, 21) Top of head = (-0. 5, 0. 5) -> Window (“world”) 3 Viewport (screen) v y 60 2 50 1 40 -4 -3 -2 -1 0 -1 (55, 27. 5) x 1 2 3 4 30 20 -2 10 -3 0 u 0 10 20 30 40 50 60 70 80

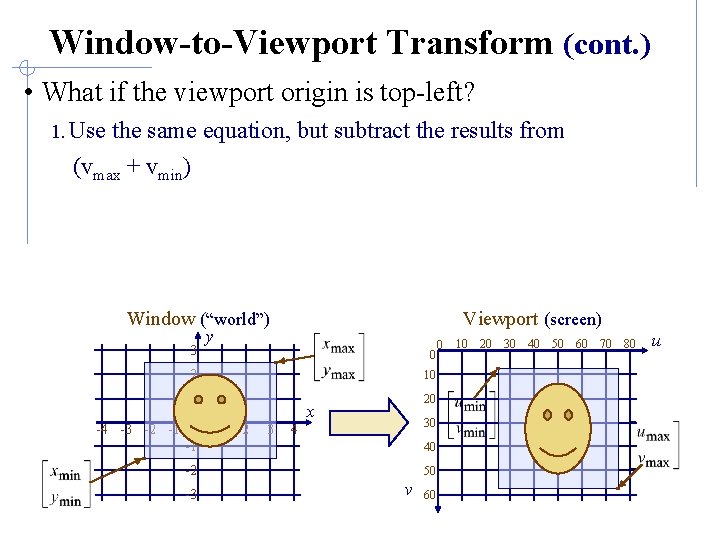
Window-to-Viewport Transform (cont. ) • What if the viewport origin is top-left? 1. Use the same equation, but subtract the results from (vmax + vmin) Window (“world”) 3 Viewport (screen) y 0 2 10 1 20 -4 -3 -2 -1 0 -1 x 1 2 3 30 4 40 -2 -3 50 v 60 0 10 20 30 40 50 60 70 80 u

Window-to-Viewport Transform (cont. ) • Rationale: 1. If vmin = 0, we reverse the results of our equation by subtracting it from vmax, i. e. , vmax -> 0 and 0 -> vmax 2. If we take (vmax - vmin) we get the correct scale factor 3. We need to move the point in question back to the v-axis, then scale 4. We need to add vmin to get from the v-axis back to the original point location, so the scaling is correct Thus, we have (vmax - vmin) - (p - vmin) + vmin = vmax + vmin - p

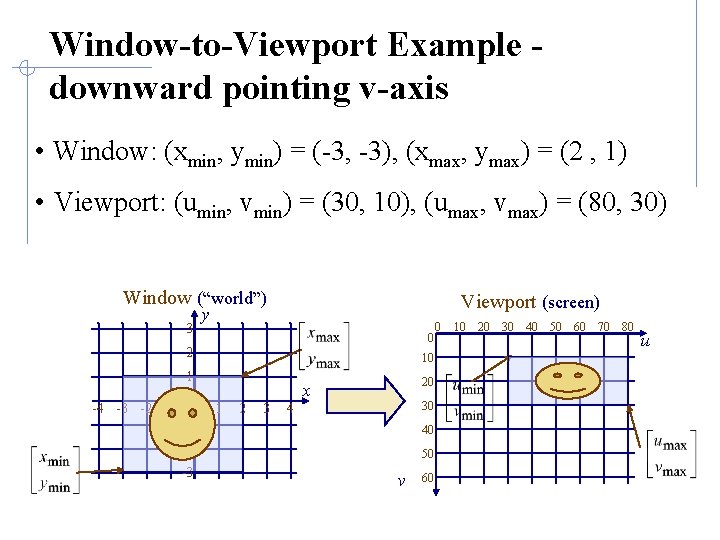
Window-to-Viewport Example downward pointing v-axis • Window: (xmin, ymin) = (-3, -3), (xmax, ymax) = (2 , 1) • Viewport: (umin, vmin) = (30, 10), (umax, vmax) = (80, 30) Window (“world”) 3 Viewport (screen) y 0 2 10 1 -4 -3 -2 -1 0 -1 20 x 1 2 3 30 4 40 -2 -3 50 v 60 0 10 20 30 40 50 60 70 80 u

Window-to-Viewport Example downward pointing v-axis • The equation for this situation is:

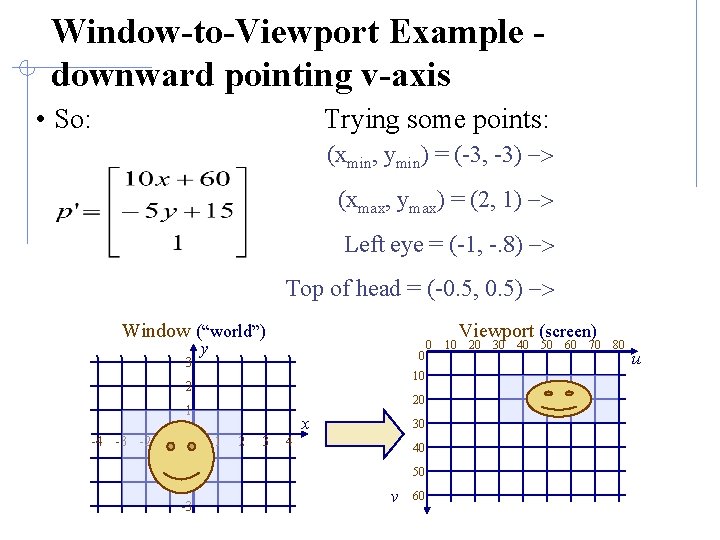
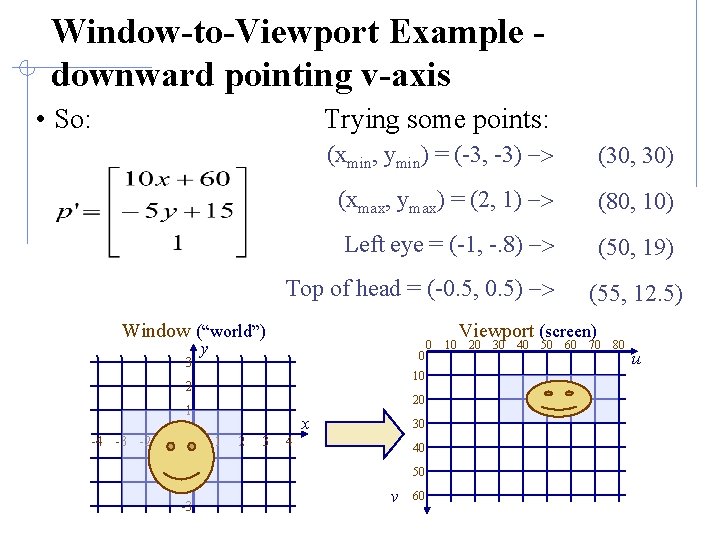
Window-to-Viewport Example downward pointing v-axis • So: Trying some points: (xmin, ymin) = (-3, -3) -> (xmax, ymax) = (2, 1) -> Left eye = (-1, -. 8) -> Top of head = (-0. 5, 0. 5) -> Window (“world”) 3 y 0 10 2 20 1 -4 -3 -2 -1 0 -1 -2 -3 x 1 2 3 30 4 40 50 v 60 0 10 Viewport (screen) 20 30 40 50 60 70 80 u

Window-to-Viewport Example downward pointing v-axis • So: Trying some points: (xmin, ymin) = (-3, -3) -> (30, 30) (xmax, ymax) = (2, 1) -> (80, 10) Left eye = (-1, -. 8) -> (50, 19) Top of head = (-0. 5, 0. 5) -> Window (“world”) 3 y 0 10 2 20 1 -4 -3 -2 -1 0 -1 -2 -3 x 1 2 3 30 4 40 50 v 60 0 10 (55, 12. 5) Viewport (screen) 20 30 40 50 60 70 80 u