CS 447 Computer Architecture Lecture 3 Computer Arithmetic

CS 447 – Computer Architecture Lecture 3 Computer Arithmetic (2) September 5, 2007 Karem Sakallah ksakalla@qatar. cmu. edu www. qatar. cmu. edu/~msakr/15447 -f 07/ Computer Architecture Fall 2007 ©

Last Time ° Representation of finite-width unsigned and signed integers ° Addition and subtraction of integers ° Multiplication of unsigned integers Computer Architecture Fall 2007 ©

Today ° Review of multiplication of unsigned integers ° Multiplication of signed integers ° Division of unsigned integers ° Representation of real numbers ° Addition, subtraction, multiplication, and division of real numbers Computer Architecture Fall 2007 ©

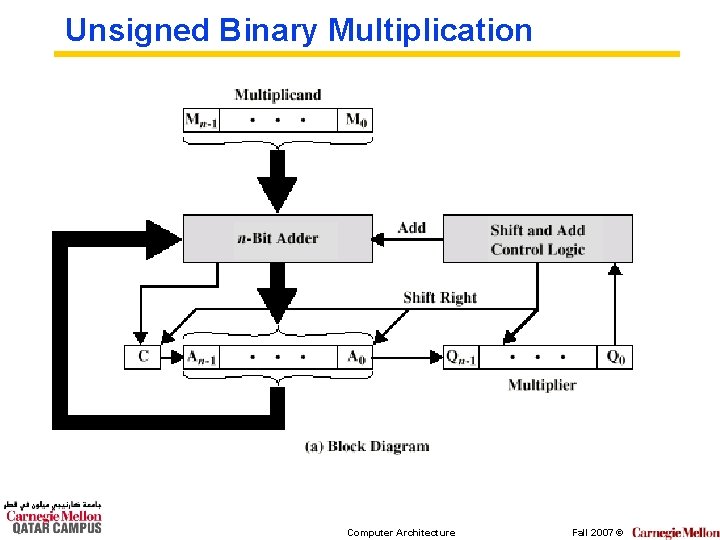
Multiplication ° Complex ° Work out partial product for each digit ° Take care with place value (column) ° Add partial products Computer Architecture Fall 2007 ©

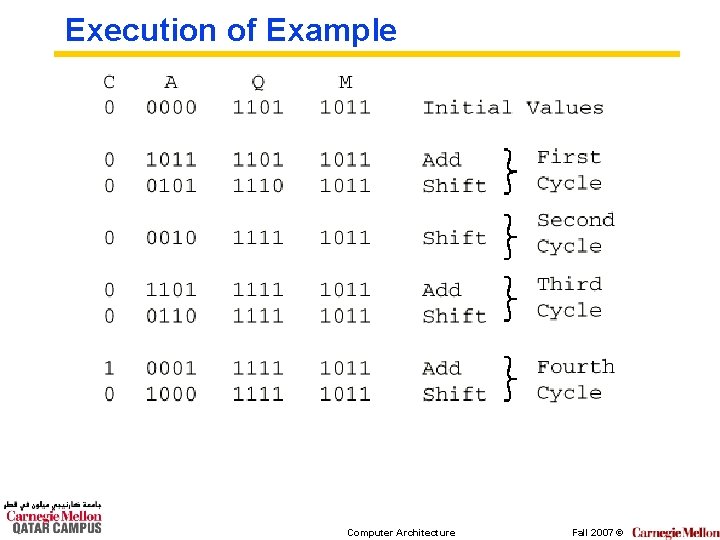
Multiplication Example ° ° 1011 Multiplicand (11 dec) x 1101 Multiplier (13 dec) 1011 Partial products 0000 Note: if multiplier bit is 1 copy ° 1011 multiplicand (place value) ° 1011 otherwise zero ° 10001111 Product (143 dec) ° Note: need double length result Computer Architecture Fall 2007 ©

Unsigned Binary Multiplication Computer Architecture Fall 2007 ©

Execution of Example Computer Architecture Fall 2007 ©

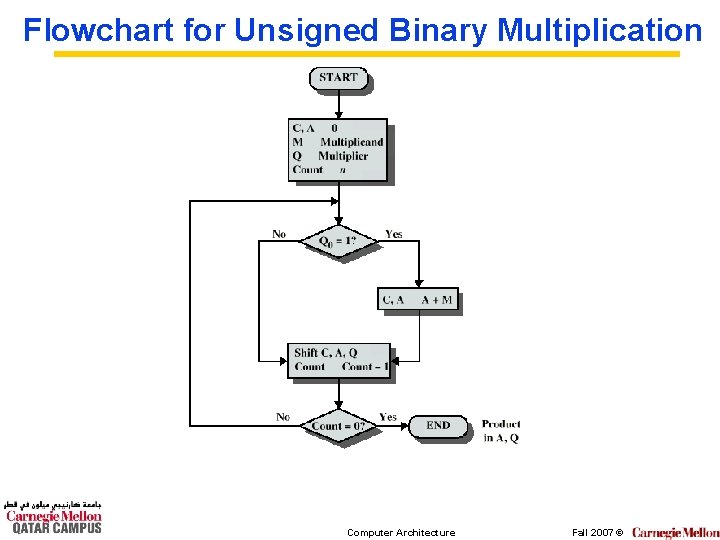
Flowchart for Unsigned Binary Multiplication Computer Architecture Fall 2007 ©

Multiplying Negative Numbers ° This does not work! ° Solution 1 • Convert to positive if required • Multiply as above • If signs were different, negate answer ° Solution 2 • Booth’s algorithm Computer Architecture Fall 2007 ©

Observation ° Which of these two multiplications is more difficult? 98, 765 x 10, 001 98, 765 x 9, 999 ° Note: 98, 765 x 10, 001 = 98, 765 x (10, 000 + 1) 98, 765 x 9, 999 = 98, 765 x (10, 000 – 1) Computer Architecture Fall 2007 ©

In Binary Let Q = d d d 0 1 1. . . 1 1 0 d d QL = d d d 1 0 0. . . 0 0 0 d d QR = 0 0 0. . . 0 1 0 0 0 Computer Architecture Fall 2007 ©

In Binary Let Q = d d d 0 1 1. . . 1 1 0 d d QL = d d d 1 0 0. . . 0 0 0 d d QR = 0 0 0. . . 0 1 0 0 0 Then Q = QL – QR And M x Q = M x QL – M x QR Computer Architecture Fall 2007 ©

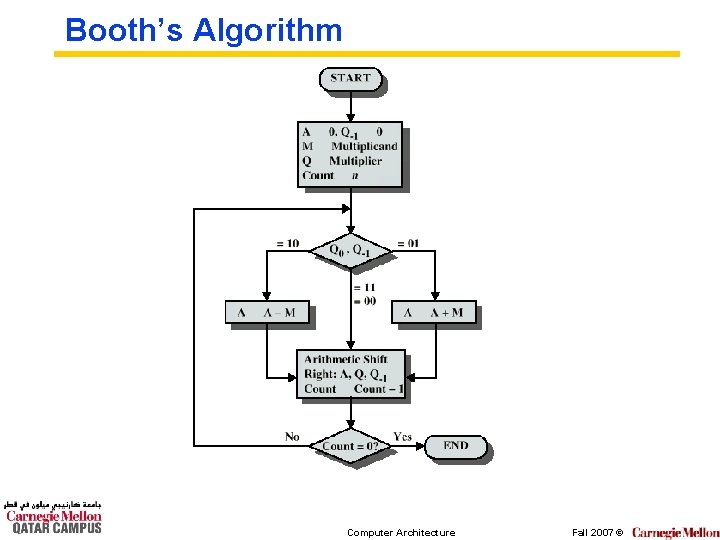
A bit more explanation P=Mx. Q where M and Q are n-bit two’s complement integers e. g. , Q = -23 q 3 + 22 q 2 + 21 q 1 + 20 q 0 which can be re-written as follows: Q = 20(q-1–q 0)+21(q 0 -q 1)+22(q 1 -q 2)+23(q 2 -q 3) leading to P= M x 20 x (q-1 - q 0) + M x 21 x (q 0 - q 1) + M x 22 x (q 1 - q 2) + M x 23 x (q 2 - q 3) Computer Architecture Fall 2007 ©

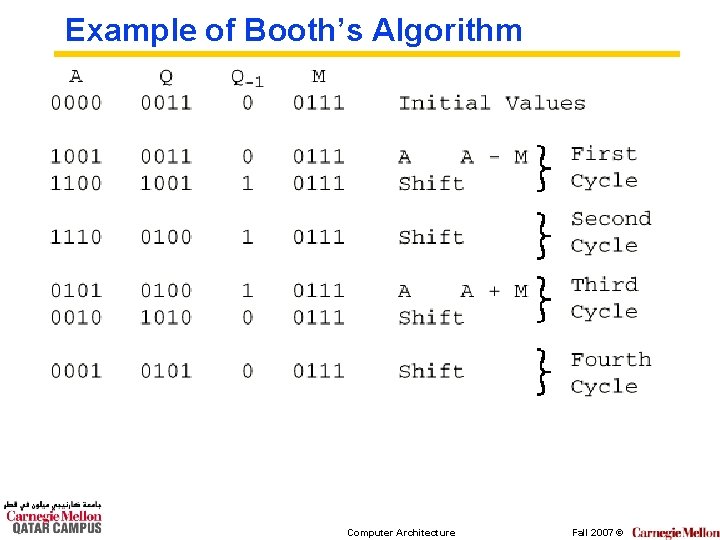
Finally! P= M x 20 x (q-1 - q 0) + M x 21 x (q 0 - q 1) + M x 22 x (q 1 - q 2) + M x 23 x (q 2 - q 3) qi qi-1 – qi Action 0 0 0 Noop 0 1 1 Add M 1 0 -1 Subtract M 1 1 0 Noop Computer Architecture Fall 2007 ©

Example of Booth’s Algorithm Computer Architecture Fall 2007 ©

Booth’s Algorithm Computer Architecture Fall 2007 ©

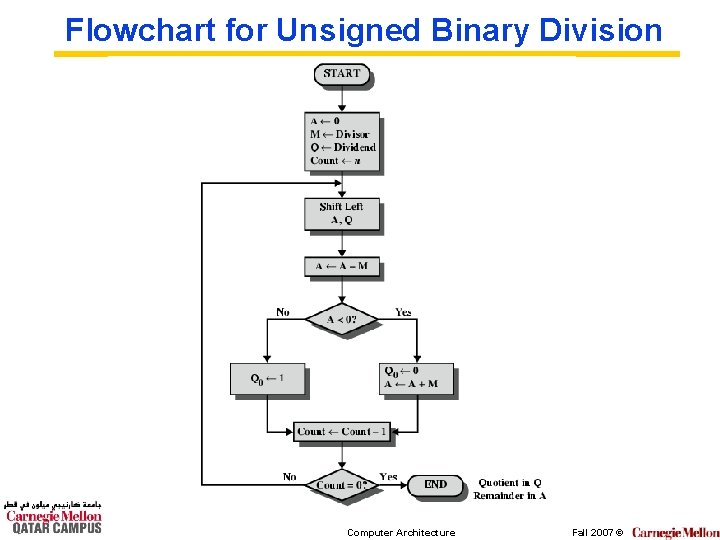
Division ° More complex than multiplication ° Negative numbers are really bad! ° Based on long division Computer Architecture Fall 2007 ©

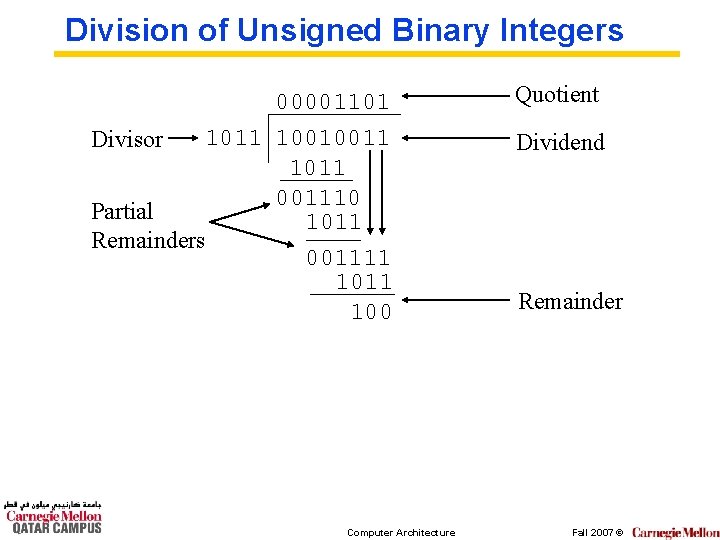
Division of Unsigned Binary Integers 00001101 1011 10010011 Divisor 1011 001110 Partial 1011 Remainders 001111 100 Computer Architecture Quotient Dividend Remainder Fall 2007 ©

Flowchart for Unsigned Binary Division Computer Architecture Fall 2007 ©

Real Numbers ° Numbers with fractions ° Could be done in pure binary • 1001. 1010 = 24 + 20 +2 -1 + 2 -3 =9. 625 ° Where is the binary point? ° Fixed? • Very limited ° Moving? • How do you show where it is? Computer Architecture Fall 2007 ©

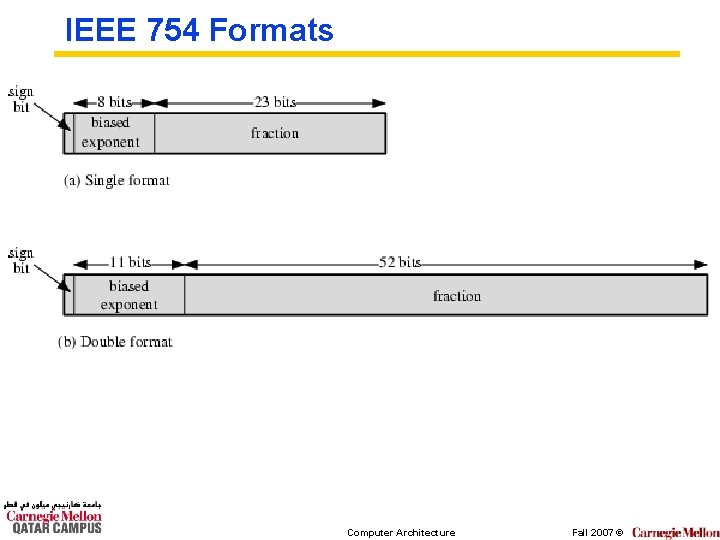
Sign bit Floating Point Biased Exponent Significand or Mantissa ° +/-. significand x 2 exponent ° Misnomer ° Point is actually fixed between sign bit and body of mantissa ° Exponent indicates place value (point position) Computer Architecture Fall 2007 ©

Floating Point Examples Computer Architecture Fall 2007 ©

Signs for Floating Point ° Mantissa is stored in two’s complement ° Exponent is in excess or biased notation • e. g. Excess (bias) 128 means • 8 bit exponent field • Pure value range 0 -255 • Subtract 128 to get correct value • Range -128 to +127 Computer Architecture Fall 2007 ©

Normalization ° FP numbers are usually normalized ° i. e. exponent is adjusted so that leading bit (MSB) of mantissa is 1 ° Since it is always 1 there is no need to store it ° (c. f. Scientific notation where numbers are normalized to give a single digit before the decimal point ° e. g. 3. 123 x 103) Computer Architecture Fall 2007 ©

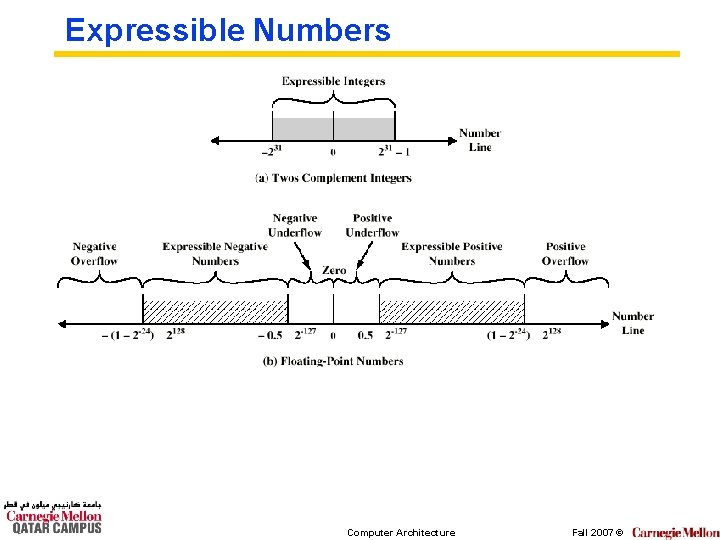
FP Ranges ° For a 32 bit number • 8 bit exponent • +/- 2256 1. 5 x 1077 ° Accuracy • The effect of changing lsb of mantissa • 23 bit mantissa 2 -23 1. 2 x 10 -7 • About 6 decimal places Computer Architecture Fall 2007 ©

Expressible Numbers Computer Architecture Fall 2007 ©

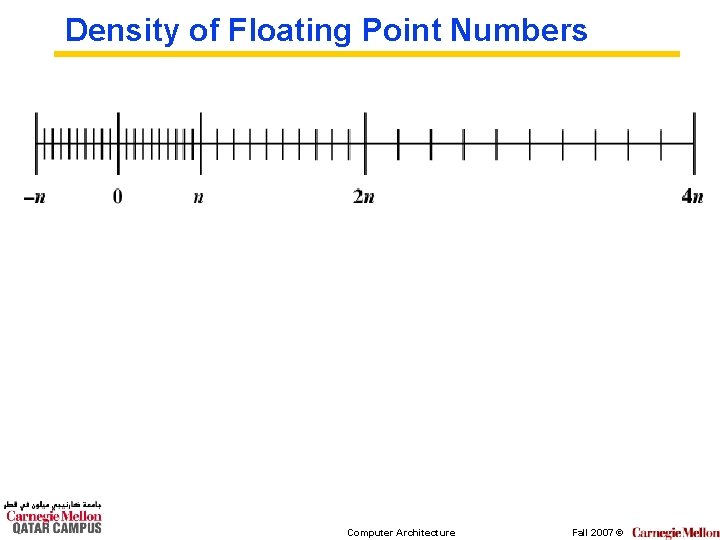
Density of Floating Point Numbers Computer Architecture Fall 2007 ©

IEEE 754 Formats Computer Architecture Fall 2007 ©

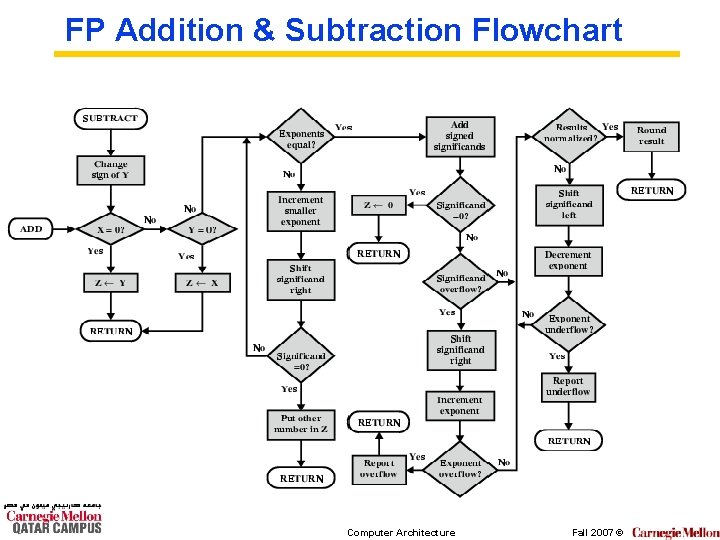
FP Arithmetic +/- ° Check for zeros ° Align significands (adjusting exponents) ° Add or subtract significands ° Normalize result Computer Architecture Fall 2007 ©

FP Addition & Subtraction Flowchart Computer Architecture Fall 2007 ©

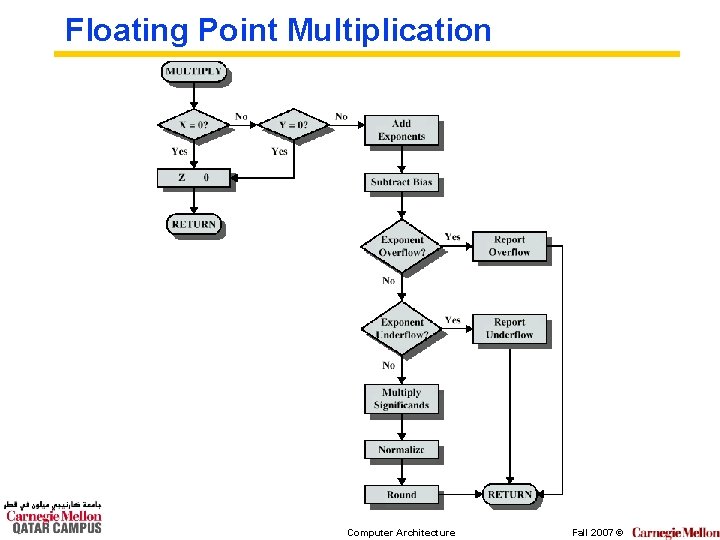
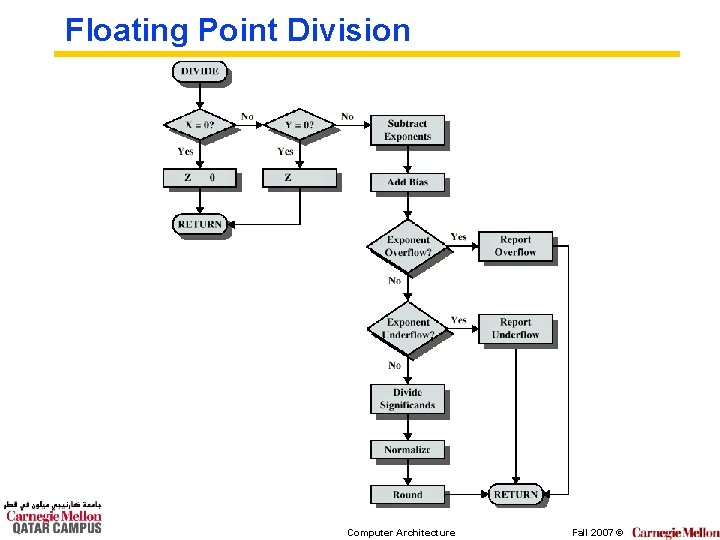
FP Arithmetic x/ ° Check for zero ° Add/subtract exponents ° Multiply/divide significands (watch sign) ° Normalize ° Round ° All intermediate results should be in double length storage Computer Architecture Fall 2007 ©

Floating Point Multiplication Computer Architecture Fall 2007 ©

Floating Point Division Computer Architecture Fall 2007 ©