CS 4433 Database Systems Relational Algebra Why Do

CS 4433 Database Systems Relational Algebra

Why Do We Learn This? ■ Until now, we learn how to create a database for a domain – Create ER diagram – Convert ER to Relational Model – Write SQL to create tables for relations in our RM ■ Now, Querying the database: specify what we want from our database – Find all the people who earn more than $1, 000 and pay taxes in Oklahoma

Why Do We Learn This? ■ In SQL we write WHAT we want to get from the data ■ The database system needs to figure out HOW to get the data we want ■ The passage from WHAT to HOW goes through the Relational Algebra ■ Querying the database: specify what we want from our database – – 3 Find all the people who earn more than $1, 000 and pay taxes in Oklahoma ■ Could write in C++/Java, but a bad idea ■ Instead use high-level query languages: – Theoretical: Relational Algebra – Practical: SQL Relational algebra: a basic set of operations on relations that provide the basic principles

What is an “Algebra”? ■ ■ Mathematical system consisting of: – Operands --- variables or values from which new values can be constructed – Operators --- symbols denoting procedures that construct new values from given values Examples – Arithmetic(Elementary) algebra, linear algebra, Boolean algebra …… ■ What are operands? – ■ What are operators? – 4 Arithmetic Algebra: variables like x and constants like 15 Arithmetic Algebra: addition, subtraction…

What is Relational Algebra? ■ An algebra – Whose operands are relations or variables that represent relations – Whose operators are designed to do common things that we need to do with relations in a database ■ relations as input, new relation as output – Can be used as a query language for relations! 5

Relational Operators ■ Five basic RA operations: – Basic Set Operations ■ ■ ■ Difference Union Selection: (s) eliminates some rows of relations Projection: (p) eliminates some columns of relations Cartesian Product: (X) combine the tuples of two relations ■ When our relations have attribute names: – Renaming: (r) change the relation schema ■ Derived operations: – Intersection, complement – Joins (natural join, equi-join, theta join, semi-join, ……) 6

Selection ■ Applied to a relation R, produce a new relation with a subset of R’s tuples ■ Returns all tuples (rows) which satisfy a condition that involves the attributes of R, denoted as sc(R) – c is a condition: a Boolean combination of terms – Term is one the following forms: 1. 2. 3. 4. attribute op constant attribute 1 op attribute 2 term 1 ∧ term 2 term 1 ∨ term 2 – operators {=, <, >, ≤, ≥, ≠, AND, OR, NOT} – Output schema: same as input schema 7

Example – Find all employees with salary more than $40, 000: ■ s. Salary > 40000 (Employee) SSN Name Dept-ID Salary 111060000 Alex 1 30 K 754320032 Bob 1 32 K 983210129 Chris 2 45 K SSN 98321012 9 Name Dept-ID Salary Chris 2 45 K

Projection ■ Applied to a relation R, produce a new relation with a subset of R’s columns ■ Unary operation: returns certain columns, denoted as P A 1, …, An (R) – Eliminates duplicate tuples ! ■ since relations are sets – Input schema R(B 1, …, Bm) – Condition: {A 1, …, An} {B 1, …, Bm} – Output schema S(A 1, …, An) 9

Example ■ Get social-security number and names of all Employees ■ P SSN, Name (Employee) SSN Name Dept-ID Salary SSN Name 111060000 Alex 1 30 K 111060000 Alex 754320032 Bob 1 32 K 754320032 Bob 983210129 Chris 2 45 K 983210129 Chris

Selection vs. Projection ■ Think of relation as a table – How are they similar? ■ Selection of subsets from table – How are they different? ■ Horizontal vs. vertical? – ■ Duplicate elimination for both? – 11 selection-projection No duplicate in the result of selection

Set Operations - Union ■ all tuples in R 1 or R 2, denoted as R 1 U R 2 – R 1, R 2 must have the same schema – R 1 U R 2 has the same schema as R 1, R 2 – Example: ■ Active-Employees U Retired-Employees – If any, is duplicate elimination required? ■ yes R 1 U R 2 R 1 12 R 2 SSN Name 111060000 Alex 754320032 Bob 983210129 Chris 346565223 Alice 983210129 Chris

Set Operations - Difference: ■ all tuples in R 1 but not in R 2, denoted as R 1 – R 2 – R 1, R 2 must have the same schema – R 1 - R 2 has the same schema as R 1, R 2 – Example ■ All-Employees - Retired-Employees R 1 R 2 SSN Name 111060000 Alex SSN Name 754320032 Bob 983210129 Chris 346565223 Alice 983210129 Chris R 1 - R 2

Set Operations: Intersection ■ Intersection: all tuples both in R 1 and in R 2, denoted as R 1 R 2 – R 1, R 2 must have the same schema – R 1 R 2 has the same schema as R 1, R 2 – Example: Active. Employees ■ Intersection ( R 1 Retired. Employees R 2 ) is derived: why ? – = R 1 – (R 1 – R 2) R 1 14 R 2 SSN Name 111060000 Alex 754320032 Bob 983210129 Chris 346565223 Alice R 1 ∩ R 2 SSN Name 111060000 Alex 754320032 Bob

Cartesian Product ■ Combine each tuple in R 1 with each tuple in R 2, denoted as R 1 x R 2 – Input schemas R 1(A 1, …, An), R 2(B 1, …, Bm) – Output schema is S(A 1, …, An, B 1, …, Bm) ■ Two relations are combined! – Very rare in practice; but joins are very common – Example: Employee x Dependent 15

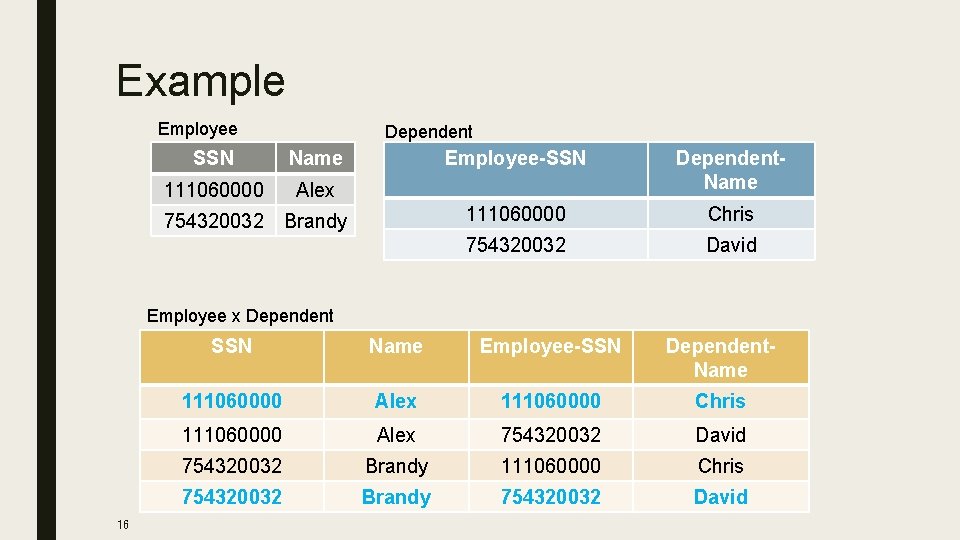
Example Employee Dependent SSN Name 111060000 Alex 754320032 Brandy Employee-SSN Dependent. Name 111060000 Chris 754320032 David Employee x Dependent 16 SSN Name Employee-SSN Dependent. Name 111060000 Alex 111060000 Chris 111060000 Alex 754320032 David 754320032 Brandy 111060000 Chris 754320032 Brandy 754320032 David

Renaming ■ Does not change the relational instance, denoted as Notation: r S(B 1, …, Bn) (R) ■ Changes the relational schema only – Input schema: R(A 1, …, An) – Output schema: S(B 1, …, Bn) ■ Example: r Soc-sec-num, firstname(Employee) 17 SSN Name Soc-sec-num firstname 111060000 Alex 754320032 Bob 983210129 Chris

Theta Join ■ A join that forces us to pair tuples using one specific condition – involves a predicate q, denoted as R 1 q R 2 – Input schemas: R 1(A 1, …, An), R 2(B 1, …, Bm) – Output schema: S(A 1, …, An, B 1, …, Bm) – Derived operator: R 1 q R 2 = s q (R 1 x R 2) 1. Take the (Cartisian) product R 1 x R 2 2. Then apply SELECTC to the result – As for SELECT, C can be any Boolean-valued condition 18

Equi-join ■ Special case of theta join: condition c contains only conjunctions of equalities – Result schema is the same as that of Cartesian product – May have fewer tuples than Cartesian product – Most frequently used in practice: R 1 19 A=B R 2

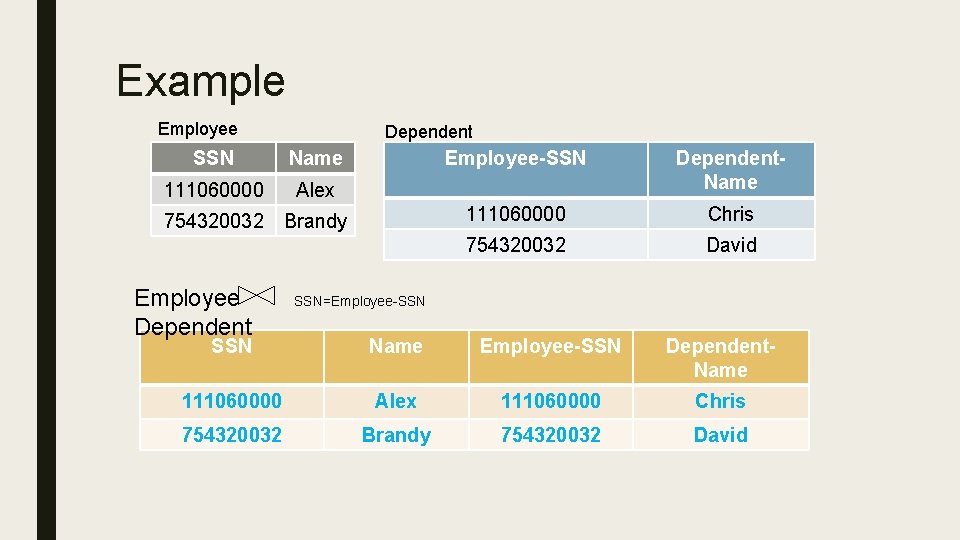
Example Employee Dependent SSN Name 111060000 Alex 754320032 Brandy Employee SSN=Employee-SSN Dependent. Name 111060000 Chris 754320032 David SSN Name Employee-SSN Dependent. Name 111060000 Alex 111060000 Chris 754320032 Brandy 754320032 David

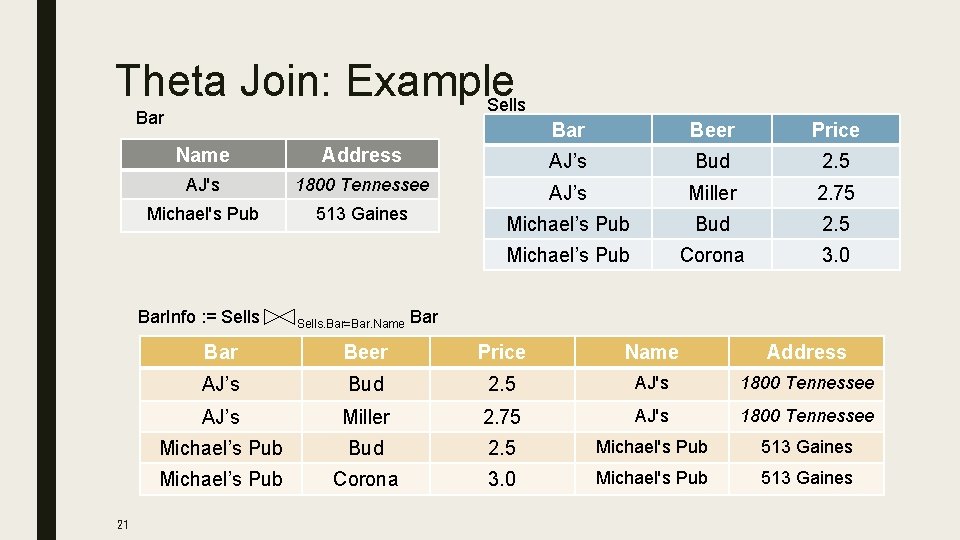
Theta Join: Example Sells Bar Beer Price Name Address AJ’s Bud 2. 5 AJ's 1800 Tennessee AJ’s Miller 2. 75 Michael's Pub 513 Gaines Michael’s Pub Bud 2. 5 Michael’s Pub Corona 3. 0 Bar. Info : = Sells. Bar=Bar. Name Bar 21 Bar Beer Price Name Address AJ’s Bud 2. 5 AJ's 1800 Tennessee AJ’s Miller 2. 75 AJ's 1800 Tennessee Michael’s Pub Bud 2. 5 Michael's Pub 513 Gaines Michael’s Pub Corona 3. 0 Michael's Pub 513 Gaines

Natural Join Notation: R 1 R 2= P L (s q (R 1 x R 2)) ■ L is the list of attributes in R and in S that are also not in R ■ Input Schema: R 1(A 1, …, An), R 2(B 1, …, Bm) ■ Output Schema: S(C 1, …, Cp) – Where {C 1, …, Cp} = {A 1, …, An} U{B 1, …, Bm} ■ Meaning: combine all pairs of tuples in R 1 and R 2 that agree on the join attributes: – {A 1, …, An} {B 1, …, Bm} (common attributes in both the schema of R 1 and R 2 called the join attributes) ■ Natural join is a particular case of equi-join ■ A lot of research on how to do it efficiently 22

Natural Join: Examples Employee Dependent SSN Name 111060000 Alex 754320032 Brandy SSN Dependent. Name 111060000 Chris 754320032 David Employee Dependent = P SSN, Name, Dependent-Name(s. Employee. SSN=Dependent. SSN(Employee x Dependent) 23 SSN Name Dependent. Name 111060000 Alex Chris 754320032 Brandy David

Natural Join: Examples R S A B B C X Y Z U X Z V W Y Z Z V R S 24 A B C X Z U X Z V Y Z U Y Z V W

So Which Join Is It ? ■ When we write R � S we usually mean an eq-join, but we often omit the equality predicate when it is clear from the context ■ The join operation in all its variants (eqjoin, natural join, semi-join, outer-join) is at the heart of relational database systems

Building Complex Expressions ■ Algebras allow us to express sequences of operations in a natural way – Example ■ In arithmetic algebra: (x + 4)*(y - 3) – Relational algebra allows the same ■ Three notations, just as in arithmetic: 1. Sequences of assignment statements 2. Expressions with several operators 3. Expression trees 26

Sequences of Assignments ■ Create temporary relation names ■ Renaming can be implied by giving relations a list of attributes ■ Example: R 3 : = R 1 C R 2 can be written: R 4 : = R 1 x R 2 (R 4: temporary relation) R 3 : = s. C (R 4) 27

Expressions with Several Operators ■ Example: theta-join R 3 : = R 1 JOINC R 2 can be written: R 3 : = s. C (R 1 x R 2) ■ Precedence of relational operators: 1. Unary operators --- select, project, rename --- have highest precedence, bind first 2. Then cartesian products and joins 3. Then intersection 4. Finally, union and set difference bind last ■ But you can always insert parentheses to force the order you desire 28

Expression Trees ■ Leaves are operands – either variables standing for relations or particular constant relations ■ Interior nodes are operators, applied to their child or children 29

Expression Tree: Examples Given Company(name, address), Sells(company, product, price), find the names of all the company that are either on Monroe St. or sell Book for less than $3 U r R(name) P name saddress = “Monroe St. ” Campany 30 P Product s price<3 AND product=“Book” Sells

Relational Algebra as a Constraint Language ■ Two ways to express constraints. – If R is an expression of relational algebra, then R=∅ is a constraint that says ”The value of R must be empty, ” or equivalently ”There are no tuples in the result of R”. – If R and S are expressions of relational algebra, then R ⊆ S is a constraint that says ”Every tuple in the result of R must also in the result of S. ” Of course the result of S may contain additional tuples not produced by R.

Referential Integrity Constraints ■

Key Constraints ■

Additional Constraints ■

Division Operator (÷) ■ Attributes of B is proper subset of Attributes of A. ■ The relation returned by division operator will have attributes = (All attributes of A – All Attributes of B) ■ The relation returned by division operator will return those tuples from relation A which are associated to every B’s tuple.

Examples ■ EMP(ssn, name, gender, salary) ■ Emp_proj(essn, pnumber, hours)

■ EMP(ssn, name, gender, salary) ■ Emp_proj(essn, pnumber, hours)

EMP(ssn, name, gender, salary) Emp_proj(essn, pnumber, hours)

EMP(ssn, name, gender, salary) Emp_proj(essn, pnumber, hours

Relational Algebra ■ RA = Dataflow Program ■ Several operations, plus strictly specified order ■ In RDBMS the dataflow graph is always a tree