CS 430585 Computer Graphics I 3 D Representation

CS 430/585 Computer Graphics I 3 D Representation and Solid Modeling Week 8, Lecture 16 David Breen, William Regli and Maxim Peysakhov Geometric and Intelligent Computing Laboratory Department of Computer Science Drexel University http: //gicl. cs. drexel. edu 1

Overview • Implicit solid modeling • 3 D Mesh File Formats • Approximate representations – – Cell decomposition Spatial occupancy enumeration Quad and oct trees Binary space partition trees • Statistical representations 2 1994 Foley/Van. Dam/Finer/Huges/Phillips ICG

Implicit Solid Modeling • Computer Algebra meets CAD • Idea: – Represents solid as the set of points where an implicit global function takes on certain value • F(x, y, z) < val – Primitive solids are combined using CSG – Composition operations are implemented by functionals which provide an implicit function for the resulting solid 3 From M. Ganter, D. Storti, G. Turkiyyah @ UW

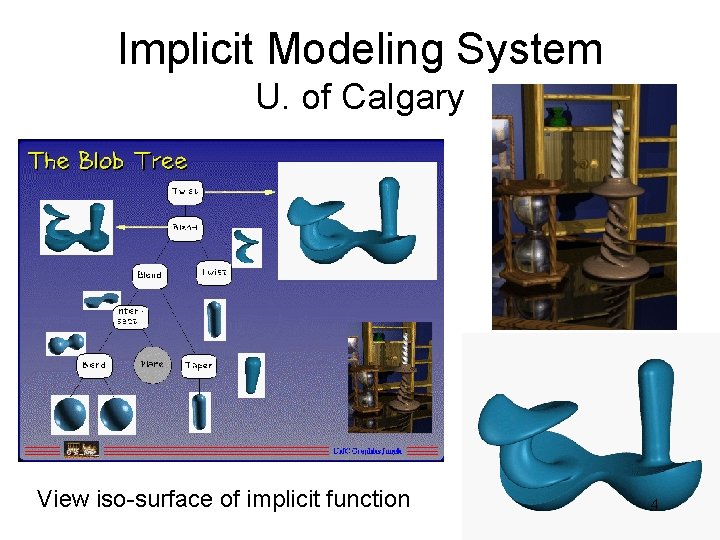
Implicit Modeling System U. of Calgary View iso-surface of implicit function 4

Implicit Modeling System U. of Calgary 5

Approximate Representations • Idea: discretize the world! • Surface Models – Mesh, facet and polygon representations • Volume Models – spatial enumeration – voxelization 6

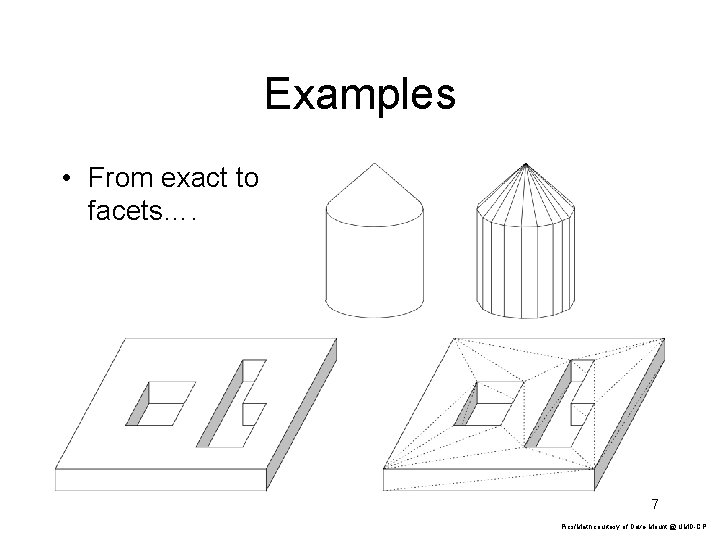
Examples • From exact to facets…. 7 Pics/Math courtesy of Dave Mount @ UMD-CP

3 D Mesh File Formats Some common formats • STL • SMF • Open. Inventor • VRML 8

Minimal • Vertex + Face • No colors, normals, or texture • Primarily used to demonstrate geometry algorithms 9

Full-Featured • Colors / Transparency • Vertex-Face Normals (optional, can be computed) • • Scene Graph Lights Textures Views and Navigation 10

Simple Mesh Format (SMF) • Michael Garland http: //graphics. uiuc. edu/~garland/ • Triangle data • Vertex indices begin at 1 11

Stereolithography (STL) • Triangle data + Face Normal • The de-facto standard for rapid prototyping 12

How STL Works 13

How STL Works 14

Open Inventor • Developed by SGI • Predecessor to VRML – Scene Graph 15

Virtual Reality Modeling Language (VRML) • SGML Based • Scene-Graph • Full Featured 16

Issues with 3 D “mesh” formats • • Easy to acquire Easy to render Harder to model with Error prone – split faces, holes, gaps, etc 17

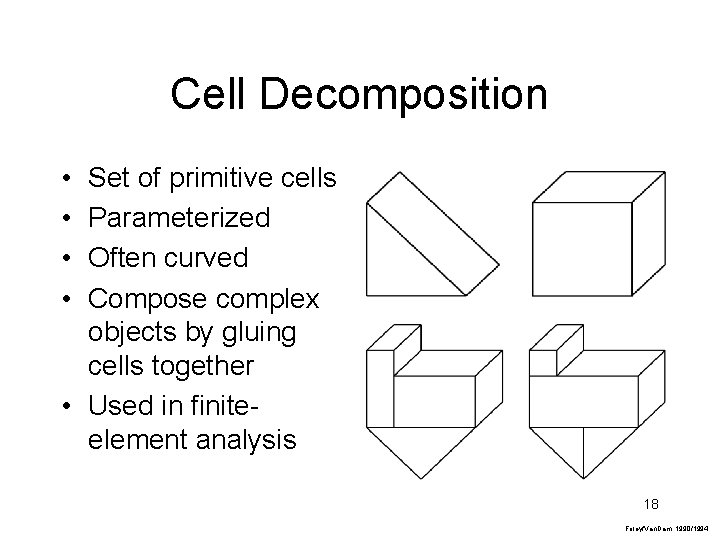
Cell Decomposition • • Set of primitive cells Parameterized Often curved Compose complex objects by gluing cells together • Used in finiteelement analysis 18 Foley/Van. Dam, 1990/1994

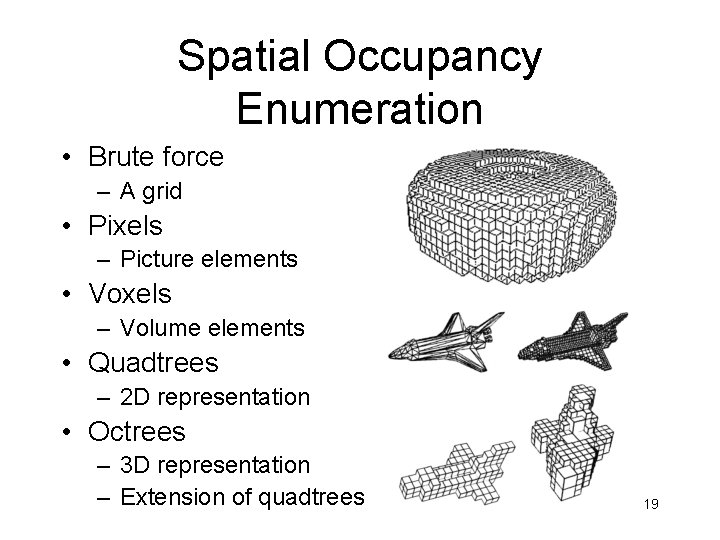
Spatial Occupancy Enumeration • Brute force – A grid • Pixels – Picture elements • Voxels – Volume elements • Quadtrees – 2 D representation • Octrees – 3 D representation – Extension of quadtrees 19

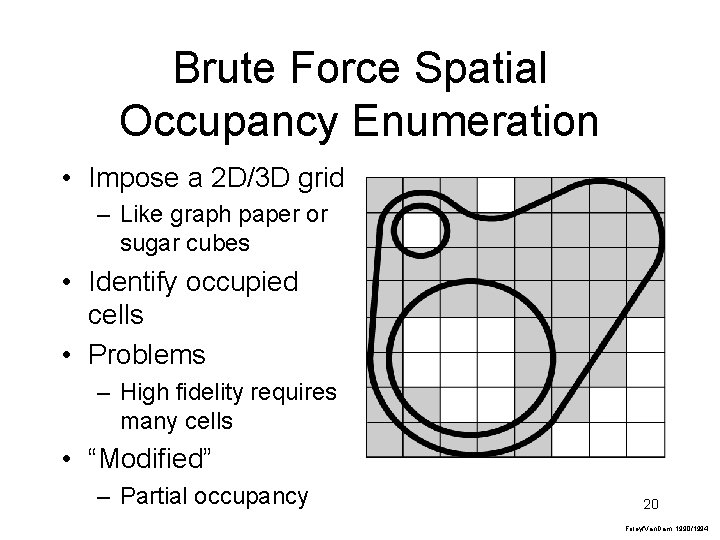
Brute Force Spatial Occupancy Enumeration • Impose a 2 D/3 D grid – Like graph paper or sugar cubes • Identify occupied cells • Problems – High fidelity requires many cells • “Modified” – Partial occupancy 20 Foley/Van. Dam, 1990/1994

Distance Volume • Store signed distance to surface at each voxel Narrow-band representation Iso-surface at value 0 approximates the original surface. 21

Offset Surfaces from Distance Volumes 22

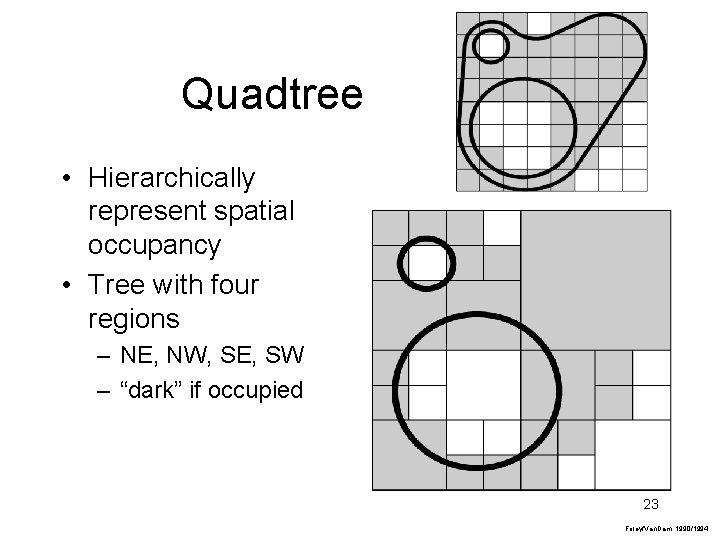
Quadtree • Hierarchically represent spatial occupancy • Tree with four regions – NE, NW, SE, SW – “dark” if occupied 23 Foley/Van. Dam, 1990/1994

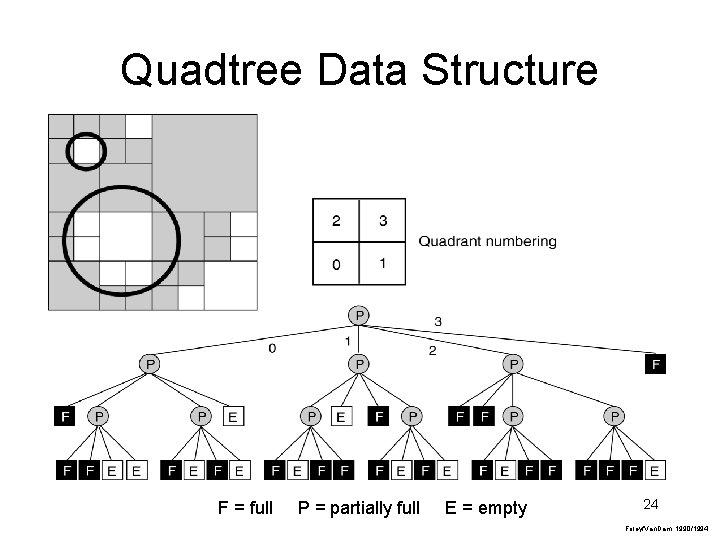
Quadtree Data Structure F = full P = partially full E = empty 24 Foley/Van. Dam, 1990/1994

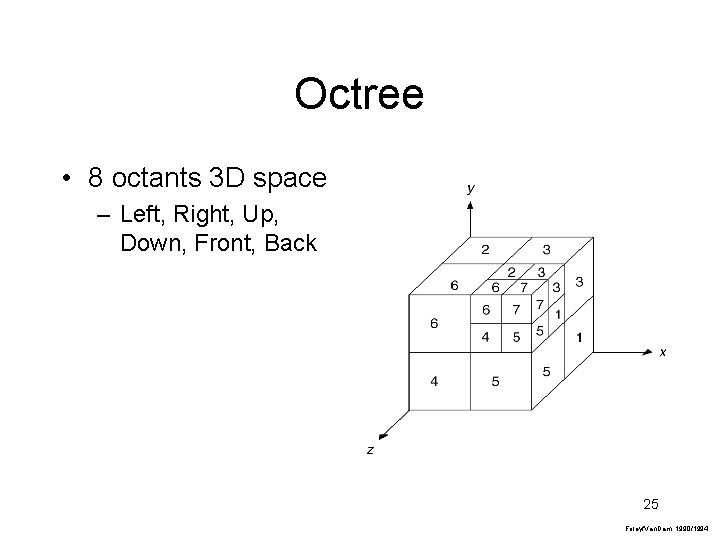
Octree • 8 octants 3 D space – Left, Right, Up, Down, Front, Back 25 Foley/Van. Dam, 1990/1994

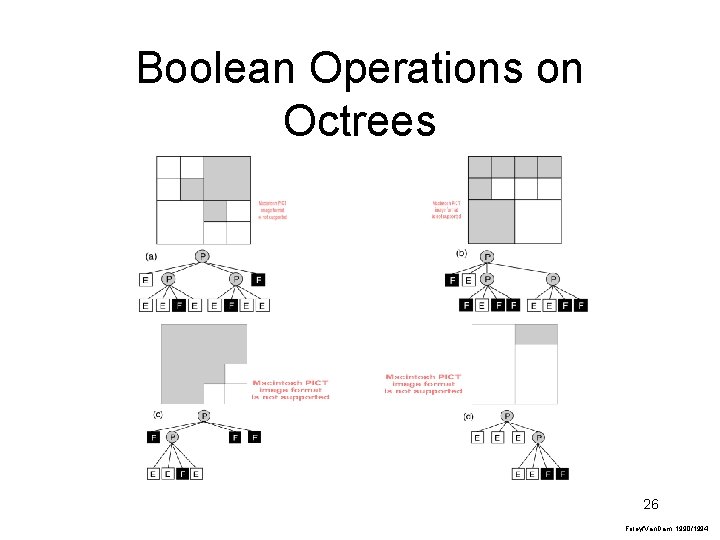
Boolean Operations on Octrees 26 Foley/Van. Dam, 1990/1994

Applications for Spatial Occupancy Enumeration • Many different applications – – – GIS Medical Engineering Simulation Volume Rendering Video Gaming Approximating real-world data – …. 27

Issues with Spatial Occupancy Enumeration • Approximate – Kind of like faceting a surface, discretizing 3 D space – Operationally, the combinatorics (as opposed to the numerics) can be challenging – Not as good for applications wanting exact computation (e. g. tool path programming) 28

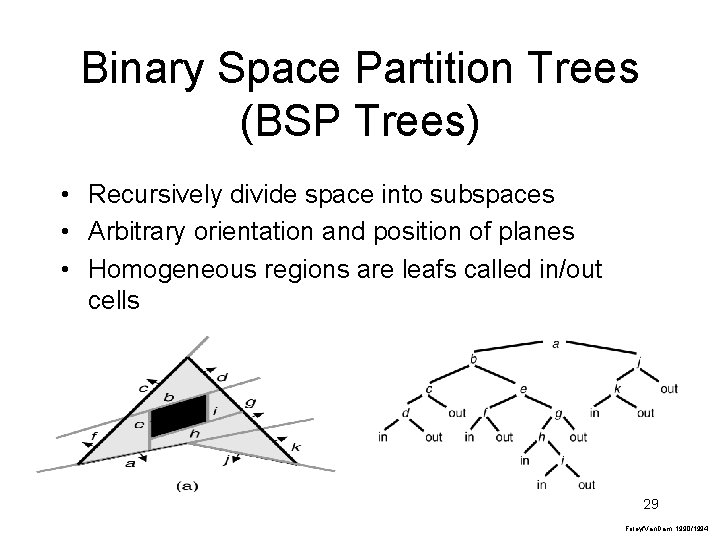
Binary Space Partition Trees (BSP Trees) • Recursively divide space into subspaces • Arbitrary orientation and position of planes • Homogeneous regions are leafs called in/out cells 29 Foley/Van. Dam, 1990/1994

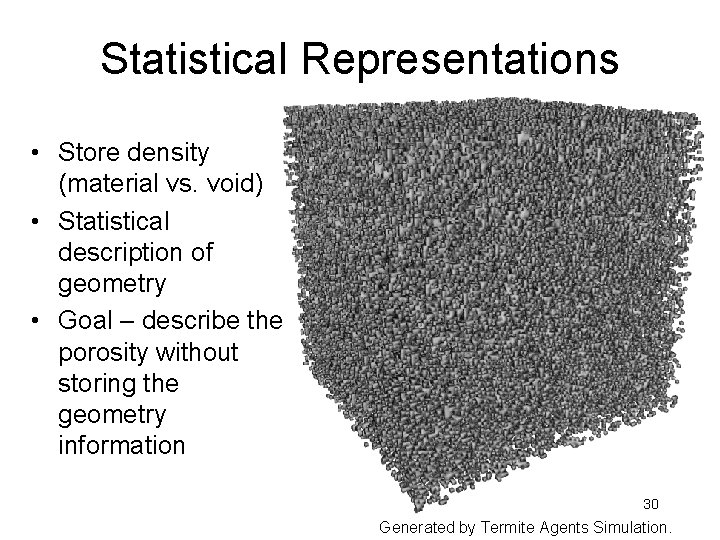
Statistical Representations • Store density (material vs. void) • Statistical description of geometry • Goal – describe the porosity without storing the geometry information 30 Generated by Termite Agents Simulation.

Stochastic Functions • Need some way of converting a solid into some representative statistical form • From each material voxel, calculate the distance to the nearest voxel that is not material • Repeat for void voxels • Store distributions: – one for empty space – one for material – density value 31 Distance vs. Probability

Application • • Bone tissue MRI data Other biological data Solid modeling MRI scan of left shoulder Bone matrix from scanned data 32

End 33