CS 4300 Computer Graphics Prof Harriet Fell CS

CS 4300 Computer Graphics Prof. Harriet Fell CS 4300 Lectures 13, 14 – October 5, 6, 2011 May 22, 2021 College of Computer and Information Science, Northeastern University 1

Today’s Topics • • • Curves Fitting Curves to Data Points Splines Hermite Cubics Bezier Cubics May 22, 2021 College of Computer and Information Science, Northeastern University 2

Curves A curve is the continuous image of an interval in n-space. Implicit f(x, y) = 0 x 2 + y 2 – R 2 = 0 B Parametric (x(t), y(t)) = P(t) A Generative proc (x, y) May 22, 2021 P(t) = t. A + (1 -t)B College of Computer and Information Science, Northeastern University 3

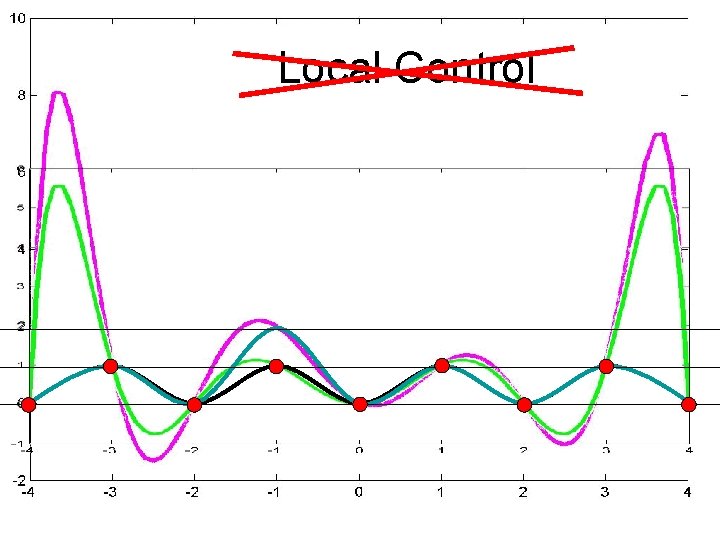
Curve Fitting We want a curve that passes through control points. interpolating curve Or a curve that passes near control points. approximating curve How do we create a good curve? What makes a good curve? May 22, 2021 College of Computer and Information Science, Northeastern University 4

Axis Independence If we rotate the set of control points, we should get the rotated curve. May 22, 2021 College of Computer and Information Science, Northeastern University 5

Local Control

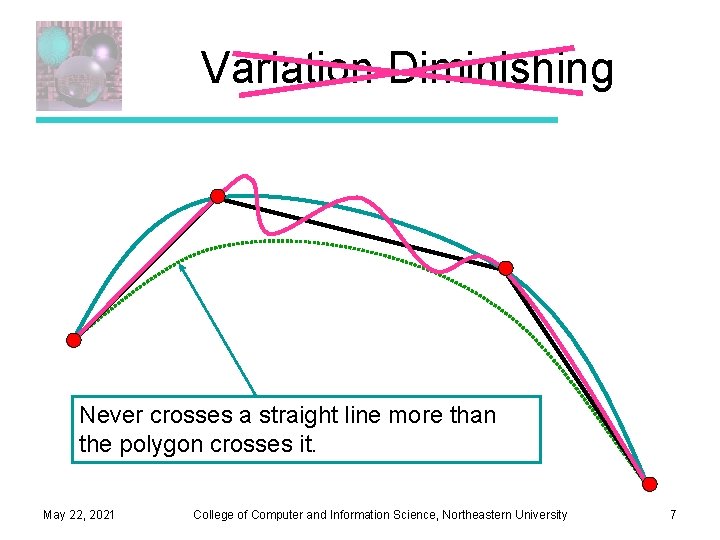
Variation Diminishing Never crosses a straight line more than the polygon crosses it. May 22, 2021 College of Computer and Information Science, Northeastern University 7

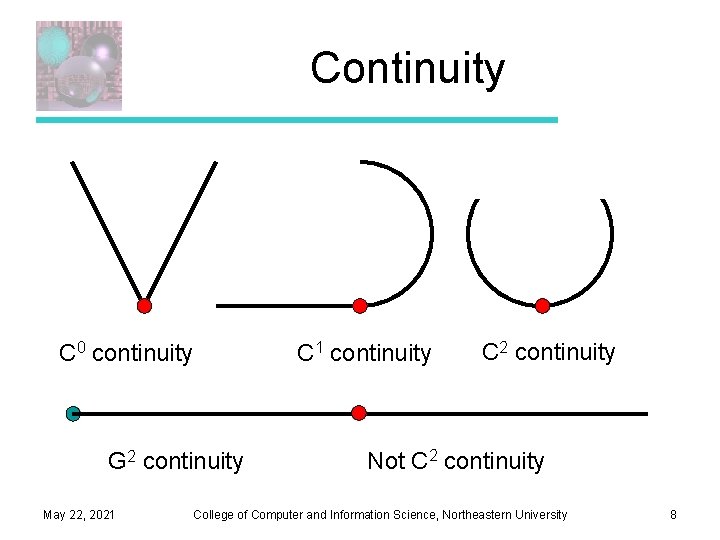
Continuity C 0 continuity G 2 continuity May 22, 2021 C 1 continuity C 2 continuity Not C 2 continuity College of Computer and Information Science, Northeastern University 8

How do we Fit Curves? The Lagrange interpolating polynomial is the polynomial of degree n-1 that passes through the n points, (x 1, y 1), (x 2, y 2), …, (xn, yn), and is given by Lagrange Interpolating Polynomial from mathworld May 22, 2021 College of Computer and Information Science, Northeastern University 9

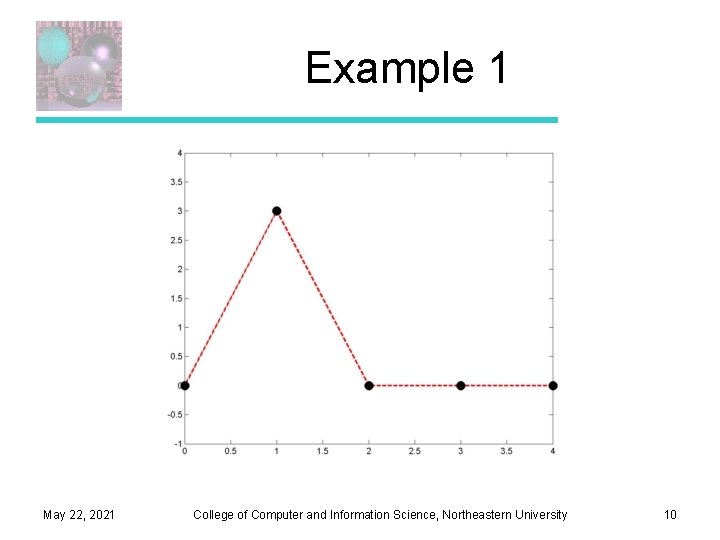
Example 1 May 22, 2021 College of Computer and Information Science, Northeastern University 10

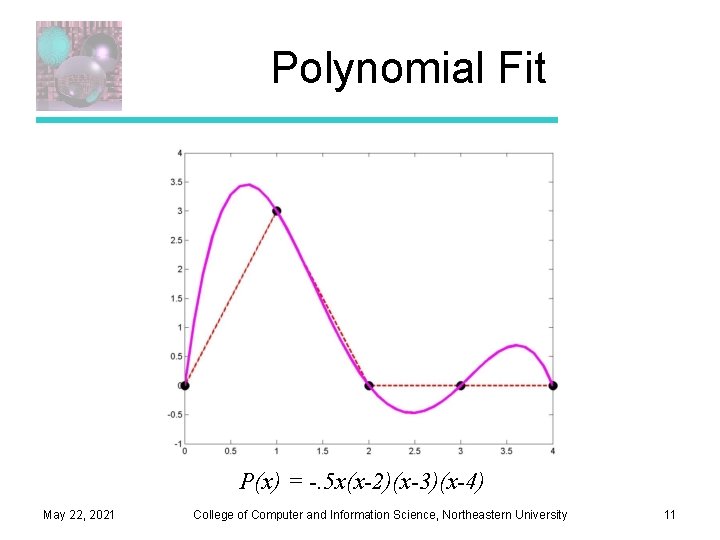
Polynomial Fit P(x) = -. 5 x(x-2)(x-3)(x-4) May 22, 2021 College of Computer and Information Science, Northeastern University 11

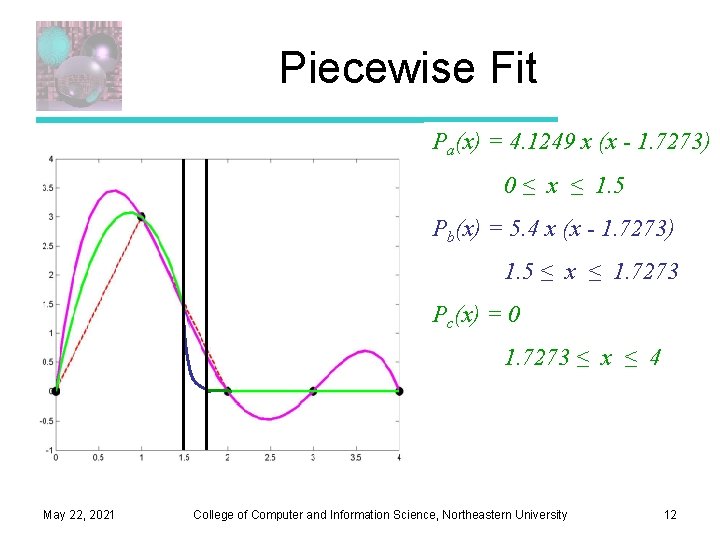
Piecewise Fit Pa(x) = 4. 1249 x (x - 1. 7273) 0 ≤ x ≤ 1. 5 Pb(x) = 5. 4 x (x - 1. 7273) 1. 5 ≤ x ≤ 1. 7273 Pc(x) = 0 1. 7273 ≤ x ≤ 4 May 22, 2021 College of Computer and Information Science, Northeastern University 12

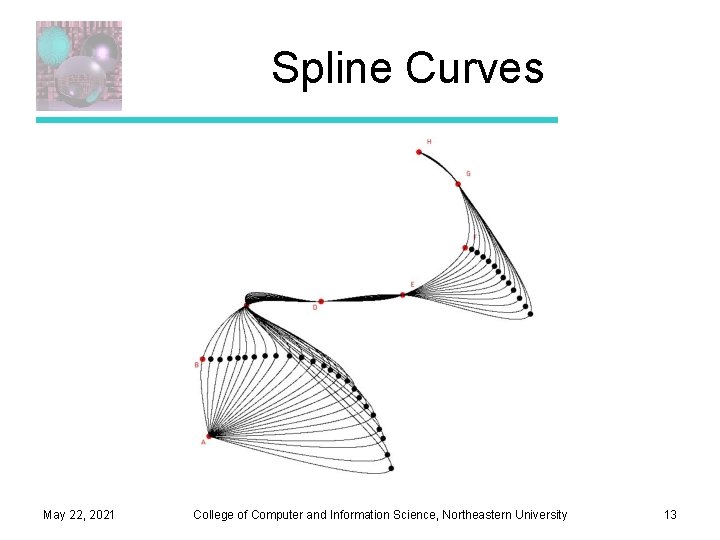
Spline Curves May 22, 2021 College of Computer and Information Science, Northeastern University 13

Splines and Spline Ducks Marine Drafting Weights http: //www. frets. com/FRETSPages/Luthier/Tips. Tricks/Drafting. Weights/draftweights. html May 22, 2021 College of Computer and Information Science, Northeastern University 14

Drawing Spline Today (esc) 1. Draw some curves in Power. Point. 2. Look at Perlin’s B-Spline Applet. May 22, 2021 College of Computer and Information Science, Northeastern University 15

May 22, 2021 College of Computer and Information Science, Northeastern University 16

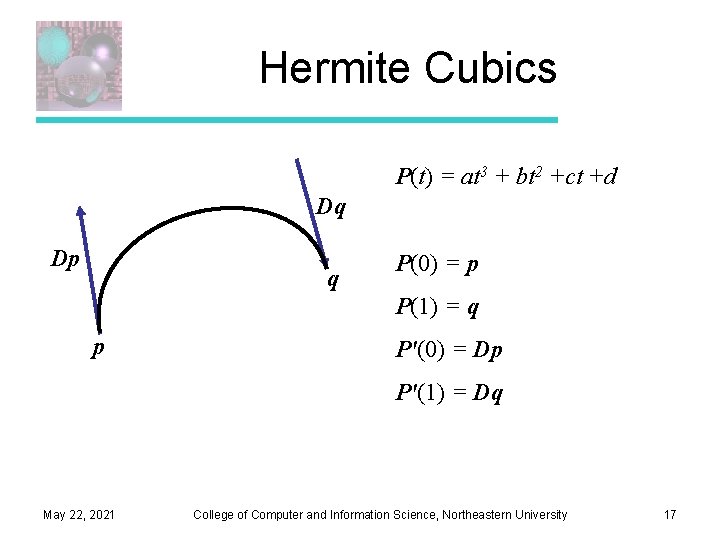
Hermite Cubics P(t) = at 3 + bt 2 +ct +d Dq Dp q P(0) = p P(1) = q p P'(0) = Dp P'(1) = Dq May 22, 2021 College of Computer and Information Science, Northeastern University 17

Hermite Coefficients P(t) = at 3 + bt 2 +ct +d P(0) = p P(1) = q P'(0) = Dp P'(1) = Dq For each coordinate, we have 4 linear equations in 4 unknowns May 22, 2021 College of Computer and Information Science, Northeastern University 18

Boundary Constraint Matrix May 22, 2021 College of Computer and Information Science, Northeastern University 19

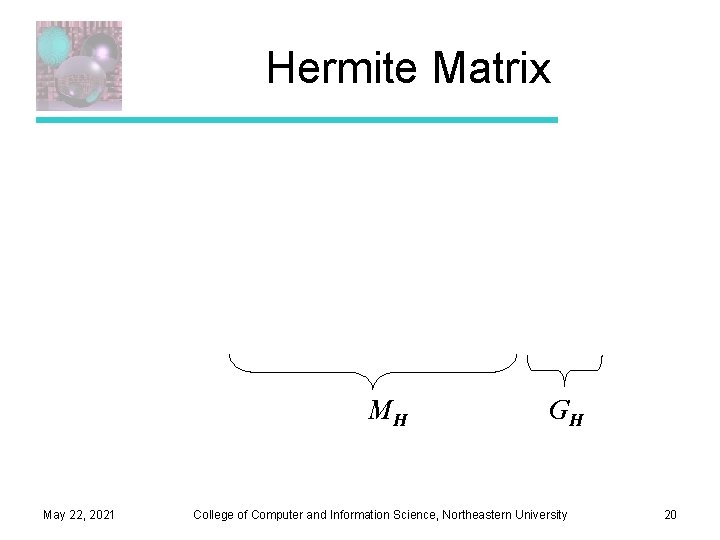
Hermite Matrix MH May 22, 2021 GH College of Computer and Information Science, Northeastern University 20

Hermite Blending Functions May 22, 2021 College of Computer and Information Science, Northeastern University 21

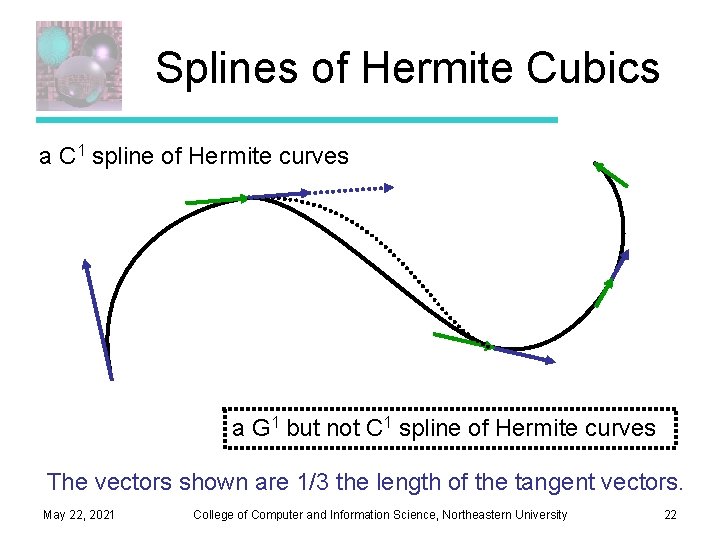
Splines of Hermite Cubics a C 1 spline of Hermite curves a G 1 but not C 1 spline of Hermite curves The vectors shown are 1/3 the length of the tangent vectors. May 22, 2021 College of Computer and Information Science, Northeastern University 22

Computing the Tangent Vectors Catmull-Rom Spline p 3 p 5 p 2 p 4 P(0) = p 3 p 1 P(1) = p 4 P'(0) = ½(p 4 - p 2 ) P'(1) = ½(p 5 - p 3 ) May 22, 2021 College of Computer and Information Science, Northeastern University 23

Cardinal Spline The Catmull-Rom spline P(0) = p 3 is a special case of the Cardinal spline P(1) = p 4 P(0) = p 3 P'(0) = ½(p 4 - p 2 ) P(1) = p 4 P'(1) = ½(p 5 - p 3 ) P'(0) = (1 - t)(p 4 - p 2 ) P'(1) = (1 - t)(p 5 - p 3 ) 0 ≤ t ≤ 1 is the tension. May 22, 2021 College of Computer and Information Science, Northeastern University 24

Drawing Hermite Cubics • How many points should we draw? • Will the points be evenly distributed if we use a constant increment on t ? • We actually draw Bezier cubics. May 22, 2021 College of Computer and Information Science, Northeastern University 25

General Bezier Curves May 22, 2021 College of Computer and Information Science, Northeastern University 26

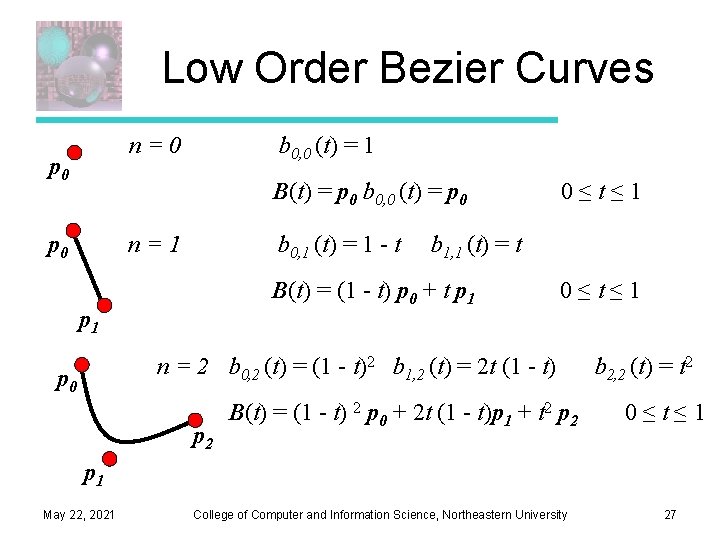
Low Order Bezier Curves n=0 p 0 b 0, 0 (t) = 1 B(t) = p 0 b 0, 0 (t) = p 0 n=1 p 0 b 0, 1 (t) = 1 - t b 1, 1 (t) = t B(t) = (1 - t) p 0 + t p 1 0≤t≤ 1 n = 2 b 0, 2 (t) = (1 - t)2 b 1, 2 (t) = 2 t (1 - t) p 0 p 2 B(t) = (1 - t) 2 p 0 + 2 t (1 - t)p 1 + t 2 p 2 b 2, 2 (t) = t 2 0≤t≤ 1 p 1 May 22, 2021 College of Computer and Information Science, Northeastern University 27

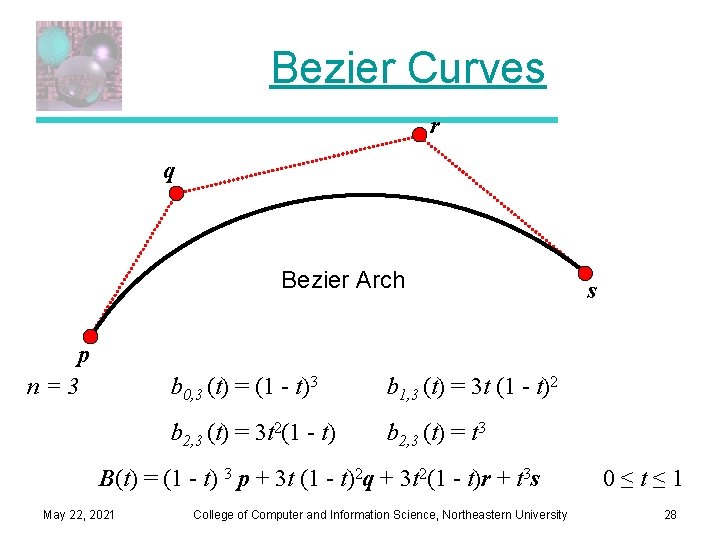
Bezier Curves r q Bezier Arch p n=3 b 0, 3 (t) = (1 - t)3 b 1, 3 (t) = 3 t (1 - t)2 b 2, 3 (t) = 3 t 2(1 - t) b 2, 3 (t) = t 3 B(t) = (1 - t) 3 p + 3 t (1 - t)2 q + 3 t 2(1 - t)r + t 3 s May 22, 2021 College of Computer and Information Science, Northeastern University s 0≤t≤ 1 28

Bezier Matrix B(t) = (1 - t) 3 p + 3 t (1 - t)2 q + 3 t 2(1 - t)r + t 3 s B(t) = a t 3 + bt 2 + ct + d 0≤t≤ 1 MB May 22, 2021 0≤t≤ 1 GB College of Computer and Information Science, Northeastern University 29

Geometry Vector May 22, 2021 College of Computer and Information Science, Northeastern University 30

Properties of Bezier Curves May 22, 2021 College of Computer and Information Science, Northeastern University 31

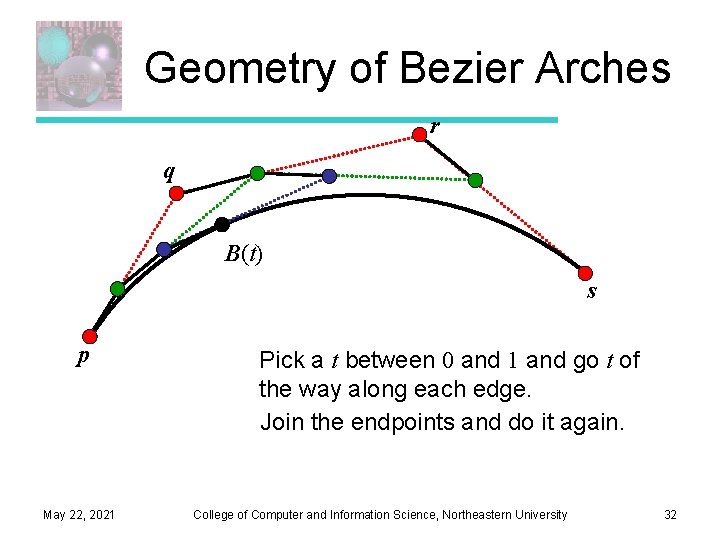
Geometry of Bezier Arches r q B(t) s p May 22, 2021 Pick a t between 0 and 1 and go t of the way along each edge. Join the endpoints and do it again. College of Computer and Information Science, Northeastern University 32

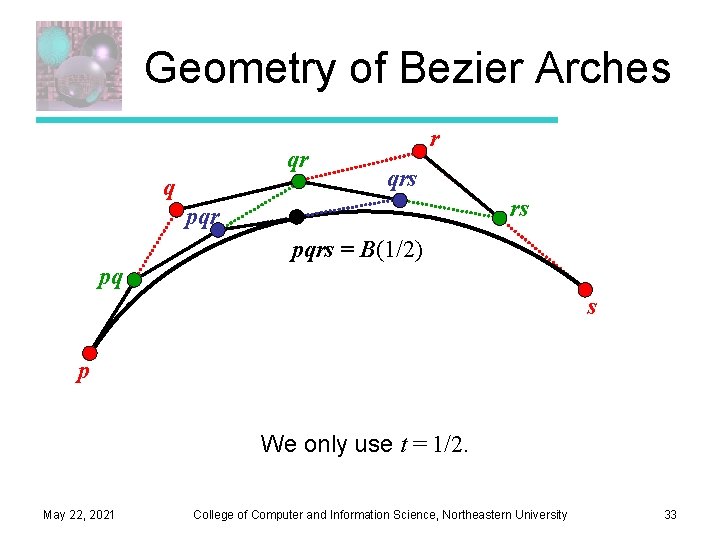
Geometry of Bezier Arches qr q r qrs rs pqrs = B(1/2) pq s p We only use t = 1/2. May 22, 2021 College of Computer and Information Science, Northeastern University 33

draw. Arch(P, Q, R, S){ if (Arch. Size(P, Q, R, S) <=. 5 ) Dot(P); else{ PQ = (P + Q)/2; QR = (Q + R)/2; RS = (R + S)/2; PQR = (PQ + QR)/2; QRS = (QR + RS)/2; PQRS = (PQR + QRS)/2 draw. Arch(P, PQR, PQRS); draw. Arch(PQRS, RS, S); } }

Putting it All Together • Bezier Arches and Catmull-Rom Splines May 22, 2021 College of Computer and Information Science, Northeastern University 35