CS 430 Computer Graphics CohenSutherland Line Clipping Algorithm

CS 430 Computer Graphics Cohen-Sutherland Line Clipping Algorithm Chi-Cheng Lin, Winona State University

Topics Clipping l Cohen-Sutherland Line Clipping Algorithm l 2

Clipping l Why clipping? z. Not everything defined in the world coordinates is inside the world window l Where does clipping take place? Model l Clipping Viewport Transformation … Open. GL does it for you z. BUT, as a CS major, you should know how it is done. 3

Line Clipping l int clip. Segment(p 1, p 2, window) z. Input parameters: p 1, p 2, window p 1, p 2: 2 D endpoints that define a line window: aligned rectangle z. Returned value: 1, if part of the line is inside the window 0, otherwise z. Output parameters: p 1, p 2 p 1 and/or p 2’s value might be changed so that both p 1 and p 2 are inside the window 4

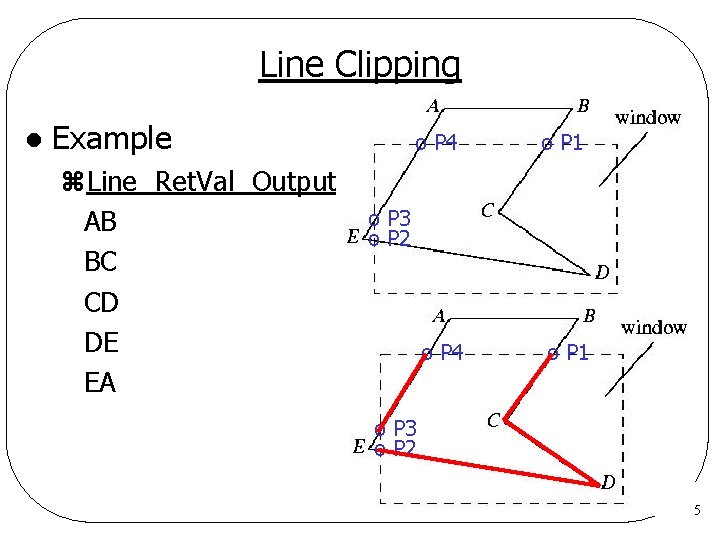
Line Clipping l Example z. Line Ret. Val Output AB BC CD DE EA o P 4 o P 1 o P 3 o P 2 5

Cohen-Sutherland Line Clipping Algorithm l Trivial accept and trivial reject z. If both endpoints within window trivial accept z. If both endpoints outside of same boundary of window trivial reject l Otherwise z. Clip against each edge in turn Throw away “clipped off” part of line each time l How can we do it efficiently (elegantly)? 6

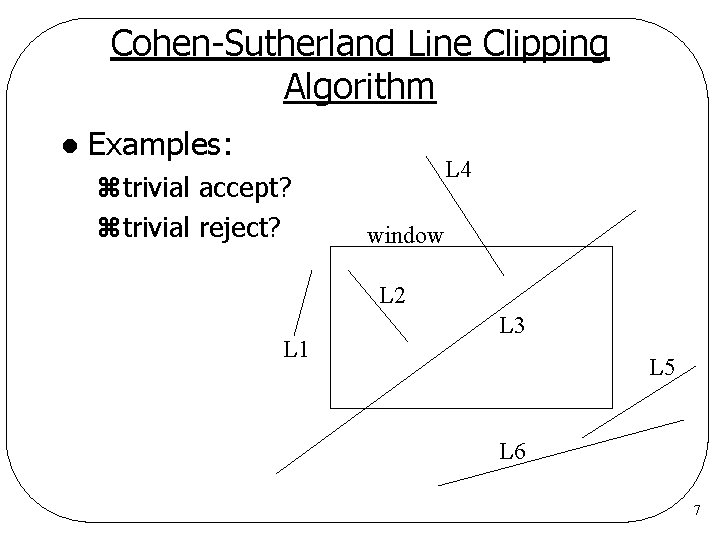
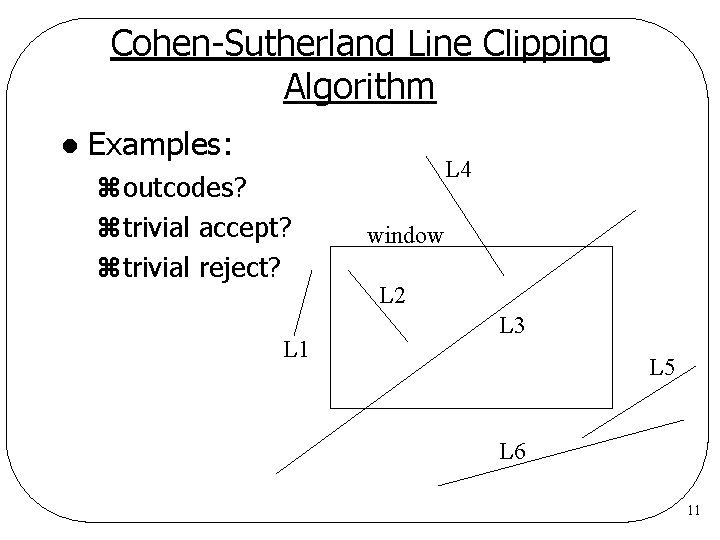
Cohen-Sutherland Line Clipping Algorithm l Examples: ztrivial accept? ztrivial reject? L 4 window L 2 L 1 L 3 L 5 L 6 7

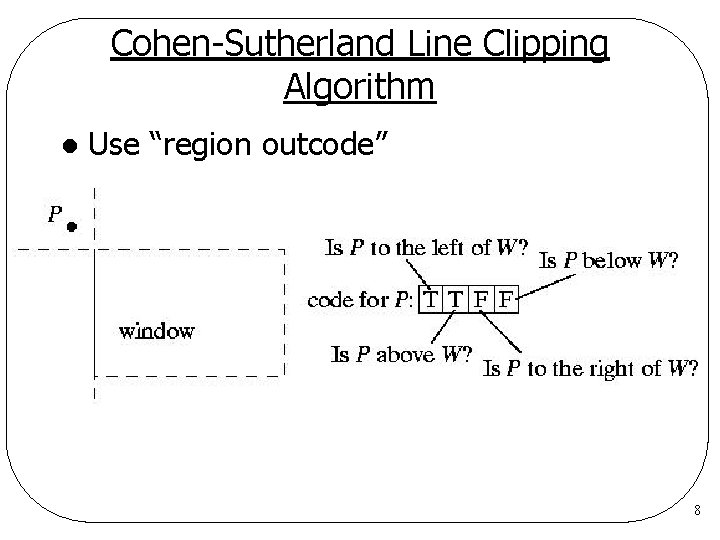
Cohen-Sutherland Line Clipping Algorithm l Use “region outcode” 8

Cohen-Sutherland Line Clipping Algorithm l outcode[1] outcode[2] outcode[3] outcode[4] (x (y < > > < Window. left) Window. top) Window. right) Window. bottom) 9

Cohen-Sutherland Line Clipping Algorithm l Both outcodes are FFFF z. Trivial accept l Logical AND of two outcodes FFFF z. Trivial reject l Logical AND of two outcodes = FFFF z. Can’t tell z. Clip against each edge in turn Throw away “clipped off” part of line each time 10

Cohen-Sutherland Line Clipping Algorithm l Examples: zoutcodes? ztrivial accept? ztrivial reject? L 1 L 4 window L 2 L 3 L 5 L 6 11

Cohen-Sutherland Line Clipping Algorithm int clip. Segment(Point 2& p 1, Point 2& p 2, Real. Rect W) do if(trivial accept) return 1; else if(trivial reject) return 0; else if(p 1 is inside) swap(p 1, p 2) if(p 1 is to the left) chop against the left else if(p 1 is to the right) chop against the right else if(p 1 is below) chop against the bottom else if(p 1 is above) chop against the top while(1); 12

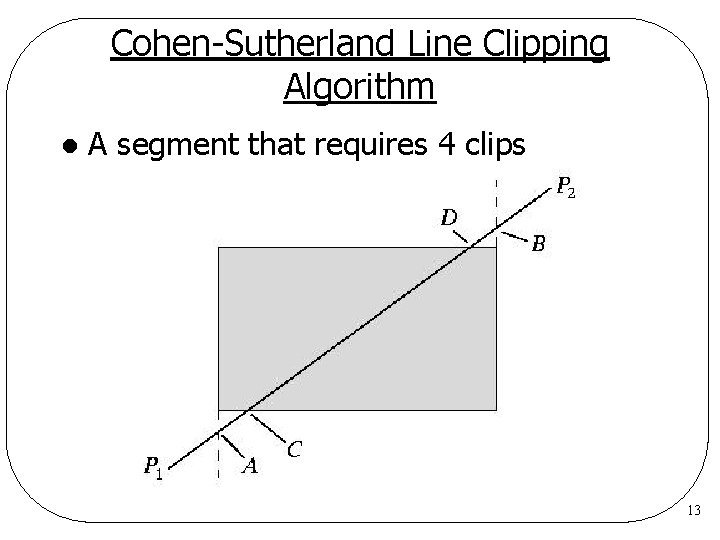
Cohen-Sutherland Line Clipping Algorithm l A segment that requires 4 clips 13

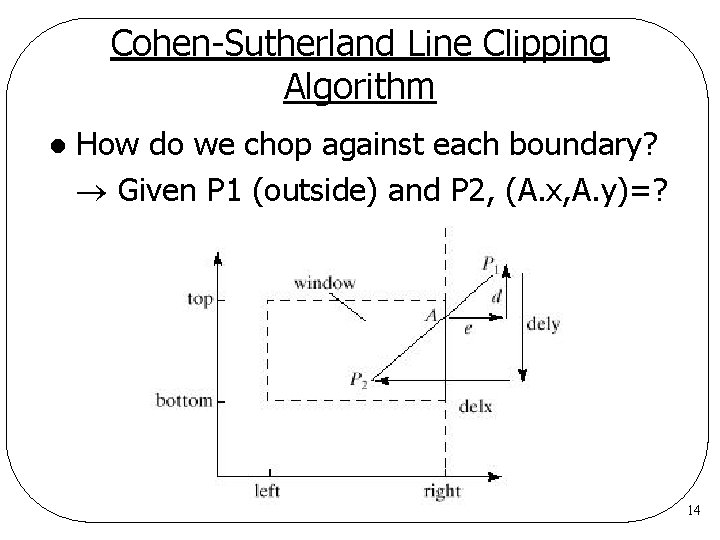
Cohen-Sutherland Line Clipping Algorithm l How do we chop against each boundary? Given P 1 (outside) and P 2, (A. x, A. y)=? 14

Cohen-Sutherland Line Clipping Algorithm l Let dx = p 1. x - p 2. x dy = p 1. y - p 2. y A. x = w. r d = p 1. y - A. y e = p 1. x - w. r d/dy = e/dx p 1. y - A. y = (dy/dx)(p 1. x - w. r) A. y = p 1. y - (dy/dx)(p 1. x - w. r) = p 1. y + (dy/dx)(w. r - p 1. x) As A is the new P 1 p 1. y += (dy/dx)(w. r - p 1. x) p 1. x = w. r Q: Will we have divided-by-zero problem? 15