CS 412 Introduction to Computer Networking Telecommunication Error

CS 412 Introduction to Computer Networking & Telecommunication Error Correction/Detection Chi-Cheng Lin, Winona State University

Topics l Introduction l Error Correction l Error Detection 2

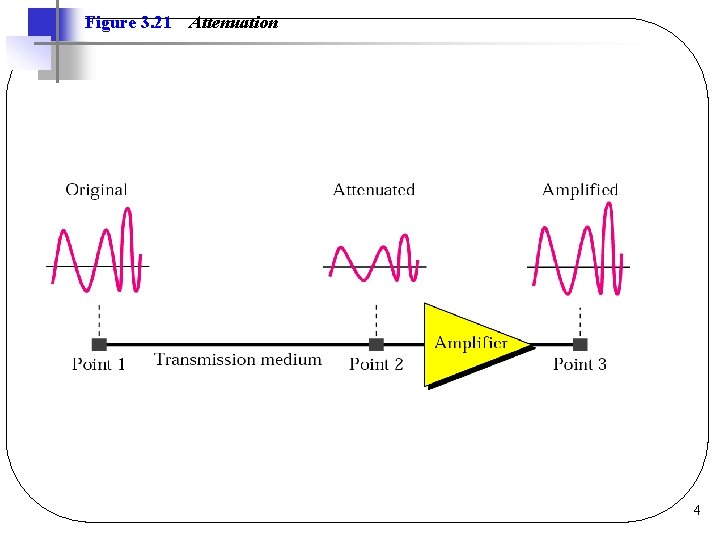
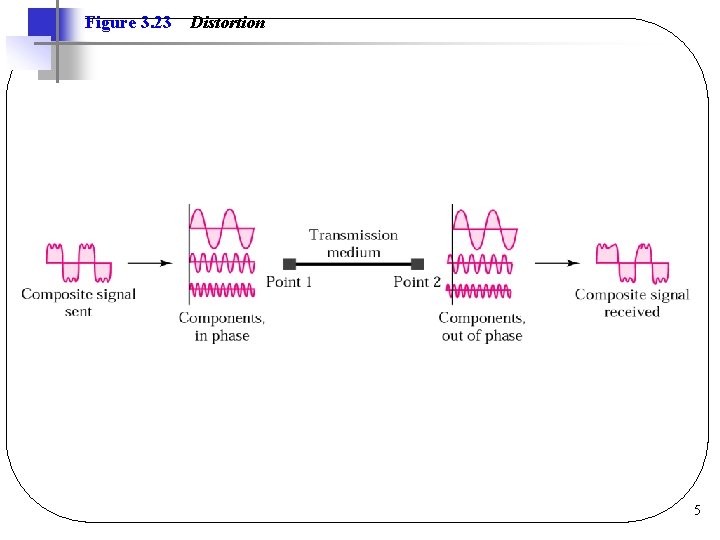
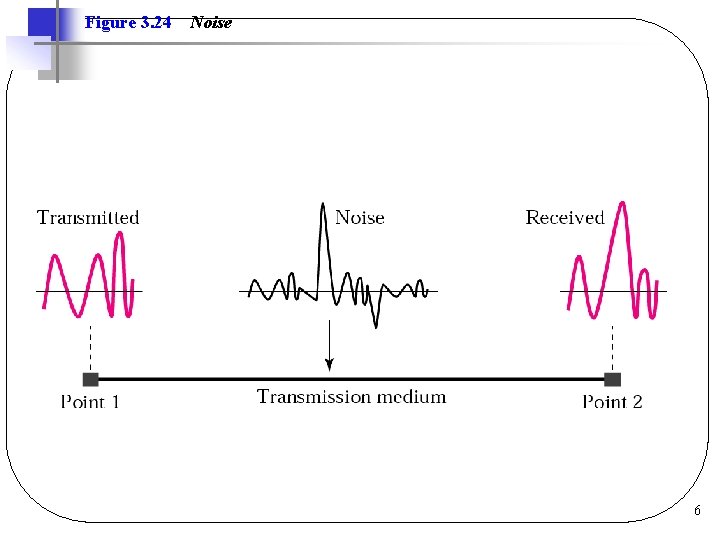
Introduction l Transmission impairments (errors) q. Attenuation ØLoss of energy as signal propagates q. Delay Distortion ØComponents travel at different speeds q. Noise ØUnwanted energy from other sources 3

Figure 3. 21 Attenuation 4

Figure 3. 23 Distortion 5

Figure 3. 24 Noise 6

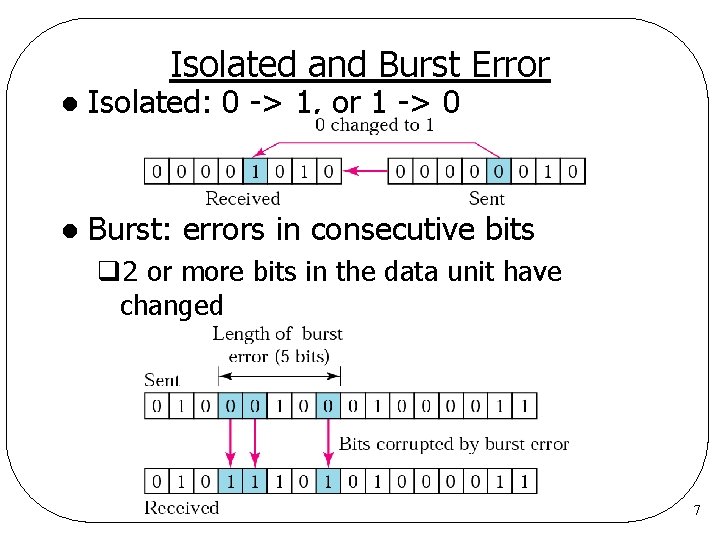
Isolated and Burst Error l Isolated: 0 -> 1, or 1 -> 0 l Burst: errors in consecutive bits q 2 or more bits in the data unit have changed 7

Isolated and Burst Error l Compare burst errors to isolated errors q. Fewer error blocks given a fixed error rate ØExample: error rate: 0. 001 per bit (1 error out of 1000 bits) block size: 1000 bits burst size: 100 isolated error: an error contained in most blocks burst error: 1 or 2 error blocks out of 100 blocks q. Error correction/detection much harder 8

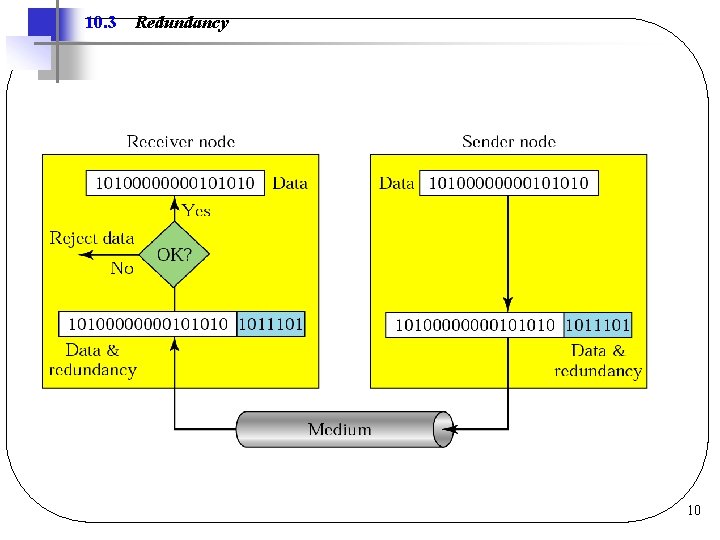
Error Correcting/Detecting Codes Redundancy added to data l Error correction l q. Referred to as forward error correction q. Detect and correct error l Error detection q. Detect error and request retransmission l Codeword (n bits) qdata + redundancy (m bits) (r bits) qn = m + r When to use which one? 9

10. 3 Redundancy 10

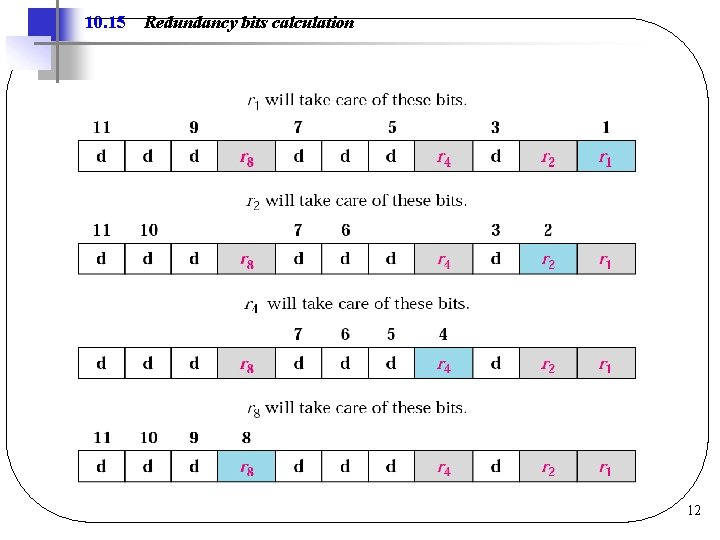
Error Correction l Hamming Code q. For m-bit data we need r-bit redundancy, where (m+r+1) 2 r q. Redundancy bits are placed in position of 2’s power l Example: If m = 7, then r = 4 11

10. 15 Redundancy bits calculation 12

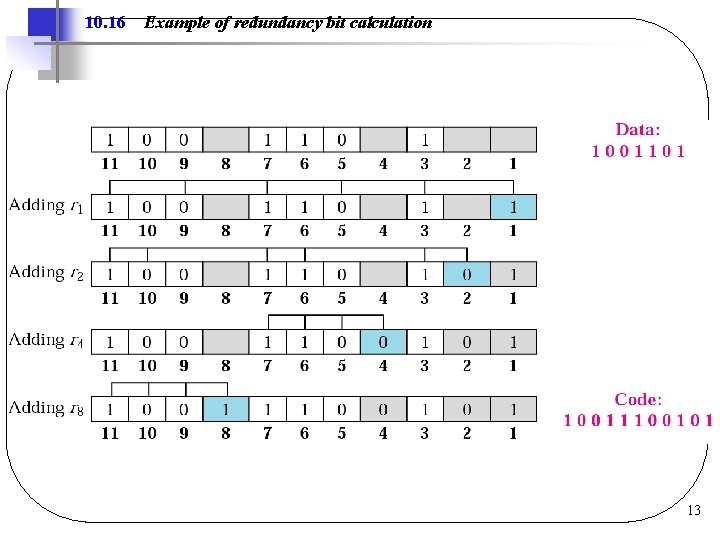
10. 16 Example of redundancy bit calculation 13

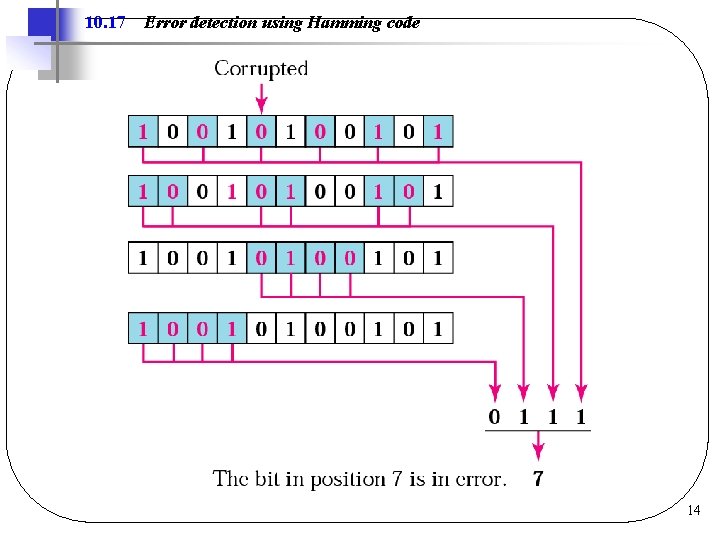
10. 17 Error detection using Hamming code 14

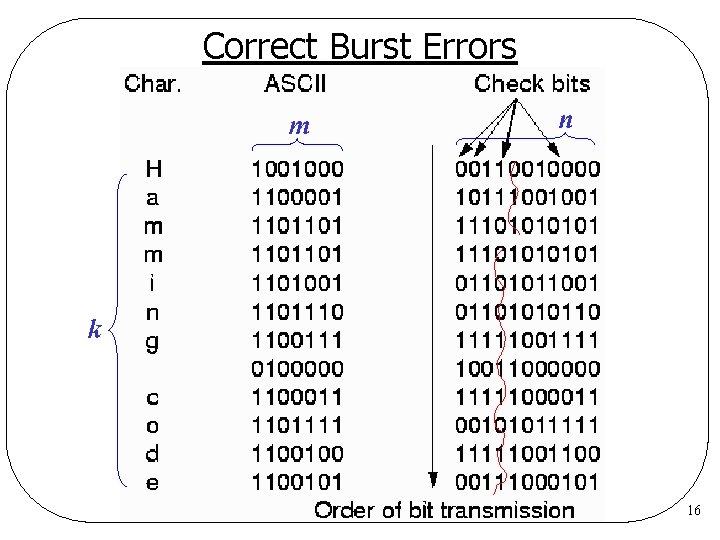
Correct Burst Errors l Organize k codewords into a (k x n) matrix q(k x r) check bits for (k x m) data Transmit one column at a time l Reconstruct matrix after received l Correct burst errors of length k l 15

Correct Burst Errors m n k 16

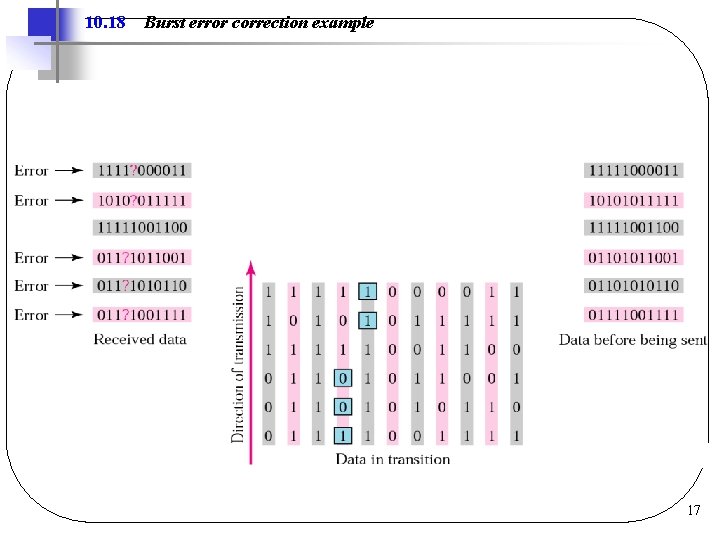
10. 18 Burst error correction example 17

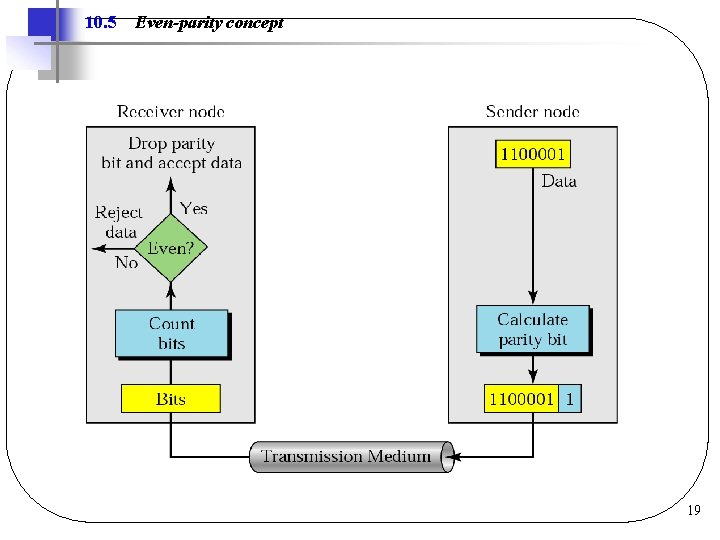
Error Detection l Parity bit q. Error detection q. Added to data so that number of 1 bits in codeword is ØEven (even parity) ØOdd (odd parity) q. E. g. , ASCII of ‘H’ is 1001000, its codeword is Ø 01001000 ____ if even parity is used Ø 11001000 ____ if odd parity is used 18

10. 5 Even-parity concept 19

Error Detection vs. Correction l Error-detecting and retransmission q. More efficient than error-correction when error rate is low l Example: qerror rate: 0. 000001 per bit block size: 1000 bits check bits per block: Hamming code error correction: 10 Parity code error detection: 1 overhead for 1 M data: e. c. 10000 bits e. d. 2001 bits 20

Use Parity to Detect Burst Errors Organize a block into (k x n) matrix l One parity for each column one row of parities at the bottom l Transmit one row at a time l Can detect burst errors of length n l 21

Example Original data 11100111 1101 00111001 10101001 Organized into 11100111 1101 00111001 10101010 LRC Transmitted 11100111 1101 00111001 10101010 Burst error 11100111 11010000 01001001 10101010 Error detected whole block is discarded 11100111 110100001 10101010 22

Error-Detecting Code - CRC Bit stream is treated as polynomial w/ coefficients 0 and 1 l Example: l qdata: polynomial: 10100111 degree = 7 l Modulo 2 arithmetic is used q. Example: q. XOR 10011011 11110000 +11001010 -10100110 01010001 01010110 23

Error-Detecting Code - CRC l Use generator polynomial G(x) to calculate checksum q. Frame: P(x) generator: G(x) degree of G(x) = d Transmitted: checksummed frame P(x)·xd + R(x) l It’s guaranteed that P(x)·xd + R(x) is divisible by G(x)!! 24

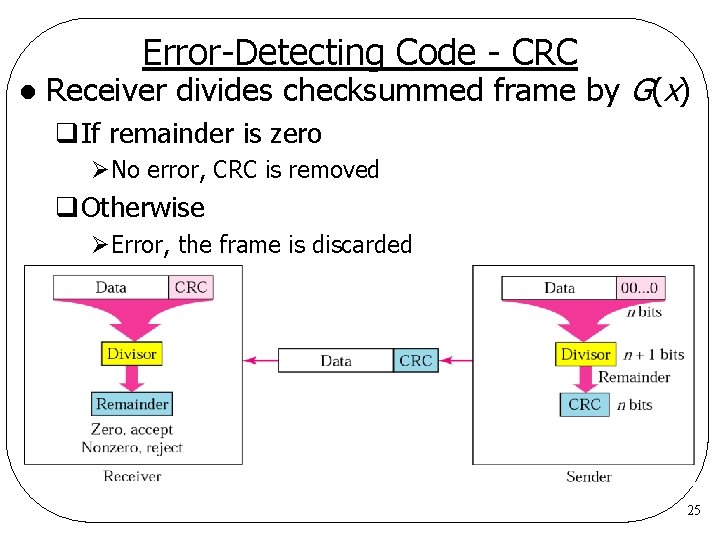
Error-Detecting Code - CRC l Receiver divides checksummed frame by G(x) q. If remainder is zero ØNo error, CRC is removed q. Otherwise ØError, the frame is discarded 25

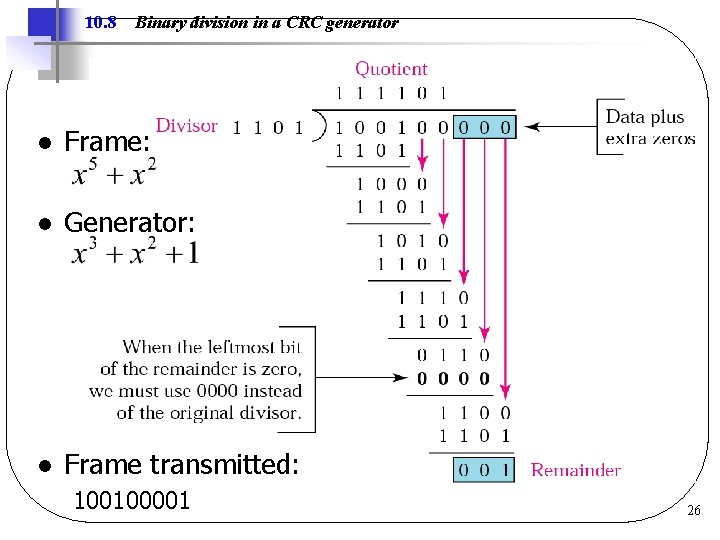
10. 8 Binary division in a CRC generator l Frame: l Generator: l Frame transmitted: 100100001 26

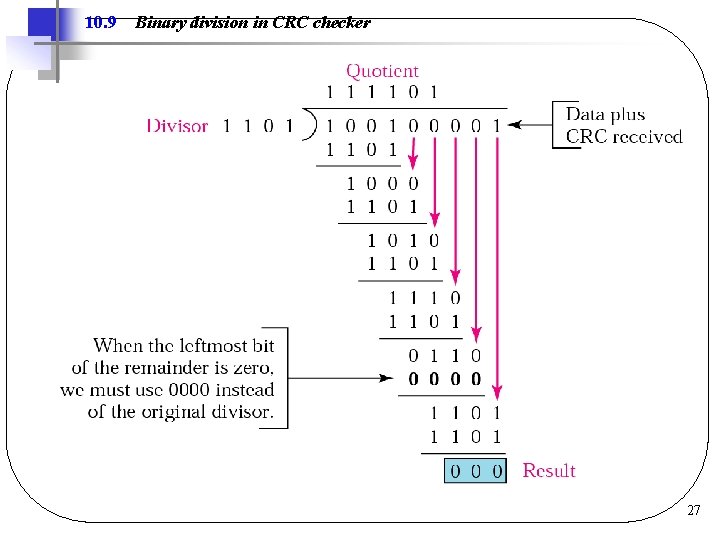
10. 9 Binary division in CRC checker 27

CRC - Example l Frame: l Generator: 110000 28

CRC Properties Single error detection l Double error detection w/ carefully chosen G(x) l Odd number error detection if (x + 1) is a factor of G(x) l Detect burst error length r for r check bits l Can be implemented in hardware using simple shift register circuit l 29

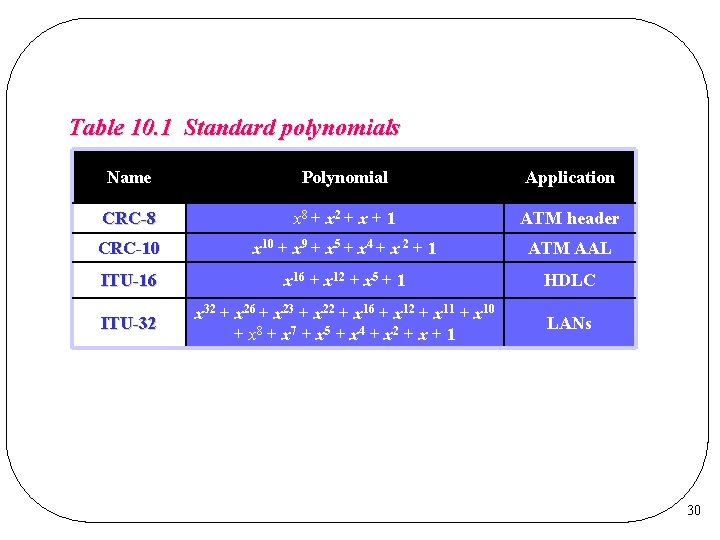
Table 10. 1 Standard polynomials Name Polynomial Application CRC-8 x 8 + x 2 + x + 1 ATM header CRC-10 x 10 + x 9 + x 5 + x 4 + x 2 + 1 ATM AAL ITU-16 x 16 + x 12 + x 5 + 1 HDLC ITU-32 x 32 + x 26 + x 23 + x 22 + x 16 + x 12 + x 11 + x 10 + x 8 + x 7 + x 5 + x 4 + x 2 + x + 1 LANs 30