CS 4102 Algorithms Fall 2020 1 Temp Agency

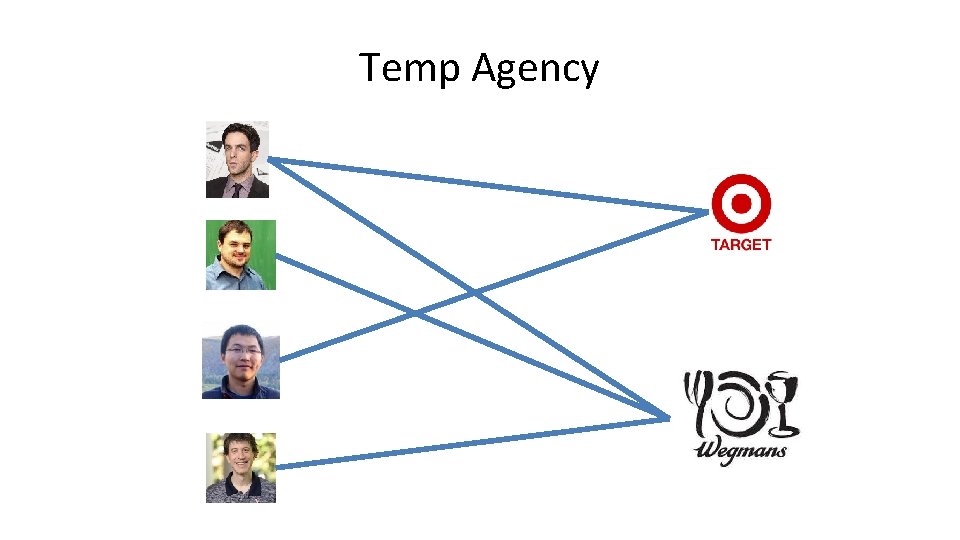











- Slides: 31

CS 4102 Algorithms Fall 2020 1

Temp Agency

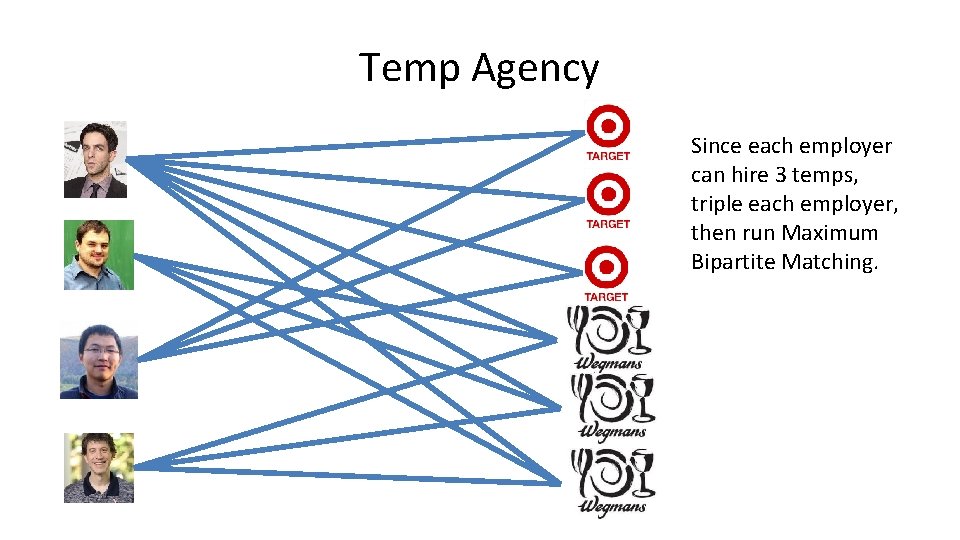
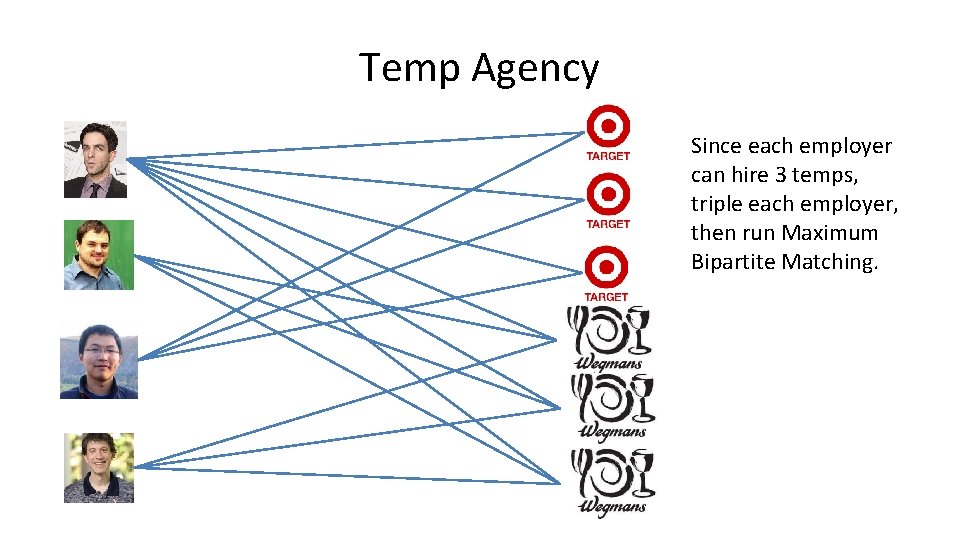
Temp Agency Since each employer can hire 3 temps, triple each employer, then run Maximum Bipartite Matching.

Temp Agency Since each employer can hire 3 temps, triple each employer, then run Maximum Bipartite Matching.

Divide and Conquer* • Divide: – Break the problem into multiple subproblems, each smaller instances of the original • Conquer: – If the suproblems are “large”: • Solve each subproblem recursively – If the subproblems are “small”: • Solve them directly (base case) • Combine: – Merge together solutions to subproblems *CLRS Chapter 4

Dynamic Programming • Requires Optimal Substructure – Solution to larger problem contains the solutions to smaller ones • Idea: 1. Identify recursive structure of the problem 2. Select a good order for solving subproblems • Usually smallest problem first 6

Greedy Algorithms • Require Optimal Substructure – Solution to larger problem contains the solution to a smaller one – Only one subproblem to consider! • Idea: 1. Identify a greedy choice property • How to make a choice guaranteed to be included in some optimal solution 2. Repeatedly apply the choice property until no subproblems remain 7

So far • Divide and Conquer, Dynamic Programming, Greedy – Take an instance of Problem A, relate it to smaller instances of Problem A • Next: – Take an instance of Problem A, relate it to an instance of Problem B 8

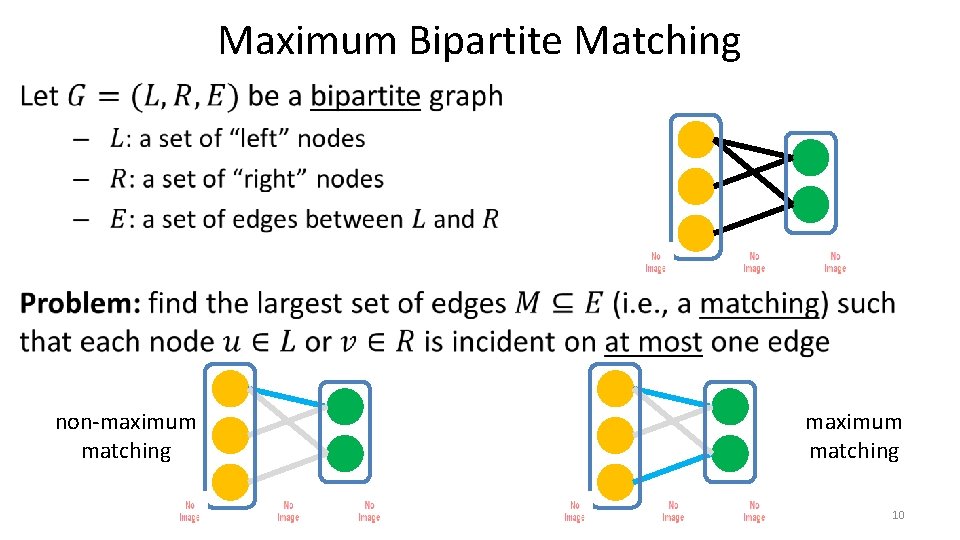
Maximum Bipartite Matching Dog Lovers Dogs 9

Maximum Bipartite Matching • non-maximum matching 10

Maximum Bipartite Matching Using Max Flow 1 1 1 1 11

Reductions • Algorithm technique of supreme ultimate power • Convert instance of problem A to an instance of Problem B • Convert solution of problem B back to a solution of problem A 12

Reductions Shows how two different problems relate to each other ! E M I T E I V MO 13

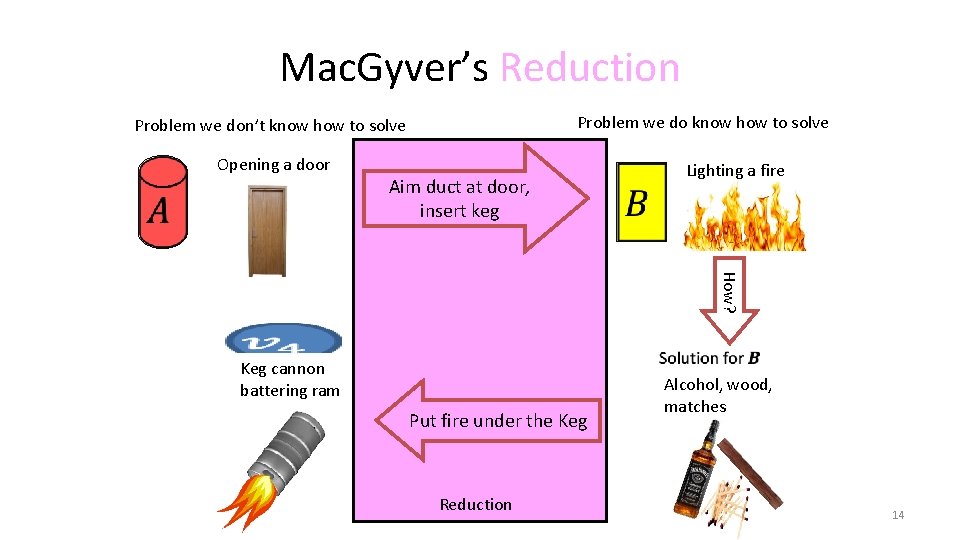
Mac. Gyver’s Reduction Problem we do know how to solve Problem we don’t know how to solve Opening a door Aim duct at door, insert keg Lighting a fire How? Keg cannon battering ram Put fire under the Keg Reduction Alcohol, wood, matches 14

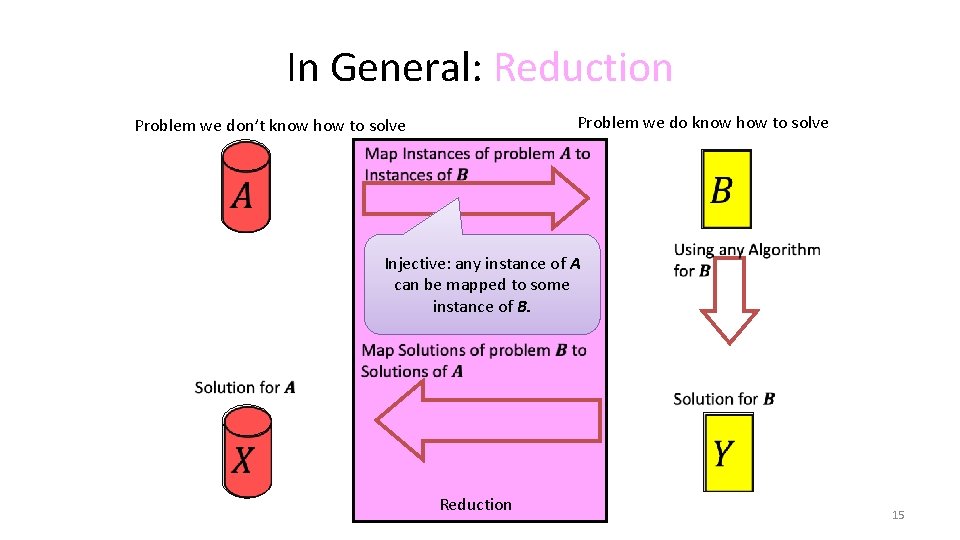
In General: Reduction Problem we do know how to solve Problem we don’t know how to solve Injective: any instance of A can be mapped to some instance of B. Reduction 15

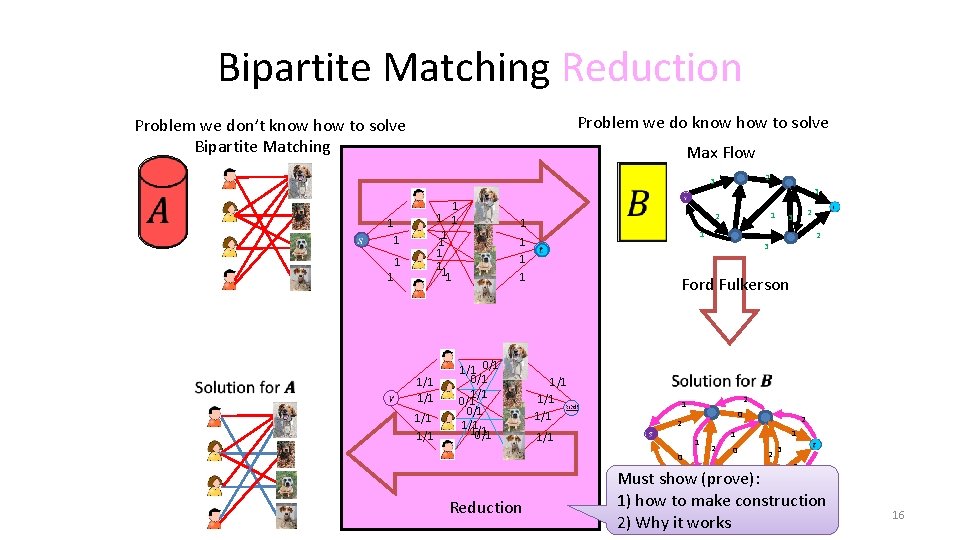
Bipartite Matching Reduction Problem we do know how to solve Problem we don’t know how to solve Bipartite Matching Max Flow 2 3 1 1 1 11 1 1 1/1 1/1 1 2 3 Ford Fulkerson 1/1 1/1 2 1 0 2 1/1 1 0 3 Reduction 3 2 1 1/1 0/1 0/1 1/1 0/1 3 2 1 1 2 0 2 3 1 1 Must show (prove): 2 1) how to make construction 2) Why it works 1 16

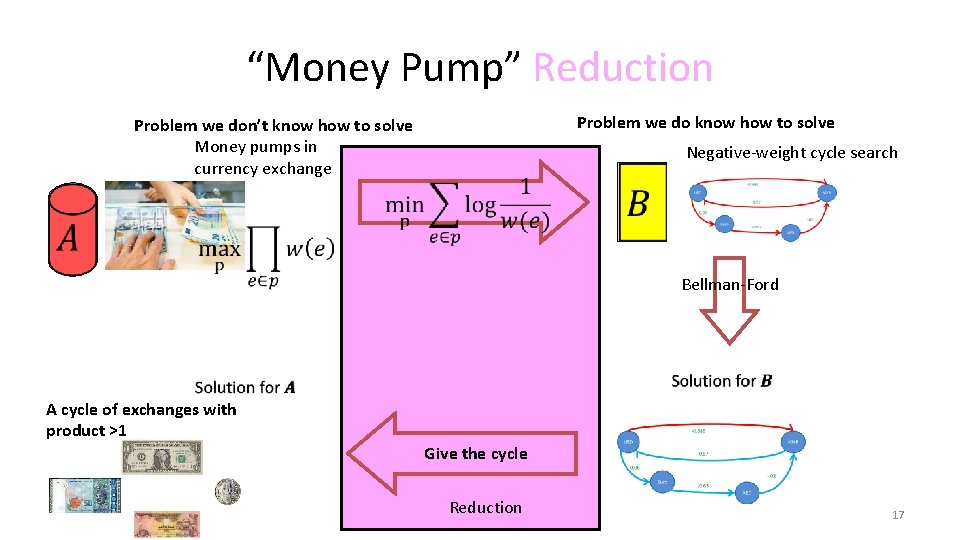
“Money Pump” Reduction Problem we do know how to solve Problem we don’t know how to solve Money pumps in currency exchange Negative-weight cycle search Bellman-Ford A cycle of exchanges with product >1 Give the cycle Reduction 17

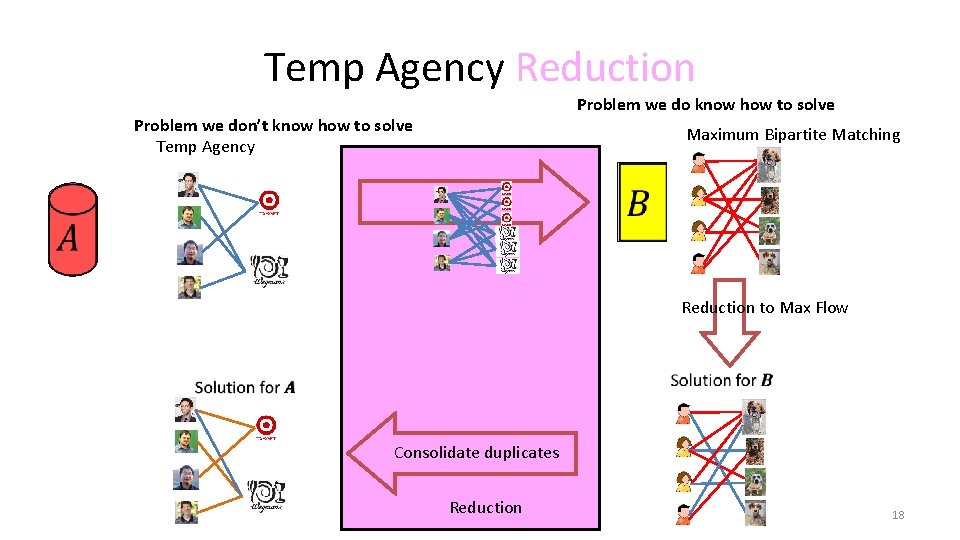
Temp Agency Reduction Problem we do know how to solve Problem we don’t know how to solve Temp Agency Maximum Bipartite Matching Reduction to Max Flow Consolidate duplicates Reduction 18

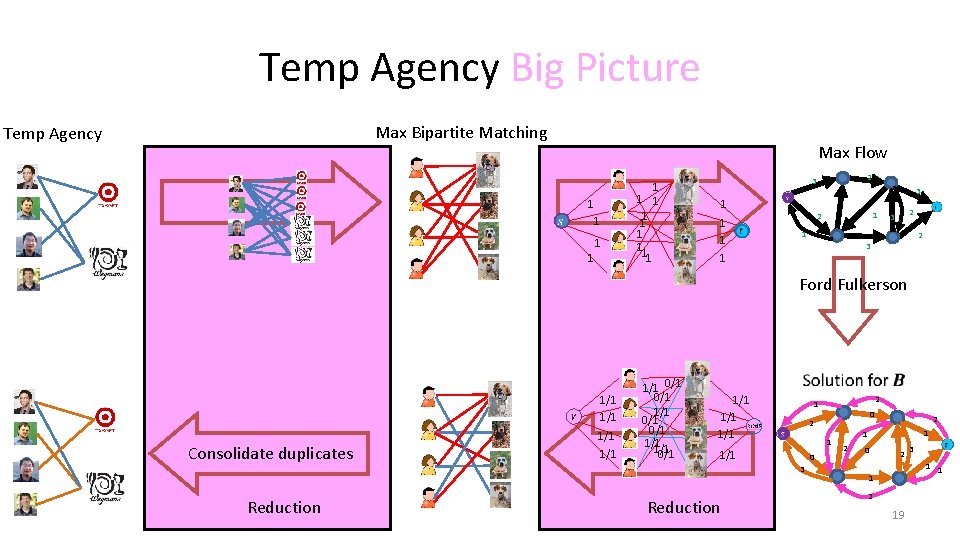
Temp Agency Big Picture Max Bipartite Matching Temp Agency Max Flow 1 1 11 2 3 1 1 3 3 2 1 2 3 Ford Fulkerson 1/1 Consolidate duplicates Reduction 1/1 1/1 0/1 0/1 1/1 1/1 0 2 1 1/1 0 3 Reduction 2 1 1 2 0 2 3 1 1 1 2 19

Reductions for New Algorithms • Create an algorithm for a new problem by using one you already know! • More algorithms = More opportunities! • The problem you reduced to could itself be solved using a reduction!

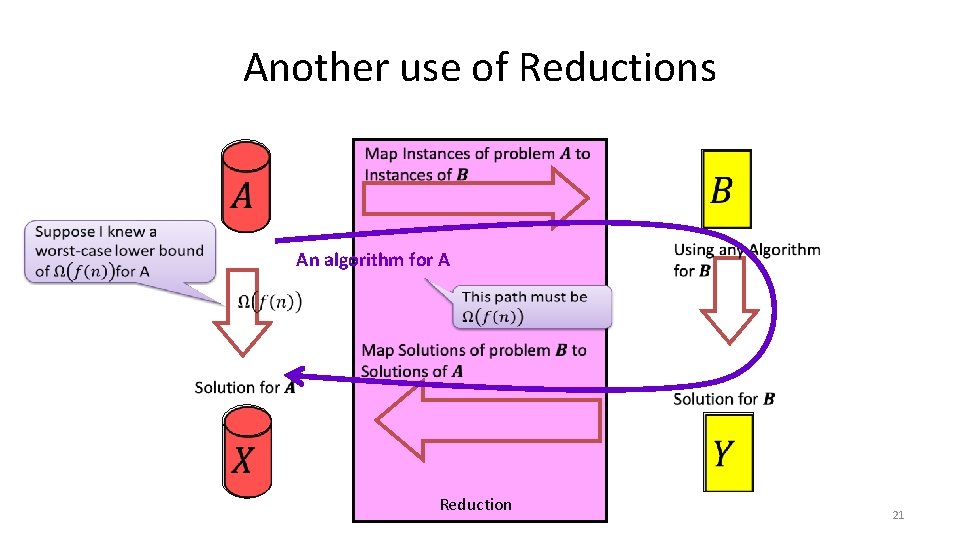
Another use of Reductions An algorithm for A Reduction 21

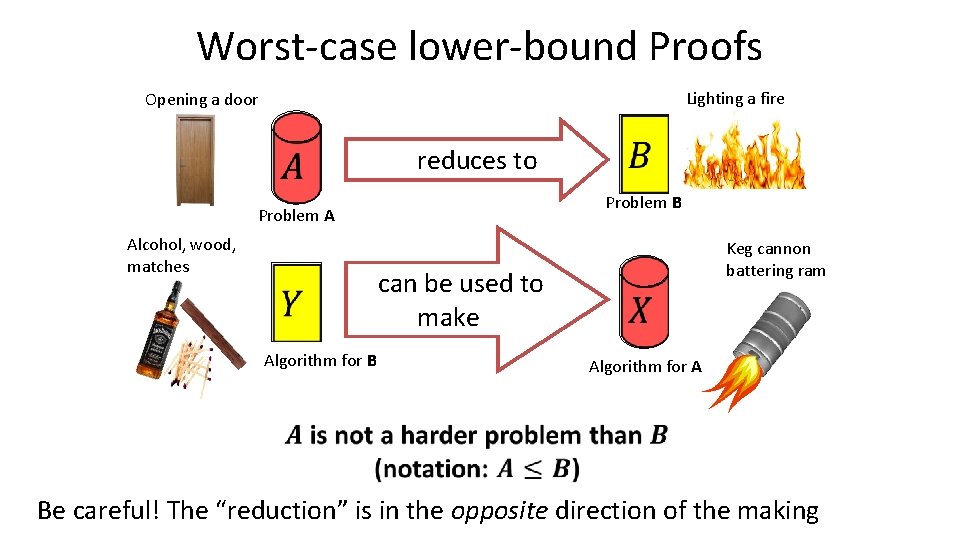
Worst-case lower-bound Proofs Lighting a fire Opening a door reduces to Problem B Problem A Alcohol, wood, matches Keg cannon battering ram can be used to make Algorithm for B Algorithm for A Be careful! The “reduction” is in the opposite direction of the making

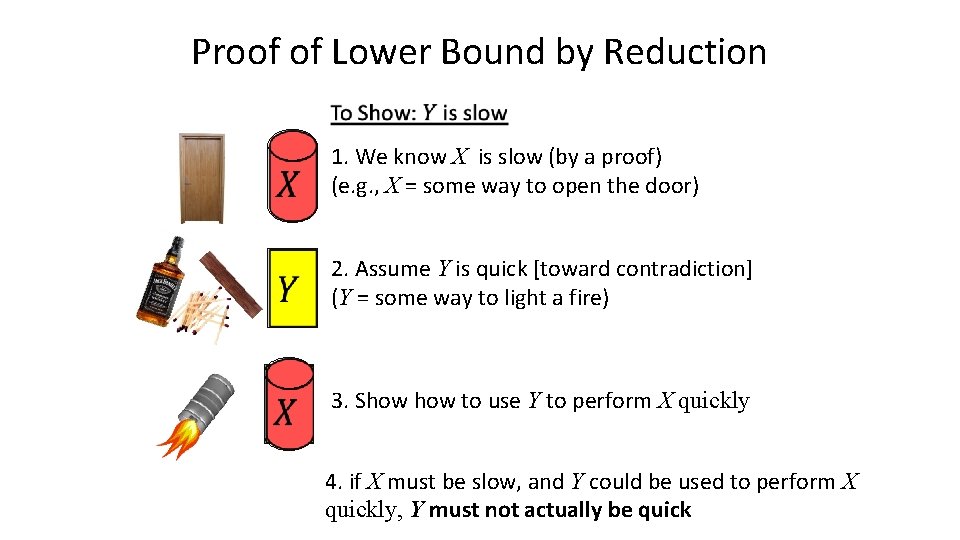
Proof of Lower Bound by Reduction 1. We know X is slow (by a proof) (e. g. , X = some way to open the door) 2. Assume Y is quick [toward contradiction] (Y = some way to light a fire) 3. Show to use Y to perform X quickly 4. if X must be slow, and Y could be used to perform X quickly, Y must not actually be quick

Worst-case Lower-Bound Using Reductions 2 1 • 5 4 6 7 3 8

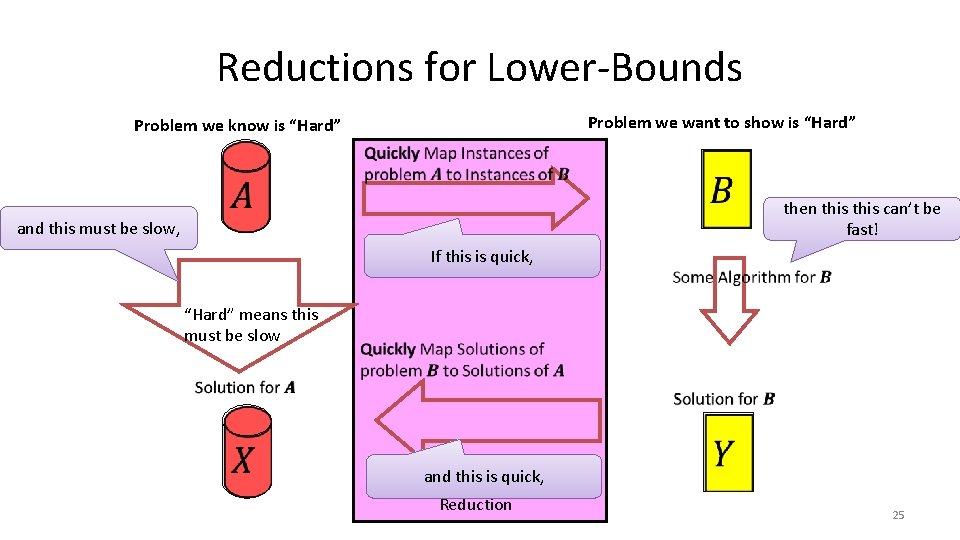
Reductions for Lower-Bounds Problem we want to show is “Hard” Problem we know is “Hard” then this can’t be fast! and this must be slow, If this is quick, “Hard” means this must be slow and this is quick, Reduction 25

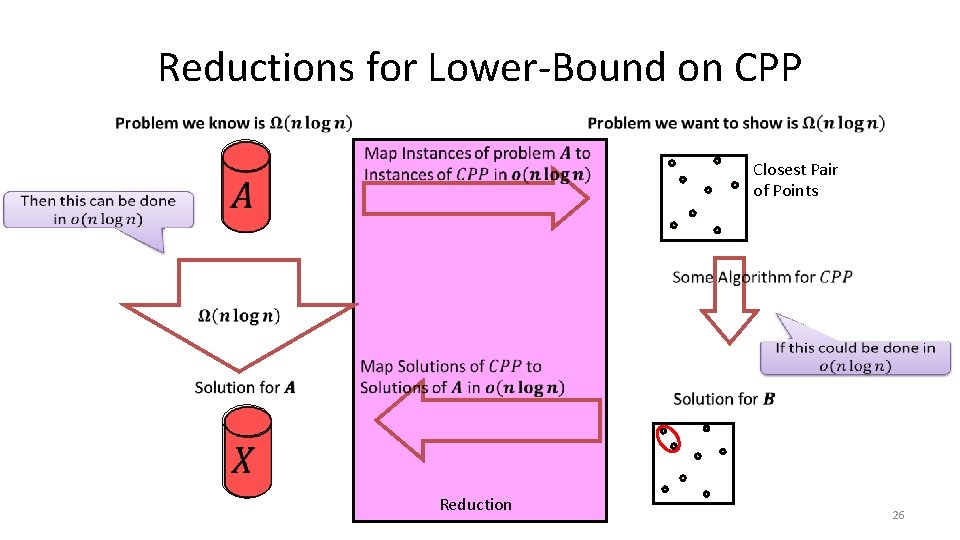
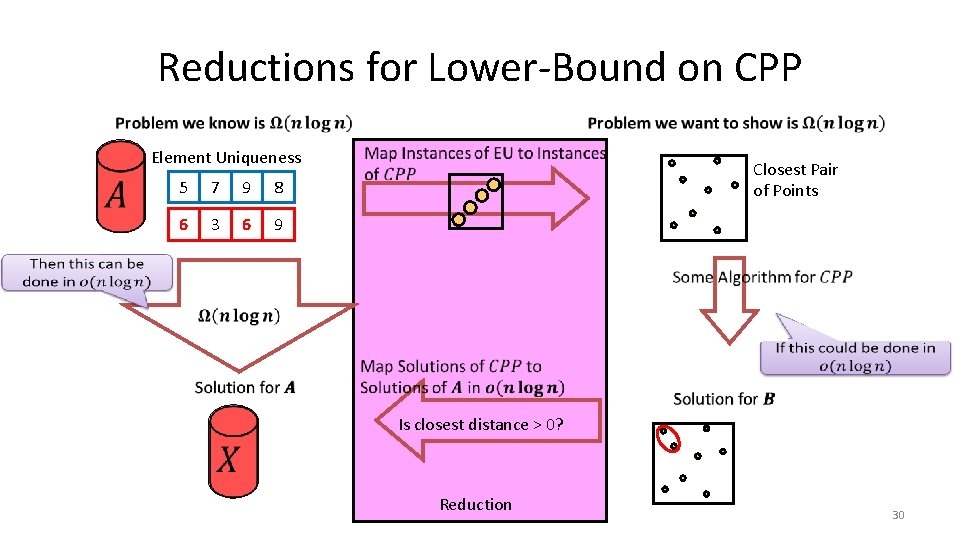
Reductions for Lower-Bound on CPP Closest Pair of Points Reduction 26

A “Hard” Problem: Element Uniqueness • 113 901 555 512 245 800 018 121 True 103 801 401 323 255 323 999 101 False

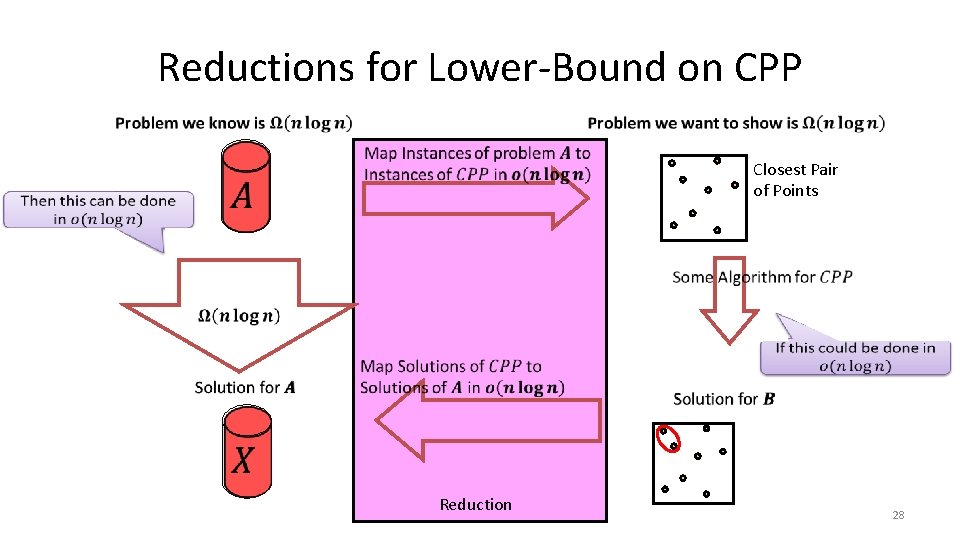
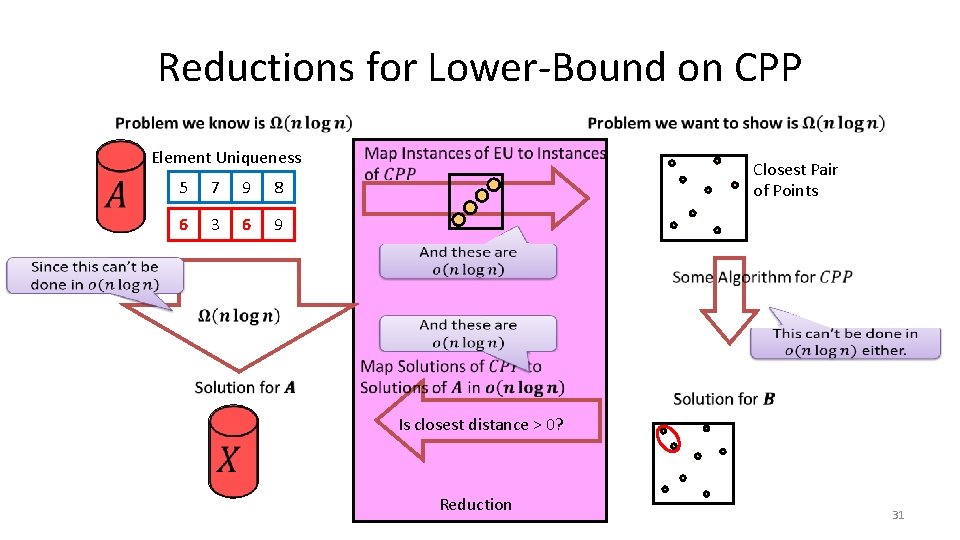
Reductions for Lower-Bound on CPP Closest Pair of Points Reduction 28

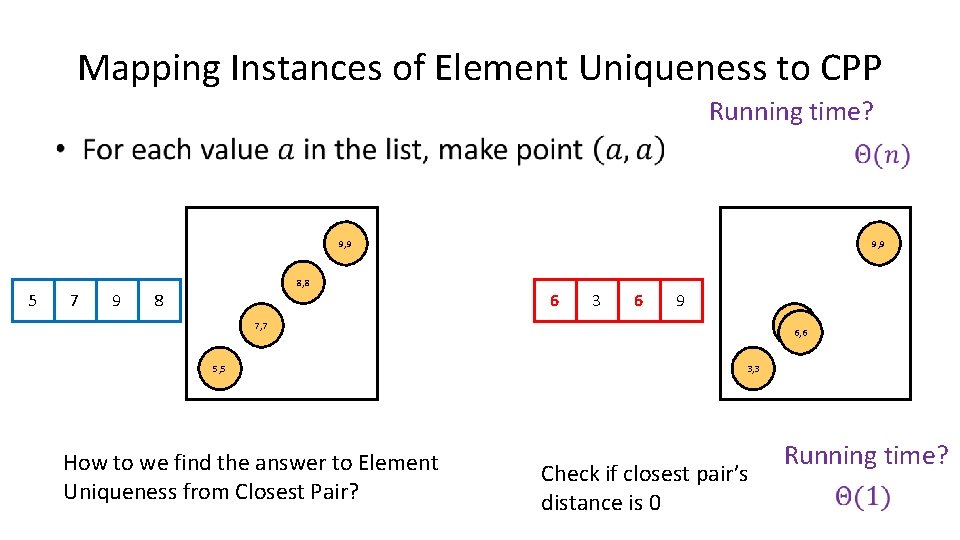
Mapping Instances of Element Uniqueness to CPP Running time? • 9, 9 8, 8 5 7 9 8 6 3 6 9 7, 7 5, 5 How to we find the answer to Element Uniqueness from Closest Pair? 6, 6 3, 3 Check if closest pair’s distance is 0 Running time?

Reductions for Lower-Bound on CPP Element Uniqueness 5 7 9 8 6 3 6 9 Closest Pair of Points Is closest distance > 0? Reduction 30

Reductions for Lower-Bound on CPP Element Uniqueness 5 7 9 8 6 3 6 9 Closest Pair of Points Is closest distance > 0? Reduction 31