CS 4100 Artificial Intelligence Prof C Hafner Class

CS 4100 Artificial Intelligence Prof. C. Hafner Class Notes Feb 14, 2012

Assignment 5 • Why you must re-standardize variables every time a rule is retrieved. • Test data in assignments/A 5 sample. Inputs – easy – average – hard – veryhard

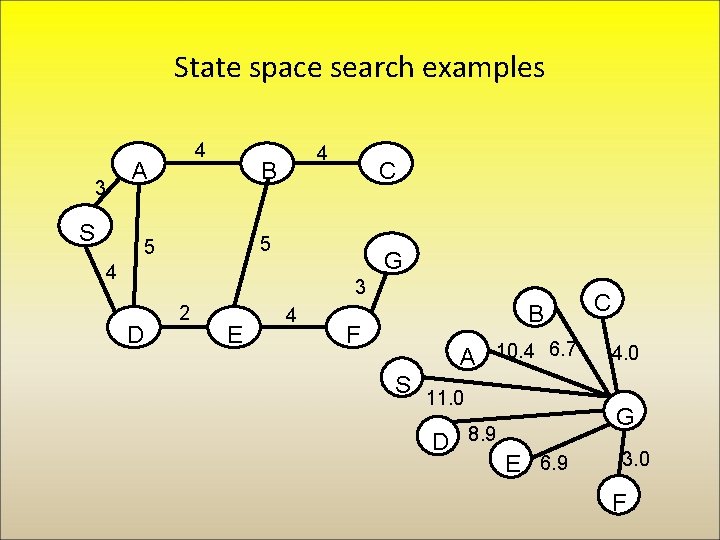
State space search examples 3 4 A S 4 B C 5 5 G 4 3 D 2 E 4 B F A 10. 4 6. 7 S 11. 0 D 8. 9 C 4. 0 G E 6. 9 3. 0 F

New Topic: AI planning • Generating plans • Given: – A way to describe the world (“ontology”) – An initial state of the world – A goal description – A set of possible actions to change the world • Find: – A sequence of actions to change the initial state into one that satisfies the goal • Note similarity to state space search (e. g. , 8 puzzle) • Planning extends to more complex worlds and actions

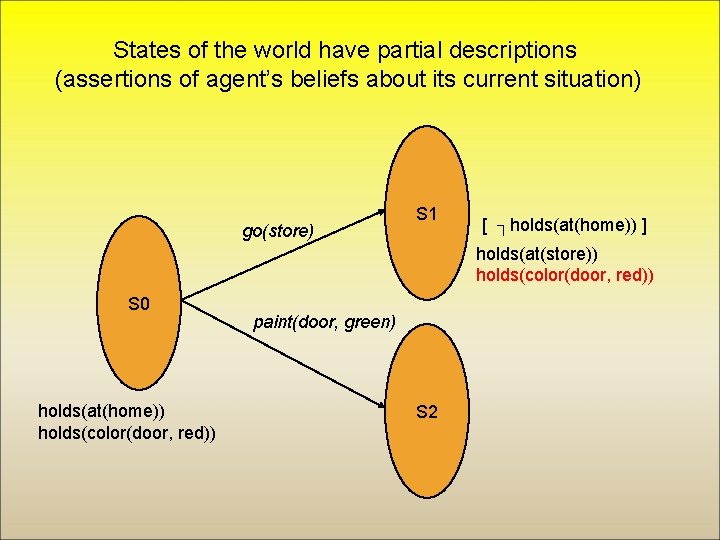
States of the world have partial descriptions (assertions of agent’s beliefs about its current situation) go(store) S 1 [ ┐holds(at(home)) ] holds(at(store)) holds(color(door, red)) S 0 holds(at(home)) holds(color(door, red)) paint(door, green) S 2

Applications • Mobile robots – An initial motivator, and still being developed • Simulated environments – Goal-directed agents for training or games • Web and grid environments – Intelligent Web “bots” – Workflows on a computational grid • Managing crisis situations – E. g. oil-spill, forest fires, urban evacuation, in factories, … • And many more – Factory automation, flying autonomous spacecraft, playing bridge, military planning, …

Plannning challenge: Representing change • As actions change the world OR we consider possible actions, we need to: – Know how an action will alter the world – Keep track of the history of world states (avoid loops) • 3 approaches: – Strips approach with total order planning (state space search) – Strips approach with partial order planning (POP) – Situation calculus

“Classical Planning” Assumptions • Discrete Time – Instantaneous actions • • Deterministic Effects Omniscience Sole agent of change Goals of attainment (not avoidance)

Strips • Highly influential representation for actions: • Instead of F: state X action next state, uses a set of planning operators for achieving goals and subgoals – Preconditions (list of propositions to be true) – Delete list (list of propositions that will become false) – Add list (list of propositions that will become true) – [Implementation] • More efficient to capture known strategies instead of searching the space of possible primitive actions and resulting states.

Example problem: Initial state: at(home), ┐have(beer), ┐have(chips) Goal: have(beer), have(chips), at(home) Operators: Buy (X): Pre: at(store) Add: have(X) Go (X, Y): Pre: at(X) Del: at(X) Add: at(Y)

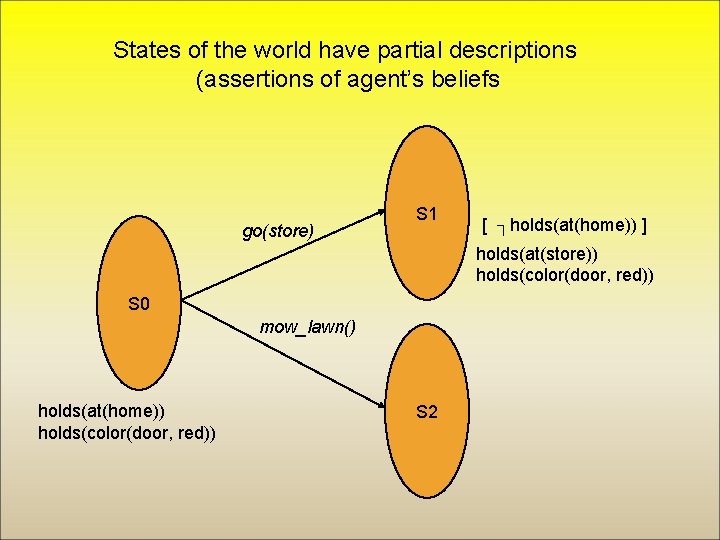
States of the world have partial descriptions (assertions of agent’s beliefs go(store) S 1 [ ┐holds(at(home)) ] holds(at(store)) holds(color(door, red)) S 0 mow_lawn() holds(at(home)) holds(color(door, red)) S 2

Frame problem (again) • I go from home to the store, creating a new situation S’. In S’: – The store still sells chips – My age is still the same – Los Angeles is still the largest city in California… • How can we efficiently represent everything that hasn’t changed? – Strips provides a good solution for simple actions

Another problem: Ramification problem • I go from home to the store, creating a new situation S’. In S’: – I am now in Marina del Rey – The number of people in the store went up by 1 – The contents of my pockets are now in the store. . • Do we want to say all that in the action definition?

Solutions to the frame and ramification problems • In Strips, some facts are inferred within a world state, – e. g. the number of people in the store • All other facts, e. g. at(home) persist between states unless changed (remain unless on delete list) • A challenge for knowledge engineer to avoid mistakes

Questions about Strips • What would happen if the order of goals was at(home), have(beer), have(chips) ? • When Strips returns a plan, is it always correct? efficient? • Can Strips always find a plan if there is one?

Strips operators for blocks world • Move-to (x, b): – Preconditions: Isa(b, Block), On(x, y), Cleartop(x), Cleartop(b) – Add: On(x, b), Cleartop(y) – Delete: On(x, y), Cleartop(b) – Implementation: Puton(x, Topof(b)) • Move-to(x, Table): – Preconditions: – Add: On(x, Table) – Delete: – Implementation: Findspace(x, Table), Puton(x, Table)

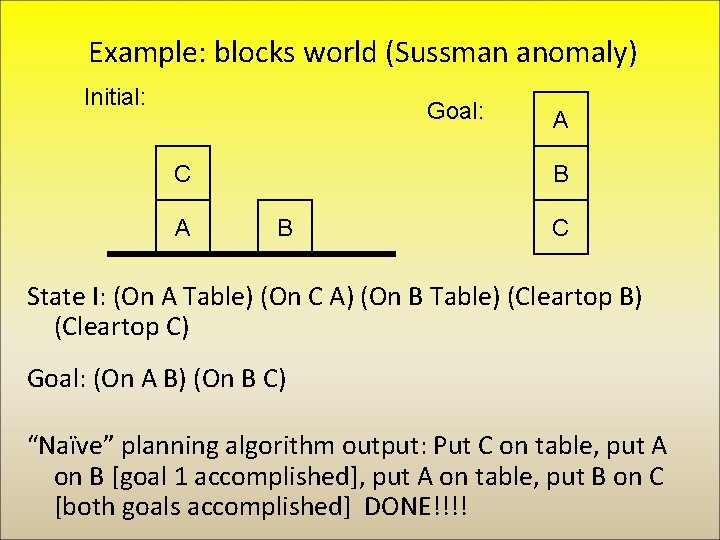
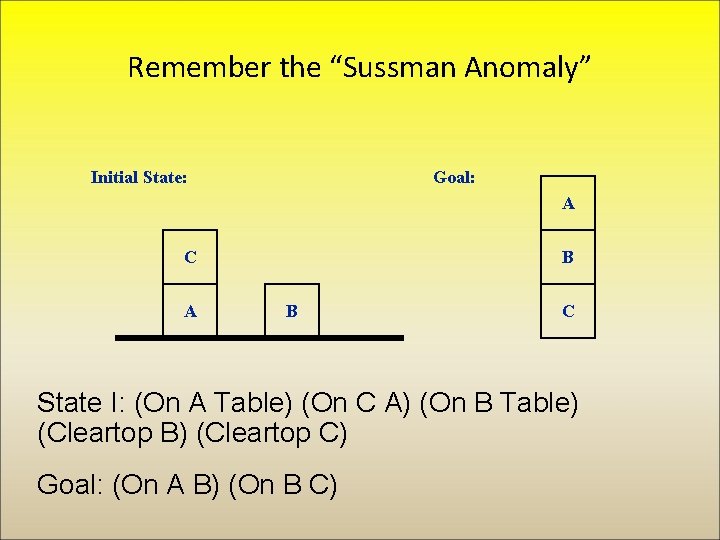
Example: blocks world (Sussman anomaly) Initial: Goal: C A A B B C State I: (On A Table) (On C A) (On B Table) (Cleartop B) (Cleartop C) Goal: (On A B) (On B C) “Naïve” planning algorithm output: Put C on table, put A on B [goal 1 accomplished], put A on table, put B on C [both goals accomplished] DONE!!!!

Partial Order Planning (POP) • Explicitly views plans as a partial order of steps. Add ordering into the plan as needed to guarantee it will succeed. • Avoids the problem in Strips, that focussing on one subgoal forces the actions that resolve that goal to be contiguous.

How to get dressed • State: {} • Goal {Right. Shoe. On, Left. Shoe. On} • Plan Operators: – Put. Rshoe, Precond: Right. Sock. On, Effect: Right. Shoe. On – Put. Lshoe, Precond: Left. Sock. On, Effect: Left. Shoe. On – Put. Rsock, Effect: Right. Sock. On – Put. Lsock, Effect: Left. Sock. On • Create a POP graph of solutions with causal links: p “A achieves P for B” A B (also called protection links). This prevents another goal from causing a sock to be removed before the shoe goes on.

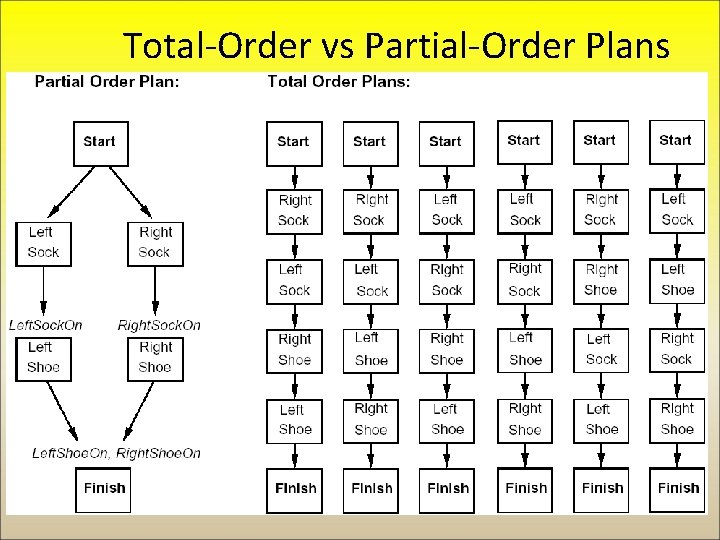
Total-Order vs Partial-Order Plans

Remember the “Sussman Anomaly” Initial State: Goal: A C A B B C State I: (On A Table) (On C A) (On B Table) (Cleartop B) (Cleartop C) Goal: (On A B) (On B C)

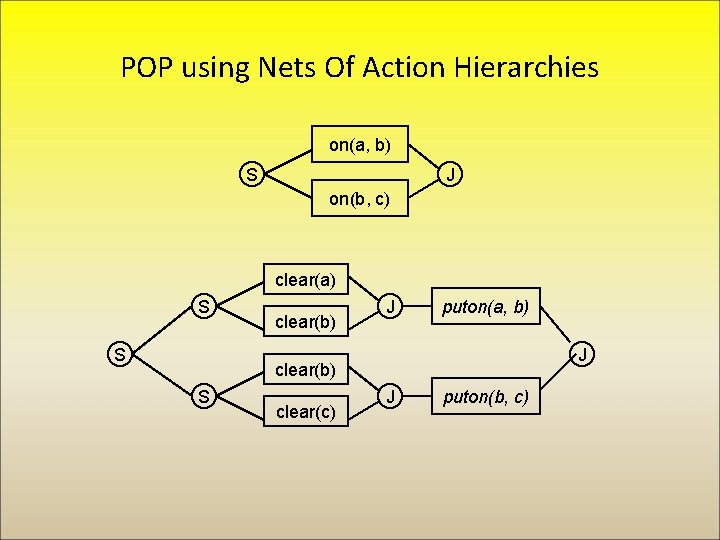
POP using Nets Of Action Hierarchies on(a, b) S J on(b, c) clear(a) S S clear(b) J puton(a, b) J clear(b) S clear(c) J puton(b, c)

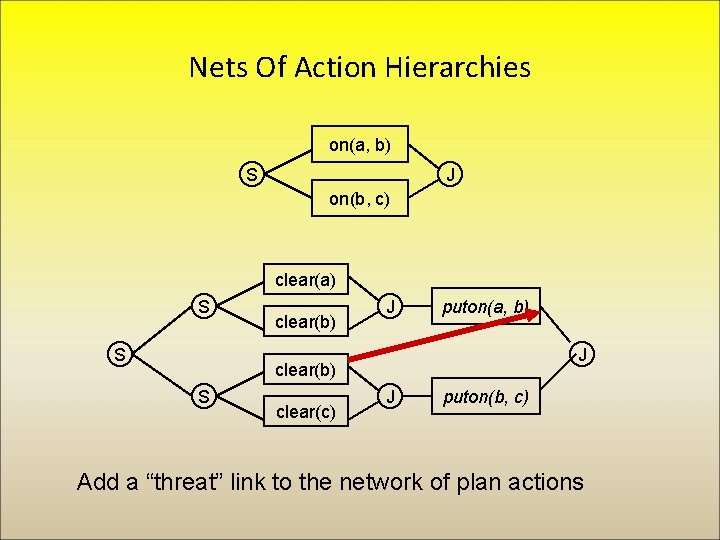
Nets Of Action Hierarchies on(a, b) S J on(b, c) clear(a) S S clear(b) J puton(a, b) J clear(b) S clear(c) J puton(b, c) Add a “threat” link to the network of plan actions

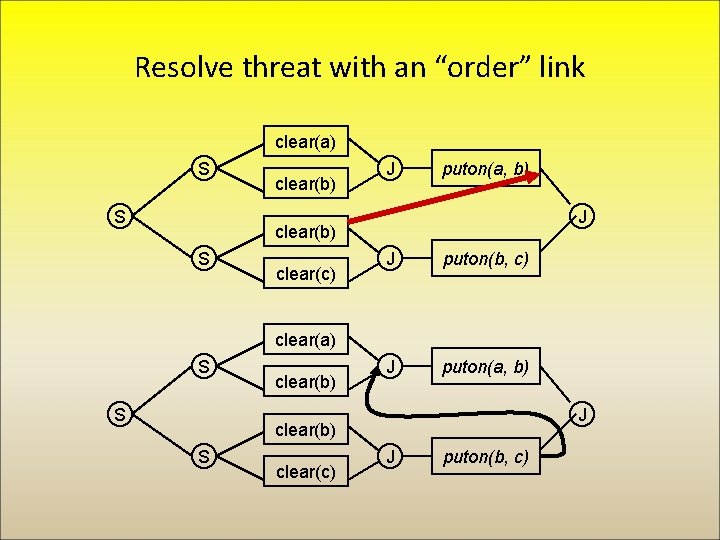
Resolve threat with an “order” link clear(a) S S clear(b) J puton(a, b) J clear(b) S clear(c) J puton(b, c) J puton(a, b) clear(a) S S clear(b) J clear(b) S clear(c) J puton(b, c)

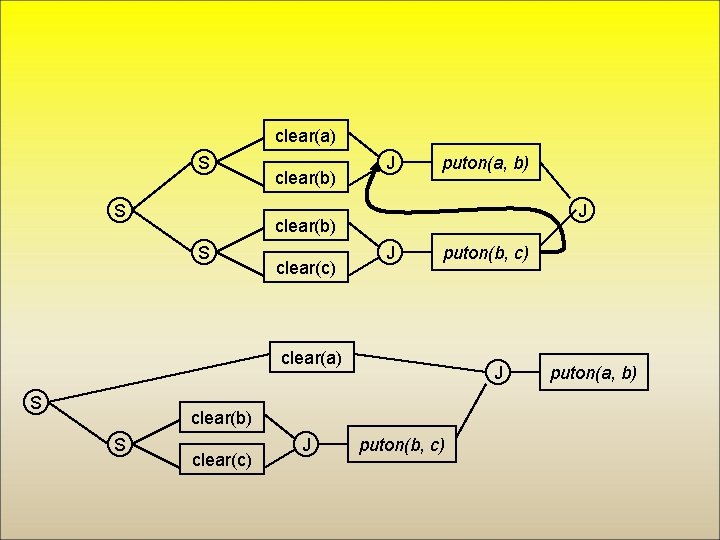
clear(a) S S clear(b) J puton(a, b) J clear(b) S clear(c) J puton(b, c) clear(a) S J clear(b) S clear(c) J puton(b, c) puton(a, b)

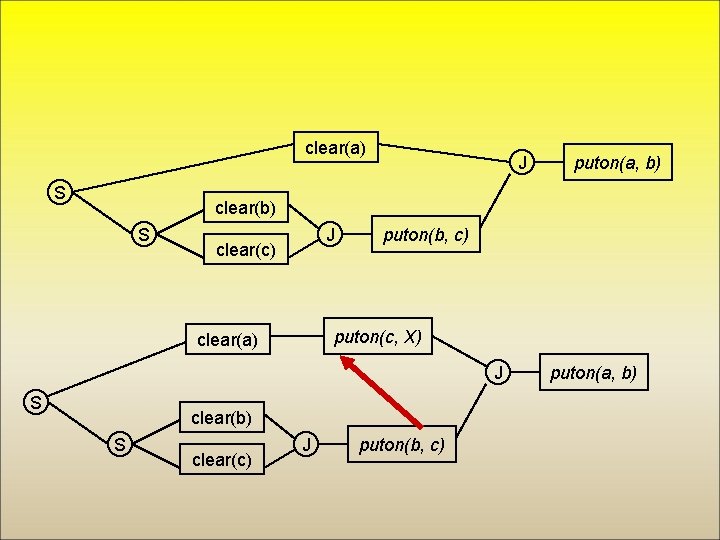
clear(a) S J puton(a, b) clear(b) S J clear(c) puton(b, c) puton(c, X) clear(a) J S clear(b) S clear(c) J puton(b, c) puton(a, b)

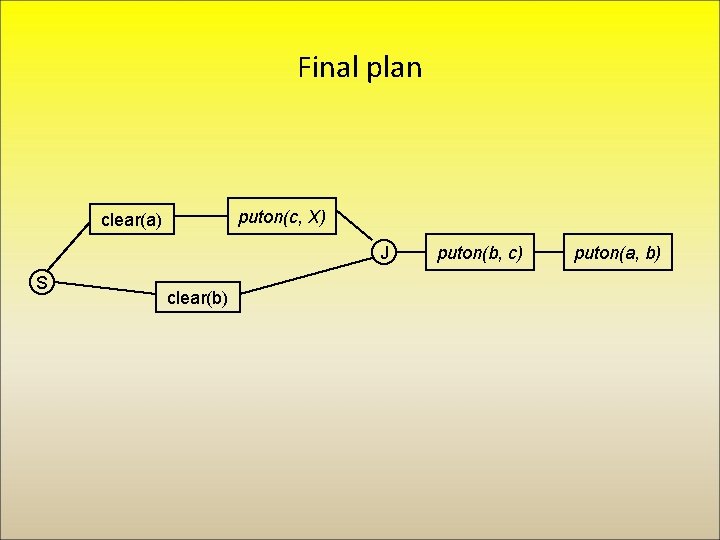
Final plan puton(c, X) clear(a) J S clear(b) puton(b, c) puton(a, b)

Planning using logic and resolution: The situation calculus • Key idea: represent a snapshot of the world, called a ‘situation’ explicitly. • ‘Fluents’ are statements that are true or false in any given situation, e. g. ‘I am at home’ • Actions map situations to situations.

Blocks world example • A move action: Move(x, loc) • Use of the Result function: Result(Move(x, loc), state) the state resulting from doing the Move action • An axiom about moving: x loc s [ At(x, loc, Result(Move(x, loc), s)) ] “If you move some object to a location, then in the resulting state that object is at that location • At(B 1, Table, S 0) • At(B 1, Top(B 2), Result(Move(B 1, Top(B 2)), S 0)) using the axiom

Monkeys and Bananas Problem • The monkey-and-bananas problem is faced by a monkey standing under some bananas which are hanging out of reach from the ceiling. There is a box in the corner of the room that will enable the monkey to reach the bananas if he climbs on it. • Use situation calculus to represent this problem and solve it using resolution theorem proving.

Representation of Monkey/Banana problem • Fluents: – At(x, loc, s) – On(x, y, s) – Reachable(x, Bananas, s) – Has(x, y, s) • Other predicates – Moveable(x), Climbable(x) – Can-move(x) • Actions – Climb-on(x, y) – Reach(x, y) Constants: - BANANAS - MONKEY - BOX - S 0 - CORNER - UNDER-BANANAS -- Move(x, loc) -- Push(x, y, loc)

Monkey/Bananas axioms 1. ∀ x 1, s 1 [ Reachable(x 1, BANANAS, s 1) Has(x 1, BANANAS, Result(Reach(x 1, BANANAS), s 1)) ] If a person can reach the bananas then the result of reaching them is to have them. 2. ∀ s 2 [At(BOX, UNDER-BANANAS, s 2) ^ On(MONKEY, BOX, s 2) Reachable(MONKEY, BANANAS, s 2) If a box is under the bananas and the monkey is on the box then the monkey can reach the bananas.

Monkey/Bananas axioms 3. ∀ x 3, loc 3, s 3 [ Can-move(x 3) At(x 3, loc, Result(Move(x 3, loc 3), s 3)) ] The result of moving to a location is to be at that location 4. ∀ x 4, y 4, s 4 [∃ loc 4 [At(x 4, loc 4, s 4) ^ At(y 4, loc 4, s 4)] ^ Climbable(y 4) On(x 4, y 4, Result(Climb-on(x 4, y 4), s 4))] The result of climbing on an object is to be on the object 5. ∀ x 5, y 5, loc 5, s 5 [∃ loc [At(x, loc 0, s) ^ At(y 5, loc 0, s 5) ] ^ Moveable(y 5) At(y 5, loc 5, Result(Push(x 5, y 5, loc 5), s 5)) 6. <same> At(x 6, loc 6, Result(Push(x 6, y 6, loc 6), s 6)) ] The result of x pushing y to a location is both x and y are at that location.

Monkey/Bananas axioms (initial state S 0) F 1. Moveable(BOX) F 2. Climbable(BOX) F 3. Can-move(MONKEY) F 4. At(BOX, CORNER, S 0) F 5. At(MONKEY, UNDER-BANANAS, S 0) • To solve this for the goal Has(MONKEY, BANANAS, s): – Convert to clause form – Apply resolution to prove something like this: Has(MONKEY, BANANAS, Result(Reach(. . . ), Result(. . ), S 0) which gives you the plan in reverse order. (don’t forget to standardize!) We need 2 additional “frame axioms” for the proof

Frame Axioms for Monkey/Bananas world 7. ∀ x, y, loc, s [ At(x, loc, s) At(x, loc, Result(Move(y, loc), s)) ] The location of an object does not change as a result of someone moving to the same location. 8. ∀ x, y, loc, s [ At(x, loc, s) At(x, loc, Result(Climb-on(y, x), s)) ] The location of an object does not change as a result of someone climbing on it.

Refutation Resolution as theoretical basis of BC A query is conceptualized with existential variables: ? Likes(John, x) means ? ∃x Likes(John, x) to answer the question, assert its NEGATION, and attempt to derive a contradiction by RESOLVING TO THE EMPTY CLAUSE! ~ ∃x Likes(John, x) is equivalent to ∀ x ~ Likes(John, x), so add that to the KB and try to derive the empty clause Resolution rule: [A 1 V A 2 V. . . An] ^ [B 1 V B 2 V. . Bm V ~A 1’] where A 1 and A 1’ unify -------------------------------[ A 2’ V. . . An’ ] ^ [B 1’ V B 2’ V. . . Bm’] Likes(John, Pizza) ^ ~ Likes(John, x) resolves to { }, given {x/Pizza}

A Limitation of Situation Calculus: The Frame problem • I go from home (S) to the store, creating a new situation S’. In S’: – My friend is still at home – The store still sells chips – My age is still the same – Los Angeles is still the largest city in California… • How can we efficiently represent everything that hasn’t changed?

Successor state axioms • Normally, things stay true from one state to the next -unless an action changes them: At(p, loc, Result(a, s)) iff a = Go(p, x) or [At(p, loc, s) and a != Go(p, y)] • We need one or more of these for every fluent • Now we can use theorem proving (or possibly backward chaining) to deduce a plan: not very practical