CS 4100 Artificial Intelligence Prof C Hafner Class

















































- Slides: 60

CS 4100 Artificial Intelligence Prof. C. Hafner Class Notes Jan 26, 2012

Topics • More about assignment 3 • Negation by failure and Horn Clause databases – Closed world assumption • First order logic continued • Wumpus world model using FOL Jan 31 • A few more details about hw 3 – Test data available – load. Initial. KB and process. Percepts functions • • Return an discuss assignments 1 and 2 Converting FOL sentences to Normal Form Unification Automated reasoning in FOL: resolution, forward chaining, backward chaining

Sketch of Forward Chaining Algorithm (version 1 assumes the initial KB is fully expanded) ALGORITHM (recursive): process. Percepts(‘percepts file’) uses KBase -- a knowledge base of definite clauses for each new percept p PLForward. Chain(p) #use a recursive "helper function" PLForward. Chain(percept) if percept is already in KBase, return else add percept to KBase for r in rules where conclusion of r is not already in KBase if percept is a premise of r and all the other premises of r are known PLForward. Chain(conclusion of r)

Sketch of Forward Chaining Algorithm (version 2 drops this assumption) process. Percepts(‘percepts file’) uses KBase -- a knowledge base of definite clauses for each new percept p PLForward. Chain(p) #use a recursive "helper function" PLForward. Chain(percept) if percept is already in KBase, return else add percept to KBase for r in rules where conclusion of r is not already in KBase if percept is a premise of r and all. True(premises of r) #all premises are known or provable PLForward. Chain(conclusion of r) all. True(premises) for p in premises if p is already in Kbase continue if p is not provable return false return true

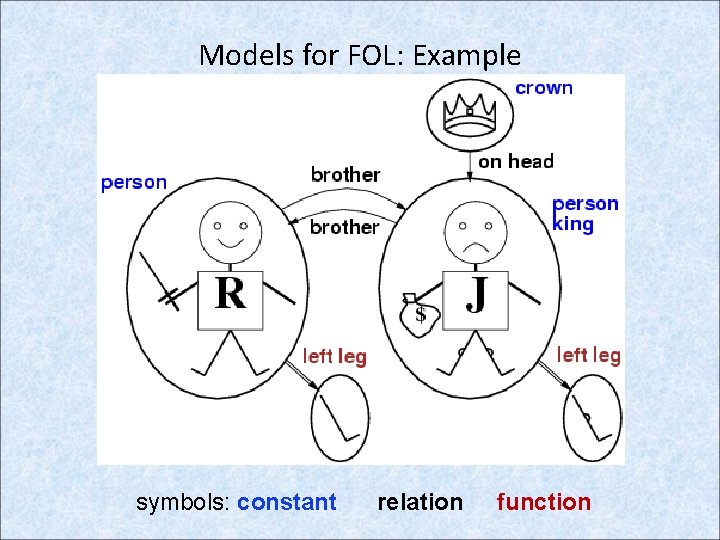
Return to FOL: Meaning and truth (review) • Sentences of FOL are true with respect to a model and an interpretation • A model for a FOL language is a “world” of objects (domain elements) and relations among them (compare with propositional logic model) • Interpretation I specifies referents for constant symbols → objects predicate symbols → relations function symbols → functions • For an atomic sentence, the interpretation I(P(term 1, . . . , termn) )= true iff the objects I(term 1). . . , I(termn) are in the relation I(P)

Meaning and truth in first-order logic (cont. ) • Complex sentences: truth is defined using the same truth tables: I(S 1 S 2) = true iff I (S 1) = true and I (S 2) = true. • I( x [S]) = true iff for every object o in the model I (S[x/C]) = true when. I (C) = o • I( x [S]) = is true iff there is at least one object o in the model such that: I (S[x/C]) = true when. I (C) = o

Models for FOL: Example symbols: constant relation function

Quantification examples: • <variables> <sentence> Everyone at NU is smart: x [ At(x, NU) Smart(x) ] • x P is true in a model m iff P is true with x being each possible object in the model • Roughly speaking, equivalent to the conjunction of all instantiations of P At(King. John, NU) Smart(King. John) At(Richard, NU) Smart(Richard) At(NUS, NU) Smart(NUS)

A common mistake to avoid • Typically, is the main connective with • Common mistake: using as the main connective with : x At(x, NU) Smart(x) means “Everyone is at NU and everyone is smart”

Quantification examples (cont. ) • <variables> <sentence> • Someone at NU is smart: • x [At(x, NU) Smart(x)] • x P is true in a model m iff P is true with x being some possible object in the model • Roughly speaking, equivalent to the disjunction of all instantiations of P At(King. John, NU) Smart(King. John) At(Richard, NU) Smart(Richard) At(NU, NU) Smart(NU) . . .

Another common mistake to avoid • Typically, is the main connective with • Common mistake: using as the main connective with : x At(x, NU) Smart(x) is true if there is no one who at NU!

• • Properties of quantifiers x y is the same as y x x y is not the same as y x x y Loves(y, x) – “There is a person who is loved by everyone in the world” • x y Loves(y, x) – “Everyone in the world is loved by at least one person” • Quantifier duality: each can be expressed using the other(cf De. Morgan laws) • x Likes(x, Ice. Cream) == x Likes(x, Ice. Cream) • x Likes(x, Broccoli) == x Likes(x, Broccoli)

Equality • term 1 = term 2 is true under a given interpretation if and only if term 1 and term 2 refer to the same object • E. g. , definition of Sibling in terms of Parent: x, y Sibling(x, y) [ (x = y) m, f [ (m = f) Parent(m, x) Parent(f, x) Parent(m, y) Parent(f, y)]] • We will use a different notation for equality: =(x, y) – makes programming simpler

A model M for the kinship domain • Individuals: J K L M N O P Q R • Functions: mom[1] : mom(N) M • Relations[arity] – fem[1] = {M, Q} – par[2] = {[M, N], [N, R]. . } – sib[2] = {[M, O], [P, J], [J, P]} ----------Interpretation I ----------- • Constants: John, Mary, Sue, Tom. . – I(Mary) = M, I(Sue) = Q, . . . • Function symbol: Mother, I(Mother) = mom • Relation symbols: Female, Parent, Sibling I(Female) = fem, I(Parent) = par, I(Sibling) = sib

Using FOL The kinship domain: • Brothers are siblings x, y Brother(x, y) Sibling(x, y) • “Sibling” is symmetric x, y Sibling(x, y) Sibling(y, x) • One's mother is one's female parent m, c =(Mother(c) , m) (Female(m) Parent(m, c)) • Some mothers are over 40 years old m, x [=(Mother(x), m) ^ > (Age(m), 40) ]

Knowledge Engineering: Choice of Representations • Human(Bob) vs. ISA(Bob, Human) • Green(B 21) vs. Color(B 21, Green) The choice affects the generality at which concepts can be expressed Inheritance rule: x, y, z ISA(x, y) ^ ISA(y, z) ISA(x, z) Two blocks are the same color: x Color(B 21, x) ^ Color(B 22, x)

Informal quiz on use of FOL to represent “common sense” knowledge • • • All apples are red Some apples are red (“some” means at least one) All apples contain (some) worms Some apples contain (some) worms Every person is mortal Every person is male or female (but not both)

Wumpus world in FOL • First step: define constants, function symbols, predicate symbols to express the facts • Percept(data, t) means: at step t, the agent perceived the data where data is a vector: – [Stench, Breeze, Glitter] – Ex: Percept([None, Breeze, None], 2] • At(Agent, s, t) means: agent is at square s at step t – Ex: At(Agent, [2, 1], 2]

Some Wumpus axioms Axiom to interpreting perceptions in context x, t At(Agent, x, t) ^ Breeze(t) Breezy(x) Definitional axiom: s, g, t Percept([s, Breeze, g], t) Breeze(t) Diagnostic Axiom x Breezy(x) z Adjacent(z, x) ^ Pit(z) Causal Axiom: z Pit(z) ( x Adjacent(z, x) Breezy(x)) World model axioms: Adjacent([1, 1], [2, 1]) etc. x, y Adjacent(x, y) Adjacent(y, x)

Interacting with FOL KBs • Suppose a wumpus-world agent is using an FOL KB and perceives a smell and a breeze (but no glitter) at t=5: Tell(KB, Percept([Smell, Breeze, None], 5)) – use forward chaining Ask(KB, a Best. Action(a, 5)) - use backward chaining BC Query: does the KB entail some best action at t=5? • Answer: {a/Shoot} ← substitution (binding list) • Given a sentence S and a substitution σ, • Sσ denotes the result of plugging σ into S; e. g. , S = Smarter(x, y) σ = {x/Sue, y/Bill} Sσ = S {x/Sue, y/Bill} = Smarter(Sue, Bill) • Ask(KB, S) returns σ such that KB╞ Sσ

Knowledge engineering in FOL 1. Identify the task 1. Assemble the relevant knowledge 2. Decide on a vocabulary of predicates, functions, and constants (a logical language L) 3. Encode general knowledge about the domain 4. Encode a description of the specific problem instance 5. Pose queries to the inference procedure and get answers 5. Debug the knowledge base

Negation by failure and CWA A closed world is a world where every fact that is not known is false. Real-world examples: databases Query: Does American Airlines fly from Boston to Tampa? If no DB records of such flights answer NO (consider a Horn clause KB of food “likes”) Query: Does Sam like cheeseburgers? not a known “fact” not provable by “rules”

Conversion to CNF • Everyone who loves all animals is loved by someone: x [ y [Animal(y) Loves(x, y)] y Loves(y, x) ] • 1. Eliminate biconditionals and implications x [ y [ Animal(y) Loves(x, y) ] y Loves(y, x) ] • 2. Move inwards: x p ≡ x p, x p ≡ x p x [ y [ ( Animal(y) Loves(x, y))] y Loves(y, x) ] x [ y [Animal(y) Loves(x, y) ] y Loves(y, x) ] No more negated quantifiers

Conversion to CNF contd. 3. Rename variables: each quantifier should use a different one x [ y [Animal(y) Loves(x, y) ] y Loves(y, x) ] x 1 [ y 1 [ Animal(y 1) Loves(x 1, y 1) ] y 2 Loves(y 2, x 1) ] 4. Skolemize: Each existential variable is replaced by a Skolem function of the enclosing universally quantified variables: x 1 [ (Animal(F 1(x 1)) Loves(x 1, F 1(x 1))) Loves(F 2(x 1), x 1) ] 5. Drop universal quantifiers: (Animal(F 1(x)) Loves(x, F 1(x))) Loves(F 2(x), x) 3. Distribute over Animal(F 1(x)) Loves(F 2(x), x) Loves(x, F 1(x) ) Loves(F 2(x), x)

Class exercise

Inference in FOL – Chapter 9 • Theoretical foundations – Inference by universal and existential instantiation – Unification – Resolution viewed as Generalized Modus Ponens • Practical implementation (forward and backward chaining)

Notation A substitution is a set of variable-term pairs: {x/term, y/term, . . . }, often referred to using the symbol θ [theta]. No variable can occur more than once. For any term or formula A: Subst(θ, A) also written Aθ == the result of replacing each variable in A with the corresponding term. A term is a constant symbol, a variable symbol, or a function symbol applied to 0 or more terms. Def: A ground term is a term with no variables Def: A ground sentence is a sentence with no free variables

Inference by Universal instantiation (UI) • Every instantiation of a universally quantified sentence is entailed by it: v α Subst({v/g}, α) for any variable v and ground term g • E. g. , x King(x) Greedy(x) Evil(x) yields: King(John) Greedy(John) Evil(John) King(Richard) Greedy(Richard) Evil(Richard) King(Father(John)) Greedy(Father(John)) Evil(Father(John)).

Inference by Existential instantiation (EI) • For any sentence α, variable v, and constant symbol k that does not appear elsewhere in the knowledge base: v α Subst({v/k}, α) • E. g. , x Crown(x) On. Head(x, John) yields: Crown(C 1) On. Head(C 1, John) provided C 1 is a new constant symbol, called a Skolem constant

To implement universal instantiation • All humans are mortal • Jack is human -------------- • Jack is mortal R 1. x Human(x) Mortal(x) F 1. Mortal(Jack) Let R 1 be p q, Let F 1 be be p’ Modus ponens for FOL: If p and p’ unify, conclude q’ Unify means we can match p and p’ by a substitution. We then apply the same substitution to q to get q’

Unification • Def: Two formulas A and B unify if there is a substitution θ such that Aθ = Bθ. • Ex: To unify A = Knows(John, x) and B = Knows(y, Mary) θ = {y/John, x/Mary } • θ is not unique! • To unify A = Knows(John, x) and B = Knows(y, z), θ 1 = {y/John, x/z } or θ 2 = {y/John, x/Sue, z/Sue} • The first unifier is more general than the second. • There is a single most general unifier (MGU) that is unique up to renaming of variables. MGU = { y/John, x/z } or {y/John, z/x }

Most general unifier • Def: If θ 1 is a unifier formulas A and B, it is a MOST GENERAL UNIFIER (MGU) iff: – There is no other unifier θ 2 for A and B such that Aθ 1 subsumes Aθ 2 • A formula F subsumes a formula G if there is a nontrivial substitution such that F = G • A θ 1 = Knows(John, z) Aθ 2 = Knows(John, Sue) Aθ 1 subsumes Aθ 2 therefore θ 2 = {y/John, x/Sue, z/Sue} is not a MGU. Note: what is ? ?

Class Exercise: Unification Examples Unify(α, β) = θ if αθ = βθ p Knows(John, x) q Knows(John, Jane) Knows(y, Barak) Knows(y, Mother(y)) Knows(x, Barak) θ

Unification • Unify(α, β) = θ if αθ = βθ p q Knows(John, x) Knows(John, Jane) Knows(John, x) Knows(y, Barak) Knows(John, x) Knows(y, Mother(y)) Knows(John, x) Knows(x, Barak) θ {x/Jane}}

Unification • Unify(α, β) = θ if αθ = βθ p q Knows(John, x) Knows(John, Jane) Knows(John, x) Knows(y, Barak) Knows(John, x) Knows(y, Mother(y)) Knows(John, x) Knows(x, Barak) θ {x/Jane}} {x/Barak, y/John}}

Unification

Unification

The unification algorithm (Fig. 9. 1)

The unification algorithm (cont. )

Application to reasoning Modus ponens says: Given p q and p Conclude: q In FOL: Given p q and p’ (where p and p’ unify by θ) Conclude: qθ Suppose KB includes: x King(x) Greedy(x) Evil(x) King(John) This won’t quite work since we have p 1 ^ p 2 q

Generalized Modus Ponens (GMP) (follows from the resolution rule for FOL) ( p 1 p 2 … pn q), p 1', p 2', … , pn' qθ p 1' is King(John) p 2' is Greedy(y) θ is {x/John, y/John} where pi'θ = pi θ for all i p 1 is King(x) p 2 is Greedy(x) q is Evil(x) q θ is Evil(John) • GMP used with KB of definite clauses (exactly one positive literal) • All variables assumed universally quantified • How do we get Greedy(y) in our KB ?

Soundness of GMP • Need to show that p 1', …, pn', (p 1 … pn q) ╞ qθ provided that pi'θ = piθ for all p • Lemma: For any sentence p, we have p ╞ pθ by UI 1. (p 1 … pn q) ╞ (p 1 … pn q)θ = (p 1θ … pnθ qθ) – p 1', …, pn' ╞ (p 1' … pn‘ ) θ ╞ p 1'θ … pn'θ – From 1 and 2, qθ follows by ordinary Modus Ponens Note: you should know the definitions of a sound inference procedures and a complete inference procedure.

Forward Chaining in FOL (with the “explicit knowledge” assumption) • Assume percepts do not contain variables (may contain “generated symbol” constants) • Example: you see an unfamiliar dog in the building: Percept: Isa(G 33, Dog) Assume KB includes: Isa(x, Dog) Isa(x, Animal) • Add new percept to KB if not already believed • If percept UNIFIES with a rule premise (by some θ) and if all the other premises pθ are believed, add qθ to KB. • θ is {x/G 33) and qθ is isa(G 33, Animal)

Backward Chaining • Given a definite clause KB and a query q’: – For any fact q in KB that unifies with q’, return θ (or “YES” if θ = { } ) – For any rule in KB whose conclusion q unifies with q’: • If the rule’s premises p 1 θ. . . pn θ can all be proved with a resulting substitution θ’, return COMPOSE(θ, θ’) – If no facts or rules result in a substitution, return “NO” • Note this can return multiple answers!

Simple examples • KB: Likes(John, Pizza) Likes(Mary, Pizza) Likes(Sam, Ice. Cream) • Query: Likes(John, Pizza) return YES • Query: Likes(Sam, Pizza) return NO (justified by CWA) • Query: Likes(x, Pizza) return a list of substitutions { {x/John} , {x/Mary} }

More complex examples • Add to KB: Likes(y, Pizza) Likes(y, Spaghetti) • Query: Likes(John, Spaghetti) • Query: Likes(Sam, Spaghetti) • Query: Likes(x, y) Set of substitutions: { {x/John, y/Pizza}, {x/Mary, y/Pizza}, {x/Sam, y/Ice. Cream}, {x/John, y/Spaghetti}, {x/Mary, y/Spaghetti} }

Backward chaining algorithm SUBST(COMPOSE(θ 1, θ 2), p) = SUBST(θ 2, SUBST(θ 1, p))

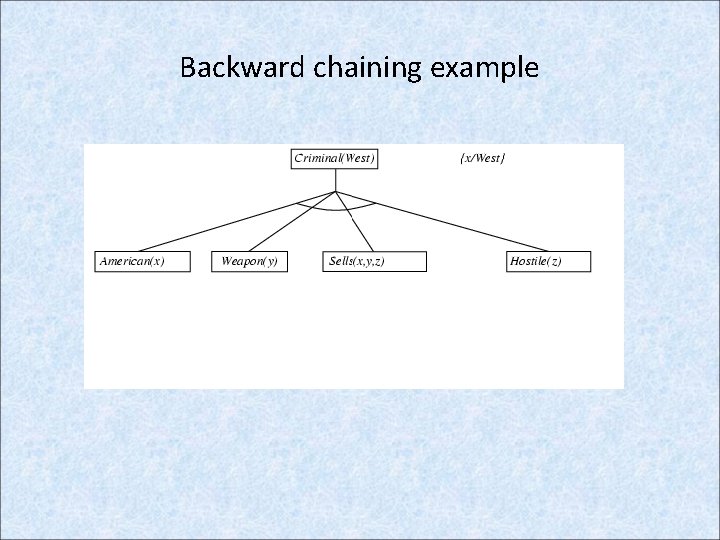
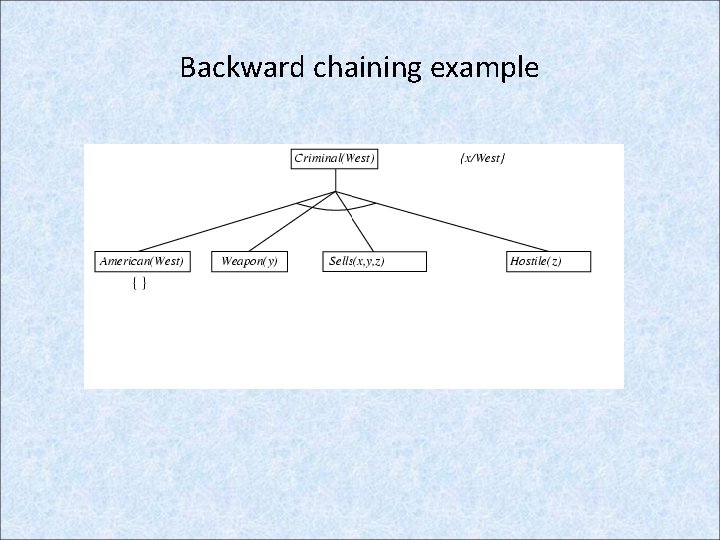
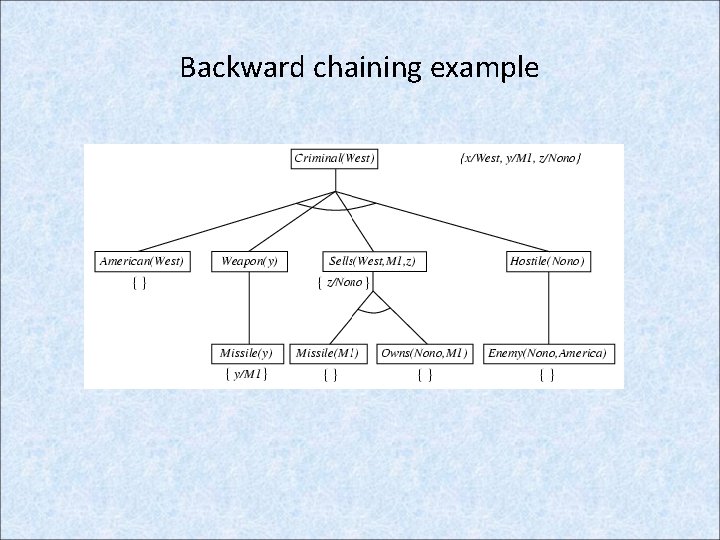
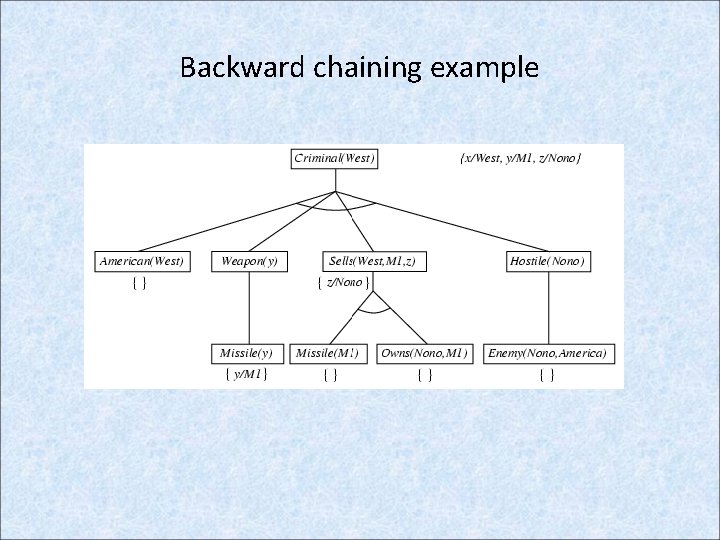
Backward Chaining: Example knowledge base • The law says that it is a crime for an American to sell weapons to hostile nations. The country Nono, is an enemy of America, has some missiles, and all of its missiles were sold to it by Colonel West, who is American. • Prove that Col. West is a criminal

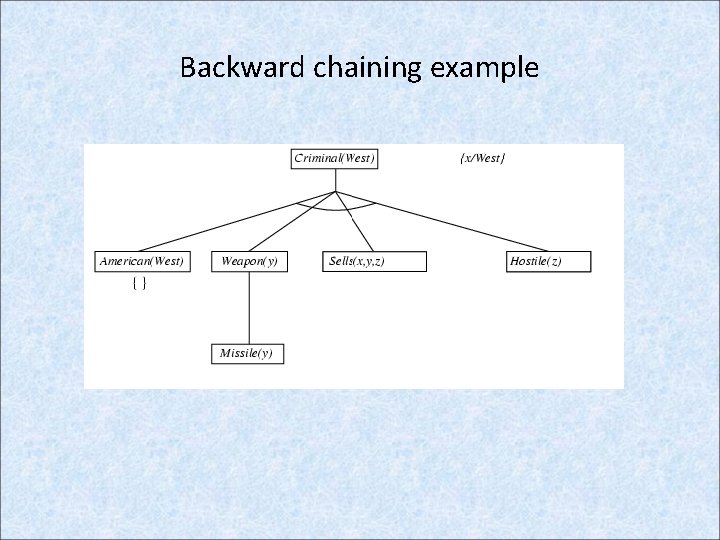
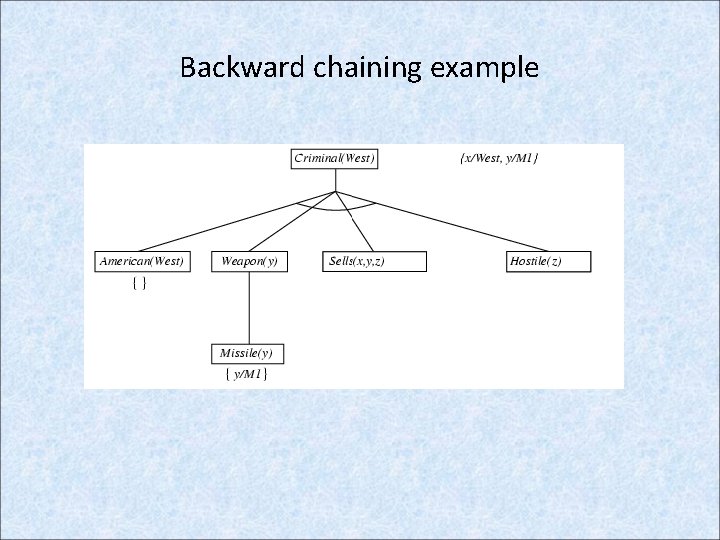
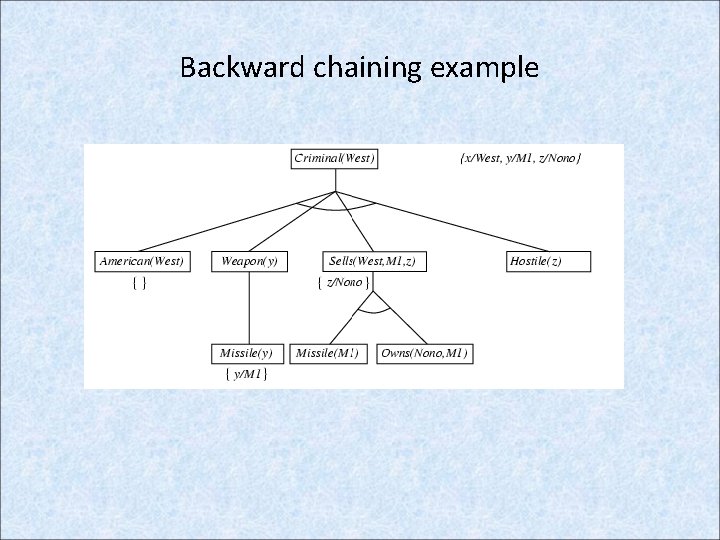
Example knowledge base contd. . it is a crime for an American to sell weapons to hostile nations: American(x) Weapon(y) Sells(x, y, z) Hostile(z) Criminal(x) Nono … has some missiles, i. e. , x Owns(Nono, x) Missile(x): Owns(Nono, M 1) and Missile(M 1) … all of its missiles were sold to it by Colonel West Missile(x) Owns(Nono, x) Sells(West, x, Nono) Missiles are weapons: Missile(x) Weapon(x) An enemy of America counts as "hostile“: Enemy(x, America) Hostile(x) West, who is American … American(West) The country Nono, an enemy of America … Enemy(Nono, America)

Backward chaining example

Backward chaining example

Backward chaining example

Backward chaining example

Backward chaining example

Backward chaining example

Backward chaining example

Backward chaining example

Properties of backward chaining • Depth-first recursive proof search: space is linear in size of proof • Incomplete due to infinite loops – fix by checking current goal against every goal on stack • Inefficient due to repeated subgoals (both success and failure) – fix using caching of previous results (extra space) • Widely used for logic programming

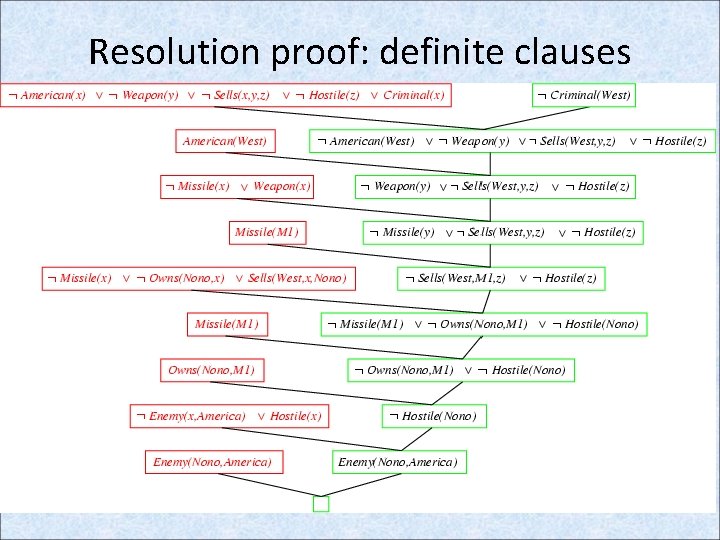
Resolution: brief summary • Full first-order version: l 1 ··· lk, m 1 ··· mn (l 1 ··· li-1 li+1 ··· lk m 1 ··· mj-1 mj+1 ··· mn) θ where Unify(li, mj) = θ for some i, j • The two clauses are assumed to be standardized apart so that they share no variables. For example, Rich(x) Unhappy(x) Rich(Ken) Unhappy(Ken) with θ = {x/Ken} • Apply resolution steps to CNF(KB α); complete for FOL

Resolution proof: definite clauses