CS 4100 Artificial Intelligence Prof C Hafner Class

CS 4100 Artificial Intelligence Prof. C. Hafner Class Notes Jan 19, 2012

Beliefs of the agent as a logical theory • A theory is a set of logical sentences (axioms) • We view this as a KB of the agent’s beliefs • The truth or falsity of other sentences may follow logically from the agent’s beliefs (is entailed) • For some sentences S, neither S nor ~S is entailed by the agent’s beliefs -- therefore in general a theory corresponds to many world models. • As a theory gets bigger (by adding sentences), its set of models gets smaller.

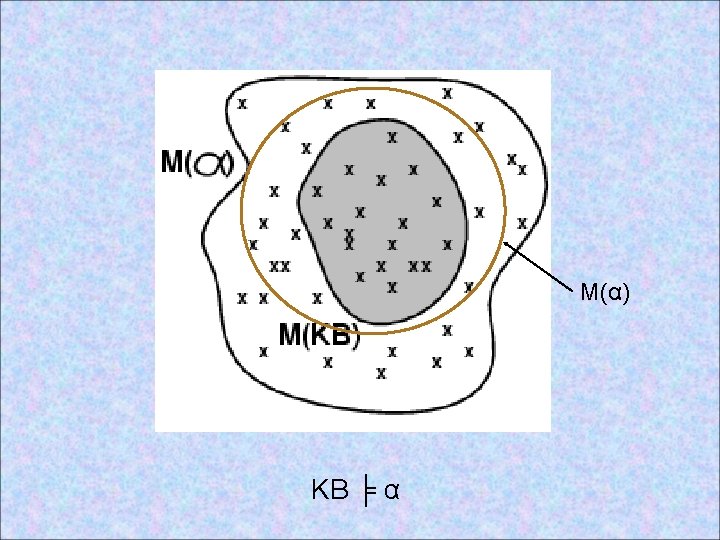
Models and Logical Entailment • Semantics for logic is truth-functional and is defined in terms of models, which are formally structured worlds with respect to which truth can be evaluated. If m is a model, then m assigns true or false to every logical sentence. • We say m is a model of a sentence α if α is true in m • M(α) is the set of all models of α • Then KB ╞ α iff M(KB) M(α) – E. g. KB = Giants won and Reds won – α = Giants won

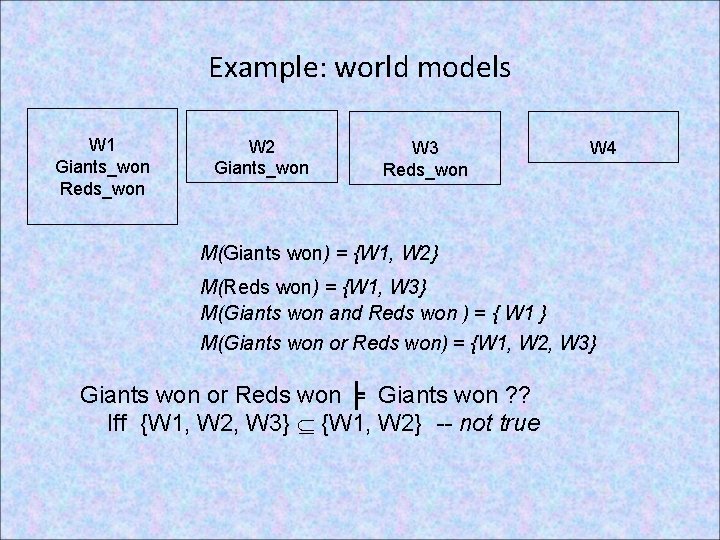
Example: semantics of logic: W 1 Giants_won Reds_won W 2 Giants_won W 3 Reds_won M(α) is the set of all models of α What are each of these: M(Giants won) M(Reds won) M(Giants won and Reds won ) M(Giants won or Reds won) W 4

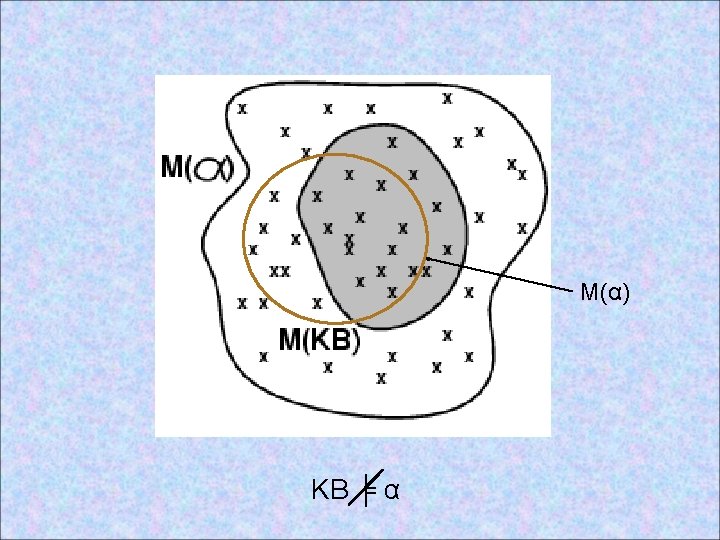
Example: world models W 1 Giants_won Reds_won W 2 Giants_won W 3 Reds_won W 4 M(Giants won) = {W 1, W 2} M(Reds won) = {W 1, W 3} M(Giants won and Reds won ) = { W 1 } M(Giants won or Reds won) = {W 1, W 2, W 3} Giants won or Reds won ╞ Giants won ? ? Iff {W 1, W 2, W 3} {W 1, W 2} -- not true

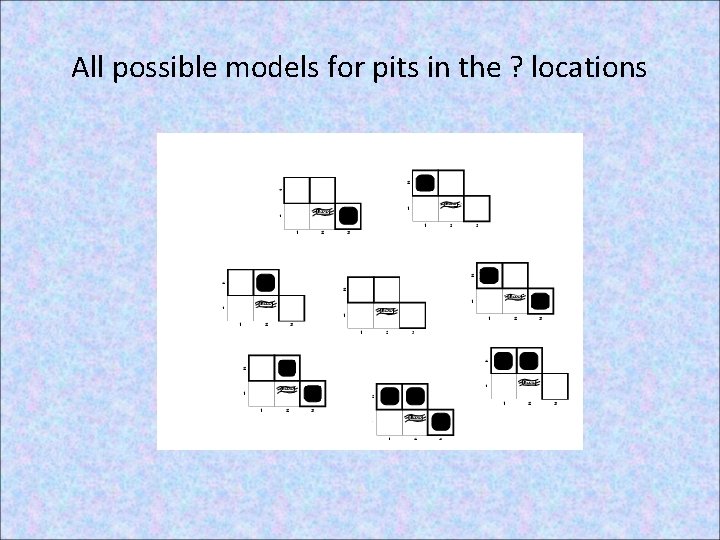
Computing entailment in the wumpus world Situation after detecting nothing in [1, 1], moving right, breeze in [2, 1] Consider possible models for the existence of pits in the 3 squares marked ? 3 Boolean choices 8 possible models

All possible models for pits in the ? locations

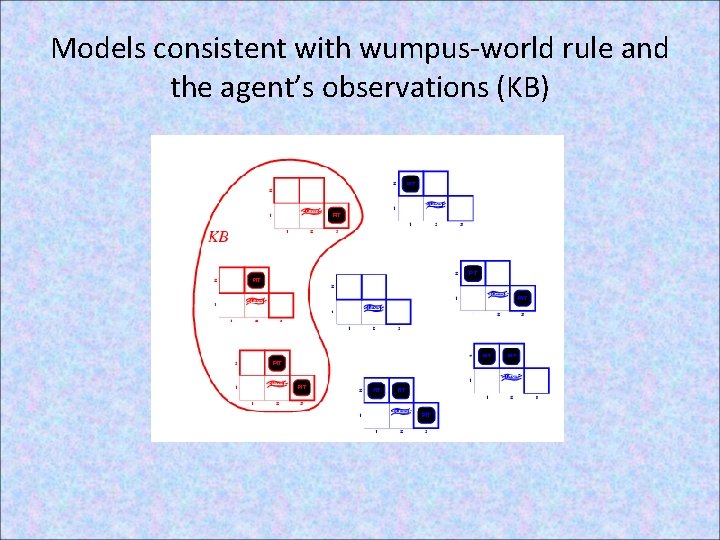
Models consistent with wumpus-world rule and the agent’s observations (KB)

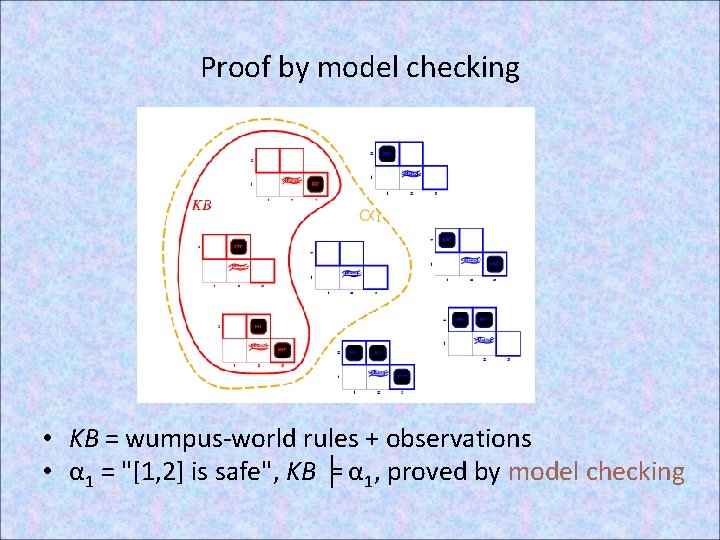
Proof by model checking • KB = wumpus-world rules + observations • α 1 = "[1, 2] is safe", KB ╞ α 1, proved by model checking

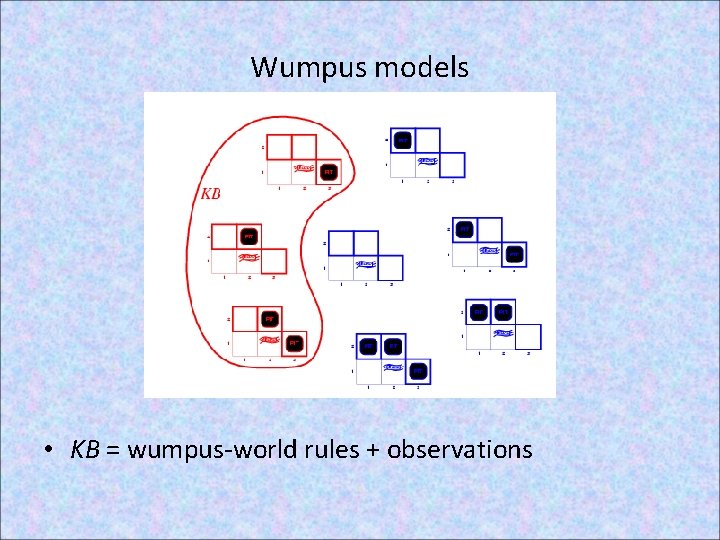
Wumpus models • KB = wumpus-world rules + observations

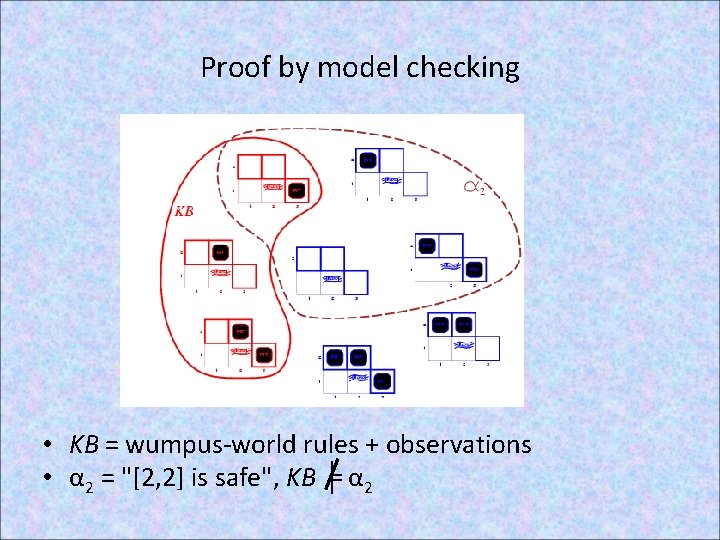
Proof by model checking • KB = wumpus-world rules + observations • α 2 = "[2, 2] is safe", KB ╞ α 2

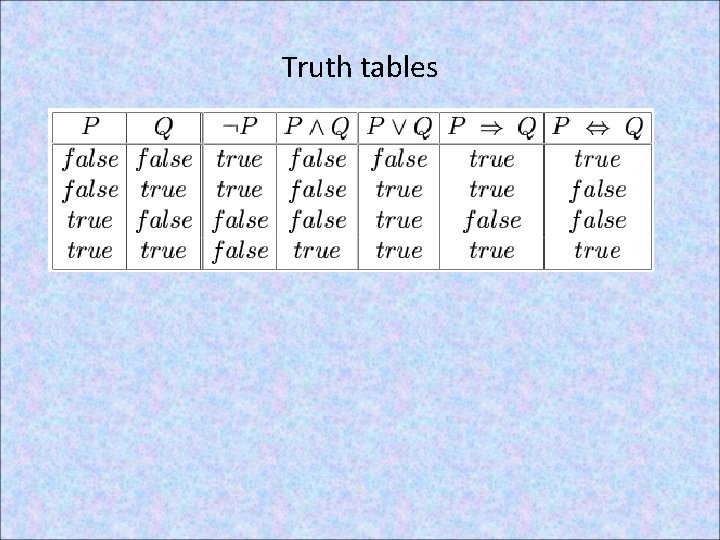
Truth tables

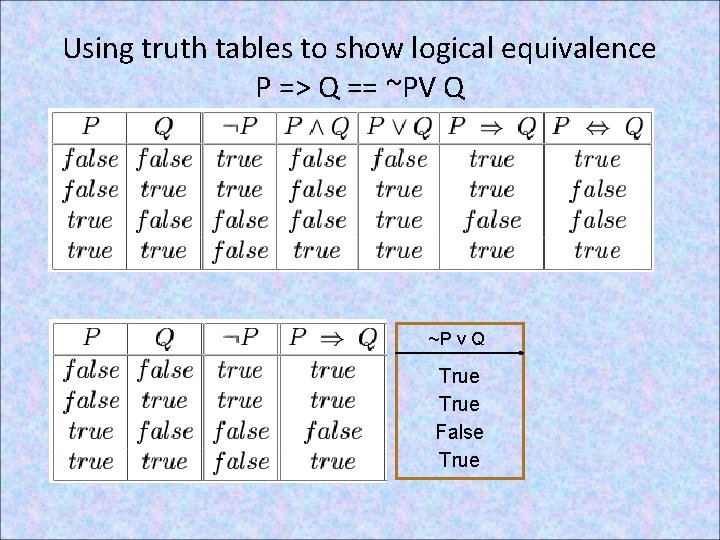
Using truth tables to show logical equivalence P => Q == ~PV Q ~P v Q True False True

Syntactic Reasoning: Sound rules of inference Name Premise(s) Derived Sentence Modus Ponens A, A => B B And Introduction A, B A^B And Elimination A^B A Double Negation ~~A A Unit Resolution A v B, ~B A Resolution A v B, ~B v C Av. C When we put the KB into clause form, then Resolution is both a complete and a sound rule of inference

The resolution rule Name Premise(s) Derived Sentence Resolution A v B, ~B v C A v C Show that modus ponens is a special case of the resolution rule: B B C (same as ~B v C) --------C

Representing Wumpus world w/ Propositional Logic (PL) Let Pi, j be true if there is a pit in [i, j]. (16 propositions) Let Bi, j be true if there is a breeze in [i, j]. P 1, 1 B 2, 1 • "Pits cause breezes in adjacent squares“ (“axioms”) B 1, 1 B 2, 1 (P 1, 2 P 2, 1) (P 1, 1 P 2, 2 P 3, 1) Note that in propositional logic, we can’t generalize the knowledge about breezes and adjacent squares. Why? ? No variables!! (a simplified answer)

Clauses and Inference • Def: a literal is an “atomic sentence”: P, Q, R Or the negation of an atomic sentence: P • Def: a clause is a disjunction of literals: Pv Qv. R • Def: a KB is in Conjunctive Normal Form (CNF) if it is represented as a conjunction of disjunctions of literals. In practice we use a set of clauses (conjunction is implicit) representing the agent’s beliefs • ---------------------------------- • Def: a Horn clause is a clause with at most one positive literal P 1 v P 2 v. . . Pn • A definite clause is a Horn clause with exactly one positive literal P 1 v P 2 v. . . Pn v R

Clauses and Inference • Theorem: any set of logic sentences can be transformed into CNF (conjunctive normal form) • Resolution – sound and complete inference method for KB in CNF – we only need that one inference rule !! • Two more efficient inference methods that work for Horn Clauses: – Forward chaining (data driven) – Backward chaining (goal driven)

The Resolution Inference Rule for Propositional Logic [P 1 v P 2 v. . . Pk ] [ P 1 v Q 2 v. . . Qn ] -------------------------P 2 v. . . Pk v Q 2 v. . . Qn

Applying Resolution to Clauses C 1. A v B v C v D v E v F C 2. P v Q v F v R v S -------------------These two clauses “RESOLVE”. The resolvent is: Av Bv Cv Pv Qv. Dv. Ev. Rv. S Note convention of ordering clauses: negative literals, then positive literals.

Implicative form for clauses Av Bv Cv Dv. E Note convention of ordering clauses: negative literals, then positive literals. Same as: A^B^C Dv. E (Proof of this is part of assignment 2)

Example Proof by Resolution Axioms: Qualified Hireable College-degree Experience Qualified Axioms: Qualified v Hireable College-degree v Experience v Qualified --------------------------- College-degree v Experience v Hireable Note: does this mean if a person is hireable they have a college degree and experience? Justify your answer.

Class Exercise (from text) • Given the following, can you prove that the unicorn is mythical? Magical? Horned? If the unicorn is mythical, then it is immortal, but if it is not mythical, then it is a mortal mammal. If the unicorn is either immortal or a mammal, then it is horned. The unicorn is magical if it is horned.

Forward Chaining Start with a percept derives new knowledge • Horn clauses: • C 1. P 1 v P 4 P 1 P 4 • C 2. P 4 v P 5 P 4 P 5 • ------------Step 1: Percept P 1 resolve with C 1 to get P 4 Step 2: Resolve P 4 with C 2 to get P 5 This is called Rule Chaining In practical Horn Clause reasoning: Q is called a “fact”, Q S is called a “rule” [from a formal logic standpoint, all sentences represent facts]

Backward Chaining • Horn clauses: • C 1. P 1 v P 2 v P 4 P 1 P 2 P 4 • C 2. P 4 v P 5 P 4 P 5 ------------ • Goal: prove: P 5 (Backward chaining) – Subgoal: prove P 4 – To prove P 4 • Sub-sub-goal: prove P 1 • Sub-sub-goal: prove P 2

Any KB (i. e. , any sentence) can be transformed into an equivalent CNF representation 1. 2. 3. 4. 5. Replace P => Q with P v Q Replace P with P Replace (P v Q) with P ^ Q Replace (P ^ Q) with P v Q Apply distributive rule replacing: (P ^ Q) v R with (P v R) ^ (Q v R)

Example P v Q => R ^ S (P v Q) v (R ^ S) ( P ^ Q) v (R ^ S) (( P ^ Q) v R ) ^ (( P ^ Q) v S) (1) (3) (5) Clause DB: Pv. R^ Qv. R^ Pv. S^ Qv. S (5, 5) Convert back to implicative form for intuition ? ?

Discussion of Assignments: Forward Chaining KB: agent’s beliefs(sometimes called “facts” and “rules”) fruit edible vegetable ^ green healthy apple fruit banana fruit spinach vegetable spinach green edible ^ healthy recommended ----------- New Percepts -------------- spinach

• Next time: – Discuss the backward chaining algorithm – Move on to FOL (first order logic) and extending our three inference methods to structured beliefs