CS 4026 Formal Models of Computation Part III

CS 4026 Formal Models of Computation Part III Computability & Complexity Part III-A – Computability Theory

Decidability Overview (Chapter 4 of Sipser’s Book) • Decidable languages • The Halting Problem Motivation – Investigate the power of algorithms to solve problems – Some problems can be solved, others cannot! – If you know a problem is algorithmically unsolvable then it must be simplified before we propose an algorithm • Instead of Hilbert’s problem, you might build an algorithm for deciding whether any roots exist between -n and +n. – Computers have limitations – we must consider these if we want to use computers well formal models of computation 2

Decidable Languages • Let’s look at problems concerning finite automata – We shall use “languages” to represent problems – We already have a terminology to deal with languages • In this area we present mere sketches of proofs • More precise proofs will re-appear when we turn to undecidable languages formal models of computation 3

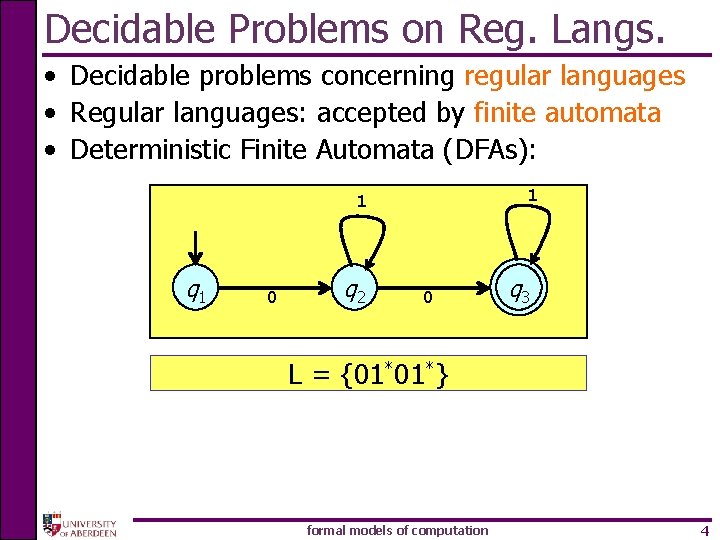
Decidable Problems on Reg. Langs. • Decidable problems concerning regular languages • Regular languages: accepted by finite automata • Deterministic Finite Automata (DFAs): 1 1 q 1 0 q 2 0 q 3 L = {01*01*} formal models of computation 4

Decidable Problems on R. L. (Cont’d) • The acceptance problem for DFAs: given – A deterministic finite automaton (DFA) and – A string check if the automaton accepts the string • Language contains the encodings of all DFAs coupled with strings that the DFAs accept: ADFA = { B, w | B is a DFA that accepts input string w } • “DFA B accepts input w ” same as “ B, w ADFA” – Other computational problems can be formulated in terms of testing membership of a set – Showing that the language is decidable is the same as showing the computational problem is decidable formal models of computation 5

Decidable Language 1 Theorem: “ADFA is a decidable language” Proof sketch: We only need to present a TM M that decides ADFA M = “On input B, w , where B is a DFA and w is a string: 1. Simulate B on input w 2. If the simulation ends in an accepting state of B , then accept; If the simulation ends in a non-accepting state of B, then reject. ” We don’t prove that simulation is possible. . . formal models of computation 6

. . . but note that the transitions of an DFA can be encoded as follows: • • • Each of the states qi is encoded as a string: q 1=DA, q 2=DAA, q 3=DAAA, . . . Each of the symbols Sj is encoded as a string: S 1=DC, S 2=DCC, S 3=DCCC, . . . Now each transition rule can be encoded as a string. E. g. d(q 1, S 2)=q 2 is endoded as DADCCDAAE (with E for “end of transition”) The algorithm terminates because the number of steps needed by a DFA to reach accept/reject is finite (bounded by the number of symbols in the string w). formal models of computation 7

Decidable Language 2 • Is there an algorithm to check if a DFA accepts any strings at all? • In terms of languages: EDFA = { A | A is a DFA and L (A) = } formal models of computation 8

Decidable Language 2 (Cont’d) Theorem: “EDFA is a decidable language” Proof: a DFA accepts some string if, and only if, it is possible to go from the start state to an accept state following the arrows A TM T that decides EDFA: T = “On input A , where A is a DFA: 1. Mark the start state of A 2. Repeat until no new states get marked: 3. Mark any state that has a transition coming into it from any marked state 4. If an accept state is marked, accept; otherwise reject” formal models of computation 9

Decidable Language 3 • Is there an algorithm to check if two DFAs are equivalent, i. e. , they recognise the same language? • In terms of languages: EQDFA = { A, B | A and B are DFAs and L (A) = L (B )} • In the true spirit of software reuse, let’s devise a solution to this problem using the previous MT! formal models of computation 10

Decidable Language 3 (Cont’d) • We build a new DFA C from A and B such that – C accepts only those strings that are accepted either by A or B but not both; – A and B recognise the same language iff C is empty • The language of C is L (C ) = (L (A ) L (B )) – This is the symmetric difference of L (A ) and L (B ) – L (A ) is the complement of L (A ) – Diagrammatically: in grey, L (C ) L (A ) L (B ) formal models of computation 11

Decidable Language 3 (Cont’d) • We build C from A and B with operations on DFAs: – – We We can can build a DFA that recognises L (A ) L (B ) build a DFA that recognises L (A ) therefore build a DFA that recognises C • For DFAs, there is no difference between recognizing and deciding • DFAs can be implemented using TMs – TMs can perform them! • Once we have built C, we can use previous TM to check if L (C ) is empty – if L (C ) is empty then L (A ) = L (B ) formal models of computation 12

Decidable Language 3 (Cont’d) The proof is an MT: F = “On input A, B where A and B are DFAs: 1. Build DFA C as described 2. Run TM T from previous example on C 4. If T accepts, accept; If T rejects, reject” Bringing together CS 3012 and CS 4026: formal models of computation 13

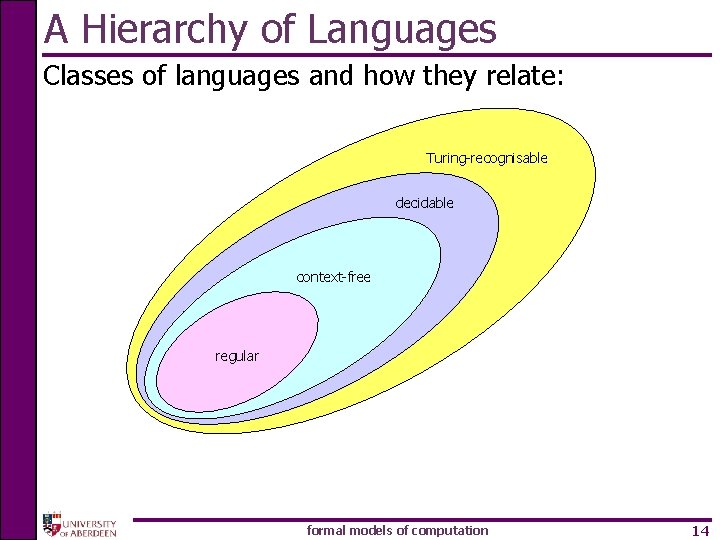
A Hierarchy of Languages Classes of languages and how they relate: Turing-recognisable decidable context-free regular formal models of computation 14

Before we get to the Halting Problem Prerequisites in set theory 1. The Russell Paradox. (See CS 3511, or any text book on set theory. ) 2. Classification of functions using the concepts of an injection, surjection, bijection/one-to-one correspondence (See CS 3511, or any text book on set theory) You may need to study these for yourself. Details are not repeated in these lectures. formal models of computation 15

The Diagonalisation Method • Proposed by Georg Cantor (1873) • Can we compare the size of infinite sets? – For finite sets this is straightforward: count! – But how about infinite sets? • Example: card(N ) > card({0*1*})? – Both are infinite – But is one larger than the other? • Cantor’s idea: – The size (cardinality) of a set should not depend on the identity of its elements – Two finite sets A and B have the same size if we can pair the elements of A with elements of B – We can extend the idea to infinite sets… formal models of computation 16

Correspondences • Assume sets A and B and function f from A to B • f is one-to-one (also: injective) if it does not map a, b A onto the same element in B , that is: if a b then f (a) f (b) • f is onto (also: surjective) if for every b B there is an a A such that f (a) = b • Functions that are both one-to-one and onto are (one-to-one) correspondences (Also: bijections) • Sets A and B have same size if we can show there is a correspondence between their elements: – Every element of A maps to a unique element of B – Each element of B has a unique elem. of A mapping to it Cantor’s definition of “same size” (“same cardinality”) formal models of computation 17

Correspondences (Cont’d) • Example: Let – N be the set of natural numbers {1, 2, 3, …} – E be the set of even natural numbers {2, 4, 6, …} • Intuitively, E is smaller than N ! • However, 1 2 3 2 4 6 … – Correspondence f (n) = 2 n – A table showing the pairing … • Using Cantor’s definition of size, we can show that N and E have the same size: n f ( n) – Pairing each element of N with its corresponding element in E is possible, – So we declare these two set to be the same size – This is even though E N (E is a real subset of N ) formal models of computation 18

Countable sets • We say: a set is countable if either – It is finite or – It has the same size as N, the natural numbers • For example, – – N is countable, and so are all its subsets: E is countable {0, 1, 2, 3} is countable • How about supersets of N? formal models of computation 19

An Even Stranger Example… • • Let Q be the set of positive rational numbers Q = { m/n | m, n N } Just like E, the set Q has the same size as N ! – We show this giving a correspondence from Q to N – Q is thus countable • One way to give a correspondence between a set X and N is to enumerate (i. e. , to list) X’s elements. For example, for X=Q : 1. List all the elements of Q 2. Pair the first element of the list with 1 from N 3. Pair the second element of the list with 2 from N And so on, making sure every member of Q appears only once in the list formal models of computation 20

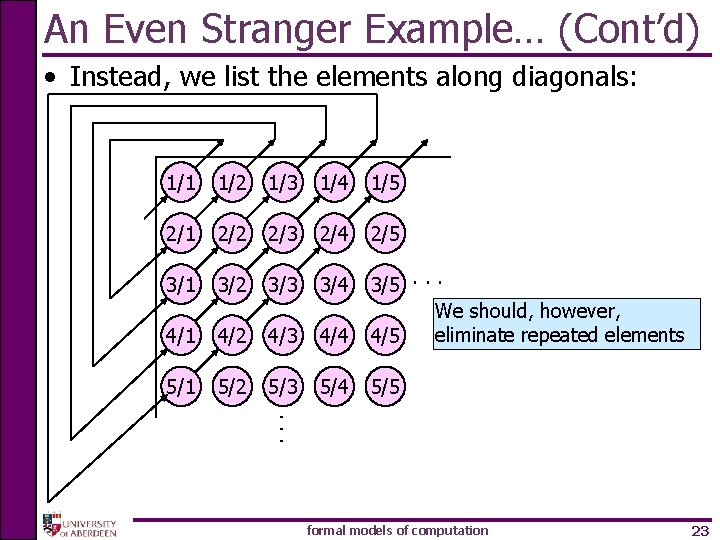
An Even Stranger Example… (Cont’d) • To build a list with the elements of Q – – make infinite matrix with all positive rational numbers i -th row contains all numbers with numerator i j -th column has all numbers with denominator j i /j is in i -th row and j -th column 1/1 1/2 1/3 1/4 1/5 2/1 2/2 2/3 2/4 2/5. . . 3/1 3/2 3/3 3/4 3/5 4/1 4/2 4/3 4/4 4/5 5/1 5/2 5/3 5/4 5/5 . . . formal models of computation 21

An Even Stranger Example… (Cont’d) • Now we turn the previous matrix into a list • A bad way: begin list with first row – Since rows are infinite, we will never get to 2 nd row! formal models of computation 22

An Even Stranger Example… (Cont’d) • Instead, we list the elements along diagonals: 1/2 1/3 1/4 1/5 2/1 2/2 2/3 2/4 2/5 3/1 3/2 3/3 3/4 4/1 4/2 4/3 4/4 3/5. . . We should, however, eliminate repeated elements 4/5 5/1 5/2 5/3 5/4 5/5 . . . 1/1 formal models of computation 23

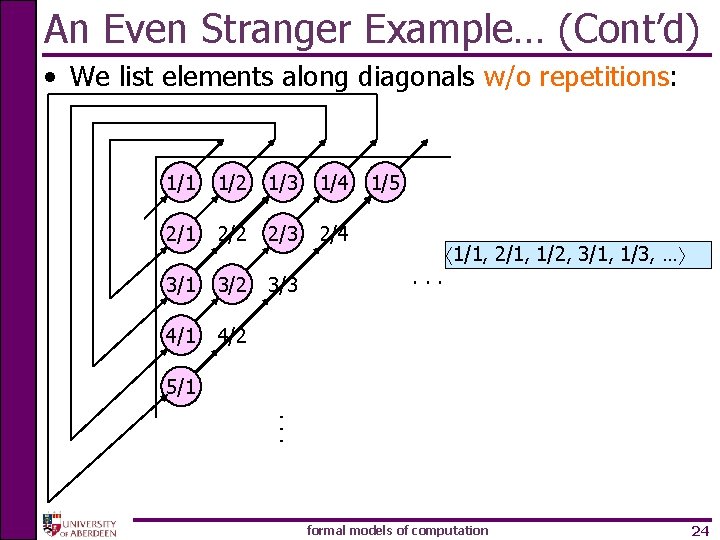
An Even Stranger Example… (Cont’d) • We list elements along diagonals w/o repetitions: 1/1 1/2 1/3 1/4 2/1 2/2 2/3 2/4 3/1 3/2 3/3 4/1 4/2 1/5 . . . 1/1, 2/1, 1/2, 3/1, 1/3, … . . . 5/1 formal models of computation 24

Uncountable sets • Some infinite sets have no correspondence with N • These sets are simply too big! – They are not countable: we say uncountable • Theorem: – The set of real numbers between 0 and 1 (e. g. , 0. 244, 0. 3141592323. . ) is uncountable Call this set R 0, 1 (Some sets are even larger. “Serious” set theory is all about calculations with infinite sets. – Most of this is irrelevant for this course. ) formal models of computation 25

Finally: diagonalisation Theorem: | R 0, 1 | > |N|. Proof strategy: | R 0, 1 |>=|N|. Suppose | R 0, 1 |=|N| and derive a contradiction: Each member of R 0, 1 can be written as a zero followed by a dot and a countable sequence of digits. Suppose there existed a complete enumeration of R, (using whatever order) <e 1, e 2, e 3, . . . >. For example, e 1. e 2. e 3. e 4. e 5. 0. 00000000000. . 0. 010000000000. . 0. 820000000000. . 0. 171000000000. . . . formal models of computation 26

Cantor’s diagonalisation trick: e 1. e 2. e 3. e 4. . 0. 00000000000. . 0. 010000000000. . 0. 820000000000. . 0. 1710000000000. . Now construct a Real number n not in the enumeration, as follows: n’s first digit (after the dot) = [e 1’s first digit] + 1 n’s second digit = [e 2’s second digit] + 1. . . General: n’s i-th difit = [e-i’s i-th digit] + 1 i: n differs from e-i in its i-th digit Contradiction: <e 1, e 2, e 3, . . . > is not a (complete) enumeration after all. QED formal models of computation 27

A corollary for computing • There are uncountably many languages/problems • There are countably many TMs Since – Each TM can only recognise a single language – There are more languages than TMs we can conclude that – Some languages are not recognised by any TM. That is: – Some languages are not Turing-recognisable Lets look at this argument in more detail formal models of computation 28

More Languages than TMs • First: There are countably many TMs. How Turing enumerated them (sketch): 1. Each of the countably many states qi is encoded as a string: q 1=DA, q 2=DAA, q 3=DAAA, . . . 2. Each of the symbols Sj is encoded as a string: S 1=DC, S 2=DCC, S 3=DCCC, . . . 3. Now each transition rule can be encoded as a string. E. g. d(q 1, S 2)=q 2, S 4, R is endoded as DADCCDAADCCCCRE (with E for “end of transition”) 4. Replace each letter by a digit: the result is a positive integer. 5. The TM is represented by stringing together these integers. Each integer represents at most one TM. formal models of computation 29

• The same argument shows that there are only countably many possible – – JAVA programs web pages novels. . . • Essentially, this is because each of these has a finite alphabeth and a finite (though unlimited!) length formal models of computation 30

More Languages than TMs • Second: There are uncountably many problems/languages This is most easily shown by focussing on a particular class of problems. For example, – Consider all functions f : : Int -> Int Each defines a language of 3 -tuples. For example (f 1, x, y) iff f 1(x)=y – The number of functions of this type is uncountable. Prove this using Cantor’s diagonal argument: Try to enumerate all functions fi; each fi(j) is defined for every integer j. Define a new function g as g(j)=fj+1. g cannot be an element of the enumeration. formal models of computation 31

Uncountably many f : : Int -> Int 1 2 3 4 5 6 7 8. . . f 1. f 2. f 3. f 4. . g differs from f 1 on the argument 1 g differs from f 2 on the argument 2. . . etc. So: g is not in the enumeration! formal models of computation 32

Where we are now • You’ve seen a very abstract proof that some languages are not Turing-decidable. – In laymen’s terms: some problems are not computable • More specifically, you’ve seen that some functions f : : Int cannot be programmed using a TM • But we haven’t shown you a concrete example (e. g. , a concrete problem for which there is no algorithm). • We now focus on one example: the halting problem formal models of computation 33

The Halting Problem • One of the most important theorems in CS theory – A specific problem algorithmically unsolvable – A proof that there isn’t an algorithm for a problem! • Computers are v. powerful – Will every problem be solved with Pentium XI? – No: computing is limited in a fundamental way • Is the following possible? Write a program to 1. read any program p plus any input i to p 2. decide if p terminates for i formal models of computation 34

The Halting problem Important for two reasons 1. One of the first problems to have been shown uncomputable; many other results in computability have been proven as a corollary 2. Halting is of intrinsic interest: Just like we want to know if a given program can sometimes come up with the wrong answer, we want to know if a program can sometimes come up with no answer • recall: the difference between recognising and deciding a language We focus on a slightly different problem first: the problem whether a given TM accepts a given string. (which implies that the TM halts on this string) formal models of computation 35

The Halting Problem (Cont’d) • Using our terminology and notation: ATM = { M, w | M is a TM that accepts input string w } • “M accepts w ” “ M, w ATM” • Theorem: ATM is undecidable – some introductory remarks before proving this • ATM is Turing-recognisable: U = “On input M, w where M is a TM and w is a string: 1. Simulate M on input w 2. If M enters its accept state, accept; If M enters its reject state, reject” • ATM is known as the Acceptance problem formal models of computation 36

Universal Turing Machine • TM U is important in its own right • An example of the universal TM – Able to simulate any other TM (given its description) • The first stored-program computer – For each new regular language, devise a DFA – For each new context-free language, devise a PDA – One TM is enough for all Turing-decidable/recognisable languages (we must propose a representation, though) – Compare: No need to assemble a PC differently for each Java program we need to run! • The universal TM simulates another TM using the same coding that we used when proving the set of TMs to be countable. [Details skipped here. ] formal models of computation 37

The Halting Problem (Cont’d) • TM U loops on M, w if M loops on w ! – That’s why it is not a decider – If U could check M wasn’t halting on w it could reject! • Idea: add a check “if M loops on w ” U = “On input M, w where M is a TM and w is a string: 1. Simulate M on input w 2. If M enters its accept state, accept; If M enters its reject state, reject; If M loops, reject” There is no algorithm to check this… There is no TM to perform this check… formal models of computation 38

ATM is undecidable • Let’s now prove the undecidability of ATM = { M, w | M is a TM that accepts input string w } • Proof by contradiction: – Assume ATM is decidable and obtain a contradiction • Decidability would mean there exists a decider H for ATM H ( M, w ) = accept if M accepts w reject if M does not accept w formal models of computation 39

ATM is undecidable (Cont’d) • We now build a new TM D with H as a “subroutine” – Informally speaking, D says: M does not accept M D( M )= not H M, M – A description of D is D = “On input M where M is a TM: 1. Run H on input M, M 2. Output the opposite of what H outputs; that is if H accepts, reject and if H rejects, accept. ” D is like the barber who cuts the hair of exactly those people who do not cut their own hair! • This is like running a program with itself as an input • For instance, a Java compiler written in Java… formal models of computation 40

Halt. Probl. is undecidable (Cont’d) • In summary D ( M ) = accept if M does not accept M reject if M accepts M • What happens if we run D with its own description D as input? In this case we shall get: D ( D ) = accept if D does not accept D reject if D accepts D • No matter what D does, it must also do the opposite – this is a contradiction! – Neither TM D nor TM H can exist formal models of computation 41

Halt. Probl. is undecidable (Cont’d) • The steps of the proof are: – Assume that a TM H decides ATM – Use H to build a TM D which accepts M iff M does not accept input M – Finally, run D on itself • The machine takes the following actions: – H accepts M, w iff M accepts w – D accepts M iff M rejects M – D accepts D iff D rejects D Contradiction!! formal models of computation 42

A Turing-Unrecognisable Language • Definition: A language is co-Turing-recognisable iff it is the complement of a Turing-recognisable language • Theorem: – A language is decidable if and only if it is both Turingrecognisable and co-Turing-recognisable • The complement of ATM is not Turing-recognisable – ATM is Turing-recognisable – If the complement of ATM were also Turing-recognisable, ATM would be decidable formal models of computation 43

Reading List • Introduction to the Theory of Computation. Michael Sipser. PWS Publishing Co. , USA, 1997. (A 2 nd Edition has recently been published). Chapter 4. • Algorithmics: The Spirit of Computing. 3 rd Edition. David Harel with Yishai Feldman. Addison-Wesley, USA, 2004. Chapter 8. formal models of computation 44