CS 361 Chapter 11 Divide and Conquer Examples

CS 361 – Chapter 11 • Divide and Conquer ! • Examples: – – Merge sort √ Ranking inversions Matrix multiplication Closest pair of points • Master theorem – A shortcut way of solving many, but not all, recurrences.

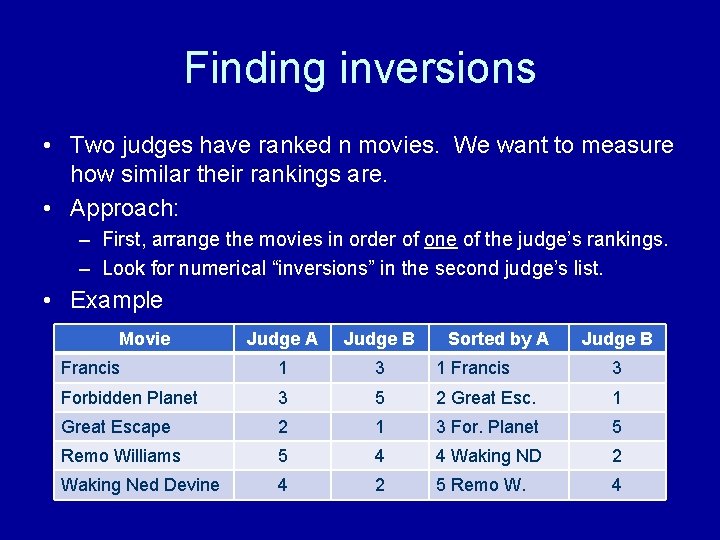
Finding inversions • Two judges have ranked n movies. We want to measure how similar their rankings are. • Approach: – First, arrange the movies in order of one of the judge’s rankings. – Look for numerical “inversions” in the second judge’s list. • Example Movie Judge A Judge B Sorted by A Judge B Francis 1 3 1 Francis 3 Forbidden Planet 3 5 2 Great Esc. 1 Great Escape 2 1 3 For. Planet 5 Remo Williams 5 4 4 Waking ND 2 Waking Ned Devine 4 2 5 Remo W. 4

How to do it • We’re given (3, 1, 5, 2, 4). Compare with (1, 2, 3, 4, 5). • One obvious solution is O(n 2). Look at all possible pairs of rankings and count those that are out of order. – For each # in list, see if subsequent values are smaller. This would be an inversion. – 3 > 1, 2 – 1 > [nothing] – 5 > 2, 4 – 2 > [nothing] – 4 > [nothing] – The answer is 4 inversions. • But we can devise an O(n log 2 n) solution that operates like merge sort!

Algorithm • Split up the list in halves until you have singleton sets. • Our merge procedure will – Take as input 2 sorted lists, along with the number of inversions that appeared in each – Return a (sorted) merged list and the number of inversions • Singleton set has no inversions. Return 0. • How to combine: – – – Let i point to front/smallest value in A. Let j point to front/smallest value in B. Which is smaller, A[i] or B[j]? Remove smaller to C. If it came from B, increment count by |A|. When one list empty, you are essentially done. Return # of inversions = count + A. count + B. count

Example • Count inversions in: 5, 4, 7, 3, 2, 6, 1, 8 • Along the way, we find that: – – – (5, 4) has 1 inversion (7, 3) has 1 inversion ((4, 5), (3, 7)) has 2 additional inversions, subtotal 1+1+2 = 4 ((2, 6), (1, 8)) has 2 additional inversions, subtotal 0+0+2 = 2 ((3, 4, 5, 7), (1, 2, 6, 8)) has 9 additional inversions, bringing our total to 4 + 2 + 9 = 15. • We can verify that there are in fact 15 inversions. • Interesting that we have an O(n log 2 n) algorithm to find inversions, even though our answer can be as high as C(n, 2) which is O(n 2). Sorting helped!

Matrix operations • Many numerical problems in science & engineering involve manipulating values in a 2 -d arrays called matrices. • Let’s assume dimensions are n x n. • Adding and subtracting matrices is simple: just add corresponding values. O(n 2). • Multiplication is more complicated. Here is example: A B C=AB 1 3 8 6 1*8 + 3*2 1*6+3*7 4 5 2 7 4*8 + 5*2 4*6 + 5*7 • C[1, 2] = A[1, 1]*B[1, 2] + A[1, 2]*B[2, 2], etc. • C[i, j] = sum from k=1 to n of A[i, k]*B[k, j]

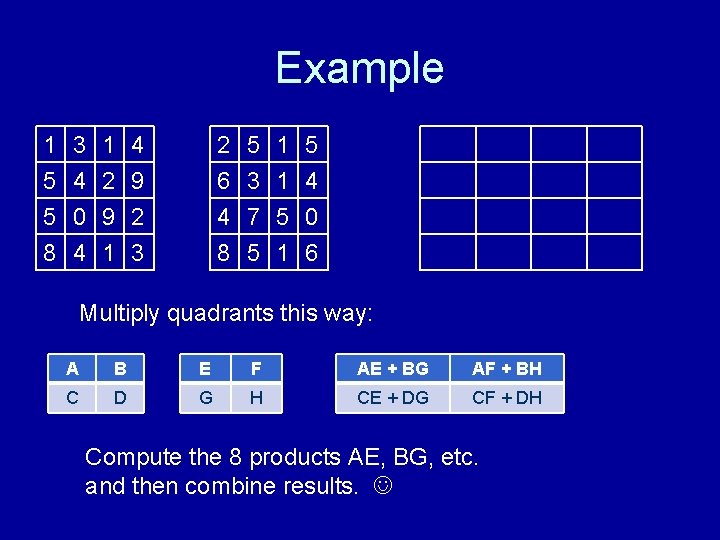
Multiplication • Matrix multiplication can thus be done in O(n 3) time, compared to O(n 2) for addition and subtraction. • Actually, we are overstating the complexity, because usually “n” is size of input. The complexities of n 2 and n 3 here assume we have n 2 of input. – But in the realm of linear algebra, “n” means how many rows/columns of data. • How can we devise a divide-and-conquer algorithm for matrix multiplication? – Partition the matrices into 4 quadrants each. – Multiply each quadrant independently.

Example 1 5 5 8 3 4 0 4 1 2 9 1 4 9 2 3 2 6 4 8 5 3 7 5 1 1 5 4 0 6 Multiply quadrants this way: A B E F AE + BG AF + BH C D G H CE + DG CF + DH Compute the 8 products AE, BG, etc. and then combine results.

Complexity • The divide-and-conquer approach for matrix multiplication gives us: T(n) = 8 T(n/2) + O(n 2). • This works out to a total of O(n 3). – No better than classic definition of matrix multiplication. – But, very useful in parallel computation! • Strassen’s algorithm: By doing some messy matrix algebra, it’s possible to compute the n*n product with only 7 quadrant multiplications instead of 8. – T(n) = 7 T(n/2) + O(n 2) implies T(n) O(n log 2 7). • Further optimizations exist. Conjecture: matrix multiplication is only slightly over O(n 2).

Closest pair • A divide-and-conquer problem. • Given a list of (x, y) points, find which 2 points are closest to each other. • (First, think about how you’d do it in 1 dimension. ) • Divide & conquer: repeatedly divide the points into left and right halves. Once you only have a set of 2 or 3 points, finding the closest is easy. • Convenient to have list of points sorted by x & by y. • Combine is a little tricky because it’s possible that the closest pair may straddle the dividing line between left and right halves.

Combining solutions • Given a list of points P, we divided this into a “left” half Q and a right half R. • Thru divide and conquer we now know the closest pair in Q [q 1, q 2] and closest pair in R [r 1, r 2], and we can determine which is better. • Let = min(dist(q 1, q 2), dist(r 1, r 2)) • But, there might be a pair of points [q, r] with q Q and r R whose dist(q, r) < . How would we find this mysterious pair of points? – These 2 points must be within distance of the vertical line passing thru the rightmost point in Q. Do you see why?

Boundary case • Let’s call S the list of points within horizontal (i. e. “x”) distance of the dividing line L. In effect, a thin vertical strip of territory. • We can restate our earlier observation as follows: There are two points q Q and r R with dist(q, r) < there are two points s 1, s 2 S with dist(s 1, s 2) < . • We can restrict our search for the boundary case even more. – If we sort S by y-coordinate, then s 1, s 2 are within 15 positions of each other on the list. – This means that searching for the 2 closest points in S can be done in O(n) time, even though it’s a nested loop. One loop is bounded by 15 iterations.

Why 15? • Take a closer look at the boundary region. • Let Z be the portion of the plane within x-distance from L. Partition Z into squares of side length /2. We will have many rows of squares, with 4 squares per row. • Each square contains at most 1 point from S. Why? – Suppose one square contains 2 points from S. Both are either in Q or in R, so their distance is at least . But the diagonal of the square is not this long. Contradiction. • s 1 and s 2 are within 15 positions in S sorted by y. Why? – Suppose separated by 16 or more. Then, there have to be at least 3 rows of squares separating them, so their distance apart must be at least 3 /2. However, we had chosen s 1 and s 2 because their distance was < . Contradiction.

Algorithm closest. Pair(list of points P): px and py are P sorted by x and y respectively if |px| <= 3, return the simple base case solution Create Q and R: the left & right halves of P. closest. Q = closest. Pair(Q) closest. R = closest. Pair(R) delta = min(dist(closest. Q), dist(closest. R)) S = points in P within delta of rightmost Q sy = S sorted by y for each s in sy: find dist from s to each of next 15 in sy let [s, s’] be this shortest pair in sy return closest of: closest. Q, closest. R, or [s, s’]

Master theorem • What is the complexity of an algorithm if we have this type of recurrence: T(n) = a T(n / b) + f(n) • For example, splitting a problem into “a” instances of the problem, each with size 1/b of the original. • 3 cases, basically comparing n log b a with f(n) to see which is “larger”: Condition on f(n) Form of T(n) O (n log b a – ε) n log b a Θ (n log b a ) n log b a log 2 n W (n log b a + ε) and c < 1, n 0 > 1, n>n 0: a f(n/b) c f(n)

How to use • • If we are given T(n) = a T(n / b) + f(n) Compare n log b a with f(n) Case 1: If n log b a is larger, then T(n) = O(n log b a ). Case 2: If equal, then T(n) = O(f(n) log 2 n). Incidentally, if f(n) is exactly (log 2 n)k times n log b a T(n) = O(f(n) (log 2 n)k+1). • Case 3: If f(n) is larger, then T(n) = O(f(n)). But need to verify that a f(n/b) < f(n) or else master theorem can’t guarantee answer.

Examples 1. T(n) = 9 T(n/3) + n 2. T(n) = T((2/3) n) + 1 3. T(n) = 3 T(n/4) + n log 2 n 4. T(n) = 4 T(n/2) + n 5. T(n) = 4 T(n/2) + n 2 6. T(n) = 4 T(n/2) + n 3 7. T(n) = 2 T(n/2) + n 3 8. T(n) = T(9 n/10) + n 9. T(n) = 16 T(n/4) + n 2 10. T(n) = 7 T(n/3) + n 2 11. T(n) = 7 T(n/2) + n 2 12. T(n) = 2 T(n/4) + n 0. 5 13. T(n) = 3 T(n/2) + n log 2 n 14. T(n) = 2 T(n/2) + n/ log 2 n 15. T(n) = 2 T(n/2) + n log 2 n 16. T(n) = 8 T(n/2) + n 3(log 2 n)5

Var substitution • Sometimes the recurrence is not expressed as a fraction of n. (See bottom of page 311. ) • Example: T(n) = T(n 0. 5) + 1 • Let x = log 2 n. This means that n = 2 x and n 0. 5 = 2 x/2 • T(n) formula becomes T(2 x) = T(2 x/2) + 1 • If you don’t like powers of 2 inside T, temporarily define similar function S(x) = T(2 x). • Now it is: S(x) = S(x/2) + 1. We know how to solve it. • S(x) = O(log 2 x). • Thus, T(2 x) = O(log 2 x). Replace x with log 2 n. • Final answer: T(n) = O(log 2 n)).