CS 344 Introduction to Artificial Intelligence Pushpak Bhattacharyya

CS 344 : Introduction to Artificial Intelligence Pushpak Bhattacharyya CSE Dept. , IIT Bombay Lecture 22 - Forward probability and Robot Plan

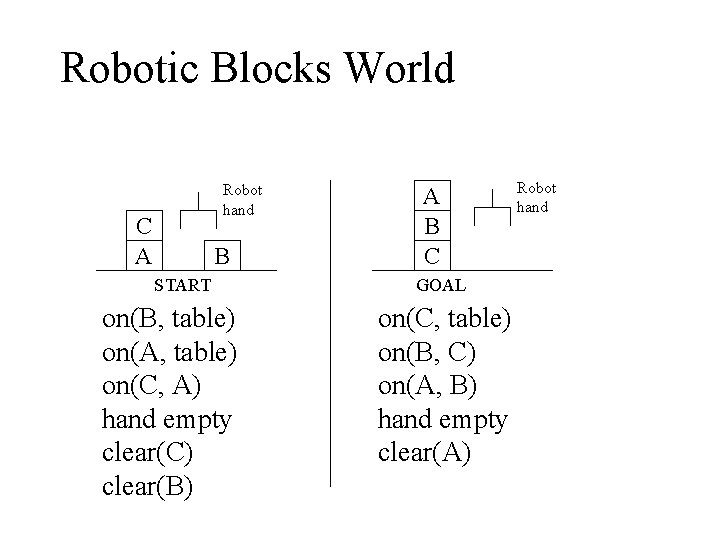
Robotic Blocks World Robot hand C A B START on(B, table) on(A, table) on(C, A) hand empty clear(C) clear(B) A B C GOAL on(C, table) on(B, C) on(A, B) hand empty clear(A) Robot hand

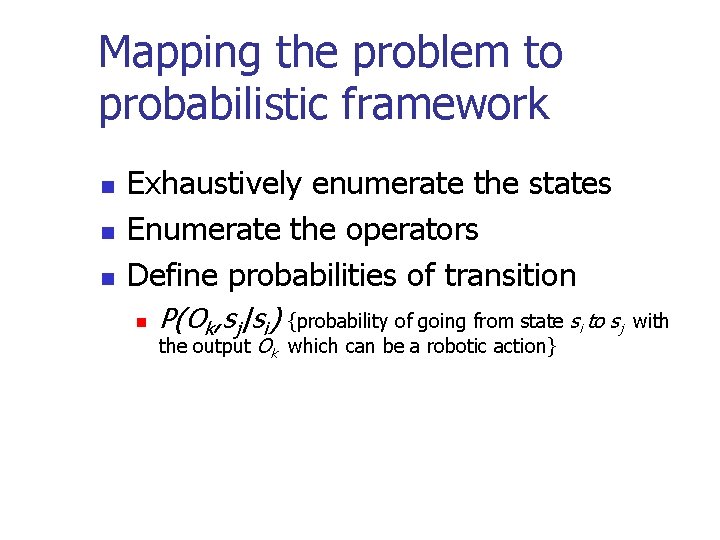
Mapping the problem to probabilistic framework n n n Exhaustively enumerate the states Enumerate the operators Define probabilities of transition n P(Ok, sj|si) {probability of going from state si to sj the output Ok which can be a robotic action} with

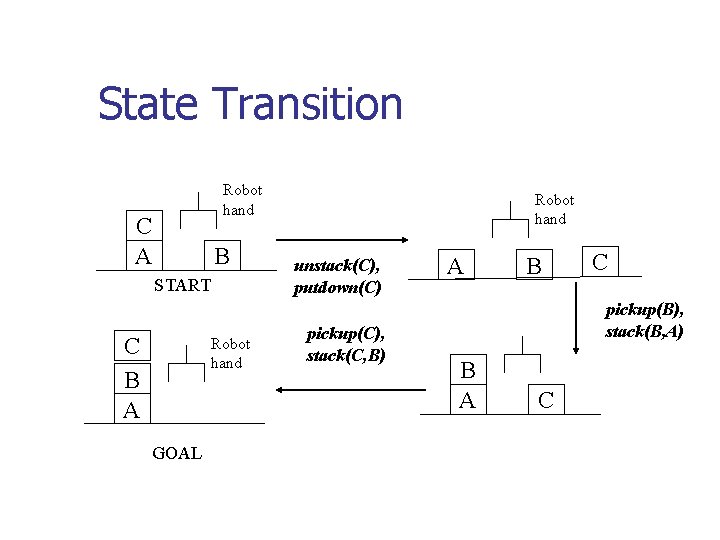
State Transition Robot hand C A B START C B A Robot hand GOAL Robot hand unstack(C), putdown(C) pickup(C), stack(C, B) A B C pickup(B), stack(B, A) B A C

States for Blocks world problem n Total 22 states • Hand – empty n No column (1 state) n 2 -blk-column (6 states) n 3 -blk-column (6 states) • Hand – holding n Block A in Hand – no column (1 state), 2 -blk-column (2 states) n Block B in Hand – no column (1 state), 2 -blk-column(2 states) n Block C in Hand – no column (1 state), 2 -blk-column(2 states)

State space and operators n n State space = {s 1, s 2, … , s 22} Operators • • pick up A (PA), pick up A (PB), pick up A (PC) put down(DA), put down(DB), put down(DC) stack(x , y) – total 6 operators i. e. TAB, TCB, TBC, TCA, TAC unstack (x) – UA, UB, UC

Probabilistic Automaton n n This gives a probabilistic automaton where probability values are specified between every states for each operator. We need to learn total 22 C 2 (states) * 15 (operators) different probability values, e. g. , P(PA, s 2 | s 1) = 0. 3, P(DC, s 5| s 2), …

Formula for Operator Sequence Probability n Forward Algorithm to calculate operator sequence probability. e. g. seq = UC DC PB TBA PC TCB P(seq) = P(UC DC PB TBA PC TCB ) = ∑ P(UC DC PB TBA PC TCB, s 6 = si) 21 i=0 (marginalization, probability of seq with 6 th state = si )

Back to HMM

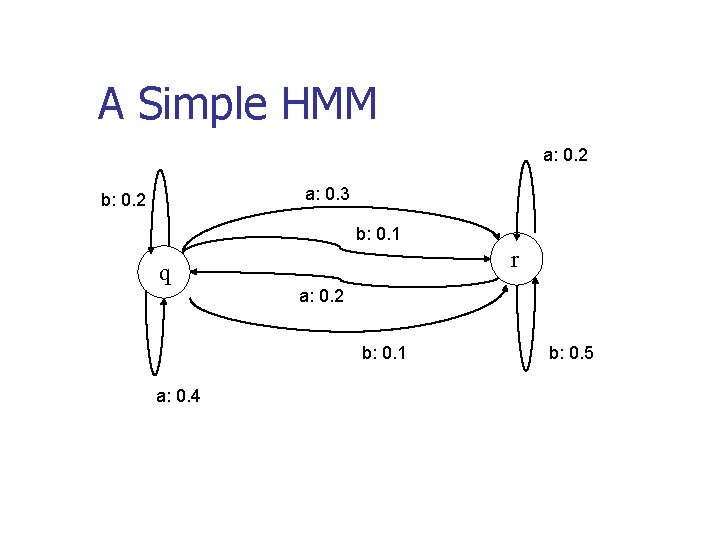
A Simple HMM a: 0. 2 a: 0. 3 b: 0. 2 b: 0. 1 r q a: 0. 2 b: 0. 1 a: 0. 4 b: 0. 5

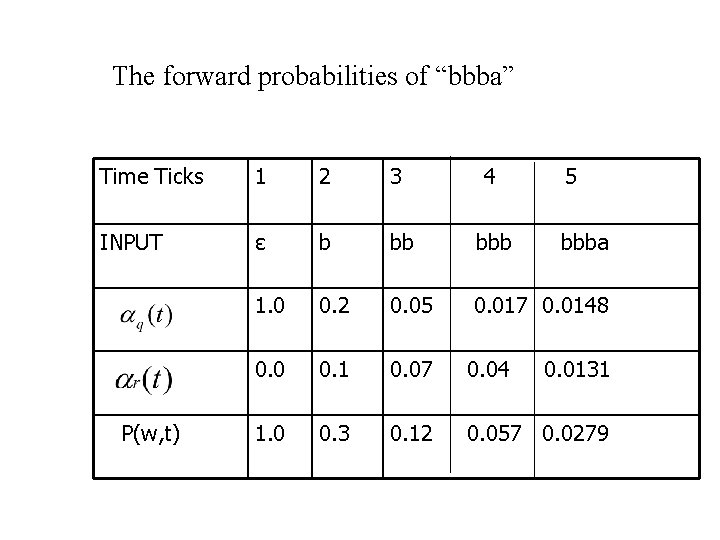
The forward probabilities of “bbba” Time Ticks 1 2 3 4 INPUT ε b bb bbb 1. 0 0. 2 0. 05 0. 017 0. 0148 0. 0 0. 1 0. 07 0. 04 1. 0 0. 3 0. 12 0. 057 0. 0279 P(w, t) 5 bbba 0. 0131