CS 3343 Analysis of Algorithms Lecture 9 Review















![Best case Inner loop stops when A[i] <= key, or i = 0 i Best case Inner loop stops when A[i] <= key, or i = 0 i](https://slidetodoc.com/presentation_image_h2/a5861d745be0a032aca3b74587c18312/image-16.jpg)
![Worst case Inner loop stops when A[i] <= key i j 1 sorted • Worst case Inner loop stops when A[i] <= key i j 1 sorted •](https://slidetodoc.com/presentation_image_h2/a5861d745be0a032aca3b74587c18312/image-17.jpg)
![Average case Inner loop stops when A[i] <= key i j 1 sorted • Average case Inner loop stops when A[i] <= key i j 1 sorted •](https://slidetodoc.com/presentation_image_h2/a5861d745be0a032aca3b74587c18312/image-18.jpg)

![Analyzing merge sort T(n) MERGE-SORT A[1. . n] Θ(1) 1. If n = 1, Analyzing merge sort T(n) MERGE-SORT A[1. . n] Θ(1) 1. If n = 1,](https://slidetodoc.com/presentation_image_h2/a5861d745be0a032aca3b74587c18312/image-20.jpg)
![Recursive Insertion Sort Recursive. Insertion. Sort(A[1. . n]) 1. if (n == 1) do Recursive Insertion Sort Recursive. Insertion. Sort(A[1. . n]) 1. if (n == 1) do](https://slidetodoc.com/presentation_image_h2/a5861d745be0a032aca3b74587c18312/image-21.jpg)
![Binary Search Binary. Search (A[1. . N], value) { if (N == 0) return Binary Search Binary. Search (A[1. . N], value) { if (N == 0) return](https://slidetodoc.com/presentation_image_h2/a5861d745be0a032aca3b74587c18312/image-22.jpg)









![Partition Code Partition(A, p, r) x = A[p]; // pivot is the first element Partition Code Partition(A, p, r) x = A[p]; // pivot is the first element](https://slidetodoc.com/presentation_image_h2/a5861d745be0a032aca3b74587c18312/image-36.jpg)















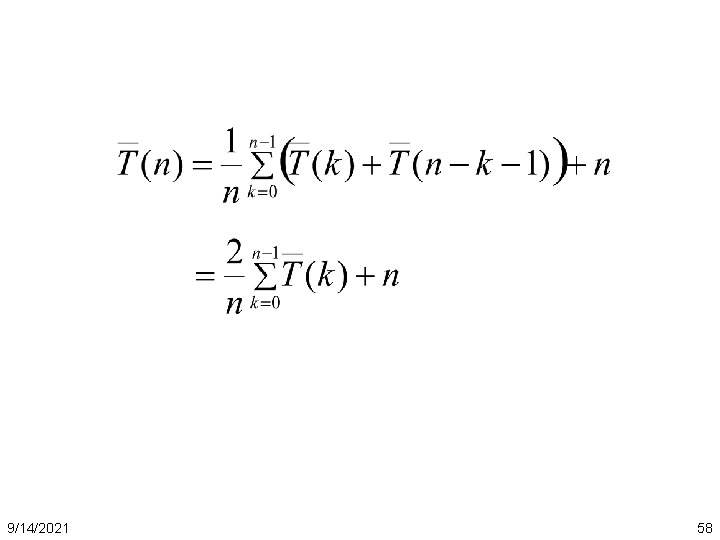









- Slides: 67

CS 3343: Analysis of Algorithms Lecture 9: Review for midterm 1 Analysis of quick sort 9/14/2021 1

Exam (midterm 1) • Closed book exam • One cheat sheet allowed (limit to a single page of letter-size paper, double-sided) • Tuesday, Feb 24, 10: 00 – 11: 25 pm • Basic calculator (no graphing) is allowed 9/14/2021 2

Materials covered • Up to Lecture 8 (Feb 6) • Comparing functions • O, Θ, Ω – Definition, limit method, L’Hopital’s rule, sterling’s formula • Analyzing iterative algorithms – Know how to count the number of basic operations, and express the running time as a sum of a series – Know how to compute the sum of a series (geometric, arithmetic, or other frequently seen series) • Analyzing recursive algorithms – – 9/14/2021 Define recurrence Solve recurrence using recursion tree / iteration method Solve recurrence using master method Prove using substitution method 3

Asymptotic notations • • • O: <= o: < Ω: >= ω: > Θ: = (in terms of growth rate) 9/14/2021 4

Mathematical definitions • O(g(n)) = {f(n): positive constants c and n 0 such that 0 ≤ f(n) ≤ cg(n) n>n 0} • Ω(g(n)) = {f(n): positive constants c and n 0 such that 0 ≤ cg(n) ≤ f(n) n>n 0} • Θ(g(n)) = {f(n): positive constants c 1, c 2, and n 0 such that 0 c 1 g(n) f(n) c 2 g(n) n n 0} 9/14/2021 5

Big-Oh • Claim: f(n) = 3 n 2 + 10 n + 5 O(n 2) • Proof by definition: f(n) = 3 n 2 + 10 n + 5 3 n 2 + 10 n 2 + 5 , n > 1 3 n 2 + 10 n 2 + 5 n 2, n > 1 18 n 2, n > 1 If we let c = 18 and n 0 = 1, we have f(n) c n 2, n > n 0. Therefore by definition, f(n) = O(n 2). 9/14/2021 6

Use limits to compare orders of growth f(n) o(g(n)) • lim f(n) / g(n) = n→∞ 0 c >0 ∞ f(n) O(g(n)) f(n) Θ (g(n)) f(n) Ω(g(n)) f(n) ω (g(n)) L’ Hopital’s rule lim f(n) / g(n) = lim f(n)’ / g(n)’ n→∞ Condition: If both lim f(n) and lim g(n) = ∞ or 0 Stirling’s formula (constant) 9/14/2021 7

Useful rules for logarithms For all a > 0, b > 0, c > 0, the following rules hold • logba = logca / logcb = lg a / lg b – So: log 10 n = log 2 n / log 2 10 • logban = n logba – So: log 3 n = n log 3 = (n) • b logba = a – So: 2 log 2 n = n • log (ab) = log a + log b – So: log (3 n) = log 3 + log n = (log n) • log (a/b) = log (a) – log(b) – So: log (n/2) = log n – log 2 = (log n) • logba = 1 / logab • logb 1 = 0 9/14/2021 8

Useful rules for exponentials • • • For all a > 0, b > 0, c > 0, the following rules hold a 0 = 1 (00 = ? ) Answer: does not exist a 1 = a a-1 = 1/a (am)n = amn (am)n = (an)m – So: (3 n)2 = 32 n = (32)n =9 n • aman = am+n – So: n 2 n 3 = n 5 – 2 n 22 = 2 n+2 = 4 * 2 n = (2 n) 9/14/2021 9

More advanced dominance ranking 9/14/2021 10

Sum of arithmetic series If a 1, a 2, …, an is an arithmetic series, then 9/14/2021 11

Sum of geometric series if r < 1 if r > 1 if r = 1 9/14/2021 12

Sum manipulation rules Example: 9/14/2021 13

Analyzing non-recursive algorithms • Decide parameter (input size) • Identify most executed line (basic operation) • worst-case = average-case? • T(n) = i ti • T(n) = Θ (f(n)) 9/14/2021 14

Analysis of insertion Sort Statement Insertion. Sort(A, n) { for j = 2 to n { key = A[j] i = j - 1; while (i > 0) and (A[i] > key) { A[i+1] = A[i] i = i - 1 } A[i+1] = key } } 9/14/2021 cost time__ c 1 c 2 c 3 c 4 c 5 c 6 0 c 7 0 n (n-1) S (S-(n-1)) (n-1) 15
![Best case Inner loop stops when Ai key or i 0 i Best case Inner loop stops when A[i] <= key, or i = 0 i](https://slidetodoc.com/presentation_image_h2/a5861d745be0a032aca3b74587c18312/image-16.jpg)
Best case Inner loop stops when A[i] <= key, or i = 0 i j 1 sorted • • 9/14/2021 Key Array already sorted S = j=1. . n tj tj = 1 for all j S = n. T(n) = Θ (n) 16
![Worst case Inner loop stops when Ai key i j 1 sorted Worst case Inner loop stops when A[i] <= key i j 1 sorted •](https://slidetodoc.com/presentation_image_h2/a5861d745be0a032aca3b74587c18312/image-17.jpg)
Worst case Inner loop stops when A[i] <= key i j 1 sorted • • 9/14/2021 Key Array originally in reverse order sorted S = j=1. . n tj tj = j S = j=1. . n j = 1 + 2 + 3 + … + n = n (n+1) / 2 = Θ (n 2) 17
![Average case Inner loop stops when Ai key i j 1 sorted Average case Inner loop stops when A[i] <= key i j 1 sorted •](https://slidetodoc.com/presentation_image_h2/a5861d745be0a032aca3b74587c18312/image-18.jpg)
Average case Inner loop stops when A[i] <= key i j 1 sorted • • 9/14/2021 Key Array in random order S = j=1. . n tj tj = j / 2 in average S = j=1. . n j/2 = ½ j=1. . n j = n (n+1) / 4 = Θ (n 2) 18

Analyzing recursive algorithms • Defining recurrence relation • Solving recurrence relation – Recursion tree (iteration) method – Substitution method – Master method 9/14/2021 19
![Analyzing merge sort Tn MERGESORT A1 n Θ1 1 If n 1 Analyzing merge sort T(n) MERGE-SORT A[1. . n] Θ(1) 1. If n = 1,](https://slidetodoc.com/presentation_image_h2/a5861d745be0a032aca3b74587c18312/image-20.jpg)
Analyzing merge sort T(n) MERGE-SORT A[1. . n] Θ(1) 1. If n = 1, done. 2 T(n/2) 2. Recursively sort A[ 1. . n/2 ] and A[ n/2 +1. . n ]. f(n) 3. “Merge” the 2 sorted lists T(n) = 2 T(n/2) + Θ(n) 9/14/2021 20
![Recursive Insertion Sort Recursive Insertion SortA1 n 1 if n 1 do Recursive Insertion Sort Recursive. Insertion. Sort(A[1. . n]) 1. if (n == 1) do](https://slidetodoc.com/presentation_image_h2/a5861d745be0a032aca3b74587c18312/image-21.jpg)
Recursive Insertion Sort Recursive. Insertion. Sort(A[1. . n]) 1. if (n == 1) do nothing; 2. Recursive. Insertion. Sort(A[1. . n-1]); 3. Find index i in A such that A[i] <= A[n] < A[i+1]; 4. Insert A[n] after A[i]; 9/14/2021 21
![Binary Search Binary Search A1 N value if N 0 return Binary Search Binary. Search (A[1. . N], value) { if (N == 0) return](https://slidetodoc.com/presentation_image_h2/a5861d745be0a032aca3b74587c18312/image-22.jpg)
Binary Search Binary. Search (A[1. . N], value) { if (N == 0) return -1; // not found mid = (1+N)/2; if (A[mid] == value) return mid; // found else if (A[mid] > value) return Binary. Search (A[1. . mid-1], value); else return Binary. Search (A[mid+1, N], value) } 9/14/2021 22

Recursion tree Solve T(n) = 2 T(n/2) + n. n n n/2 n/4 (1) n/4 n … … h = log n n/4 n #leaves = n (n) Total (n log n) 9/14/2021 23

Substitution method • Recurrence: T(n) = 2 T(n/2) + n. • Guess: T(n) = O(n log n). (eg. by recursion tree method) • To prove, have to show T(n) ≤ c n log n for some c > 0 and for all n > n 0 • Proof by induction: assume it is true for T(n/2), prove that it is also true for T(n). This means: • Fact: T(n) = 2 T(n/2) + n • Assumption: T(n/2)≤ cn/2 log (n/2) • Need to Prove: T(n)≤ c n log (n) 9/14/2021 24

Proof • To prove T(n) = O(n log n), we need to show that T(n) cn logn for some positive c and all sufficiently large n. • Let’s assume this inequality is true for T(n/2), which means T(n/2) cn/2 log(n/2) • Substitute T(n/2) in the recurrence by the r. h. s. of the above inequality, we have T(n) = 2 T(n/2) + n 2 * cn/2 log (n/2) + n cn (log n – 1) + n cn log n – (cn – n) cn log n for c ≥ 1 and all n ≥ 0. Therefore, by definition, T(n) = O(n log n). 9/14/2021 25

Master theorem T(n) = a T(n/b) + f (n) Key: compare f(n) with nlogba CASE 1: f (n) = O(nlogba – e) T(n) = (nlogba). CASE 2: f (n) = (nlogba) T(n) = (nlogba log n). CASE 3: f (n) = (nlogba + e) and a f (n/b) c f (n) T(n) = ( f (n)). Regularity Condition Optional: extended case 2 9/14/2021 26

Analysis of Quick Sort 9/14/2021 27

Quick sort • Another divide and conquer sorting algorithm – like merge sort • Anyone remember the basic idea? • The worst-case and average-case running time? • Learn some new algorithm analysis tricks 9/14/2021 28

Quick sort Quicksort an n-element array: 1. Divide: Partition the array into two subarrays around a pivot x such that elements in lower subarray x elements in upper subarray. x x ≥x 2. Conquer: Recursively sort the two subarrays. 3. Combine: Trivial. Key: Linear-time partitioning subroutine. 9/14/2021 29

Partition • All the action takes place in the partition() function – Rearranges the subarray in place – End result: two subarrays • All values in first subarray all values in second – Returns the index of the “pivot” element separating the two subarrays p x 9/14/2021 r q x ≥x 30

Pseudocode for quicksort QUICKSORT(A, p, r) if p < r then q PARTITION(A, p, r) QUICKSORT(A, p, q– 1) QUICKSORT(A, q+1, r) Initial call: QUICKSORT(A, 1, n) 9/14/2021 31

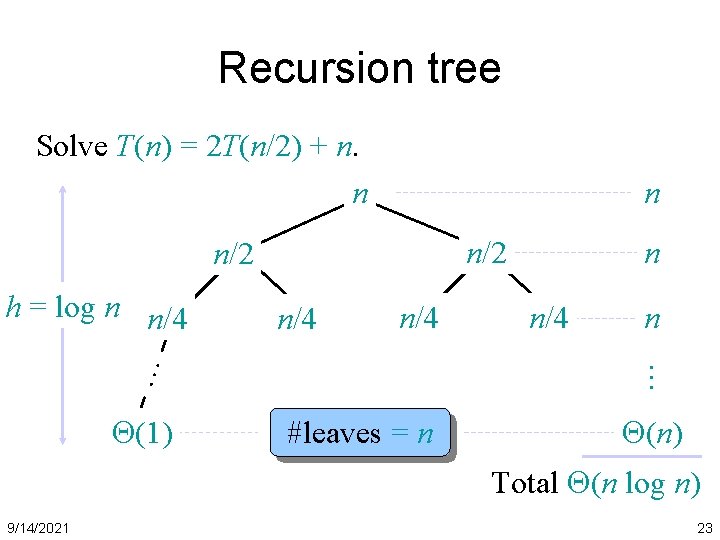
Idea of partition • If we are allowed to use a second array, it would be easy 9/14/2021 6 10 5 8 13 3 2 11 6 5 3 2 11 13 8 10 2 5 3 6 11 13 8 10 32

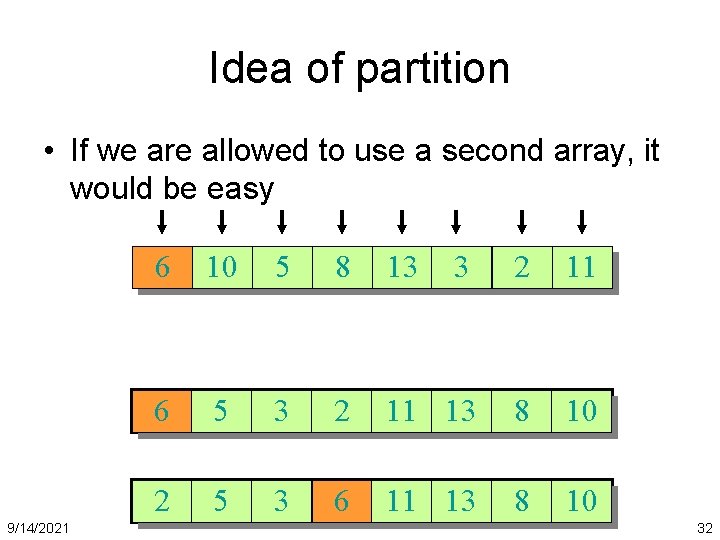
Another idea • Keep two iterators: one from head, one from tail 9/14/2021 6 10 5 8 13 3 2 11 6 2 5 3 13 8 10 11 3 2 5 6 13 8 10 11 33

In-place Partition 36 9/14/2021 10 2 5 638 13 83 2 11 10 34

Partition In Words • Partition(A, p, r): – Select an element to act as the “pivot” (which? ) – Grow two regions, A[p. . i] and A[j. . r] • All elements in A[p. . i] <= pivot • All elements in A[j. . r] >= pivot – – – 9/14/2021 Increment i until A[i] > pivot Decrement j until A[j] < pivot Swap A[i] and A[j] Note: different from book’s Repeat until i >= j partition(), which uses two Swap A[j] and A[p] iterators that both move forward. Return j 35
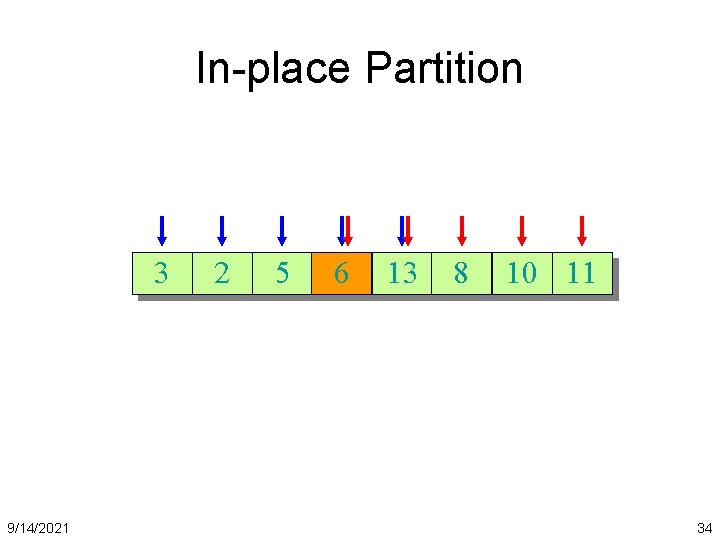
![Partition Code PartitionA p r x Ap pivot is the first element Partition Code Partition(A, p, r) x = A[p]; // pivot is the first element](https://slidetodoc.com/presentation_image_h2/a5861d745be0a032aca3b74587c18312/image-36.jpg)
Partition Code Partition(A, p, r) x = A[p]; // pivot is the first element i = p; j = r + 1; while (TRUE) { repeat i++; until A[i] > x or i >= j; repeat What is the running time of j--; until A[j] < x or j < i; partition()? if (i < j) Swap (A[i], A[j]); else break; partition() runs in (n) time } swap (A[p], A[j]); return j; 9/14/2021 36

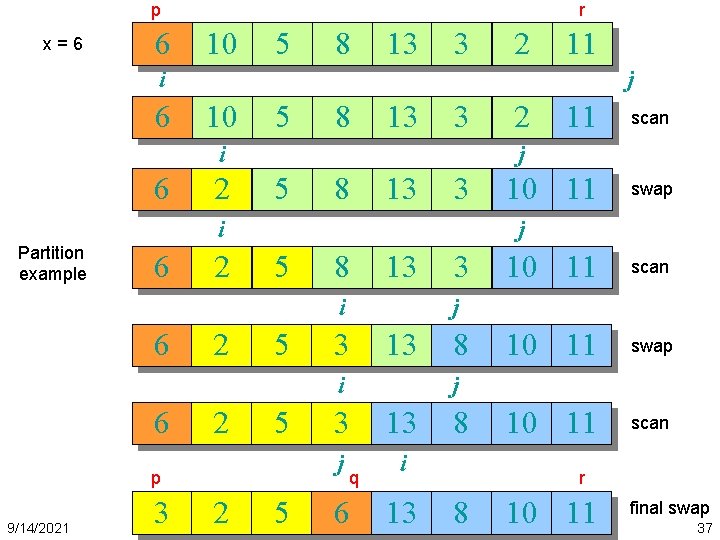
p x=6 6 r 10 5 8 13 3 2 11 i 6 j 10 5 8 13 3 i 6 2 5 8 13 3 2 5 5 p 9/14/2021 3 2 10 11 swap 5 3 10 11 scan 10 11 swap 10 11 scan j 3 13 i 6 scan j i 6 11 j i Partition example 2 8 j 3 13 j i q 6 13 8 r 8 10 11 final swap 37

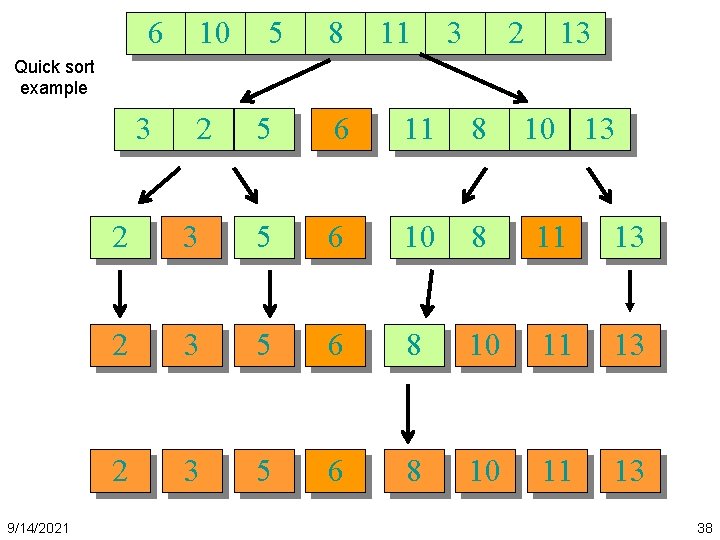
6 10 5 8 11 3 2 13 Quick sort example 3 9/14/2021 2 5 6 11 8 10 13 2 3 5 6 10 8 11 13 2 3 5 6 8 10 11 13 38

Analysis of quicksort • Assume all input elements are distinct. • In practice, there are better partitioning algorithms for when duplicate input elements may exist. • Let T(n) = worst-case running time on an array of n elements. 9/14/2021 39

Worst-case of quicksort • Input sorted or reverse sorted. • Partition around min or max element. • One side of partition always has no elements. (arithmetic series) 9/14/2021 40

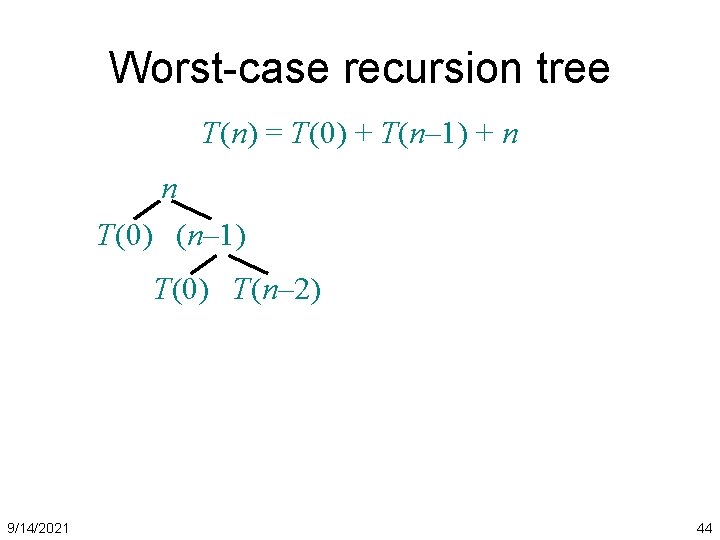
Worst-case recursion tree T(n) = T(0) + T(n– 1) + n 9/14/2021 41

Worst-case recursion tree T(n) = T(0) + T(n– 1) + n T(n) 9/14/2021 42

Worst-case recursion tree T(n) = T(0) + T(n– 1) + n n T(0) T(n– 1) 9/14/2021 43

Worst-case recursion tree T(n) = T(0) + T(n– 1) + n n T(0) (n– 1) T(0) T(n– 2) 9/14/2021 44

Worst-case recursion tree T(n) = T(0) + T(n– 1) + n n T(0) (n– 1) T(0) (n– 2) T(0) 9/14/2021 45

Worst-case recursion tree T(n) = T(0) + T(n– 1) + n n T(0) (n– 1) height = n height T(0) (n– 2) T(0) 9/14/2021 46

Worst-case recursion tree T(n) = T(0) + T(n– 1) + n n T(0) (n– 1) height = n n T(0) (n– 2) T(0) 9/14/2021 47

Worst-case recursion tree T(n) = T(0) + T(n– 1) + n n (1) (n– 2) height = n (1) n T(n) = (n) + (n 2) = (n 2) (1) 9/14/2021 48

Best-case analysis (For intuition only!) If we’re lucky, PARTITION splits the array evenly: T(n) = 2 T(n/2) + (n) = (n log n) (same as merge sort) What if the split is always ? What is the solution to this recurrence? 9/14/2021 49

Analysis of “almost-best” case 9/14/2021 50

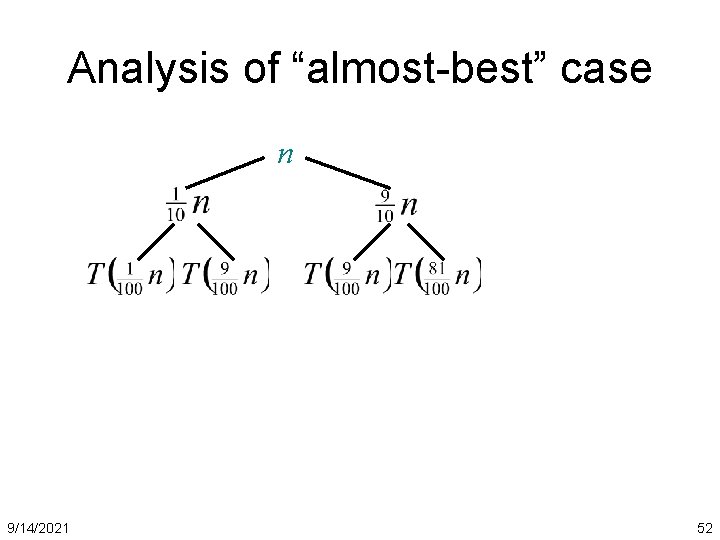
Analysis of “almost-best” case n 9/14/2021 51

Analysis of “almost-best” case n 9/14/2021 52

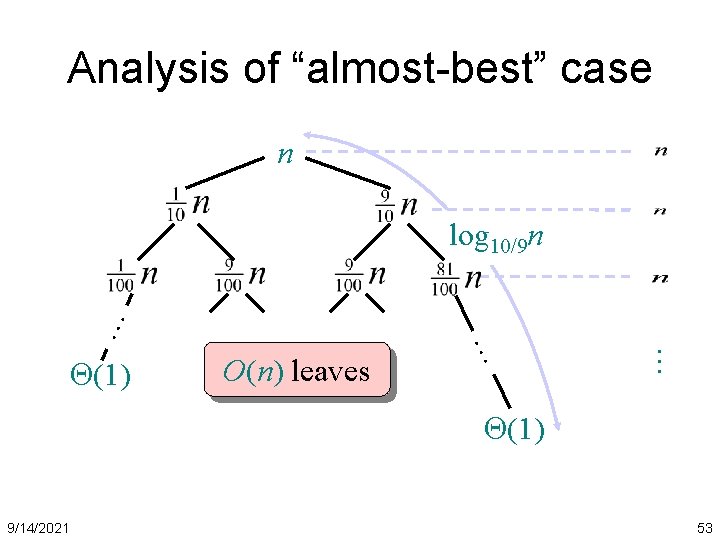
Analysis of “almost-best” case n O(n) leaves … (1) … … log 10/9 n (1) 9/14/2021 53

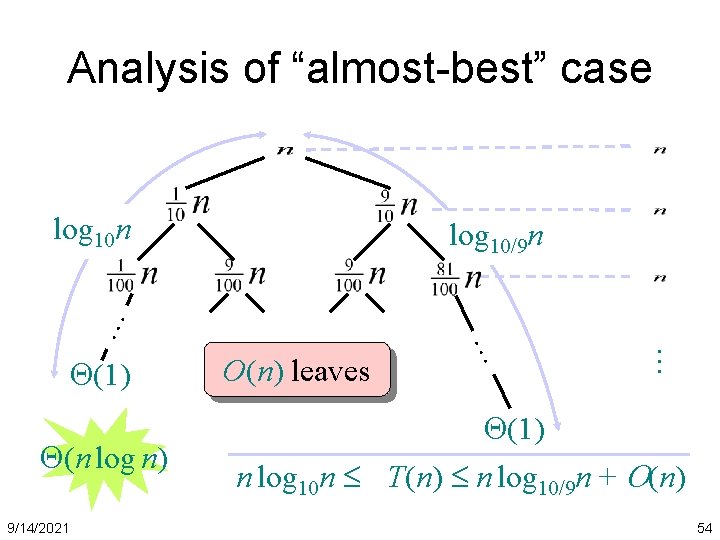
Analysis of “almost-best” case log 10 n (n log n) 9/14/2021 O(n) leaves … (1) … … log 10/9 n (1) n log 10 n T(n) n log 10/9 n + O(n) 54

Quicksort Runtimes • Best-case runtime Tbest(n) (n log n) • Worst-case runtime Tworst(n) (n 2) • Worse than mergesort? Why is it called quicksort then? • Its average runtime Tavg(n) (n log n ) • Better even, the expected runtime of randomized quicksort is (n log n) 9/14/2021 55

Randomized quicksort • Randomly choose an element as pivot – Every time need to do a partition, throw a die to decide which element to use as the pivot – Each element has 1/n probability to be selected Rand-Partition(A, p, r) d = random(); // a random number between 0 and 1 index = p + floor((r-p+1) * d); // p<=index<=r swap(A[p], A[index]); Partition(A, p, r); // now do partition using A[p] as pivot 9/14/2021 56

Running time of randomized quicksort T(n) = T(0) + T(n– 1) + dn T(1) + T(n– 2) + dn M T(n– 1) + T(0) + dn if 0 : n– 1 split, if 1 : n– 2 split, if n– 1 : 0 split, • The expected running time is an average of all cases Expectation 9/14/2021 57
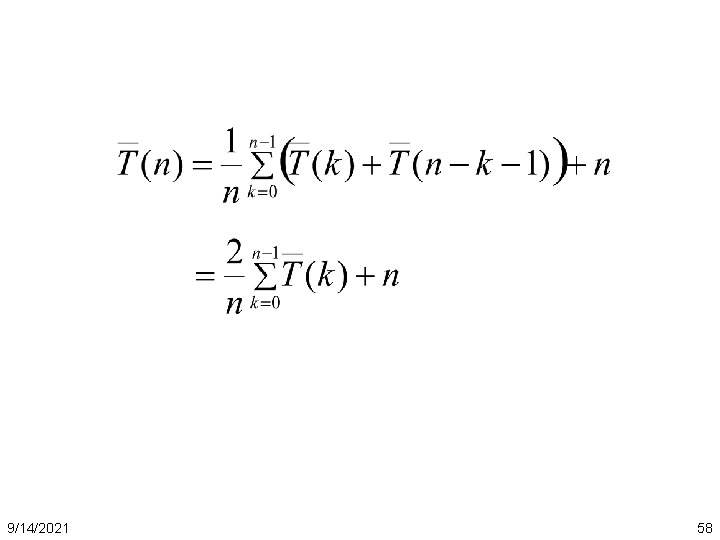
9/14/2021 58

Solving recurrence 1. Recursion tree (iteration) method - Good for guessing an answer 2. Substitution method - Generic method, rigid, but may be hard 3. Master method - Easy to learn, useful in limited cases only - Some tricks may help in other cases 9/14/2021 59

Substitution method The most general method to solve a recurrence (prove O and separately): 1. Guess the form of the solution: (e. g. using recursion trees, or expansion) 2. Verify by induction (inductive step). 9/14/2021 60

Expected running time of Quicksort • Guess • We need to show that for some c and sufficiently large n • Use T(n) instead of for convenience 9/14/2021 61

• Fact: • Need to show: T(n) ≤ c n log (n) • Assume: T(k) ≤ ck log (k) for 0 ≤ k ≤ n-1 • Proof: using the fact that if c ≥ 4. Therefore, by defintion, T(n) = (nlogn) 9/14/2021 62

Tightly Bounding The Key Summation Split the summation for a What we doing here? tighterare bound The lg are k inwe thedoing second term What here? is bounded by lg n Whatthe arelgwen doing here? Move outside the summation 9/14/2021 63

Tightly Bounding The Key Summation The summation bound so far The lg k in the first term is What are we doing here? bounded by lg n/2 = lg n we - 1 doing here? What are Move (lg n - 1) outside the What are we doing here? summation 9/14/2021 64

Tightly Bounding The Key Summation The summation bound so far Distribute the (lg nhere? - 1) What are we doing The summations overlap in What are we doing here? range; combine them The. What Guassian are weseries doing here? 9/14/2021 65

Tightly Bounding The Key Summation The summation bound so far Rearrange first term, place What are we doing here? upper bound on second Guassian series What are we doing? Multiply it What are we doing? all out 9/14/2021 66

Tightly Bounding The Key Summation 9/14/2021 67