CS 3343 Analysis of Algorithms Lecture 5 Solving

CS 3343: Analysis of Algorithms Lecture 5: Solving recurrence by recursion-tree method 2/23/2021 1

Problem of the day • How many multiplications do you need to compute 316? 316 =3 x 3 …. x 3 Answer: 15 316 =38 x 38 38 =34 x 34 34 =32 x 32 Answer: 4 32 =3 x 3 2/23/2021 2

Pseudo code int pow (b, n) // compute bn m = n >> 1; p = pow (b, m); p = p * p; if (n % 2) return p * b; else return p; 2/23/2021 3

Pseudo code int pow (b, n) m = n >> 1; p = pow (b, m); p = p * p; if (n % 2) return p * b; else return p; 2/23/2021 int pow (b, n) m = n >> 1; p = pow(b, m) * pow(b, m); if (n % 2) return p * b; else return p; 4

Outline • Review of last lecture – analyzing recursive algorithms – Defining recurrence relation • Today: analyzing recursive algorithms – Solving recurrence relation 2/23/2021 5

Analyzing merge sort T(n) MERGE-SORT A[1. . n] Θ(1) 1. If n = 1, done. 2 T(n/2) 2. Recursively sort A[ 1. . n/2 ] and A[ n/2 +1. . n ]. f(n) 3. “Merge” the 2 sorted lists Sloppiness: Should be T( n/2 ) + T( n/2 ) , but it turns out not to matter asymptotically. 2/23/2021 6

Recurrence for merge sort 1. Divide: Trivial. 2. Conquer: Recursively sort 2 subarrays. 3. Combine: Merge two sorted subarrays T(n) = 2 T(n/2) + Θ(n) # subproblems subproblem size 2/23/2021 Dividing and Combining 7

Binary Search Binary. Search (A[1. . N], value) { if (N == 0) return -1; // not found mid = (1+N)/2; if (A[mid] == value) return mid; // found else if (A[mid] > value) return Binary. Search (A[1. . mid-1], value); else return Binary. Search (A[mid+1, N], value) } 2/23/2021 8

Recursive Insertion Sort Recursive. Insertion. Sort(A[1. . n]) 1. if (n == 1) do nothing; 2. Recursive. Insertion. Sort(A[1. . n-1]); 3. Find index i in A such that A[i] <= A[n] < A[i+1]; 4. Insert A[n] after A[i]; 2/23/2021 9

Compute factorial Factorial (n) if (n == 1) return 1; return n * Factorial (n-1); • Note: here we use n as the size of the input. However, usually for such algorithms we would use log(n), i. e. , the bits needed to represent n, as the input size. 2/23/2021 10

Recurrence for computing power int pow (b, n) m = n >> 1; p = pow (b, m); p = p * p; if (n % 2) return p * b; else return p; T(n) = ? 2/23/2021 int pow (b, n) m = n >> 1; p=pow(b, m)*pow(b, m); if (n % 2) return p * b; else return p; T(n) = ? 11

Recurrence for computing power int pow (b, n) m = n >> 1; p = pow (b, m); p = p * p; if (n % 2) return p * b; else return p; T(n) = T(n/2)+ (1) 2/23/2021 int pow (b, n) m = n >> 1; p=pow(b, m)*pow(b, m); if (n % 2) return p * b; else return p; T(n) = 2 T(n/2)+ (1) 12

What do they mean? Challenge: how to solve the recurrence to get a closed form, e. g. T(n) = Θ (n 2) or T(n) = Θ(nlgn), or at least some bound such as T(n) = O(n 2)? 2/23/2021 13

Solving recurrence • Running time of many algorithms can be expressed in one of the following two recursive forms or Both can be very hard to solve. We focus on relatively easy ones, which you will encounter frequently in many real algorithms (and exams…) 2/23/2021 14

Solving recurrence 1. Recursion tree or iteration method - Good for guessing an answer 2. Substitution method - Generic method, rigid, but may be hard 3. Master method - Easy to learn, useful in limited cases only - Some tricks may help in other cases 2/23/2021 15

Recurrence for merge sort T(n) = (1) if n = 1; 2 T(n/2) + (n) if n > 1. We will usually ignore the base case, assuming it is always a constant (but not 0). 2/23/2021 16

Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. 2/23/2021 17

Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. T(n) 2/23/2021 18

Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn T(n/2) 2/23/2021 T(n/2) 19

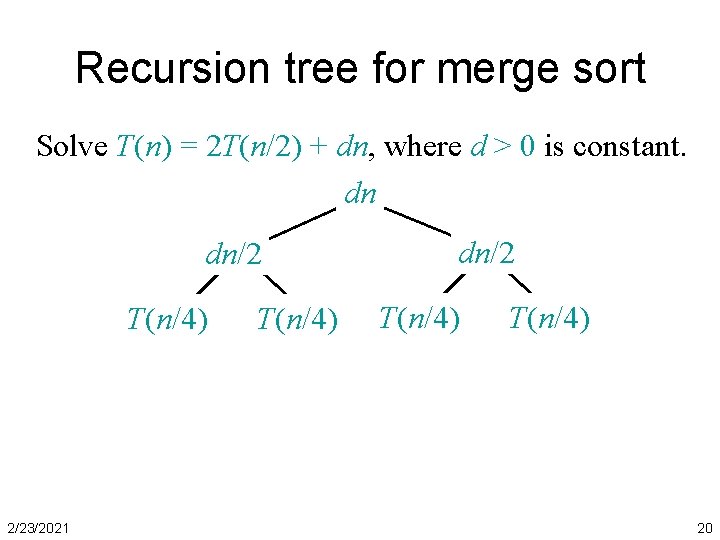
Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn/2 T(n/4) 2/23/2021 T(n/4) dn/2 T(n/4) 20

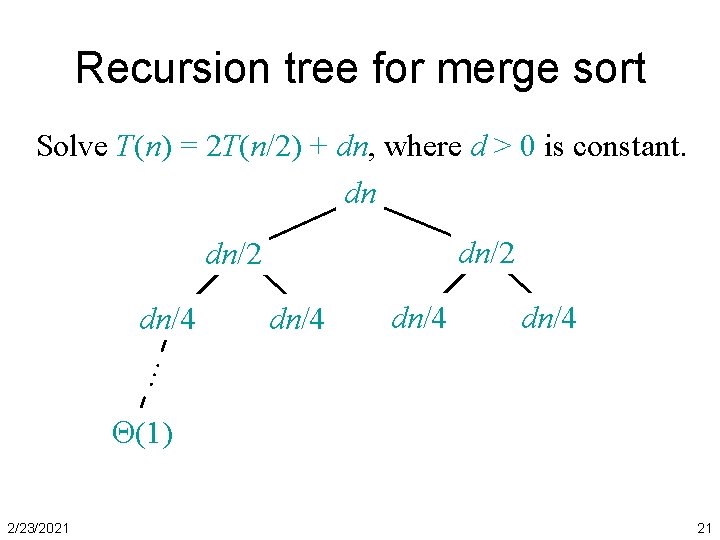
Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn/2 dn/4 … dn/4 (1) 2/23/2021 21

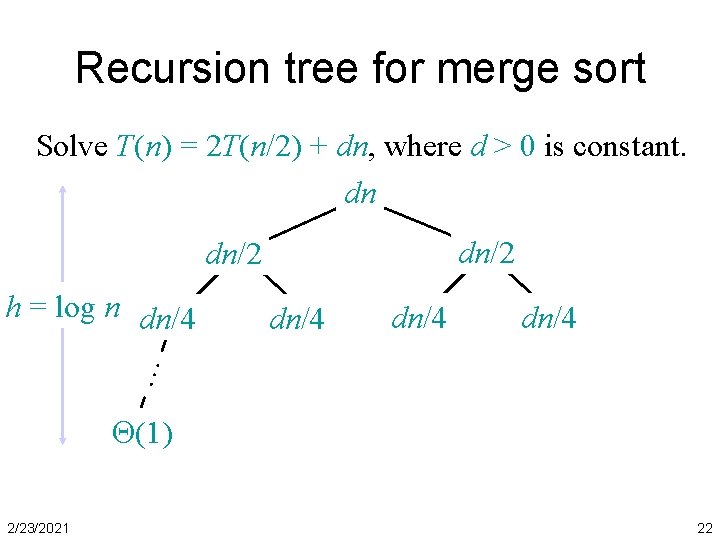
Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn/2 dn/4 … h = log n dn/4 (1) 2/23/2021 22

Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn dn/2 dn/4 … h = log n dn/4 (1) 2/23/2021 23

Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn dn/2 dn/4 … h = log n dn/4 dn (1) 2/23/2021 24

Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn … h = log n dn/4 dn … dn/2 (1) 2/23/2021 25

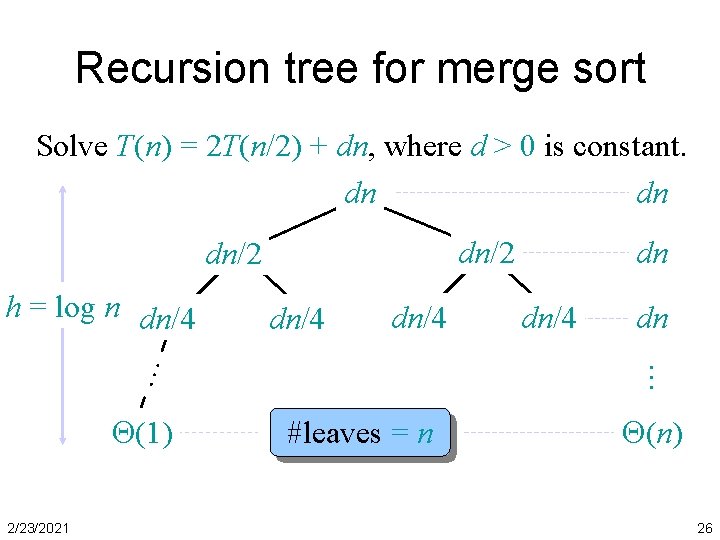
Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn dn/2 dn/4 (1) 2/23/2021 dn/4 dn … … h = log n dn/4 dn #leaves = n (n) 26

Recursion tree for merge sort Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn dn/2 dn/4 (1) #leaves = n Later we will usually ignore d 2/23/2021 dn/4 dn … … h = log n dn/4 dn (n) Total (n log n) 27

Recurrence for computing power int pow (b, n) m = n >> 1; p = pow (b, m); p = p * p; if (n % 2) return p * b; else return p; T(n) = T(n/2)+ (1) 2/23/2021 int pow (b, n) m = n >> 1; p=pow(b, m)*pow(b, m); if (n % 2) return p * b; else return p; T(n) = 2 T(n/2)+ (1) Which algorithm is more efficient asymptotically? 28

Time complexity for Alg 1 Solve T(n) = T(n/2) + 1 • T(n) = T(n/2) + 1 = T(n/4) + 1 = T(n/8) + 1 + 1 = T(1) + 1 + … + 1 = Θ (log(n)) log(n) Iteration method 2/23/2021 29

Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 2/23/2021 30

Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. T(n) 2/23/2021 31

Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 1 T(n/2) 2/23/2021 T(n/2) 32

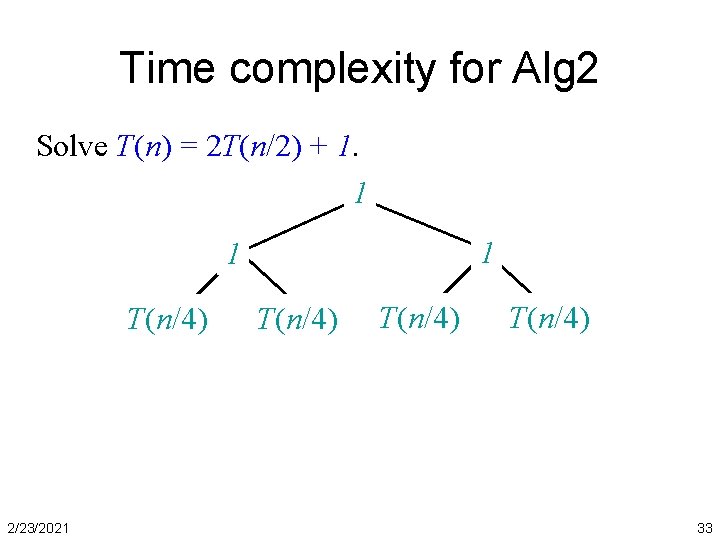
Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 1 1 1 T(n/4) 2/23/2021 T(n/4) 33

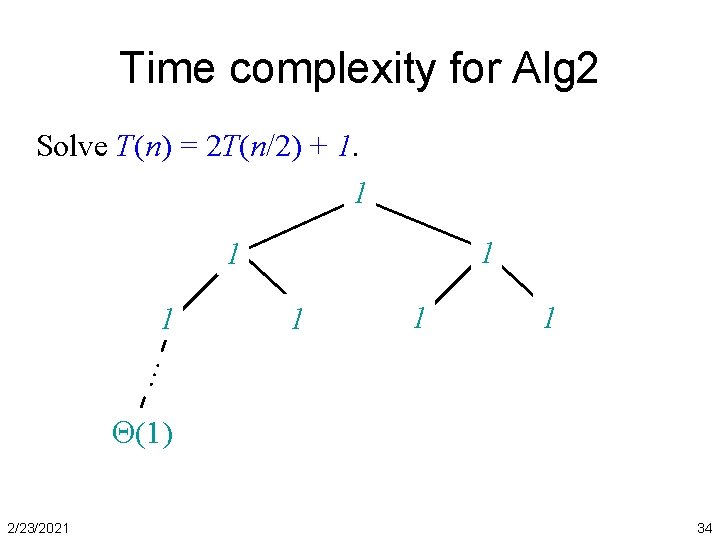
Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 1 1 1 … 1 (1) 2/23/2021 34

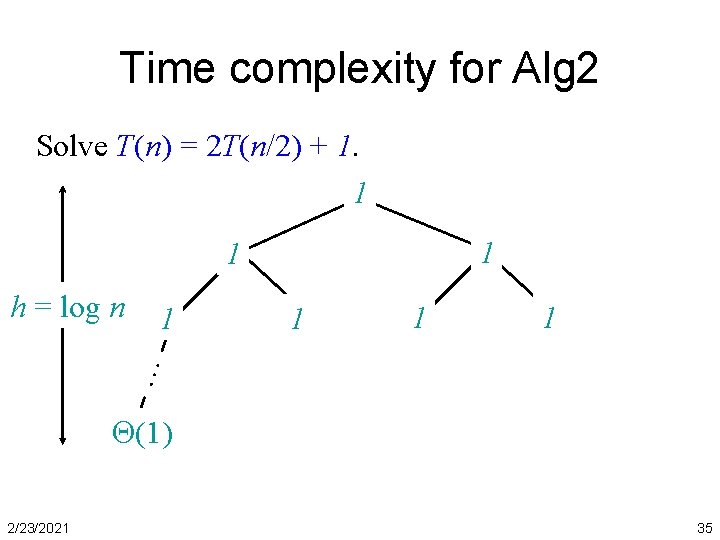
Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 1 1 1 1 … h = log n (1) 2/23/2021 35

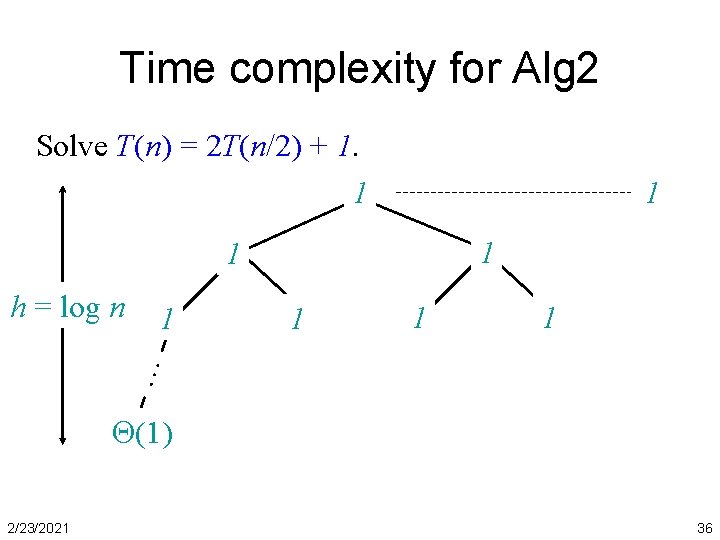
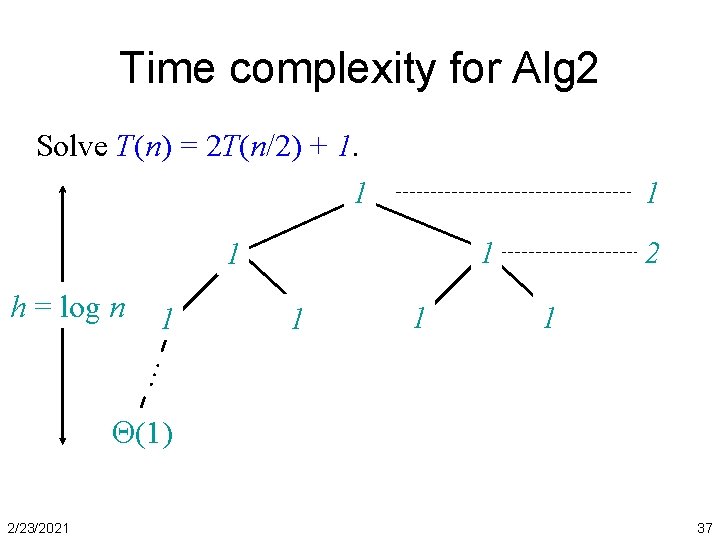
Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 1 1 1 1 … h = log n (1) 2/23/2021 36

Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 1 1 1 1 … h = log n 2 (1) 2/23/2021 37

Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 1 1 1 … h = log n 1 1 2 1 4 … 1 1 (1) 2/23/2021 38

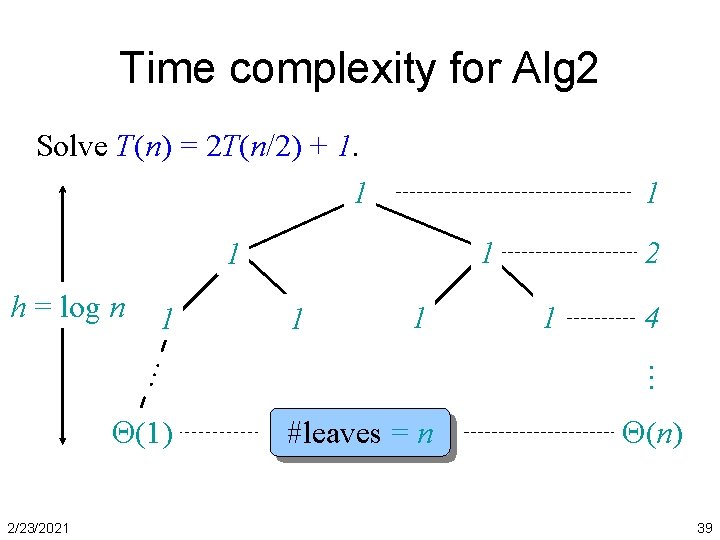
Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 1 1 1 1 (1) 2/23/2021 1 4 … … h = log n 2 #leaves = n (n) 39

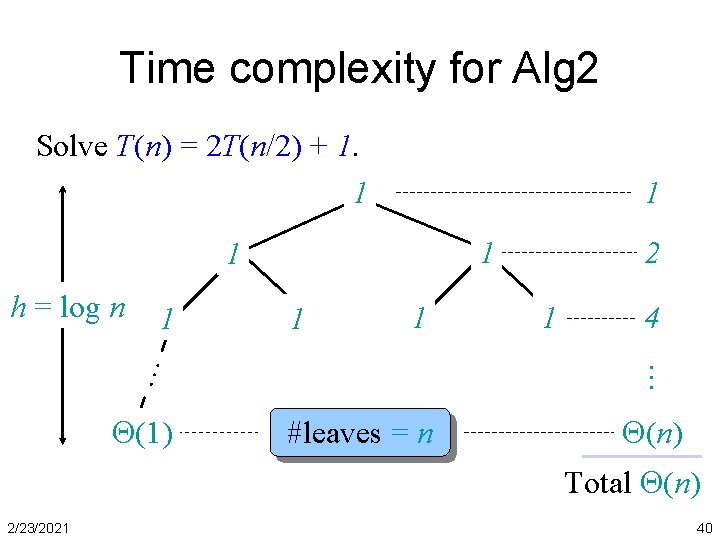
Time complexity for Alg 2 Solve T(n) = 2 T(n/2) + 1. 1 1 1 1 (1) 1 4 … … h = log n 2 #leaves = n (n) Total (n) 2/23/2021 40

More iteration method examples • T(n) = T(n-1) + 1 = T(n-2) + 1 = T(n-3) + 1 + 1 = T(1) + 1 + … + 1 = Θ (n) 2/23/2021 n-1 41

More iteration method examples • T(n) = T(n-1) + n = T(n-2) + (n-1) + n = T(n-3) + (n-2) + (n-1) + n = T(1) + 2 + 3 + … + n = Θ (n 2) 2/23/2021 42

3 -way-merge-sort (A[1. . n]) If (n <= 1) return; 3 -way-merge-sort(A[1. . n/3]); 3 -way-merge-sort(A[n/3+1. . 2 n/3]); 3 -way-merge-sort(A[2 n/3+1. . n]); Merge A[1. . n/3] and A[n/3+1. . 2 n/3]; Merge A[1. . 2 n/3] and A[2 n/3+1. . n]; • Is this algorithm correct? • What’s the recurrence function for the running time? • What does the recurrence function solve to? 2/23/2021 43

Unbalanced-merge-sort ub-merge-sort (A[1. . n]) if (n<=1) return; ub-merge-sort(A[1. . n/3]); ub-merge-sort(A[n/3+1. . n]); Merge A[1. . n/3] and A[n/3+1. . n]. • Is this algorithm correct? • What’s the recurrence function for the running time? • What does the recurrence function solve to? 2/23/2021 44

More recursion tree examples (1) • • • 2/23/2021 T(n) = 3 T(n/3) + n T(n) = T(n/3) + T(2 n/3) + n T(n) = 2 T(n/4) + n 2 T(n) = 3 T(n/2) + n 2 45

More recursion tree examples (2) • • 2/23/2021 T(n) = T(n-2) + n T(n) = T(n-2) + 1 T(n) = 2 T(n-2) + n T(n) = 2 T(n-2) + 1 46