CS 3291 Digital Signal Processing 05 06 Section

CS 3291 : Digital Signal Processing '05 -06 Section 3 : Discrete-time LTI systems 3. 1 Introduction: A discrete time system takes discrete time input signal { x[ n ] }, & produces an output signal { y[ n ] }. Oct'04 CS 3291 1

• Implemented by general purpose computer, microcomputer or dedicated digital hardware capable of carrying out arithmetic operations on samples of {x[n]} and {y[n]}. • {x[n]} is sequence whose value at t=n. T is x[n]. • Similarly for {y[n]}. • T is sampling interval in seconds. • 1/T is sampling frequency in Hz. • {x[n-N]} is sequence whose value at t=n. T is x[n-N]. {x[n-N]} is {x[n]} with every sample delayed by N sampling intervals. • Many types of discrete time system can be considered, e. g. Oct'04 CS 3291 2

(i) Discrete time "amplifier" with output: y[n] = A. x[n]. • Described by "difference equation": y[n] = A x[n]. • Represented in diagram form by a "signal flow graph”. x[n] Oct'04 A y[n] CS 3291 3

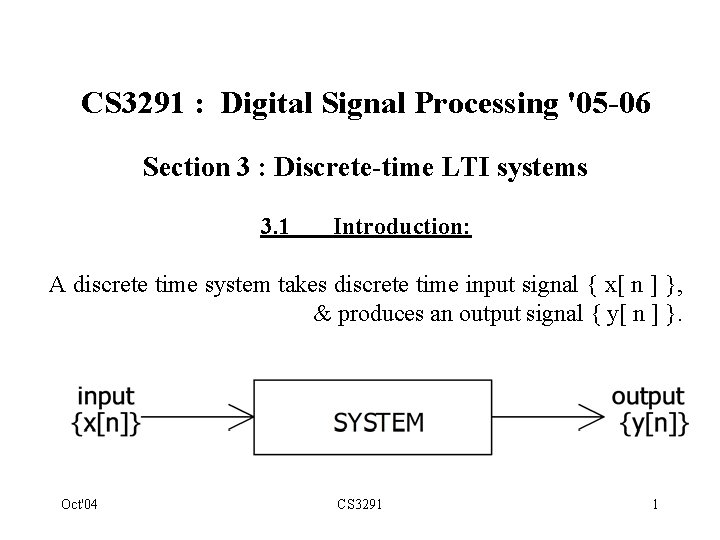
(ii) Processing system whose output at t=n. T is obtained by weighting & summing present & previous input samples: y[n] = A 0 x[n] + A 1 x[n-1] + A 2 x[n-2] + A 3 x[n-3] + A 4 x[n-4] ‘Non-recursive difference equatn’ with signal flow graph below. Boxes marked " z -1 " produce a delay of one sampling interval. Oct'04 CS 3291 4

(iii) System whose output y[n] at t = n. T is calculated according to the following recursive difference equation: y[n] = A 0 x[n] - B 1 y[n-1] whose signal flow graph is given below. • Recursive means that previous values of y[n] as well as present & previous values of x[n] are used to calculate y[n]. x[n] A 0 y[n] B 1 Oct'04 CS 3291 z-1 5

(iv) A system whose output at t=n. T is: y[n] = (x[n]) 2 as represented below. y[n] x[n] Oct'04 CS 3291 6

3. 2. LTI Systems: To be LTI, a discrete-time system must satisfy: (I) Linearity ( Superposition ): • Given any two discrete time signals {x 1 [n]} & {x 2 [n]}, if {x 1 [n]} {y 1 [n]} & {x 2 [n]} {y 2 [n]} then for any values of k 1 and k 2 , response to k 1{x 1[n]} + k 2{x 2[n]} must be k 1{y 1[n]} + k 2 {y 2 [n]}. • To multiply a sequence by k, multiply each element by k, k{x[n]} = {k x[n]}. • To add two sequences together, add corresponding samples, {x[n]} + {y[n]} = {x[n] + y[n]}. ) Oct'04 CS 3291 7

(II) Time-invariance : • Given any discrete time signal {x[n]}, if response to {x[n]} is {y[n]}, response to {x[n-N]} must be {y[n-N]} for any N. • Delaying input by N samples only delays output by N samples. • Examples (i), (ii) and (iii) are LTI whereas (iv) is not LTI. Oct'04 CS 3291 8

3. 3. Impulse-response: Useful to consider response of LTI systems to a discrete time unit impulse , or in short an impulse denoted by {d [n] } with: Oct'04 CS 3291 9

• {d[n-N]} is delayed impulse where the only non-zero sample occurs at n=N rather than at n=0. • When input is {d[n]}, output is impulse response {h[n]}. • If impulse-response of an LTI system is known, its response to any other input signal may be predicted. Oct'04 CS 3291 10

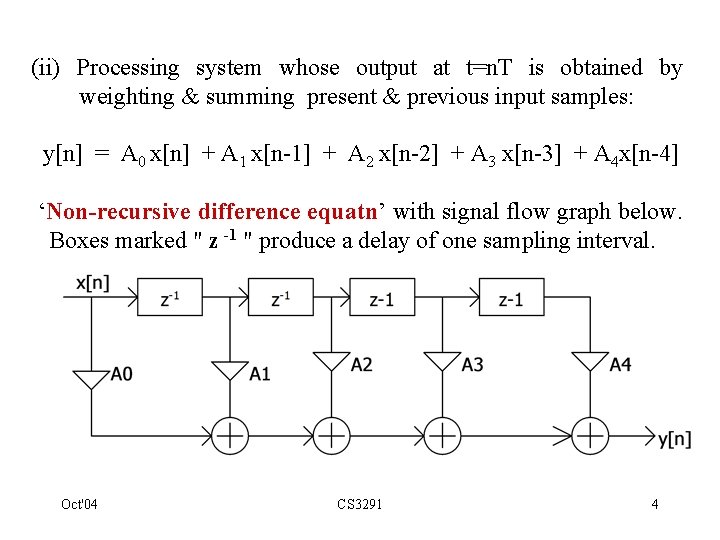
3. 4. Computing an impulse response: • Consider a discrete time system with signal-flow graph below with A 1, A 2, A 3, A 4, A 5 set to specific constants. • Notice the labels X 1, X 2, etc. • Realised by microcomputer running a program with flow-diagram & high-level language implementation as listed next. X 1 z-1 x[n] A 1 X 2 z-1 A 2 X 3 z-1 A 3 X 4 z-1 A 4 X 5 A 5 Y y[n] Oct'04 CS 3291 11

clear all; A 1=1; A 2=2; A 3=3; A 4=-4; A 5=5; Set A 1, A 2, …. x 1=0; x 2=0; x 3=0; x 4=0; x 5=0; Zero X 1, X 2, X 3, X 4, X 5 while ~isempty(X) X = input( 'X = '); x 1 = X; INPUT X Y= A 1*x 1 + A 2*x 2 + A 3*x 3 Y = A 1*X + A 2*X 2 + A 3*X 3 +. . . + A 4*x 4 + A 5*x 5 ; OUTPUT Y disp([' Y = ' num 2 str(Y)]); X 5 = X 4; X 4 = X 3; X 3 = X 2; X 2 =X 1 x 5 = x 4 ; x 4 = x 3; x 3 = x 2 ; x 2 =x 1; end; % MATLAB program Oct'04 CS 3291 12

Here is another version using MATLAB arrays: A = [1 2 3 -4 5 ] ; x = [0 0 0 ] ; while 1 X = input( 'X = '); x(1)=X; Y=A(1) * X; for k = 2 : 5 Y = Y + A(k)*x(k); end; disp([' Y = ' num 2 str(Y)]); for k=5: -1: 2 x(k) = x(k-1); end; Oct'04 CS 3291 13

And an even more efficient version A = [1 2 3 -4 5 ] ; x = [0 0 0 ] ; while 1 x(1) = input( 'X = '); Y = A(1)*x(1); for k = 5 : -1: 2 Y = Y + A(k)*x(k); x(k) = x(k-1); end; disp([' Y = ' num 2 str(Y)]); end; Oct'04 CS 3291 14

• These can be run in MATLAB • The ‘while 1’ statement initiates an infinite loop. • Program will run for ever or until interrupted by ‘CONTROL+C’ Oct'04 CS 3291 15

• Impulse-response for this example may be deduced by running program & entering values for X on the keyboard : 0, 0, 1, 0, 0, . . • Sequence of output samples printed out will be : 0, 0, A 1, A 2, A 3, A 4, A 5, 0, . . • Impulse-response can also be obtained by tabulation (later). • Output must be zero until input becomes equal to 1 at n=0 • Impulse response is: {. . . , 0, A 1, A 2, A 3, A 4, A 5, 0, 0, . . . } where the sample at n=0 is underlined. • Only five non-zero output samples are observed. • This is a " finite impulse-response ” (FIR). Oct'04 CS 3291 16

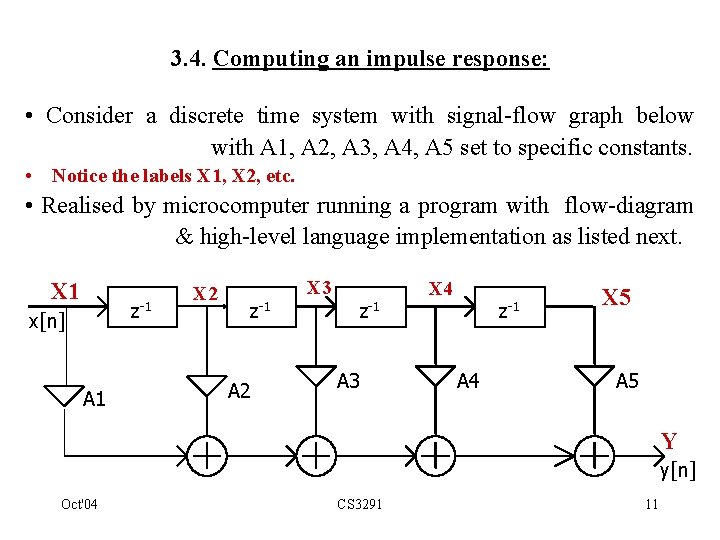
Exercise 3. 1: Calculate impulse-responses for difference equations: (i) y[n] = x[n] + 2 x[n-1] + 3 x[n-2] - 4 x[n-3] + 5 x[n-4] (ii) y[n] = 4 x[n] - 0. 5 y[n-1] Solutions: • If computer not available we may use a tabulation. • Difference eqn (i) will produce a finite impulse-response. • Difference eqn (ii) produces infinite response whose samples gradually reduce in amplitude but never quite become zero. Oct'04 CS 3291 17

(i) y[n] = x[n] + 2 x[n-1] + 3 x[n-2] - 4 x[n-3] + 5 x[n-4] n x[n] x[n-1] x[n-2] x[n-3] x[n-4] y[n] -1 0 0 0 0 0 1 1 0 0 0 2 2 0 0 1 0 0 3 3 0 0 0 1 0 -4 4 0 0 1 5 5 0 0 0 : : : : Solution is: - {. . 0, . . , 0, 1, 2, 3, -4, 5, 0, . . . } Oct'04 CS 3291 18

Difference equation (ii): y[n] = 4 x[n] - 0. 5 y[n-1] n x[n] y[n-1] y[n] 0 1 0 4 1 0 4 -2 2 0 -2 1 3 0 1 -0. 5 4 0 -0. 5 0. 25 5 0 0. 25 -0. 125 : : : : Solution is: {. . , 0, 4, -2, 1, -0. 5, 0. 25, -0. 125, . . . ) Oct'04 CS 3291 19

3. 5. Digital filters: • A "digital filter” is a digitally implemented LTI discrete time system governed by a difference equation of finite order; e. g. : (i) y[n] = x[n] + 2 x[n-1] + 3 x[n-2] - 4 x[n-3] + 5 x[n-4] (ii) y[n] = 4 x[n] - 0. 5 y[n-1] • Difference equation (i) is "non-recursive" & produces a finite impulse response (FIR). • Difference equation (ii) is " recursive ". • Impulse-response of a recursive difference equation can have an infinite number of non-zero terms. In this case it is an infinite impulse-response (IIR). Oct'04 CS 3291 20

• Next slide has yet another way of programming difference equations (i. e. digital filters) in MATLAB. • But this time, we use a MATLAB function and operate on a whole array of music at once. • You can find the music file ‘cap 4 th. wav’ in • www. cs. man. ac. uk/~barry/mydocs/CS 3291/MATLAB Oct'04 CS 3291 21

MATLAB function ‘filter’ used for non-recursive diffce eqn y = filter(A, 1, x) filters signal in array x to create array y. For each sample x(n) of array x: y(n) = A(1)*x(n) + A(2)*x(n-1) +. . . + A(N+1)*x(n-N) Example (i): y[n] = x[n] + 2 x[n-1] + 3 x[n-2] - 4 x[n-3] + 5 x[n-4] [x, fs, nbits] = wavread ('cap 4 th. wav'); sound(x, fs, nbits); pause; y = filter ( [1 2 3 -4 5], 1, x); sound(y, fs, nbits); Oct'04 CS 3291 22

Use of ‘filter’ for recursive difference equatn y = filter(A, B, x) filters signal in array x to create array y using a recursive difference equation. Example (ii): y[n] = 4 x[n] - 0. 5 y[n-1] [x, fs, nbits] = wavread ('cap 4 th. wav'); sound(x, fs, nbits); pause; y = filter ( [4], [1 0. 5], x); sound(y, fs, nbits); Oct'04 CS 3291 23

3. 6. Discrete time convolution: If impulse-response of an LTI system is {h[n]} its response to any input {x[n]} is an output {y[n] } whose samples are given by the following "convolution" formulae: Consider the response of a system with impulse response: {h[n]} = {. . . , 0, 1, 2, 3, -4, 5, 0, . . } to {x[n]} = {. . . 0, . . . , 0 , 1, 2, 3, 0, . . . . } Oct'04 CS 3291 24

• Result is not too surprising. • It is the difference equation for an LTI system whose impulse response is {. . , 0, 1, 2, 3, -4, 5, 0, . . }. • Program discussed earlier implements this difference equation, • We could complete the example by running it, entering samples of { x[n] }, and noting the output sequence. • Alternatively, we could use tabulation as follows: Oct'04 CS 3291 25

y[n] = x[n] + 2 x[n-1] + 3 x[n-2] - 4 x[n-3] + 5 x[n-4] n x[n] x[n-1] x[n-2] x[n-3] x[n-4] y[n] : : : : -1 0 0 0 0 1 00 0 0 1 1 2 10 0 0 4 2 3 21 0 0 10 3 0 32 1 0 8 4 0 03 2 1 6 5 0 00 3 2 -2 6 0 00 0 3 15 7 0 00 0 0 0 : : {y[n]} = {. . 0, . . . , 0, 1, 4, 10, 8, 6, -2, 15, 0, . . . . } Oct'04 CS 3291 26

3. 7. Proof of discrete time convolution formulae: Only use defns of linearity, time-invariance & impulse-response. Since d[n-m] is non-zero only at n = m, given any sequence {x[n]}, {x[n]} is sum of infinite number of delayed impulses{d[n-m]} each multiplied by a single element, x[m]. Response to {d[n-m]} is {h[n-m]} for any value of m. response to {x[n]} is : Oct'04 CS 3291 27

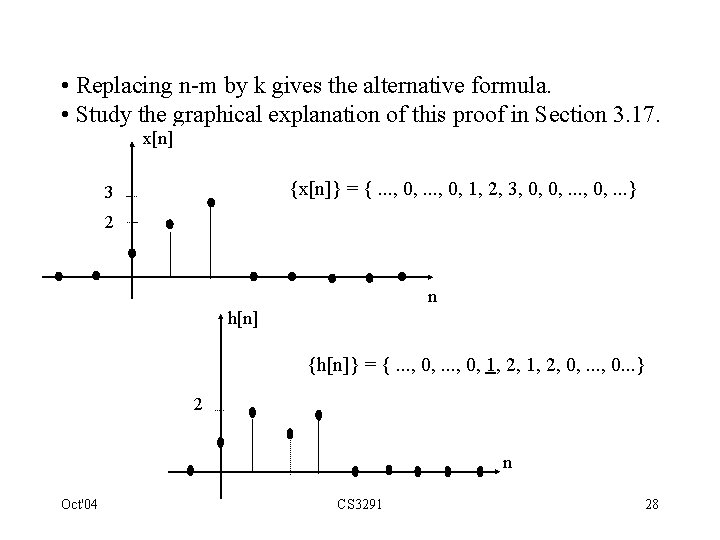
• Replacing n-m by k gives the alternative formula. • Study the graphical explanation of this proof in Section 3. 17. x[n] {x[n]} = {. . . , 0, 1, 2, 3, 0, 0, . . . } 3 2 n h[n] {h[n]} = {. . . , 0, 1, 2, 0, . . . , 0. . . } 2 n Oct'04 CS 3291 28

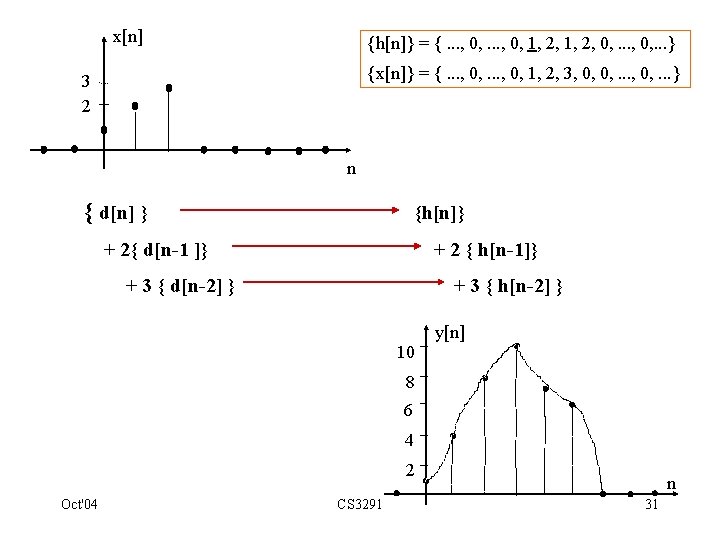
3. 17 Discrete time convolution graphically x[n] {h[n]} = {. . . , 0, 1, 2, 0, . . . } 3 2 {x[n]} = {. . . , 0, 1, 2, 3, 0, 0, . . . } h[n] n d[n] 2 n n 2 d[n-1] 2 h[n-1] 4 2 2 n n 3 d[n-2] 6 3 3 h[n-2] 3 n Oct'04 CS 3291 n 29

y[n] 10 8 6 4 2 n Express: {x[n]} = {d[n]} + 2 {d[n-1]} + 3 {d[n-2]} Response is: {y[n]} = {h[n]} + 2 {h[n-1} + 3 {h[n-2]} Oct'04 CS 3291 30

d[n] h[n] 2 n n 2 d[n-1] 2 h[n-1] 4 2 2 n n 3 d[n-2] 3 h[n-2] 6 3 3 n Oct'04 n CS 3291 32

3. 8. Stability: An LTI system is stable if its impulse-response {h[n]} satisfies: This means that {h[n]} must be either an FIR or an IIR whose samples decay towards zero as n . 3. 9. Causality: An LTI system operating in real time must be "causal " which means that its impulse-response {h[n]} must satisfy: h[n] = 0 for n < 0. Non-causal system would need “crystal ball ” to predict future. Oct'04 CS 3291 33

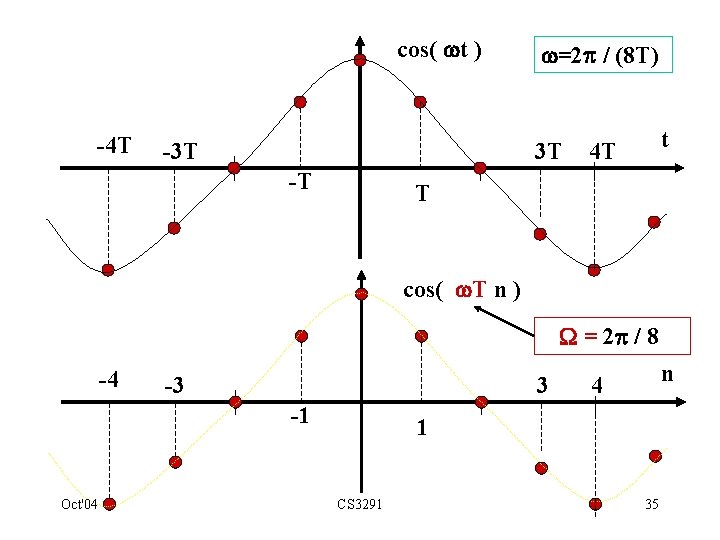
3. 10. Relative Frequency • Study effect of digital filters on sine-waves of different frequencies. • Discrete time sine-wave obtained by sampling A cos( t + ). • If sampling period is T seconds, resulting discrete time signal is : • = T is “ relative" frequency of sampled sine-wave. • Units of are 'radians per sample'. • To convert back to true frequency (radians/s ) multiply by 1/T. • Note: 1/T = sampling frequency, f S, in samples/second (Hz). ‘radians / sample’ times ‘samples / second’ = ‘radians / second’ • Normally process analogue signals in range 0 to f S /2 ( = 1/(2 T) ), • Restricts to the range 0 to . Oct'04 CS 3291 34

cos( t ) -4 T -3 T =2 / (8 T) 3 T -T t 4 T T cos( T n ) = 2 / 8 -4 -3 3 -1 Oct'04 n 4 1 CS 3291 35

Table gives values of & corresponding true frequencies : Relative frequency True frequency (radians/sample) (radians/s) (Hz) 0 0 /6 f. S/6 f. S/12 /4 f. S/4 fs/8 /3 f. S/3 fs/6 /2 f. S/2 fs/4 2 /3 2 f. S/3 fs/3 f. S/2 ‘radians / sample’ ‘samples / second’ = ‘radians / second’ Oct'04 CS 3291 36

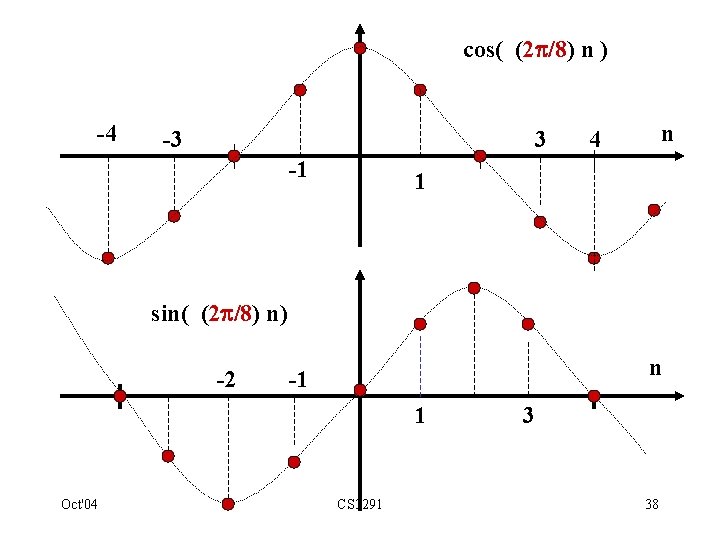
3. 11. Relative frequency response Response to sampled sine-waves calculated by defining: If this is applied to a system with impulse response {h[n]}, output would be {y[n]} with : Oct'04 CS 3291 37

cos( (2 /8) n ) -4 -3 3 -1 n 4 1 sin( (2 /8) n) -2 n -1 1 Oct'04 CS 3291 3 38

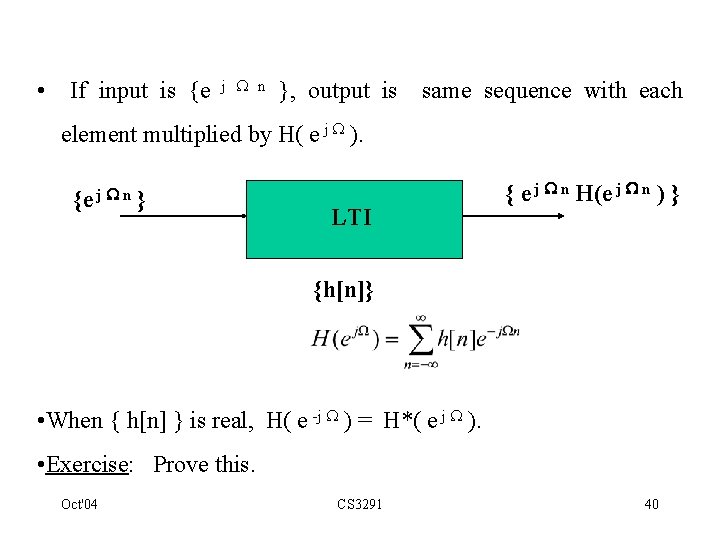
• H( e j ) is the " relative frequency response " of LTI system. • Complex number for any value of . • It is DTFT of { h[n] }. • Note similarity to the analogue Fourier transform. Oct'04 CS 3291 39

• If input is {e j n }, output is same sequence with each element multiplied by H( e j ). {e j n } LTI { e j n H(e j n ) } {h[n]} • When { h[n] } is real, H( e -j ) = H*( e j ). • Exercise: Prove this. Oct'04 CS 3291 40

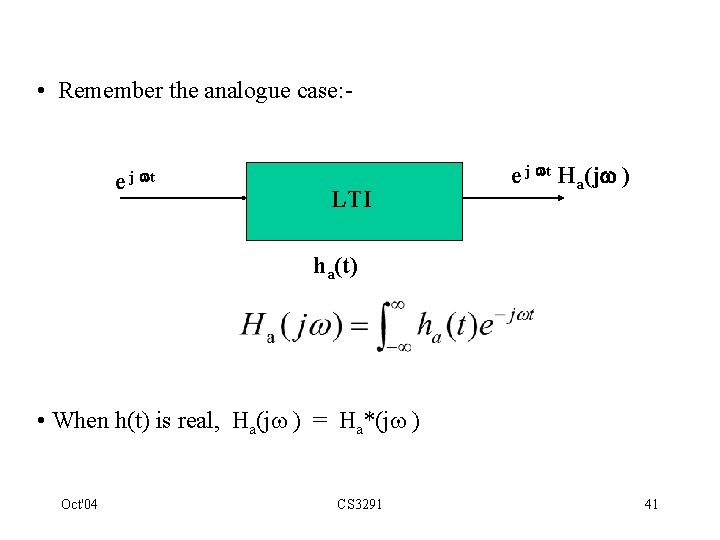
• Remember the analogue case: - e j t LTI e j t Ha(j ) ha(t) • When h(t) is real, Ha(j ) = Ha*(j ) Oct'04 CS 3291 41

3. 12. Gain and phase responses • Expressing H( e j ) = G( ) e j ( ) • G( ) = |H( e j )| is "gain ” • ( ) = arg ( H( e j ) ) is "phase lead”. • Both vary with . • If input is {A cos( n)}, • output is: { G( )A cos( n + ( )) } Exercise: Prove this • When input is sampled sine-wave of rel frequency , output is sine-wave of same frequency , but with amplitude scaled by G( ) & phase increased by ( ). Oct'04 CS 3291 42

Gain & phase response graphs again - ( ) 20 log 10[G( )] d. B - ( ) G( ) in d. B 0 Oct'04 /2 3 /4 CS 3291 43

• Common to plot graphs of G( ) & ( ) against . • G( ) often converted to d. Bs by calculating 20 log 10( G( ) ). • Restrict to lie in range 0 to & adopt a linear horizontal scale. • Example 3. 2: Calculate gain & phase response of FIR digital filter in Figure 3. 3 where A 1 = 1, A 2 = 2, A 3 = 3, A 4 = -4, A 5 = 5. • Solution: Impulse response is: {. . , 0, 1, 2, 3, -4, 5 , 0, . . }. By the formula established above, H( e j ) = 1 + 2 e - j + 3 e -2 j - 4 e -3 j + 5 e - 4 j To obtain the gain and phase at any take modulus and phase. Best done by computer, either by writing & running a simple program, or by running a standard package. A simple program is given at the end of these notes. Oct'04 CS 3291 44

• Can use a spread-sheet such as excel (see lecture notes) • Another way of calculating gain & phase responses for H( e j ) = 1 + 2 e - j + 3 e -2 j - 4 e -3 j + 5 e - 4 j is to start MATLAB and type: A = [ 1 2 3 -4 5 ]; freqz( A ); • See later section 3. 18 for graphs produced. Oct'04 CS 3291 45

• Produces graphs of gain & phase responses of H( ej ). • Frequency scale normalised to f. S/2 & labelled 0 to 1 instead of 0 to . • See Section 3. 18 • In next section we calculate coeffs of an FIR filter to achieve a particular type of gain & phase response. • To calculate gain & phase responses for an IIR filter would be difficult by method used above because impulse-response has infinite number of non-zero terms. • There is an easier method in a later section. Oct'04 CS 3291 46

Phase delay • Assume input is {A cos( n)}, • Output is: { G( ) A cos ( n + ( ) ) } = { G( ) A cos ( [ n + ( ) / ] ) } = { G( ) A cos ( [ n - (- ( ) / ) ] ) } • Phase lead ( ) delays sine-wave by - ( )/ sampling intervals • This is ‘phase-delay’. Oct'04 CS 3291 47

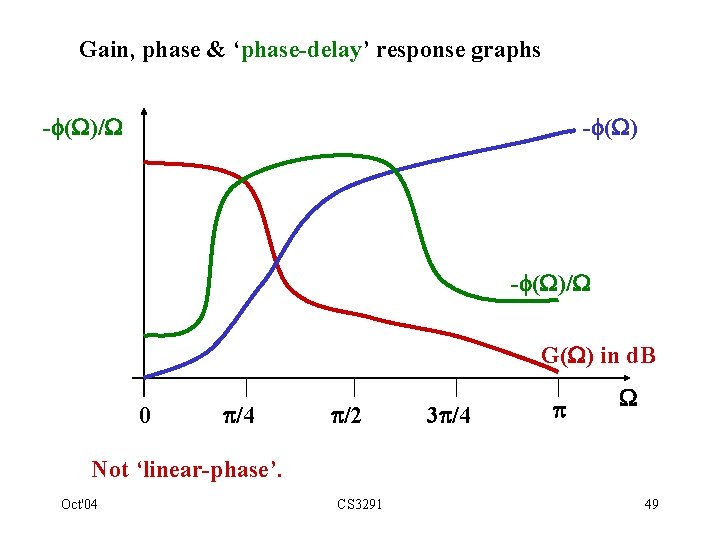
3. 13. Linear phase response • If - ( )/ remains constant for all values of , i. e. if - ( ) = k for constant k, system has ‘linear phase’ response. • Graph of - ( ) against on linear scale would then be straight line with slope k where k is "phase delay" i. e. the delay measured in sampling intervals. • This need not be an integer. Oct'04 CS 3291 48

Gain, phase & ‘phase-delay’ response graphs - ( )/ G( ) in d. B 0 /4 /2 3 /4 Not ‘linear-phase’. Oct'04 CS 3291 49

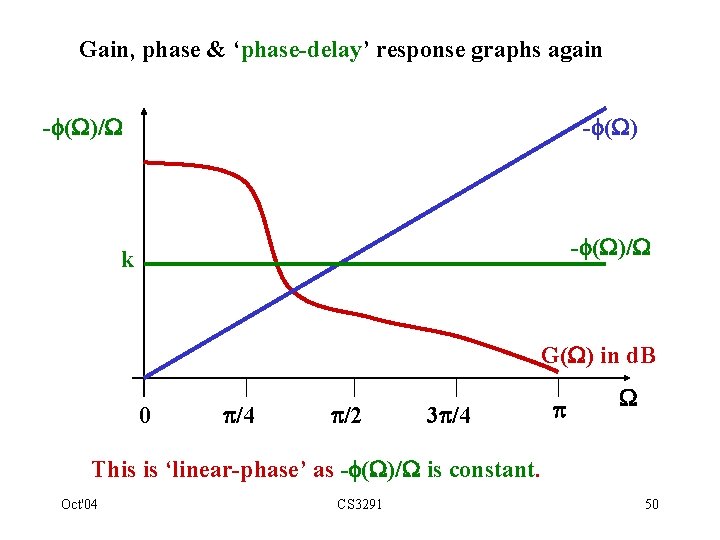
Gain, phase & ‘phase-delay’ response graphs again - ( )/ k G( ) in d. B 0 /4 /2 3 /4 This is ‘linear-phase’ as - ( )/ is constant. Oct'04 CS 3291 50

• Linear phase systems of special interest since all sine-waves are delayed by same number of sampling intervals. • Input signal expressed as Fourier series will have all its sinusoidal components delayed by same amount of time. • In absence of amplitude changes, output signal will be exact replica of input. • LTI systems are not necessarily linear phase. • A certain class of digital filter can be made linear phase. Oct'04 CS 3291 51

3. 14. Inverse DTFT • Frequency -response H( e j ) is DTFT of {h[n]}. • Inverse DTFT formula allows {h[n]} to be deduced from H(e j ) : • Observe similarities with analogue Fourier transform: (i) (1/2 ) factor, (ii) sign of j n (n replaces t). (iii) variable of integration (d ) Oct'04 CS 3291 52

Also note that with DTFT: • Negative frequencies are again included. • Range of integration is now - to rather than - to . • Forward transform is a summation & inverse transform is an integral. • This is because {h[n]} is a sequence whereas H(e j ) is function of the continuous variable . Oct'04 CS 3291 53

3. 15 Problems: 1. Show that y[n]=(x[n]) 2 is not LTI. 2. If {h[n]}= {. . 0, . . , 0, 1, -1, 0, . . }, calculate response to {x[n]} = {. . 0, . . , 0, 1, 2, 3, 4, 0, . . . }. 3. . Produce a signal flow graph for each of the following difference equations: (i) y[n] = x[n] + x[n-1] (ii) y[n] = x[n] - y[n-1] 4. For each difference equation in question 3, determine the impulse response, & deduce whether the system it represents is stable and/or causal. . 5. Calculate, by tabulation, the output from difference equation (ii) in question 3 when the input is the impulse response of difference equation (i). 6. If f. S =8000 Hz, what true frequency corresponds to /5 radians/sample? 7. Sketch the gain & phase responses of the system referred to in question 2. (You don't need a computer program. ) Is it a linear phase system? 8. Calculate the impulse response for y[n] = 4 x[n] - 2 y[n-1]. Is it stable? 9. Show that input {cos( n)} produces an output {G( )cos( n+ ( ))}. 10. For y[n]=x[n]+2 x[n-1]+3 x[n-2]+2 x[n-3]+x[n-4], sketch phase response and comment on its significance. Show that ( ) = -2. Oct'04 CS 3291 54

3. 16. Progam for gain & phase responses of FIR digital filter. (using complex arithmetic) fs = input('enter fs: '); M = input('Enter order: '); disp('Enter coefficients: '); for N = 0: M C(N+1)=input('coeff = '); end; disp(' FREQ(Hz) GAIN(d. B. ) PHASE LEAD(deg)'); K = 0; F =0. 0; % F is frequency in Hz} while F < fs/2 H=0; W =2*pi*F/fs; for N=0: M H=H+C(N+1)*exp(-j*W*N); end; MD=abs(H); PH = angle(H); GAIN(K+1)=-999; if MD>0 GAIN(K+1)=20*log 10(MD); end; PHAS(K+1)=PH*180. 0/pi; disp([num 2 str(F) ' 'num 2 str(GAIN(K+1)) ' F=F+fs/200; K=K+1; 'num 2 str(PHAS(K+1))]); end; %while loop Oct'04 CS 3291 55

3. 16. Progam for gain & phase responses of FIR digital filter. (without complex arithmetic) fs = input('enter fs: '); M = input('Enter order: '); disp('Enter coefficients: '); for N = 0: M H(N+1)=input('coeff = '); end; disp(' FREQ(Hz) GAIN(d. B. ) PHASE LEAD(deg)'); K = 0; F =0. 0; % F is frequency in Hz} while F < fs/2 Hre =0. 0; Him =0. 0; W =2*pi*F/fs; for N=0: M Hre=Hre+H(N+1)*cos(W*N); Him=Him-H(N+1)*sin(W*N); end; MD=sqrt(Hre*Hre+Him*Him); PH = atan 2(Him, Hre); GAIN(K+1)=-999; if MD>0 GAIN(K+1)=20*log 10(MD); end; PHAS(K+1)=PH*180. 0/pi; disp([num 2 str(F) ' 'num 2 str(GAIN(K+1)) ' 'num 2 str(PHAS(K+1))]); F=F+fs/200; K=K+1; end; %while loop Oct'04 CS 3291 56

Sample run: FIR FREQUENCY RESPONSE Enter sampling frequency(Hz): 1000 Enter order of FIR filter: 3 Enter coefficients: H[0] = 1 H[1] = 2 H[2] = 1 H[3] = 2 Output obtained: - Freq(Hz) Gain(DB) Phase(deg) 0 15. 56 0. 0 5 15. 56 -3. 0 15. 56 -6. 0 : : : 500 6. 01 -180. 0 } Oct'04 CS 3291 57

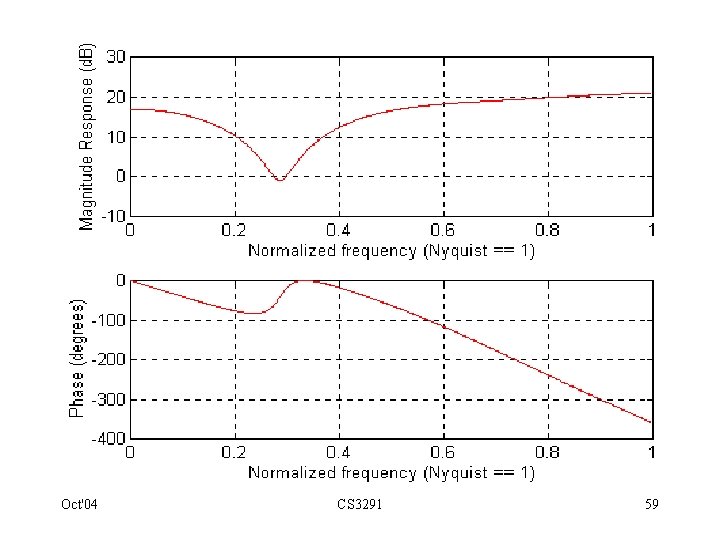
3. 18. Frequency response of FIR digital filter by MATLAB • Given discrete time LTI system with difference equation: y[n] = x[n] + 2 x[n-1] + 3 x[n-2] - 4 x[n-3] + 5 x[n-4] • Its impulse response is: {. . . , 0, 1 , 2, 3, -4, 5, 0, . . . } • Its frequency response is: H( e j ) = 1 + 2 e - j + 3 e -2 j - 4 e -3 j + 5 e - 4 j • To calculate its gain and phase responses, type: freqz ( [ 1 2 3 -4 5 ]) ; • Resulting graphs have a normalised frequency scale with “ 1” corresponding to = radians/sample; i. e. one half of the sampling frequency. Oct'04 CS 3291 58

Oct'04 CS 3291 59