CS 3240 Chapter 3 Regular Languages and Grammars

CS 3240 – Chapter 3 Regular Languages and Grammars

Directory Operations How would you delete all C++ files from a directory from the command line? How about all Power. Point files that start with the letter a? Power. Point file names that contain the string 3240? CS 3240 - Regular Languages and Grammars 2

Patterns for Strings *. cpp a*. ppt *3240*. ppt These are wildcard expressions Not bona fide regular expressions CS 3240 - Regular Languages and Grammars 3

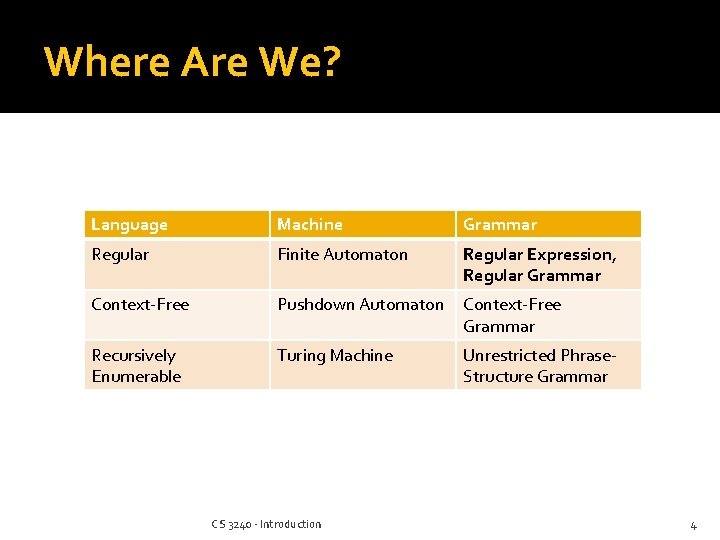
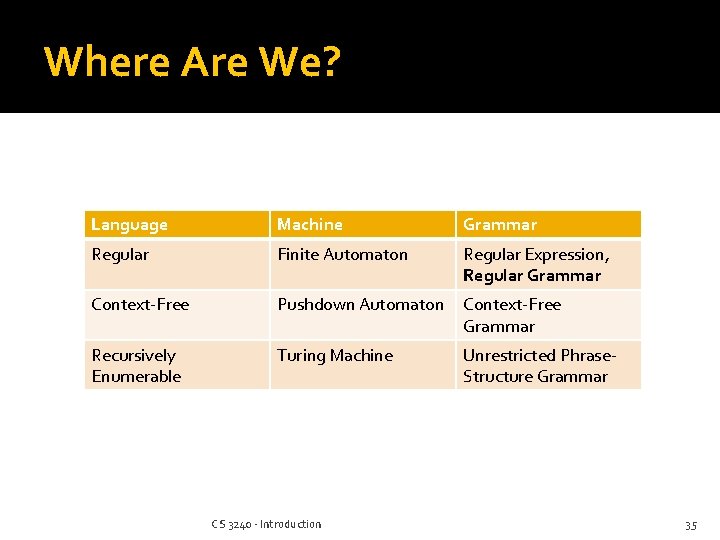
Where Are We? Language Machine Grammar Regular Finite Automaton Regular Expression, Regular Grammar Context-Free Pushdown Automaton Context-Free Grammar Recursively Enumerable Turing Machine Unrestricted Phrase. Structure Grammar CS 3240 - Introduction 4

Regular Expressions Text patterns that represent regular languages We’ll show shortly that for every regular expression there is a finite automaton that accepts that language And vice-versa The operators are: () (Grouping) * + xy (Kleene Star) (Union) (Concatenation) CS 3240 - Regular Languages and Grammars 5

Recursive Definitions of Sets 1) Specify base case(s) 2) Show to generate other elements Rules that use what’s in the set already Example: Non-negative multiples of 5, F 1) 0, 5 is in F 2) For x, y in F, then x + y is in F Alternate definition: 1) 0 is in F 2) For x in F, so is x + 5 CS 3240 - Regular Languages and Grammars 6

Regular Expressions Recursive Definition Base cases: The empty set: ∅ or ( ) The empty string: λ Any letter in Σ Recursive rules: Given regular expressions r, r 1, r 2: (r) r* r 1 + r 2 r 1 r 2 (Grouping) (Kleene Star) (Union) (Concatenation) CS 3240 - Regular Languages and Grammars 7

Regular Expressions Examples All strings beginning with a: a(a + b)* All strings containing aba: (a + b)*aba(a + b)* All strings of even length: ((a + b))* = (aa + ba + ab + bb)* = ((a + b)2)* All strings of odd length: (a+b)((a + b)2)* Valid decimal integers in C: (1+2+3+4+5+6+7+8+9)(0+1+2+3+4+5+6+7+8+9)* CS 3240 - Regular Languages and Grammars 8

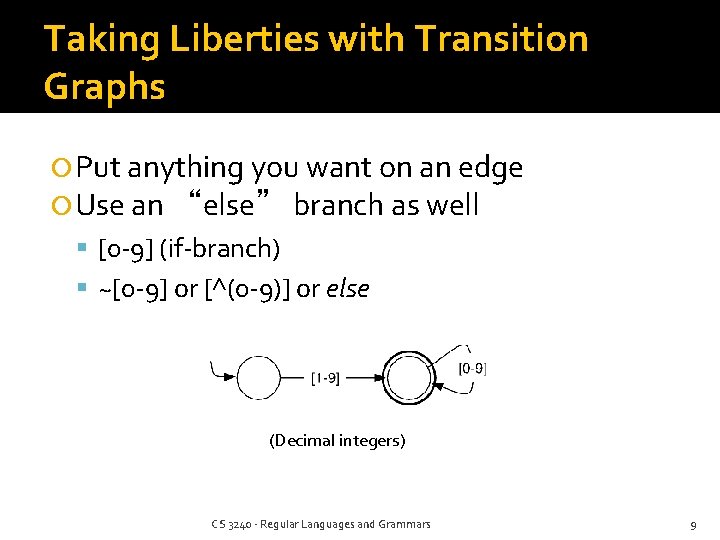
Taking Liberties with Transition Graphs Put anything you want on an edge Use an “else” branch as well [0 -9] (if-branch) ~[0 -9] or [^(0 -9)] or else (Decimal integers) CS 3240 - Regular Languages and Grammars 9

What Language? (b*ab*ab*ab* + b) * = b* (ab*ab*ab*) * = b* + (b*ab*ab*ab*) * (a(a+bb) *) * ((a + b)a) * CS 3240 - Regular Languages and Grammars 10

Language Associated with a Regular Expression (Stating the Obvious) L(∅) =∅ L(λ) = λ L(c) = c, for c ∊ Σ L((r)) = L(r) L(r*) = L(r)* L(r 1 + r 2) = L(r 1) ∪ L(r 2) L(r 1 r 2) = L(r 1)L(r 2) CS 3240 - Regular Languages and Grammars 11

“Algebra” of Regular Expressions r+s = s+r (r+s)+t = r+(s+t) r+r = r r + ∅ = r (rs)t = r(st) rλ = λr = r r ∅ = ∅r = ∅ r(s+t) = rs+rt (r+s)t = rt+st CS 3240 - Regular Languages and Grammars 12

Regular Expressions and Finite Automata (Section 3. 2) 1. For every regular expression there is an associated NFA that accepts the same language And therefore a DFA, by conversion 2. For every FA (either NFA or DFA) there is a regular expression that represents the same language CS 3240 - Regular Languages and Grammars 13

Regular Expression => NFA We will show to convert each element of the definition of regular expressions to an NFA This is sufficient! And shows the convenience of recursive definitions (review slide 7 now) because if we can give a machine for every case in the definition of REs, we are done! CS 3240 - Regular Languages and Grammars 14

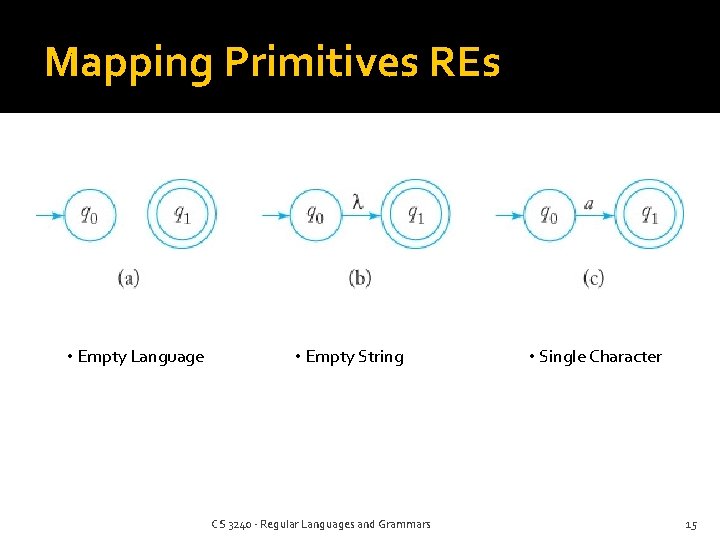
Mapping Primitives REs • Empty Language • Empty String CS 3240 - Regular Languages and Grammars • Single Character 15

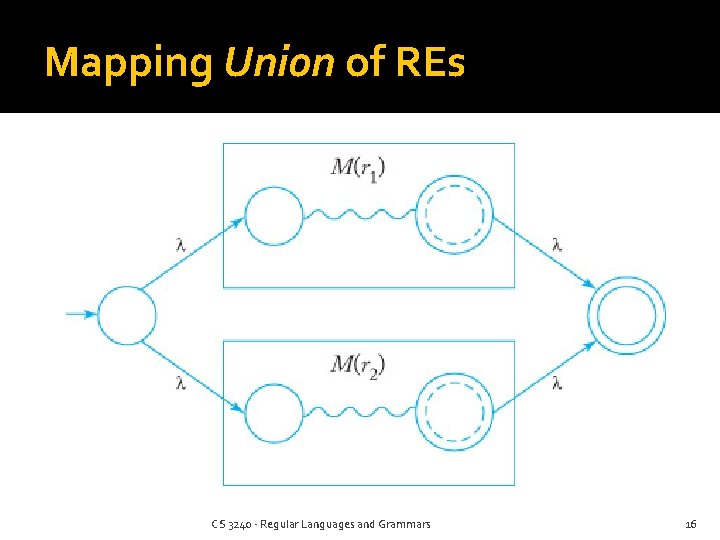
Mapping Union of REs CS 3240 - Regular Languages and Grammars 16

Mapping Union of REs A Simplification Just draw the lambdas from a new start state to the start states of each machine Remove the start notation from the original start states (No need to have a new final state) CS 3240 - Regular Languages and Grammars 17

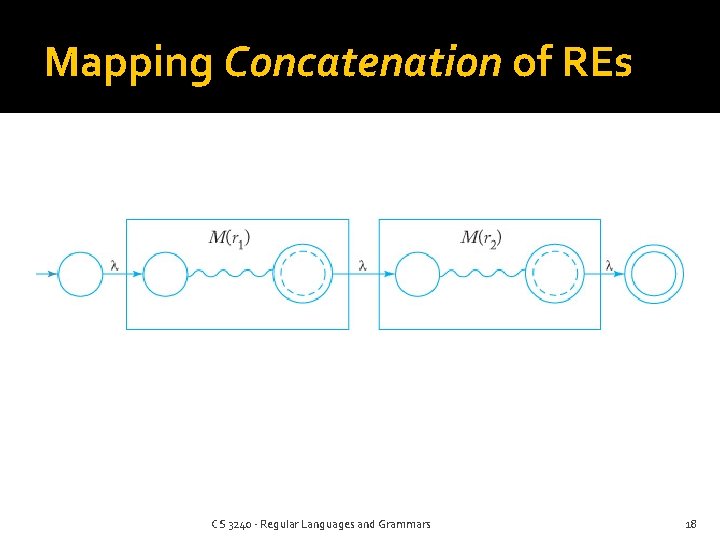
Mapping Concatenation of REs CS 3240 - Regular Languages and Grammars 18

Mapping Concatenation of REs A Simplification 1) Just draw a lambda from each final state of the first machine to the start state of the second machine 2) remove the acceptability of those final states of the first machine CS 3240 - Regular Languages and Grammars 19

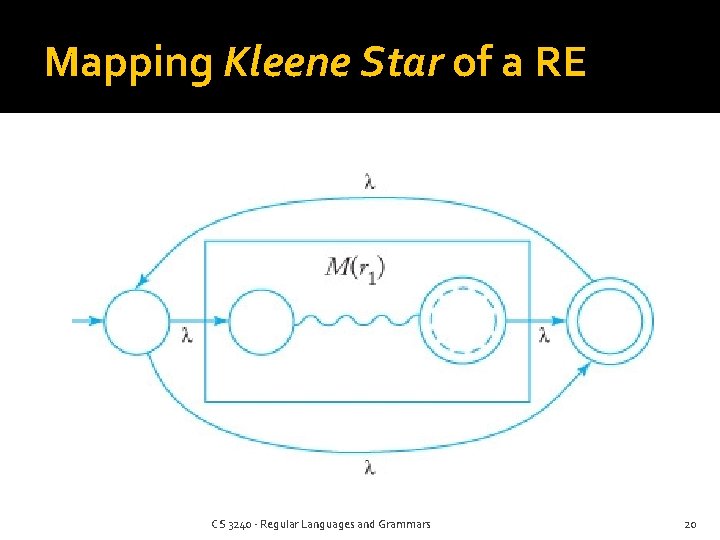
Mapping Kleene Star of a RE CS 3240 - Regular Languages and Grammars 20

Mapping Kleene Star of a RE A Simplification We need to do two things: 1) Add the empty string, if needed 2) Loop from each final state back to the start state Procedure: 1) If the empty string is not accepted, create a new start state which accepts, and connect to the original start state with λ 2) Add a λ-edge from each final state to the original (or the new) start state CS 3240 - Regular Languages and Grammars 21

Practice Draw NFAs for the REs on slides 8 and 9 CS 3240 - Regular Languages and Grammars 22

FA => Regular Expression First remove all jails Then, if needed, convert the DFA to an equivalent NFA with A start state with no incoming edges A single final state with no outgoing edges Will need lambda transitions for this Then “eliminate” all but the start and final states Without changing the language accepted Using GTGs… CS 3240 - Regular Languages and Grammars 23

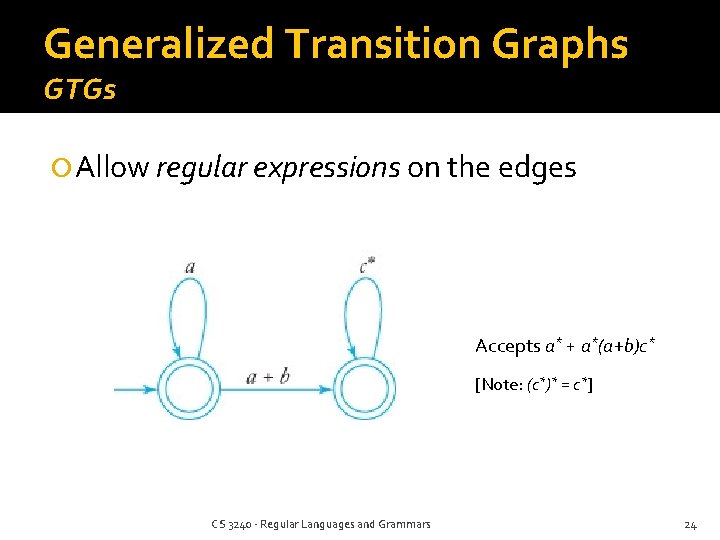
Generalized Transition Graphs GTGs Allow regular expressions on the edges Accepts a* + a*(a+b)c* [Note: (c*)* = c*] CS 3240 - Regular Languages and Grammars 24

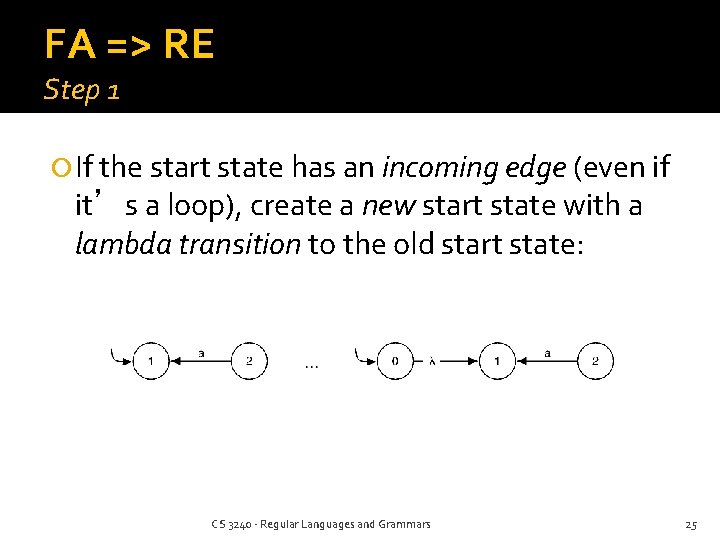
FA => RE Step 1 If the start state has an incoming edge (even if it’s a loop), create a new start state with a lambda transition to the old start state: CS 3240 - Regular Languages and Grammars 25

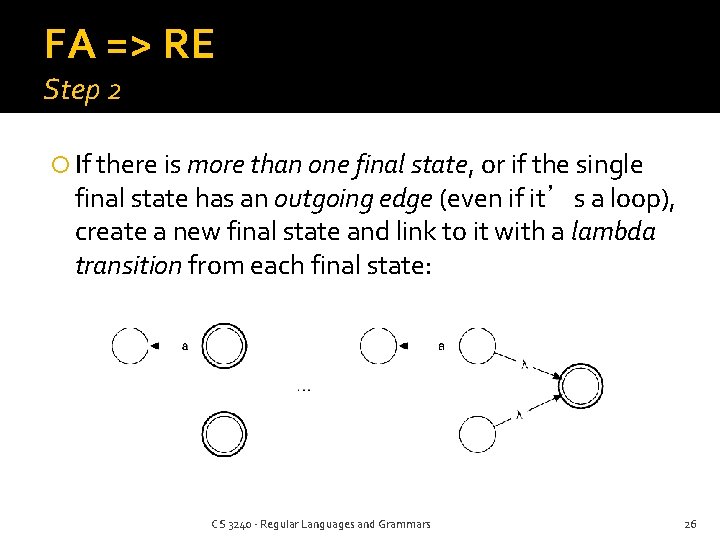
FA => RE Step 2 If there is more than one final state, or if the single final state has an outgoing edge (even if it’s a loop), create a new final state and link to it with a lambda transition from each final state: CS 3240 - Regular Languages and Grammars 26

FA => RE Step 3 “Remove” each intermediate state, one at a time: 1. Combine each incoming path with each outgoing path (only “through” paths; not loops) 2. Determine the regular expression equivalent to the combined path through the current state 3. Add an edge with that RE between the incoming state and the outgoing state 4. Repeat until all intermediate states vanish CS 3240 - Regular Languages and Grammars 27

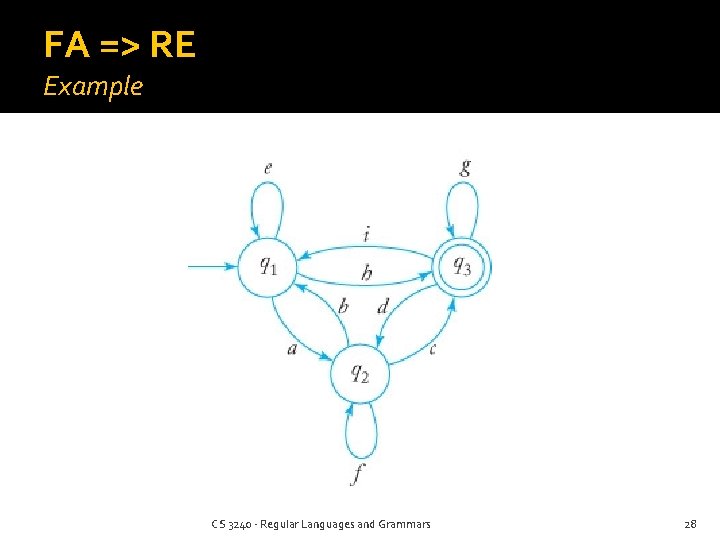
FA => RE Example CS 3240 - Regular Languages and Grammars 28

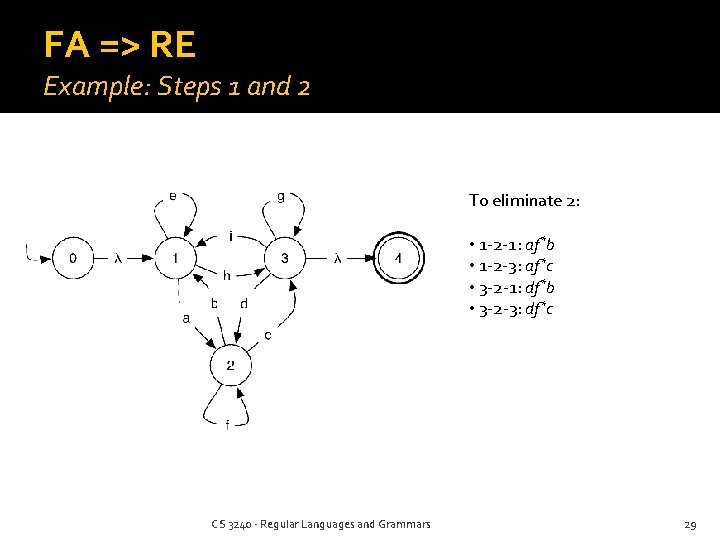
FA => RE Example: Steps 1 and 2 To eliminate 2: • 1 -2 -1: af*b • 1 -2 -3: af*c • 3 -2 -1: df*b • 3 -2 -3: df*c CS 3240 - Regular Languages and Grammars 29

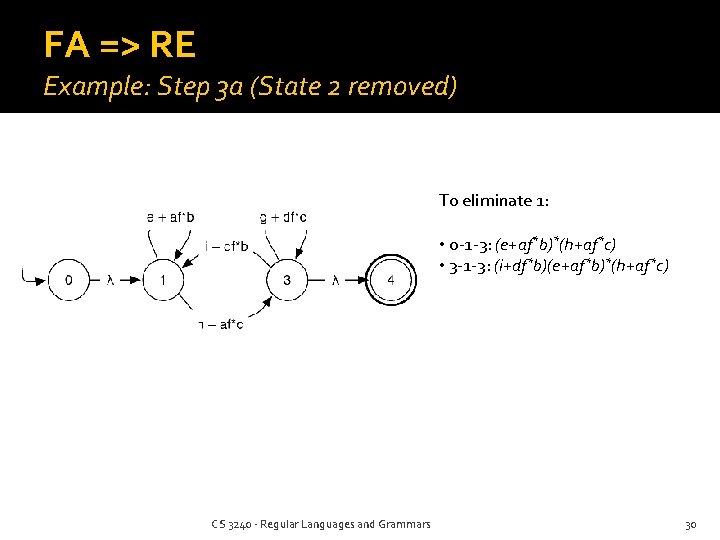
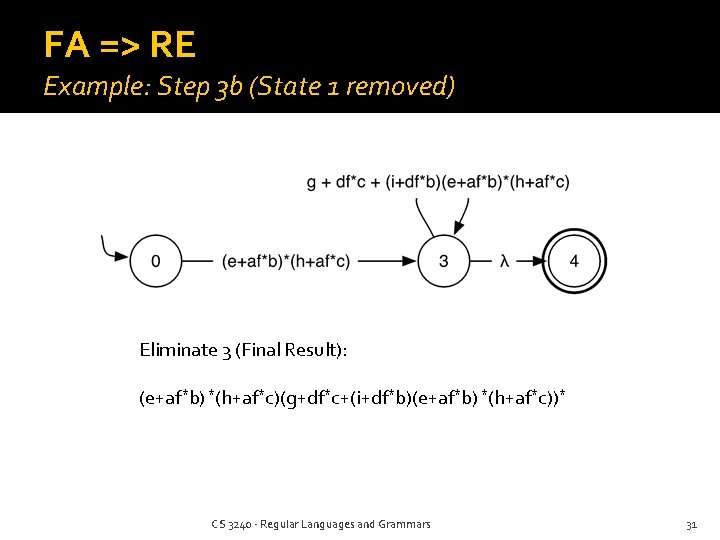
FA => RE Example: Step 3 a (State 2 removed) To eliminate 1: • 0 -1 -3: (e+af*b)*(h+af*c) • 3 -1 -3: (i+df*b)(e+af*b)*(h+af*c) CS 3240 - Regular Languages and Grammars 30

FA => RE Example: Step 3 b (State 1 removed) Eliminate 3 (Final Result): (e+af*b) *(h+af*c)(g+df*c+(i+df*b)(e+af*b) *(h+af*c))* CS 3240 - Regular Languages and Grammars 31

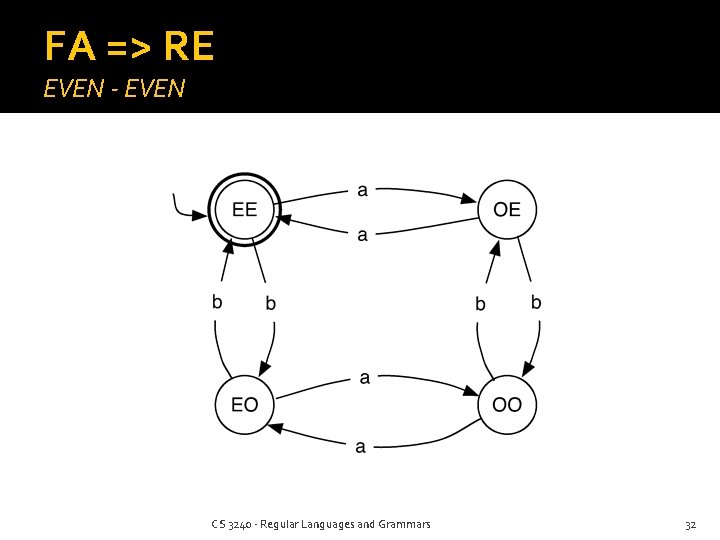
FA => RE EVEN - EVEN CS 3240 - Regular Languages and Grammars 32

Exercise Find a regular expression for the language containing all strings that do not contain the substring aa CS 3240 - Regular Languages and Grammars 33

FA => RE Online Document See bypass. doc Shows different possibilities by eliminating states in different orders But the REs obtained are equivalent ▪ Meaning they represent the same language CS 3240 - Regular Languages and Grammars 34

Where Are We? Language Machine Grammar Regular Finite Automaton Regular Expression, Regular Grammar Context-Free Pushdown Automaton Context-Free Grammar Recursively Enumerable Turing Machine Unrestricted Phrase. Structure Grammar CS 3240 - Introduction 35

Regular Grammars Section 3. 3 There is a natural correspondence between FAs and grammars Right-linear Grammars “Linear” means there is at most one variable on the right-hand side of the rule “Right-linear” means the variable occurs as the last entry in the rule: ▪ A → ab. C CS 3240 - Regular Languages and Grammars 36

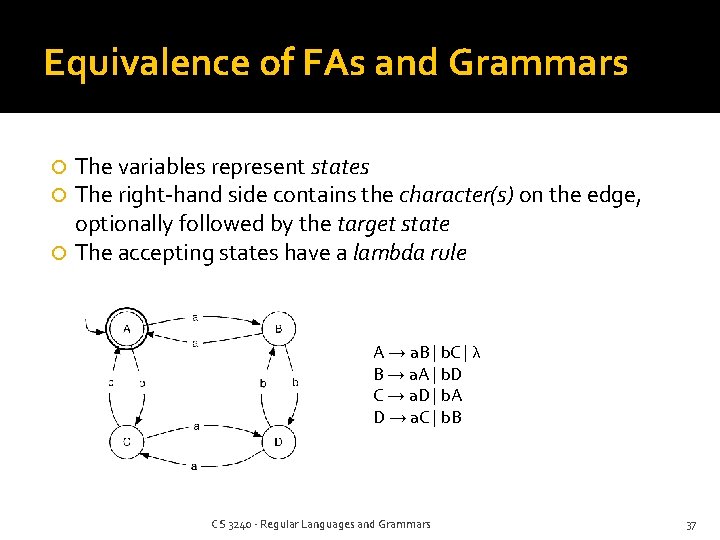
Equivalence of FAs and Grammars The variables represent states The right-hand side contains the character(s) on the edge, optionally followed by the target state The accepting states have a lambda rule A → a. B | b. C | λ B → a. A | b. D C → a. D | b. A D → a. C | b. B CS 3240 - Regular Languages and Grammars 37

Rules Without a Variable Go to an accepting state with no out-edges A→b CS 3240 - Regular Languages and Grammars 38

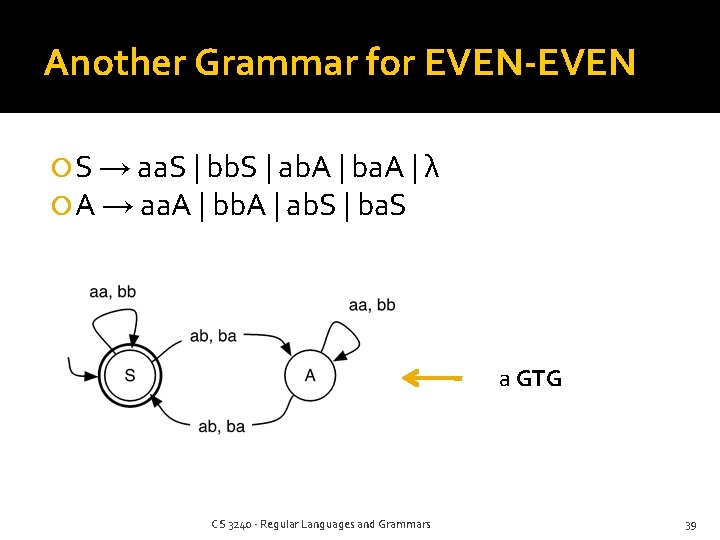
Another Grammar for EVEN-EVEN S → aa. S | bb. S | ab. A | ba. A | λ A → aa. A | bb. A | ab. S | ba. S a GTG CS 3240 - Regular Languages and Grammars 39

Exercise Construct a regular grammar for the language denoted by aab*a 1. First build a GTG 2. Then map to a right-linear grammar CS 3240 - Regular Languages and Grammars 40

A Left-Linear Grammar aab*a S → Xa X → Xb | aa How did I come up with this? CS 3240 - Regular Languages and Grammars 41

Left-linear = Right-linear If you have the single variable only at the left ends, you have a left-linear grammar This is also a regular grammar We will show to convert between rightlinear and left-linear grammars We will use two facts to establish the process: If L is regular, so is LR (Section 2. 3, exercise 12) L(GR) = L(G)R (obvious, but on next slide…) CS 3240 - Regular Languages and Grammars 42

R L(G ) = R L(G) GR means you reverse the right-hand sides of each rule in a grammar, G The language generated is L(G)R (the reverse of L(G)) S → ab. S | X X → b. X | λ S → Sba | X X → Xb | λ (ab)*b* b*(ba)* CS 3240 - Regular Languages and Grammars 43

Convert Right-linear to Left-linear Using 2 Reversals Convert the right-linear grammar to a GTG 2. “Reverse” the GTG (a la Section 2. 3, #12) 1. Ensure a single final state (use λ if needed) Interchange the role of the start and final states Reverse all arrows Convert the reversed GTG to a right-linear grammar 4. Reverse the right-hand sides of each rule to obtain the left-linear grammar 3. CS 3240 - Regular Languages and Grammars 44

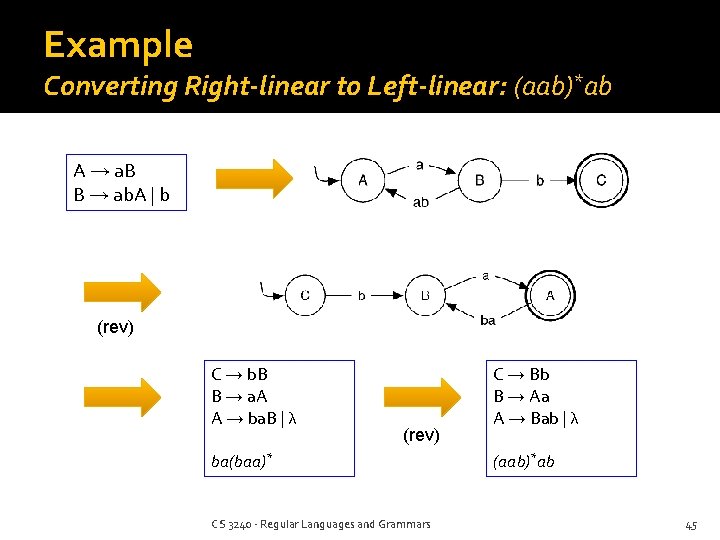
Example Converting Right-linear to Left-linear: (aab)*ab A → a. B B → ab. A | b (rev) C → b. B B → a. A A → ba. B | λ (rev) ba(baa)* CS 3240 - Regular Languages and Grammars C → Bb B → Aa A → Bab | λ (aab)*ab 45

Convert Left-linear to Right-linear Reverse the Steps on Previous Slide Reverse the grammar, G, obtaining right- linear grammar, GR, for L(G)R Convert to GTG Reverse the GTG Convert to Right-linear CS 3240 - Regular Languages and Grammars 46

Summary CS 3240 - Regular Languages and Grammars 47