CS 321 Programming Languages and Compilers Lectures 16

CS 321 Programming Languages and Compilers Lectures 16 & 17 Introduction to Formal Languages Regular Languages Lexical Analysis Finite Automata & Lexing

Languages • Have a finite vocabulary • Have finite length sentences • Have possibly infinitely many sentences 2 Finite Automata & Lexing

Grammars and Recognizers • A Grammar is a finitary method by which all sentences of a language, L, may be generated via well-defined rules. • A Recognizer is a procedure which, given a “string” x, answers “yes” if x L • We usually also want to answer “no” if x L, I. e. usually demand an algorithm. ) 3 Finite Automata & Lexing

(Context-Free) Grammars • Def. A (context-free or Chomsky Type-2) grammar (cfg) is a 4 -tuple G = (N, , P, S) where – N is a finite, non-empty set of symbols (non-terminal vocabulary) – is a finite set of symbols (terminal vocabulary) – N = – V N (vocabulary) – S N (goal symbol) – P is a finite subset of N V* (production rules) 4 Finite Automata & Lexing

Set Operations • Def. Let X and Y be sets of words XY {xy | x X and y Y} X 0 { } (where represents the empty string) X 1 X XI+1 Xi. X X* i 0 X i X+ i > 0 Xi (so X+ = X* X) 5 Finite Automata & Lexing

Example • G = (N, , P, E) where N = {E, T, F} = {[, ], +, *, id} P = {(E, T), (E, E+T), (T, F), (T, T*F), (F, id), (F, [E])} • (so V = N = {E, T, F, [, ], +, *, id}) • (A, ) P is usually written A or A : : = or A : 6 Finite Automata & Lexing

Convention • Given G = (N, , P, S) (with V = N ) (or G = (V, , P, S) with N=V- ) – – – elements of N: A, B, … elements of V: … U, V, W, X, Y, Z elements of : a, b, … elements of *: … u, v, w, x, y, z elements of V *: , , , • others: – – – names (not underlined) : N S: N underlined or courier font: special symbols: is used to denote a production rule: ( = A ) 7 Finite Automata & Lexing

Generating L • How to use a grammar, G, to generate a sentence in L(G): • Begin with a string, consisting of only the goal symbol. • repeat select from a non-terminal “A” and “rewrite” A according to some production (A, ) thereby producing ’ from . until ’ * 8 Finite Automata & Lexing

Example G = (N, , P, S) where P is (abbreviated) as follows: E T|E+T T F|T*F F id | < E > and where N = {E, T, F, Q} = {+, *, <, >, id} S=E 9 Finite Automata & Lexing

Regular Sets • Regular sets (also called regular languages) are defined as follows. Let be a finite alphabet. 1) is a regular set over . 2) { } is a regular set over . 3) a , {a} is a regular set over . 4) If P and Q are regular sets over , a) P Q is a regular set over . b) PQ is a regular set over . c) P* is a regular set over . 5) Nothing else is a regular set over . 10 Finite Automata & Lexing

Regular Expressions 1) denotes the regular set . 2) denotes the regular set { }. 3) a denotes the regular set {a}. 4) If p and q are regular expressions denoting the regular sets P and Q respectively, then a) (p|q) denotes P Q. b) (pq) denotes PQ. c) (p)* denotes p* 5) Nothing else is a regular expression. *** Notation: (p)+ ((p)*p) (p)? p | 11 Finite Automata & Lexing

Right-Linear Grammars (Generators for Regular Sets) • Def. Let G = (N, , P, S) be a cfg. G is said to be right-linear if P N ( * *N) *** • Proposition. If G is a right-linear cfg then L(G) is a regular set over . • Proposition. If R is a regular set over , then a right-linear cfg, G, for which L(G) = R. 12 Finite Automata & Lexing

Finite Automata (Recognizers for Regular Sets Def. A deterministic finite automaton (deterministic finite state machine) is a 5 -tuple: M = (Q, , , q 0, F) where 1) Q is a finite non-empty set of states. 2) is a finite set of input symbols. 3) q 0 Q (initial state) 4) F Q (final states) 5) is a partial mapping from Q to Q (transition function or move function) 13 Finite Automata & Lexing

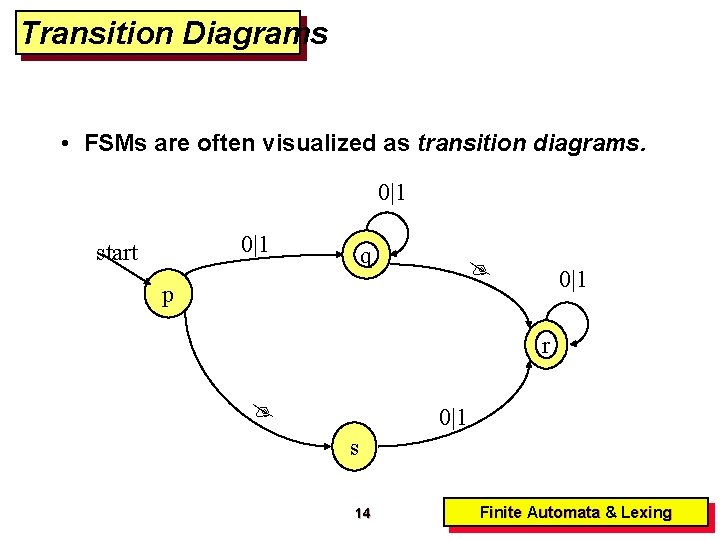
Transition Diagrams • FSMs are often visualized as transition diagrams. 0|1 start q 0|1 p r 0|1 s 14 Finite Automata & Lexing

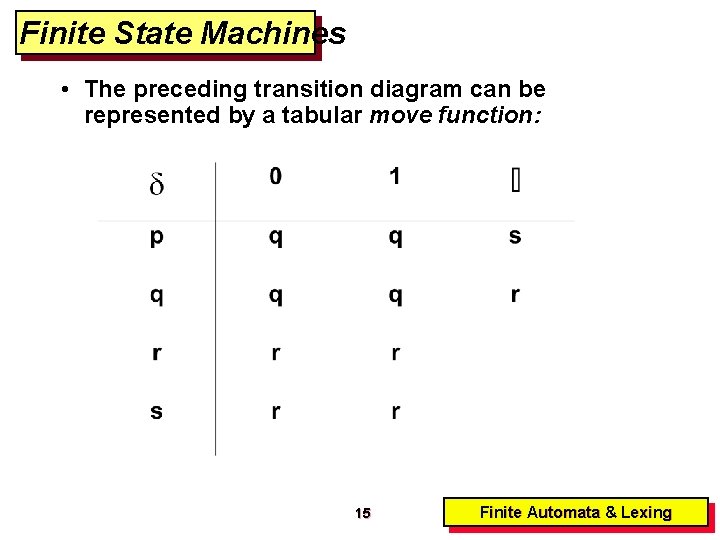
Finite State Machines • The preceding transition diagram can be represented by a tabular move function: 15 Finite Automata & Lexing

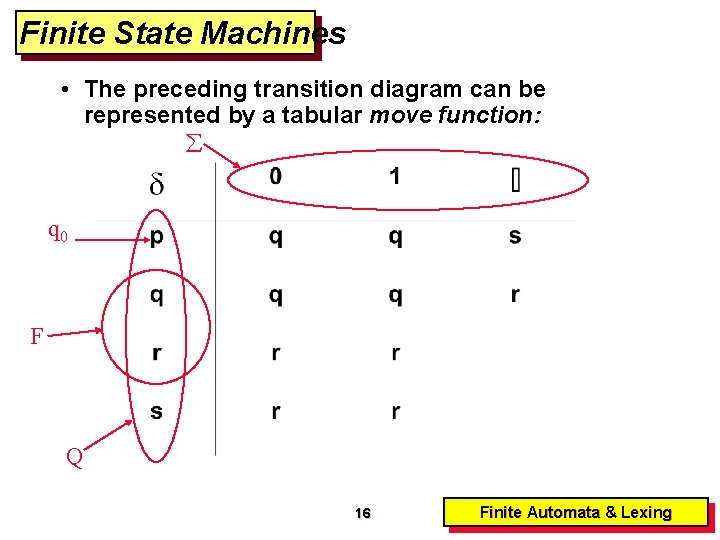
Finite State Machines • The preceding transition diagram can be represented by a tabular move function: q 0 F Q 16 Finite Automata & Lexing

Formalizing the Moves of a FSM • A pair (q, u) in Q * is called a configuration of M. • (q 0, u) is an initial configuration. • M proceeds from one configuration to the next by moving according to the transition function: (q, au) (q’, u) if (q, a)=q’ (q, u) … (q’, v) is written (q, u) * (q’, v) • The language accepted (or defined) by M is L(M) = {u * | (q 0, u) * (q, ) for some q F} Note: Sometimes is used to denote the empty string 17 Finite Automata & Lexing

Example • With the machine M = ({p, q, r, s}, {0, 1, }, , p, {q, r}) where the move function is shown in the preceding table. • Question 1: Is 01 0 L(M)? • Question 2: Is L(M)? • Question 3: Is 0 1 0 L(M)? 18 Finite Automata & Lexing

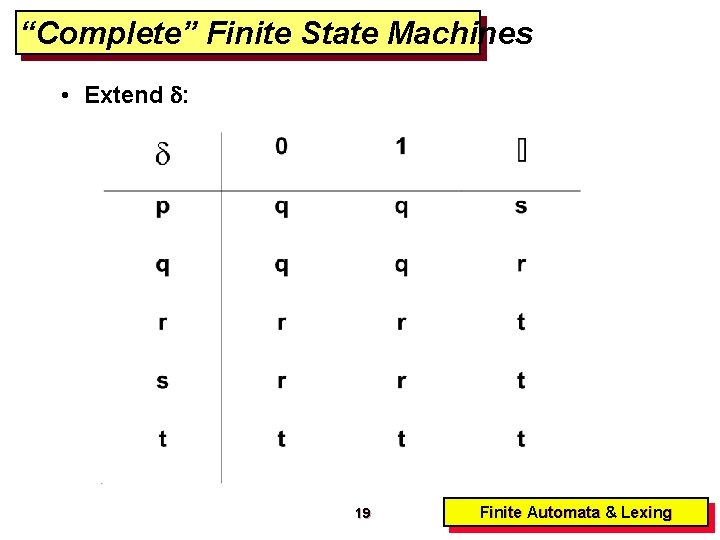
“Complete” Finite State Machines • Extend : 19 Finite Automata & Lexing

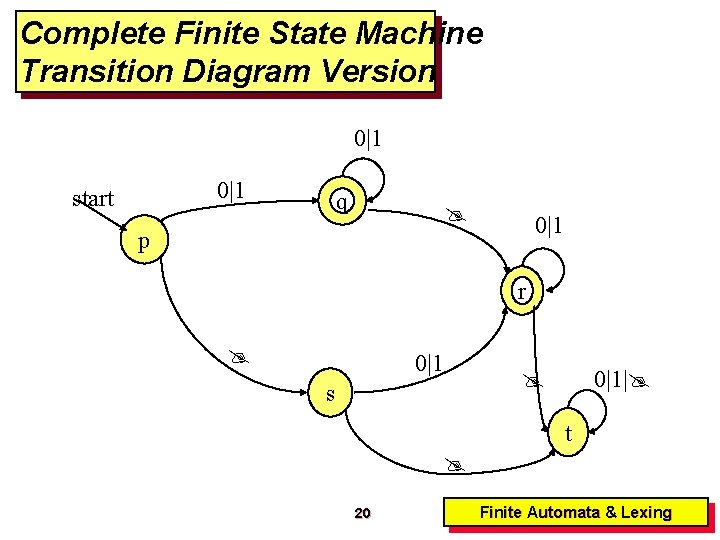
Complete Finite State Machine Transition Diagram Version 0|1 start q 0|1 p r 0|1 s 0|1| t 20 Finite Automata & Lexing

Non-deterministic FSMs • A FSM may have a choice of moves, i. e. is a mapping from Q to 2 Q. • Proposition. Let M 1 be a non-deterministic FSM. Then a DFSM M 2 for which L(M 2) = L(M 1). • Proposition. Given a NFSM, M, one can construct a right-linear cfg, G, for which L(G) = L(M), and conversely. 21 Finite Automata & Lexing

Extended Non-determinism • Besides allowing multiple moves on the same input symbol, we can allow moves on the empty string, ; i. e. for a given state q: (q, ) Q 22 Finite Automata & Lexing

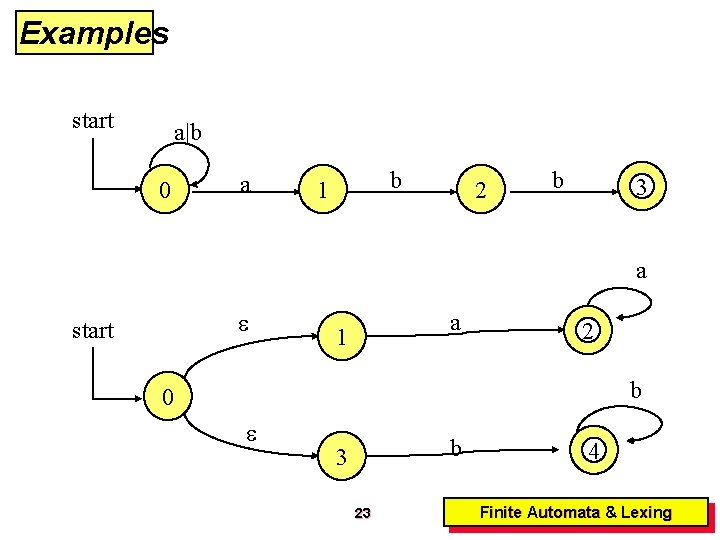
Examples start a|b 0 a b 1 2 b 3 a start a 1 2 b 0 b 3 23 4 Finite Automata & Lexing

Thompson’s Construction • Given a regular expression, r representing a regular set R, construct a non-deterministic finite state machine M that recognizes R, i. e. such that L(M)=R. 1) For construct start i 24 f Finite Automata & Lexing

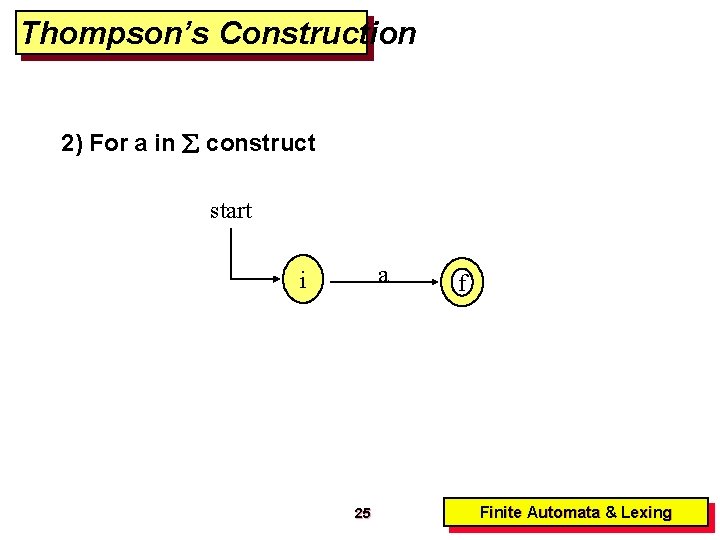
Thompson’s Construction 2) For a in construct start a i 25 f Finite Automata & Lexing

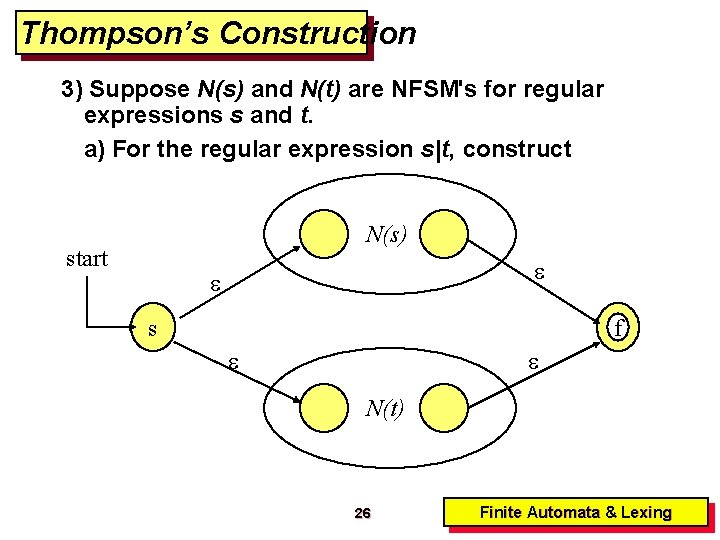
Thompson’s Construction 3) Suppose N(s) and N(t) are NFSM's for regular expressions s and t. a) For the regular expression s|t, construct N(s) start s f N(t) 26 Finite Automata & Lexing

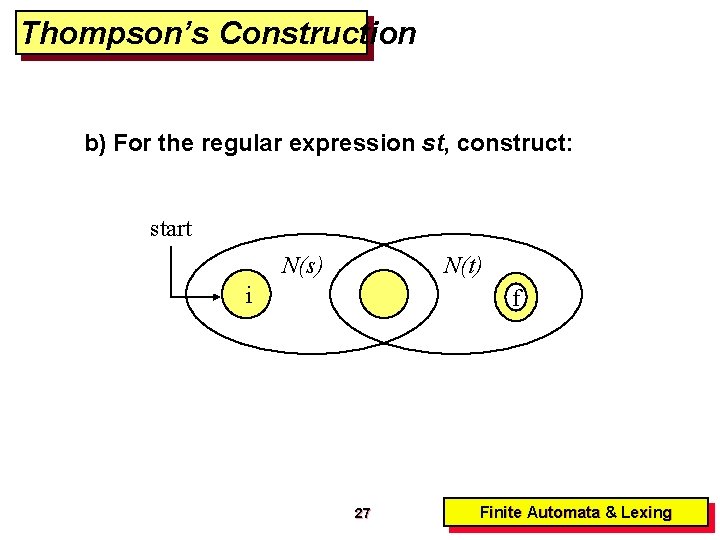
Thompson’s Construction b) For the regular expression st, construct: start N(s) N(t) i f 27 Finite Automata & Lexing

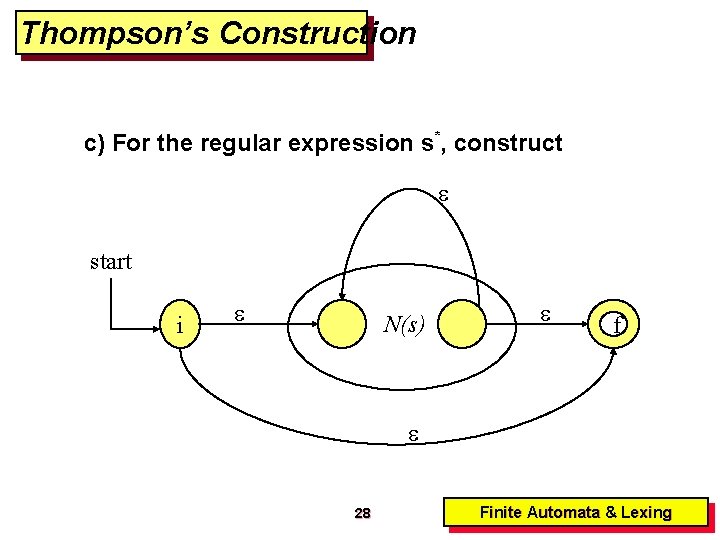
Thompson’s Construction c) For the regular expression s*, construct start i N(s) f 28 Finite Automata & Lexing

Transforming a NFSM to a DFSM (The Subset Construction) • Define: -closure(s Q) = {t Q | s can reach t via only -moves} -closure(T Q) = s T move(T Q, a ) = 29 -closure(s) s T (s, a) Finite Automata & Lexing

NFSM DFSM • Given M=(Q, , , q 0, F) define M’=(Q’, , ’, q’ 0, F’) by: 1) Compute q’ 0 = -closure(q 0). 2) Initialize Q’ with q’ 0 (unmarked). 3) while an unmarked element q’ of Q’: a) mark q’ b) a : -- compute p’ = -closure(move(q’, a)) -- if p’ Q’ then add p’ (unmarked) to Q’ -- set ’(q’, a)=p’ 4) F’ = { q’ Q’ | q q’ q F} 30 Finite Automata & Lexing

Example • Perform Thompson’s Construction on (a|b)*abb to obtain a non-deterministic finite state machine. • Perform the subset construction to make it deterministic. 31 Finite Automata & Lexing

Simulating a DFSM s: = q 0 a: =nextchar while a eof { s: = (s, a) a: =nextchar } if s F then return “yes” else return “no” 32 Finite Automata & Lexing

Simulating a NFSM S: = -closure({q 0}) a: =nextchar while a eof { S: = -closure(move(S, a)) a: =nextchar } if S F then return “yes” else return “no” 33 Finite Automata & Lexing

Transforming from NFSM to Right-Linear CFG • Given M=(Q, , , q 0, F), construct G=(Q, , P, q 0) where 1) q F include in P q 2) q 1, q 2 Q; a q 2 (q 1, a) include in P q 1 a q 2 3) q 1, q 2 Q q 2 (q 1, ) include in P q 1 q 2 34 Finite Automata & Lexing

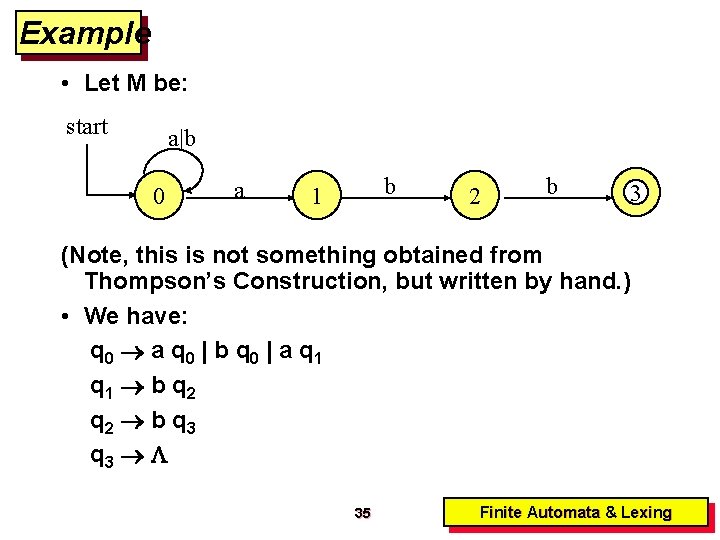
Example • Let M be: start a|b 0 a b 1 2 b 3 (Note, this is not something obtained from Thompson’s Construction, but written by hand. ) • We have: q 0 a q 0 | b q 0 | a q 1 b q 2 b q 3 35 Finite Automata & Lexing

RLG Regular Expression • The algorithm resembles Gaussian Elimination. • Notice that all of the “A-rules” can be “grouped” by the non-terminal on the right side of the rightpart and “factored”: A 0 A A 1 A 1 A 2 A 2 … A n-1 An-1 A n where the i are regular expressions over 36 Finite Automata & Lexing

RLG Regular Expression • Then A can be written as the following regular expression over V: A = 0*( 1 A 1 | 2 A 2 | … | n-1 An-1 | n ) and the above regular expression can be substituted for A everywhere A appears in the grammar. • Following that, all rules can again be written in the foregoing “factored” form. 37 Finite Automata & Lexing

RLG Regular Expression • Given a right-linear grammar G=(N, . P, S): A) repeat 1) write all rules in “factored” form. 2) choose some non-terminal, A S, to eliminate. 3) compute the regular expression, r, which is equivalent to A, and substitute r in place of A everywhere in G. 4) delete all A-rules from G until only S-rules remain B) compute the regular expression, r, to which S is equivalent. 38 Finite Automata & Lexing

Example • Recall q 0 a q 0 | b q 0 | a q 1 b q 2 b q 3 • Rewrite q 0 (a | b) q 0 | a q 1 b q 2 b q 3 39 Finite Automata & Lexing

Example • Eliminate q 3 • Eliminate q 2 • Eliminate q 1 • Compute q 0 (a | b) q 0 | a q 1 b q 2 b q 0 (a | b) q 0 | a q 1 b b q 0 (a | b) q 0 | a b b q 0 = (a | b)* a b b 40 Finite Automata & Lexing

Limitations of FSMs • FSMs have a fixed numbers of states • For this reason, there are objects that cannot be recognized by FSMs. • For example there is no FSM that can recognize palindromes of arbitrary length. • The DO keyword in Fortran cannot be expressed as a regular expression. 41 Finite Automata & Lexing

Minimization of DFSM’s • Well-known algorithm (due to Hopcroft), useful in many other circumstances. 1) Initially partition Q into two groups, F and Q-F. 2) repeat group, G, of the partition, split G into multiple sub-groups, if incompatible transitions are found among members of G. until no further changes occur 42 Finite Automata & Lexing

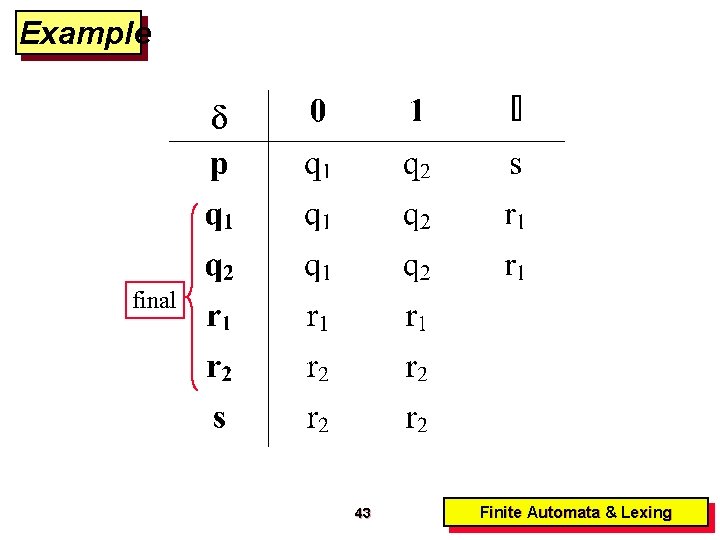
Example final 43 Finite Automata & Lexing

Algebraic Properties 44 Finite Automata & Lexing

Shorthand Notations • (a)+ denotes one or more instance r* = r+ | r+ = rr* • (r)? denotes zero or one instance r? = r | • [a-z] denotes a|b|c|. . |z 45 Finite Automata & Lexing

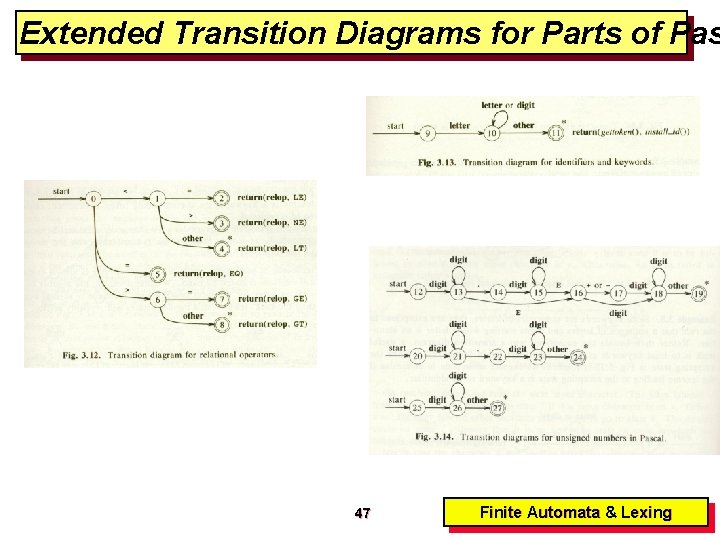
Examples • [a-z. A-Z]+ denotes string of one or more characters • [a-z. A-Z][a-z. A-Z 0 -9] + denotes valid identifiers in Fortran • [0 -9] +(. [0 -9] +)? (E(+|-)? [0 -9] +)? denotes valid unsigned Pascal numbers 46 Finite Automata & Lexing

Extended Transition Diagrams for Parts of Pas 47 Finite Automata & Lexing