CS 240 Lecture 8 Bitwise Operations Bit Manipulation

CS 240 – Lecture 8 Bitwise Operations, Bit Manipulation, Type Conversion, Conditional Expression

Operators – Bitwise Operations • Bitwise operations are operations that are performed at the binary bit level on a value. • The logic for these operations comes from the function of their corresponding logic gate in electronics and circuitry. • You'll be working with these more in CS 341. 1010 1100 • In programming, these elementary operations are often helpful for solving problems at the higher level, so they're included into the language.

Operators – Bitwise AND & • The Bitwise AND (&) operator takes two numeric operands and gives a single numeric in response. char flags = flags & 0 x 0 F; 1010 1100 • For each column of bits across both numbers, & 0000 1111 the resultant value will have a 1 bit only if both = 0000 1100 bits from the operands are 1. • Otherwise, the bit for that column in the result is 0. • It doesn't matter which order the operands are in (commutativity). • However, generally, it's said that the second operand is "turning off flags" in the first operand.

Operators – Bitwise OR | • The Bitwise OR (|) operator takes two numeric operands and gives a single numeric in response. 1010 1100 char flags = flags | 0 x 0 F; | 0000 1111 • For each column of bits across both numbers, the resultant value will have a 1 bit only if at least = 1010 1111 one bit from the operands are 1. • Otherwise, the bit for that column in the result is 0. • The Bitwise OR is also commutative. • It's said that the second operand is "turning on flags" in the first operand.

Operators – Bitwise XOR ^ • The Bitwise XOR or Exclusive OR (^) operator takes two numeric operands and gives a single numeric in response. • This is NOT the Exponent Operator and NOT how you take bases to powers! char flags = flags ^ 0 x 0 F; 1010 1100 • For each column of bits across both numbers, ^ 0000 1111 the resultant value will have a 1 bit only if exactly = 1010 0011 one bit from the operands are 1. • You can also think of it as the 1 bits from the second operand "flipping" the bits of the first operand. (Note: 0 does not flip anything) • This operation is also commutative.

Operators – Bitwise NOT ~ / One's Comp. • We've actually already covered Bitwise NOT (~) before as a concept, rather than an operator. ~ 0101 1100 • It's the One's Complement! char flags = ~flags; = 1010 0011 • It's a unary operator which operates on numeric values. • For each bit in the operand, the resultant value has that bit flipped. • This is mathematically equivalent to (–x – 1)

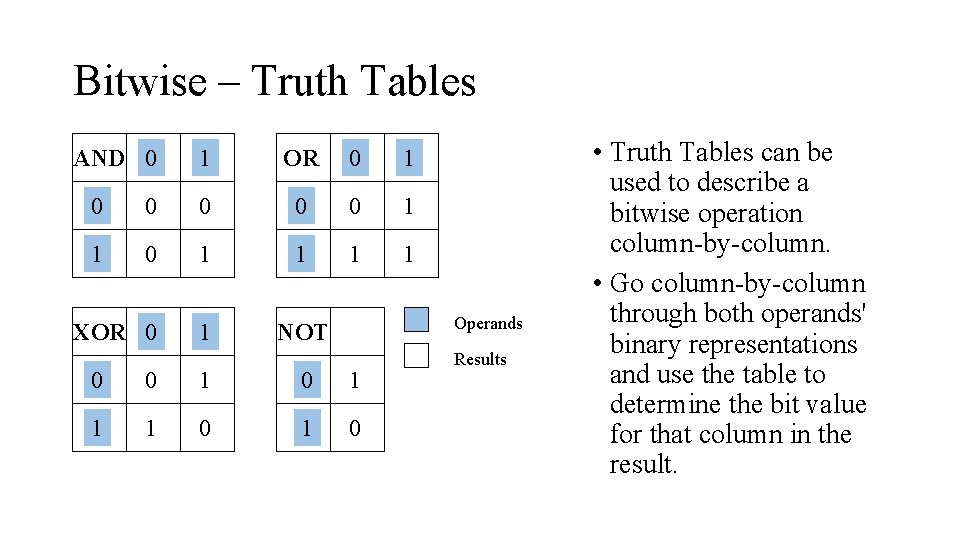
Bitwise – Truth Tables AND 0 1 OR 0 1 0 0 0 1 1 1 1 XOR 0 1 NOT Operands 0 0 1 1 1 0 Results • Truth Tables can be used to describe a bitwise operation column-by-column. • Go column-by-column through both operands' binary representations and use the table to determine the bit value for that column in the result.

Bitwise – Hexwise • Any bitwise operation can be done equivalently on other power-of-two representations of the numbers. 0 0000 8 1000 • We can do this for hexadecimal by grouping 1 0001 9 1001 2 0010 A 1010 the binary digits into fours and replacing 3 0011 B 1011 them with their hexadecimal digits. • Note, since the bitwise operations are always the same for the groups of four bits, they'll be the same for the hex digits. 7 F 0111 1111 & A 0 & 1010 0000 = 20 = 0010 0000 4 0100 C 1100 5 0101 D 1101 6 0110 E 1110 7 0111 F 1111

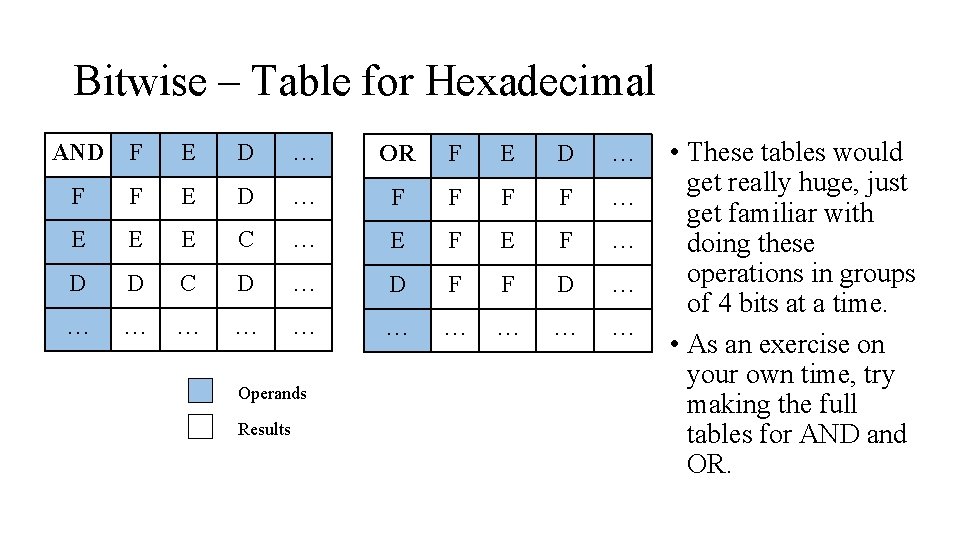
Bitwise – Table for Hexadecimal AND F E D … OR F E D … F F F F … E E E C … E F … D D C D … D F F D … … … Operands Results • These tables would get really huge, just get familiar with doing these operations in groups of 4 bits at a time. • As an exercise on your own time, try making the full tables for AND and OR.

Examples - Bitwise Operations & and | 1010 1100 1101 0 x 1111 & 0000 & 1111 & 0000 1111 & 0 x 9999 = 0000 = 1010 1100 = 0000 1101 = 0 x 1111 1010 1100 1101 0010 0 x 1111 | 0000 | 1111 | 0000 1111 | 0 x 8888 = 1010 1100 = 1111 = 1101 1111 = 0 x 9999

Examples - Bitwise Operations • The XOR operator requires a little more care in discussion. • Note that the last example of it can turn one message into another. 1010 1100 1101 0010 0 x. CAFEBABE ^ 0000 ^ 1111 ^ 0000 1111 ^ 0 x 74117070 = 1010 1100 = 0101 0011 = 1101 = 0 x. BEEFCACE

Encryption with XOR • One very powerful property of XOR that the other bitwise operations don't have is the recoverability of past operands. newx = x ^ key; oldx = newx ^ key; • This is possible because taking the XOR with respect to key gives us x with all of the key bits flipped. • If we do this twice, every bit in x is either never flipped or flipped twice (which brings it back to it's starting point). x ^ n = x ^ 0 = x for all x and n

Type Conversion – String to Numeric atoi • We learned last week how to work with fscanf to read numeric values from input. • However, once values are already in memory as strings, fscanf won't help us work with them as numeric values. int num = atoi(str); • In stdlib. h, there is a function called atoi which converts a number in a string to a numeric int value. • The function ignores any whitespace characters before the representation in the buffer given and it can be followed by any non-numeric characters. • Will return 0 on failure to find a numeric string at the beginning of the buffer.

Type Conversion – How to implement atoi • Remember from previous lectures that every digit in decimal representation is the coefficient of a power of 10. • To implement atoi, we simply need to take each ASCII digit to it's numeric counterpart ('0' 0) • Then multiply it by the power of 10 corresponding to that column. • Finally, total everything up and that's the numeric value of that string. int atoi(char s[ ]) { int i, n = 0; for (i=0; s[i] >= '0' && s[i] <= '9'; ++i) n = 10 * n + (s[i] - '0'); return n; }

Fundamentals – Conditional Expression ? : • This is one of the only ternary operations you’re likely to find in most programming languages. • An operation that takes 3 operands. int max = (a > b) ? a : b; • The conditional (? : ) operator is an in-place if-expression which has three parts: the condition, then-value, and the else-value. • If the condition is non-zero (true), the entire expression evaluates to then-value. • Otherwise, the entire expression evaluates to the else-value.