CS 240 A Linear Algebra in Shared Memory

CS 240 A : Linear Algebra in Shared Memory with Cilk++ • Matrix-matrix multiplication • Matrix-vector multiplication • Hyperobjects Thanks to Charles E. Leiserson for some of these slides 1

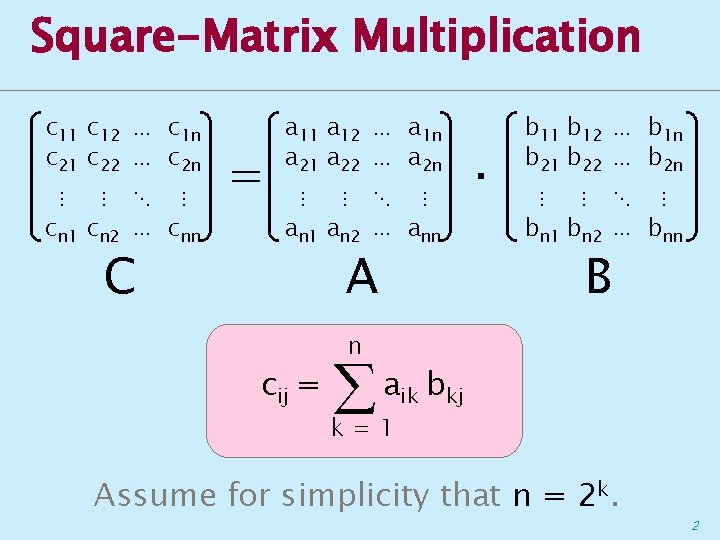
Square-Matrix Multiplication c 11 c 12 ⋯ c 1 n c 21 c 22 ⋯ c 2 n ⋮ ⋮ ⋱ ⋮ cn 1 cn 2 ⋯ cnn C = a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ an 1 an 2 ⋯ ann A cij = n · b 11 b 12 ⋯ b 1 n b 21 b 22 ⋯ b 2 n ⋮ ⋮ ⋱ ⋮ bn 1 bn 2 ⋯ bnn B aik bkj k=1 Assume for simplicity that n = 2 k. 2

Parallelizing Matrix Multiply cilk_for (int i=1; i<n; ++i) { cilk_for (int j=0; j<n; ++j) { for (int k=0; k<n; ++k { C[i][j] += A[i][k] * B[k][j]; } } Work: T 1 = Θ(n 3) Span: T∞ = Θ(n) Parallelism: T 1/T∞ = Θ(n 2) For 1000 × 1000 matrices, parallelism ≈ (103)2 = 106. 3

Recursive Matrix Multiplication Divide and conquer — C 11 C 12 C 21 C 22 = = A 11 A 12 A 21 A 22 A 11 B 11 A 11 B 12 A 21 B 11 A 21 B 12 · + B 11 B 12 B 21 B 22 A 12 B 21 A 12 B 22 A 22 B 21 A 22 B 22 8 multiplications of n/2 × n/2 matrices. 1 addition of n × n matrices. 4

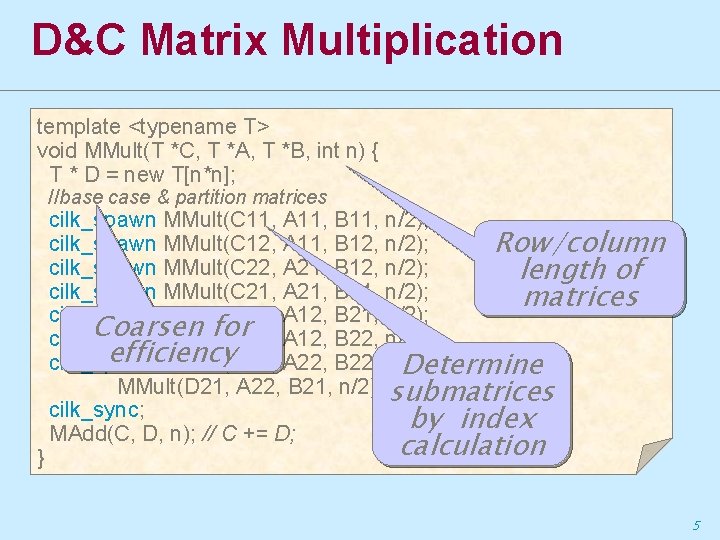
D&C Matrix Multiplication template <typename T> void MMult(T *C, T *A, T *B, int n) { T * D = new T[n*n]; //base case & partition matrices } cilk_spawn MMult(C 11, A 11, B 11, n/2); cilk_spawn MMult(C 12, A 11, B 12, n/2); Row/column cilk_spawn MMult(C 22, A 21, B 12, n/2); length of cilk_spawn MMult(C 21, A 21, B 11, n/2); matrices cilk_spawn MMult(D 11, A 12, B 21, n/2); Coarsen for A 12, B 22, n/2); cilk_spawn MMult(D 12, efficiency cilk_spawn MMult(D 22, A 22, B 22, n/2); Determine MMult(D 21, A 22, B 21, n/2); submatrices cilk_sync; by index MAdd(C, D, n); // C += D; calculation 5

Matrix Addition template <typename T> void MMult(T *C, T *A, T *B, int n) { T * D = new T[n*n]; //base case & partition matrices cilk_spawn MMult(C 11, A 11, B 11, n/2); cilk_spawn MMult(C 12, A 11, B 12, n/2); cilk_spawn MMult(C 22, A 21, B 12, n/2); cilk_spawn MMult(C 21, A 21, B 11, n/2); cilk_spawn MMult(D 11, A 12, B 21, n/2); <typename T>n/2); cilk_spawntemplate MMult(D 12, A 12, B 22, MAdd(T A 22, *C, TB 22, *D, int n) { cilk_spawnvoid MMult(D 22, n/2); cilk_for. A 22, (int i=0; ++i) { MMult(D 21, B 21, i<n; n/2); cilk_for (int j=0; j<n; ++j) { cilk_sync; += D[n*i+j]; MAdd(C, D, n); C[n*i+j] // C += D; } } 6

Analysis of Matrix Addition template <typename T> void MAdd(T *C, T *D, int n) { cilk_for (int i=0; i<n; ++i) { cilk_for (int j=0; j<n; ++j) { C[n*i+j] += D[n*i+j]; } } } Work: A 1(n) = Θ(n 2) Span: A∞(n) = Θ(lg n) Nested cilk_for statements have the same Θ(lg n) span 7

Work of Matrix Multiplication template <typename T> void MMult(T *C, T *A, T *B, int n) { T * D = new T [n*n]; //base case & partition matrices } cilk_spawn MMult(C 11, A 11, B 11, n/2); CASE 1: cilk_spawn MMult(C 12, A 11, B 12, n/2); nlogba = nlog 28 = ⋮ cilk_spawn MMult(D 22, A 22, B 22, f(n) n/2); = Θ(n 2) MMult(D 21, A 22, B 21, n/2); cilk_sync; MAdd(C, D, n); // C += D; n 3 Work: M 1(n) = 8 M 1(n/2) + A 1(n) + Θ(1) = 8 M 1(n/2) + Θ(n 2) = Θ(n 3) 8

Span of Matrix Multiplication template <typename T> void MMult(T *C, T *A, T *B, int n) { T * D = new T [n*n]; maximum //base case & partition matrices } cilk_spawn MMult(C 11, A 11, B 11, n/2); 2: cilk_spawn MMult(C 12, A 11, CASE B 12, n/2); ⋮ nlogba = nlog 21 = 1 cilk_spawn MMult(D 22, A 22, B 22, n/2); log a 1 MMult(D 21, A 22, B 21, f(n) n/2); = Θ(n b lg n) cilk_sync; MAdd(C, D, n, size); // C += D; Span: M∞(n) = M∞(n/2) + A∞(n) + Θ(1) = M∞(n/2) + Θ(lg n) = Θ(lg 2 n) 9

Parallelism of Matrix Multiply Work: M 1(n) = Θ(n 3) Span: M∞(n) = Θ(lg 2 n) Parallelism: M 1(n) M∞(n) = Θ(n 3/lg 2 n) For 1000 × 1000 matrices, parallelism ≈ (103)3/102 = 107. 10

Stack Temporaries template <typename T> void MMult(T *C, T *A, T *B, int n) { T * D = new T [n*n]; //base case & partition matrices } cilk_spawn MMult(C 11, A 11, B 11, n/2); cilk_spawn MMult(C 12, A 11, B 12, n/2); cilk_spawn MMult(C 22, A 21, B 12, n/2); cilk_spawn MMult(C 21, A 21, B 11, n/2); cilk_spawn MMult(D 11, A 12, B 21, n/2); cilk_spawn MMult(D 12, A 12, B 22, n/2); cilk_spawn MMult(D 22, A 22, B 22, n/2); MMult(D 21, A 22, B 21, n/2); cilk_sync; MAdd(C, D, n); // C += D; IDEA: Since minimizing storage tends to yield higher performance, trade off parallelism for less storage. 11

No-Temp Matrix Multiplication // C += A*B; template <typename T> void MMult 2(T *C, T *A, T *B, int n) { //base case & partition matrices } cilk_spawn MMult 2(C 11, A 11, B 11, n/2); cilk_spawn MMult 2(C 12, A 11, B 12, n/2); cilk_spawn MMult 2(C 22, A 21, B 12, n/2); MMult 2(C 21, A 21, B 11, n/2); cilk_sync; cilk_spawn MMult 2(C 11, A 12, B 21, n/2); cilk_spawn MMult 2(C 12, A 12, B 22, n/2); cilk_spawn MMult 2(C 22, A 22, B 22, n/2); MMult 2(C 21, A 22, B 21, n/2); cilk_sync; Saves space, but at what expense? 12

Work of No-Temp Multiply // C += A*B; template <typename T> void MMult 2(T *C, T *A, T *B, int n) { //base case & partition matrices } cilk_spawn MMult 2(C 11, A 11, B 11, n/2); cilk_spawn MMult 2(C 12, A 11, B 12, n/2); cilk_spawn MMult 2(C 22, A 21, B 12, n/2); MMult 2(C 21, A 21, B 11, CASE n/2); 1: cilk_sync; log a = nlog 28 cilk_spawn MMult 2(C 11, A 12, n B 21, bn/2); cilk_spawn MMult 2(C 12, A 12, B 22, n/2); = Θ(1) cilk_spawn MMult 2(C 22, A 22, f(n) B 22, n/2); MMult 2(C 21, A 22, B 21, n/2); cilk_sync; = n 3 Work: M 1(n) = 8 M 1(n/2) + Θ(1) = Θ(n 3) 13

Span of No-Temp Multiply // C += A*B; template <typename T> void MMult 2(T *C, T *A, T *B, int n) { //base case & partition matrices max } cilk_spawn MMult 2(C 11, A 11, B 11, n/2); cilk_spawn MMult 2(C 12, A 11, B 12, n/2); cilk_spawn MMult 2(C 22, A 21, B 12, n/2); MMult 2(C 21, A 21, B 11, CASE n/2); 1: cilk_sync; log a = nlog 22 cilk_spawn MMult 2(C 11, A 12, n B 21, bn/2); cilk_spawn MMult 2(C 12, A 12, B 22, n/2); = Θ(1) cilk_spawn MMult 2(C 22, A 22, f(n) B 22, n/2); MMult 2(C 21, A 22, B 21, n/2); cilk_sync; =n Span: M∞(n) = 2 M∞(n/2) + Θ(1) = Θ(n) 14

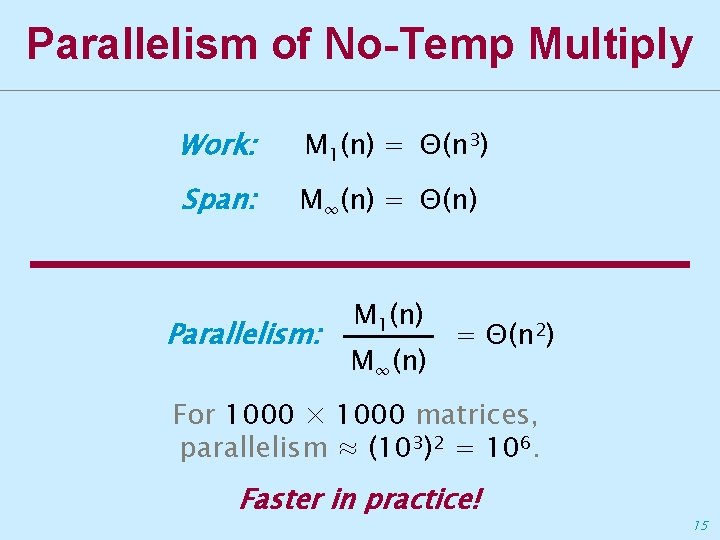
Parallelism of No-Temp Multiply Work: M 1(n) = Θ(n 3) Span: M∞(n) = Θ(n) Parallelism: M 1(n) M∞(n) = Θ(n 2) For 1000 × 1000 matrices, parallelism ≈ (103)2 = 106. Faster in practice! 15

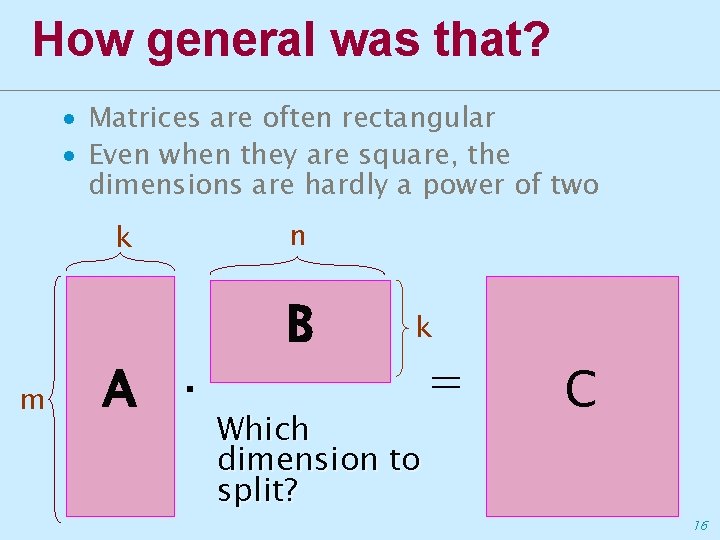
How general was that? ∙ Matrices are often rectangular ∙ Even when they are square, the dimensions are hardly a power of two k m A · n B k Which dimension to split? = C 16

General Matrix Multiplication template <typename T> void MMult 3(T *A, T* B, T* C, int i 0, int i 1, int j 0, int j 1, int k 0, int k 1) { Split m if it is int di = i 1 - i 0; int dj = j 1 - j 0; int dk = k 1 - k 0; if (di >= dj && di >= dk && di >= THRESHOLD)the { largest int mi = i 0 + di / 2; MMult 3 (A, B, C, i 0, mi, j 0, j 1, k 0, k 1); MMult 3 (A, B, C, mi, i 1, j 0, j 1, k 0, k 1); Split n if it is the } else if (dj >= dk && dj >= THRESHOLD) { int mj = j 0 + dj / 2; largest MMult 3 (A, B, C, i 0, i 1, j 0, mj, k 0, k 1); MMult 3 (A, B, C, i 0, i 1, mj, j 1, k 0, k 1); } else if (dk >= THRESHOLD) { Split k if it is the int mk = k 0 + dk / 2; largest MMult 3 (A, B, C, i 0, i 1, j 0, j 1, k 0, mk); MMult 3 (A, B, C, i 0, i 1, j 0, j 1, mk, k 1); } else { // Iterative (triple-nested loop) multiply } } for (int i = i 0; i < i 1; ++i) { for (int j = j 0; j < j 1; ++j) { for (int k = k 0; k < k 1; ++k) C[i][j] += A[i][k] * B[k][j]; 17

Parallelizing General MMult template <typename T> void MMult 3(T *A, T* B, T* C, int i 0, int i 1, int j 0, int j 1, int k 0, int k 1) { int di = i 1 - i 0; int dj = j 1 - j 0; int dk = k 1 - k 0; if (di >= dj && di >= dk && di >= THRESHOLD) { int mi = i 0 + di / 2; cilk_spawn MMult 3 (A, B, C, i 0, mi, j 0, j 1, k 0, k 1); MMult 3 (A, B, C, mi, i 1, j 0, j 1, k 0, k 1); } else if (dj >= dk && dj >= THRESHOLD) { int mj = j 0 + dj / 2; cilk_spawn MMult 3 (A, B, C, i 0, i 1, j 0, mj, k 0, k 1); to spawn Unsafe MMult 3 (A, B, C, i 0, i 1, mj, j 1, k 0, k 1); here unless we use } else if (dk >= THRESHOLD) { a temporary ! int mk = k 0 + dk / 2; MMult 3 (A, B, C, i 0, i 1, j 0, j 1, k 0, mk); MMult 3 (A, B, C, i 0, i 1, j 0, j 1, mk, k 1); } else { // Iterative (triple-nested loop) multiply } } for (int i = i 0; i < i 1; ++i) { for (int j = j 0; j < j 1; ++j) { for (int k = k 0; k < k 1; ++k) C[i][j] += A[i][k] * B[k][j]; 18

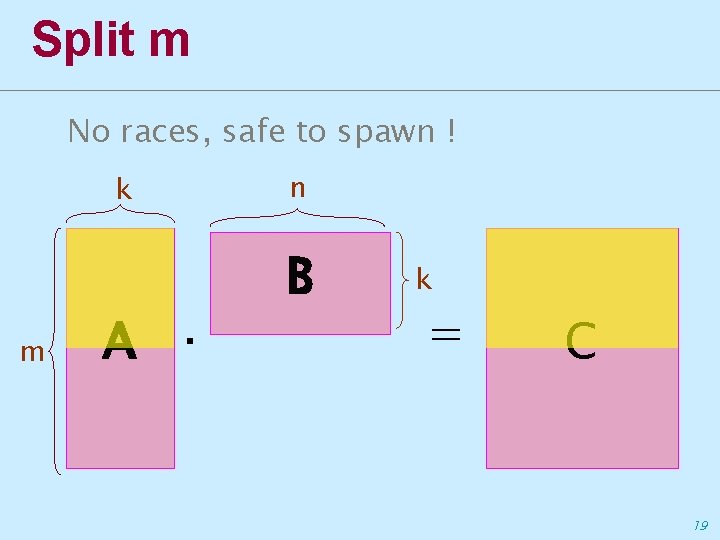
Split m No races, safe to spawn ! k m A · n B k = C 19

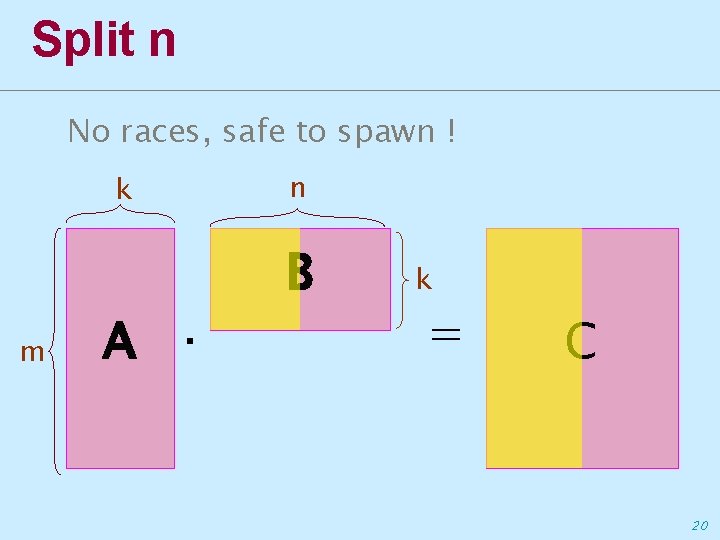
Split n No races, safe to spawn ! k m A · n B k = C 20

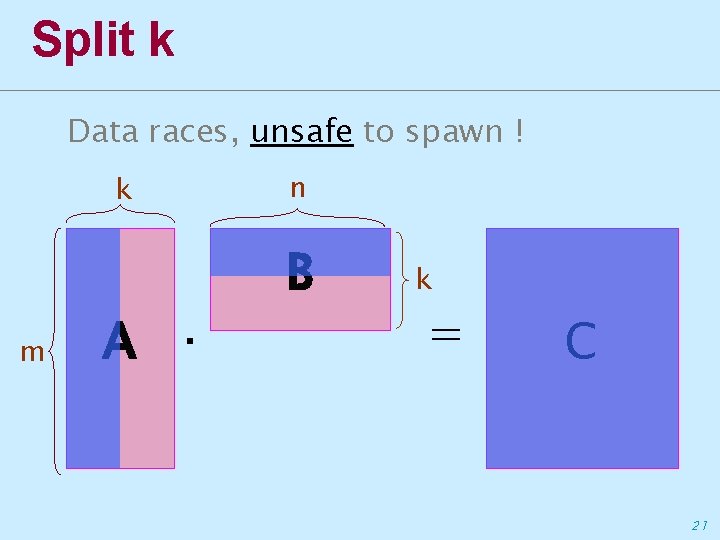
Split k Data races, unsafe to spawn ! k m A · n B k = C 21

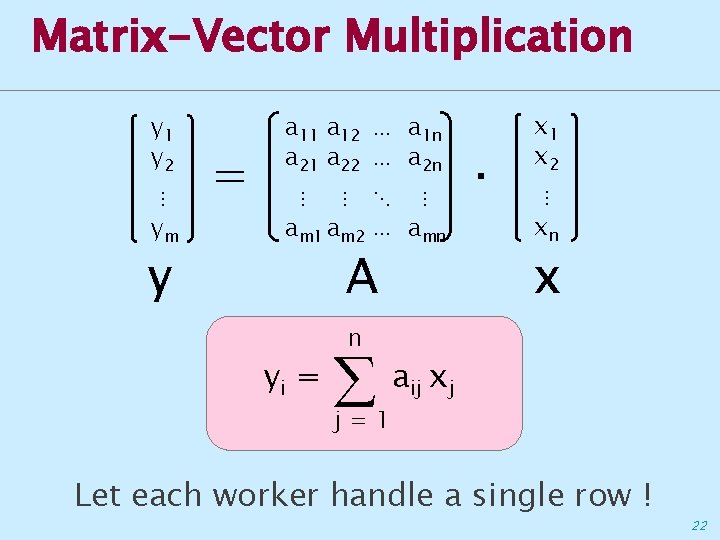
Matrix-Vector Multiplication y 1 y 2 ⋮ ym y = a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ am 1 am 2 ⋯ amn A yi = n j=1 · x 1 x 2 ⋮ xn x aij xj Let each worker handle a single row ! 22

Matrix-Vector Multiplication template <typename T> void Mat. Vec (T **A, T* x, T* y, int m, int n) { for(int i=0; i<m; i++) { for(int j=0; j<n; j++) y[i] += A[i][j] * x[j]; } } Parallelize template <typename T> void Mat. Vec (T **A, T* x, T* y, int m, int n) { cilk_for (int i=0; i<m; i++){ for(int j=0; j<n; j++) y[i] += A[i][j] * x[j]; } } 23

Matrix-Transpose x Vector y 1 y 2 ⋮ yn y = a 11 a 21 ⋯ am 1 a 12 a 22 ⋯ am 2 ⋮ ⋮ ⋱ ⋮ a 1 n a 2 n ⋯ amn T A yi = m a j=1 ji · x 1 x 2 ⋮ xm x xj The data is still A, no explicit transposition 24

Matrix-Transpose x Vector template <typename T> void Mat. Trans. Vec (T **A, T* x, T* y, int m, int n) { cilk_for(int i=0; i<n; i++) { for(int j=0; j<m; j++) y[i] += A[j][i] * x[j]; Terrible performance } (1 cache-miss/iteration) } Reorder loops template <typename T> void Mat. Trans. Vec (T **A, T* x, T* y, int m, int n) { cilk_for (int j=0; j<m; j++){ for(int i=0; i<n; i++) y[i] += A[j][i] * x[j]; } Data Race ! } 25

Hyperobjects ∙ Avoiding the data race on the variable y can be done by splitting y into multiple copies that are never accessed concurrently. ∙ A hyperobject is a Cilk++ object that shows distinct views to different observers. ∙ Before completing a cilk_sync, the parent’s view is reduced into the child’s view. ∙ For correctness, the reduce() function should be associative (not necessarily commutative). template <typename T> struct add_monoid: cilk: : monoid_base<T> { void reduce (T * left, T * right) const { *left += *right; } … } 26

Hyperobject solution ∙ Use a built-in hyperobject (there are many, read the REDUCERS chapter from the programmer’s guide) template <typename T> void Mat. Trans. Vec (T **A, T* x, T* y, int m, int n) { array_reducer_t art(n, y); cilk: : hyperobject<array_reducer_t> rvec(art); cilk_for (int j=0; j<m; j++){ T * array = rvec(). array; for(int i=0; i<n; i++) array[i] += A[j][i] * x[j]; } } ∙ Use hyperobjects sparingly, on infrequently accessed global variable. ∙ This example is for educational purposes. There are better ways of parallelizing y=ATx. 27