CS 235102 Data Structures Chapter 9 Heap Structures

CS 235102 Data Structures Chapter 9 Heap Structures

§ Min-Max Heap § Deaps § Leftist Trees § Binomial Heaps § Fibonacci Heaps

MIN-MAX Heaps (1/10) § Definition § A double-ended priority queue is a data structure that supports the following operations: § Insert an element with arbitrary key § Delete an element with the largest key § Delete an element with the smallest key § Min heap or Max heap: § Only insertion and one of the two deletion operations are supported § Min-Max heap: § Supports all of the operations just described.

§ Definition: MIN-MAX Heaps (2/10) § A mix-max heap is a complete binary tree such that if it is not empty, each element has a field called key. § Alternating levels of this tree are min levels and max levels, respectively. § Let x be any node in a min-max heap. If x is on a min (max) level then the element in x has the minimum (maximum) key from among all elements in the subtree with root x. We call this node a min (max) node.

MIN-MAX Heaps (3/10) § Insertion into a min-max heap (at a “max” level) § If it is smaller/greater than its father (a “min”), then it must be smaller/greater than all “max”/“min” above. So simply check the “min”/“max” ancestors § There exists a similar approach at a “min” level

§ verify_max MIN-MAX Heaps (4/10) § Following the nodes the max node i to the root and insert into its proper place item = 80 i=3 13 grandparent = 0 3 #define MAX_SIZE 100 #define FALSE 0 #define TRUE 1 #define SWAP(x, y, t) ((t)=(x), (x)=(y), (y)=(t)) typedef struct { int key; /* other fields */ }element; element [1 ] [2 ] [4 [8] ] [9 ] [3 ] [5 [10] [11 ] ] [6 [12] [13 ] ] 40 80 [7 ]

MIN-MAX Heaps (5/10) § min_max_insert: Insert item into the min-max heap item. key = 80 5 *n = 14 12 13 parent = 7 6 [1 ] [2 70 ] [4 [5 30 ] 9 ] 45 50 30 complexity: O(log n) 57 min [3 40 80 ] [6 [7 710 ] 15 ] max 20 12 10 40 [8 [9 [10 [11 [12 [13 [14 min max

MIN-MAX Heaps (6/10) § Deletion of min element § If we wish to delete the element with the smallest key, then this element is in the root. § In general situation, we are to reinsert an element item into a min-max-heap, whose root is empty. § We consider the two cases: 1. The root has no children § Item is to be inserted into the root. 2. The root has at least one child. § The smallest key in the min-max-heap is in one of the children or grandchildren of the root. We determine the node k has the smallest key. § The following possibilities need to be considered:

MIN-MAX Heaps (7/10) a) item. key heap[k]. key § § No element in heap with key smaller than item. key Item may be inserted into the root. b) item. key heap[k]. key, k is a child of the root § § Since k is a max node, it has no descendants with key larger than heap[k]. key. Hence, node k has no descendants with key larger than item. key. heap[k] may be moved to the root and item inserted into node k.

MIN-MAX Heaps (8/10) c) item. key heap[k]. key, k is a grandchild of the root § § In this case, heap[k] may be moved to the root, now heap[k] is seen as presently empty. Let parent be the parent of k. If item. key heap[parent]. key, then interchange them. This ensures that the max node parent contains the largest key in the sub-heap with root parent. At this point, we are faced with the problem of inserting item into the sub-heap with root k. Therefore, we repeat the above process.

§ delete_min: complexity: O(log n) § Delete the minimum element from the min-max heap *n = 12 11 i=5 1 last = 5 k = 11 5 parent = 2 temp. key = x. key = 12 [1 ] [2 70 ] [4 [5 30 ] 912 ] 45 50 30 79 [0 ] 7 [3 40 ] [6 [7 10 ] 15 ] 20 12 [8 [9 [10 [11 [12

MIN-MAX Heaps (10/10) § Deletion of max element 1. Determine the children of the root which are located on max-level, and find the larger one (node) which is the largest one on the min-max heap 2. We would consider the node as the root of a max-min heap 3. There exist a similar approach (deletion of max element) as we mentioned above

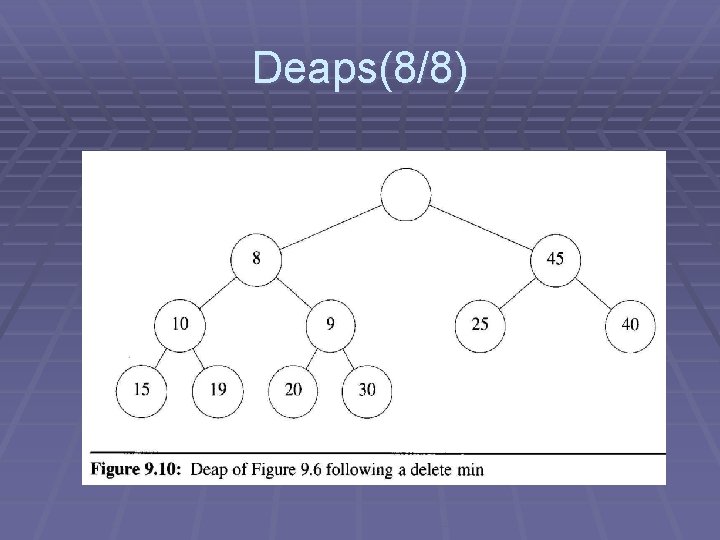
Deaps(1/8) § Definition § The root contains no element § The left subtree is a min-heap § The right subtree is a max-heap § Constraint between the two trees: § let i be any node in left subtree, j be the corresponding node in the right subtree. § if j not exists, let j corresponds to parent of i § i. key <= j. key

Deaps(2/8) § i = min_partner(n) = § j = max_partner(n) = § if j > heapsize j /= 2

Deaps Insert(3/8) public void insert(int x) { int i; if (++n == 2) { deap[2] = x; return; } if (in. Max. Heap(n)) { i = min. Partner(n); if (x < deap[i]) { deap[n] = deap[i]; min. Insert(i, x); } else max. Insert(n, x); } else { i = max. Partner(n); if (x > deap[i]) { deap[n] = deap[i]; max. Insert(i, x); } else min. Insert(n, x); } }

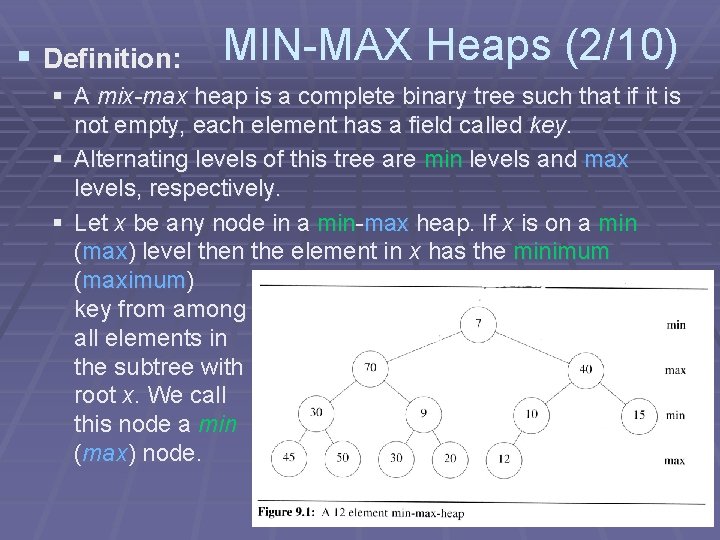
Deaps(4/8) § Insertion Into A Deap

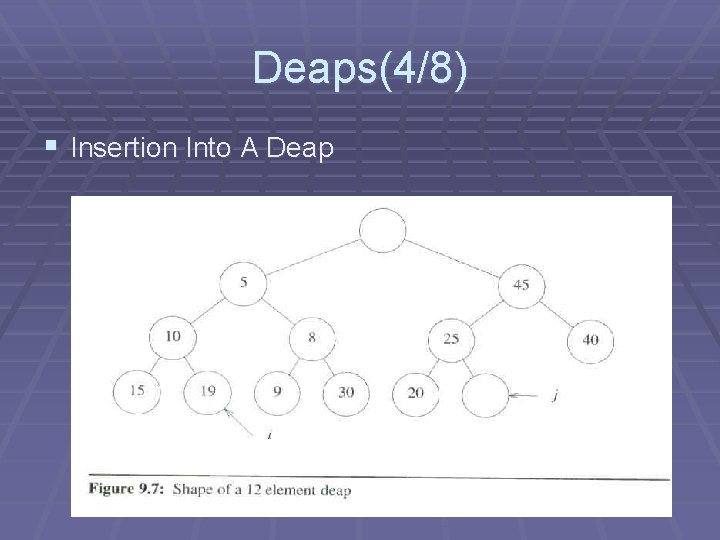
Deaps(5/8)

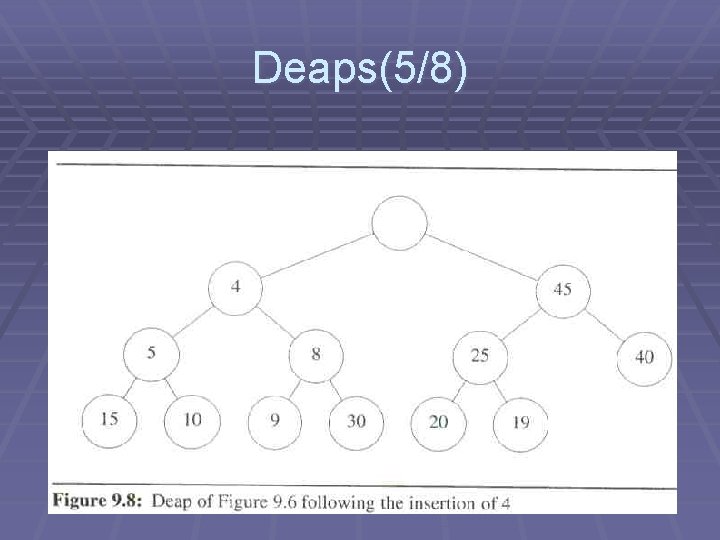
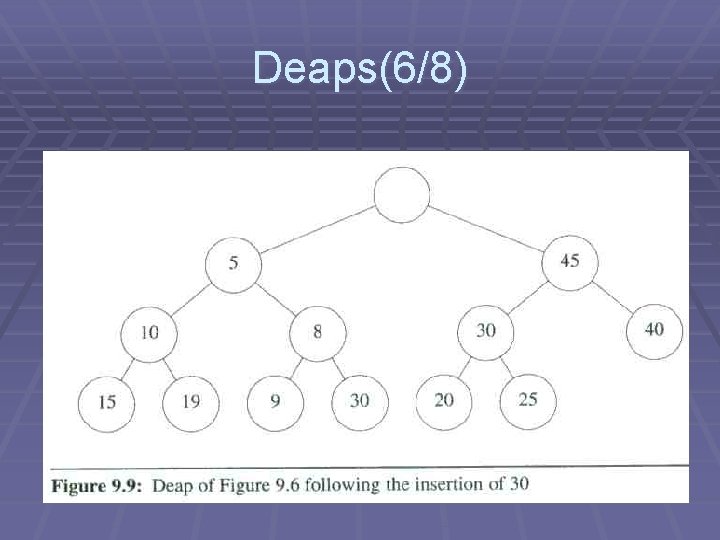
Deaps(6/8)

Deaps delete min(7/8) public int delete. Min() { int i, j, key = deap[2], x = deap[n--]; // move smaller child to i for (i = 2; 2*i <= n; deap[i] = deap[j], i = j) { j = i * 2; if (j+1 <= n && (deap[j] > deap[j+1]) j++; } // try to put x at leaf i j = max. Partner(i); if (x > deap[j]) { deap[i] = deap[j]; max. Insert(j, x); } else { min. Insert(i, x); } return key; }

Deaps(8/8)

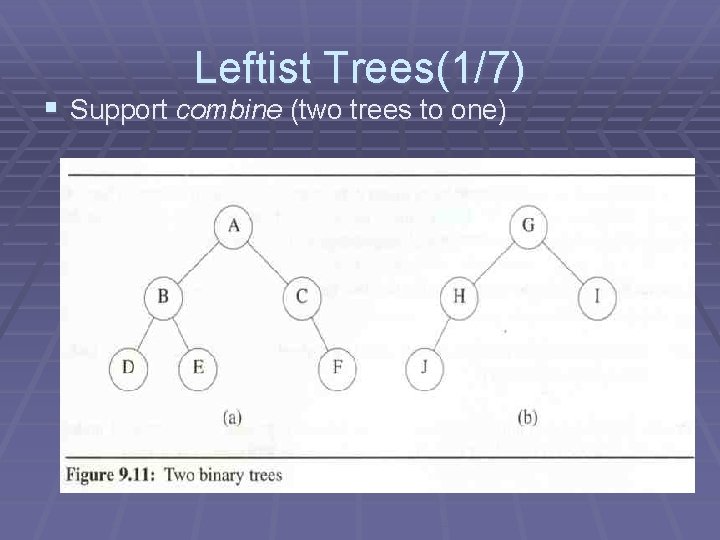
Leftist Trees(1/7) § Support combine (two trees to one)

§ § Leftist Trees(2/7) shortest(x) = 0 if x is an external node, otherwise 1+min(shortest(left(x)), shortest(right(x))}

Leftist Trees(3/7) § Definition: shortest(left(x)) >= shortest(right(x))

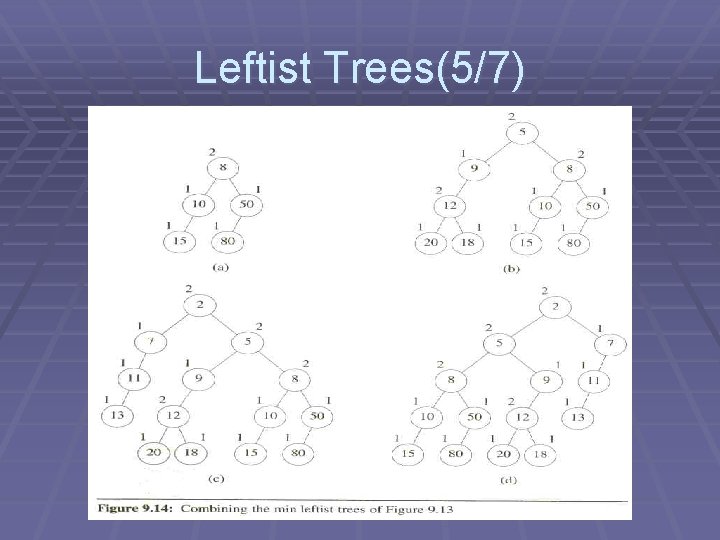
Leftist Trees(4/7) § Algorithm for combine(a, b) § assume a. data <= b. data § if (a. right is null) then make b be right child of a § else combine (a. right, b) § if shortest (a. right) > shortest (a. left) then exchange

Leftist Trees(5/7)

Leftist Trees(6/7)

Leftist Trees(7/7)

Binomial Heaps(1/10) § Cost Amortization(分期還款) § every operation in leftist trees costs O(logn) § actual cost of delete in Binomial Heap could be O(n), but insert and combine are O(1) § cost amortization charge some cost of a heavy operation to lightweight operations § amortized Binomial Heap delete is O(log 2 n) § A tighter bound could be achieved for a sequence of operations § actual cost of any sequence of i inserts, c combines, and dm delete in Binomial Heaps is O(i+c+dmlogi)

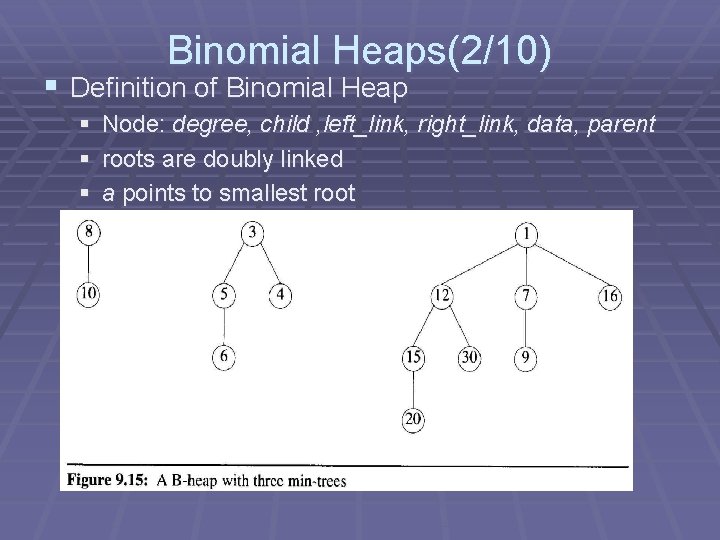
Binomial Heaps(2/10) § Definition of Binomial Heap § Node: degree, child , left_link, right_link, data, parent § roots are doubly linked § a points to smallest root

Binomial Heaps(3/10)

Binomial Heaps(4/10) § Insertion Into A Binomial Heaps § make a new node into doubly linked circular list pointed at by a § set a to the root with smallest key § Combine two B-heaps a and b § combine two doubly linked circular lists to one § set a to the root with smallest key

Binomial Heaps(5/10) § Deletion Of Min Element

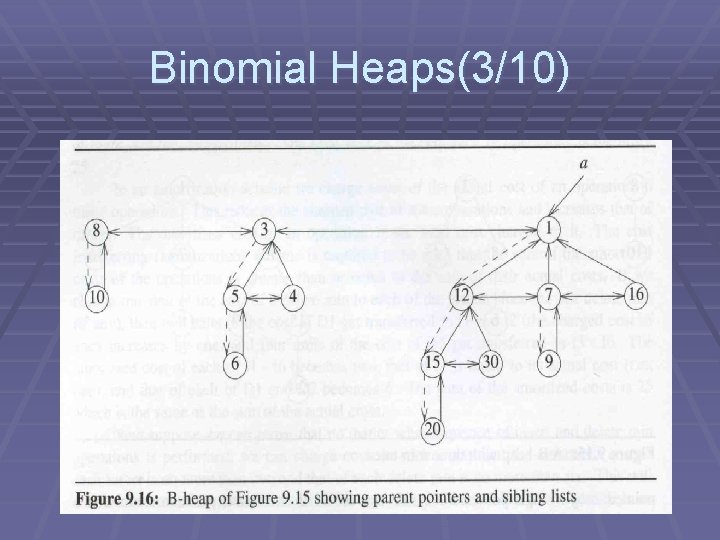
Binomial Heaps(6/10)

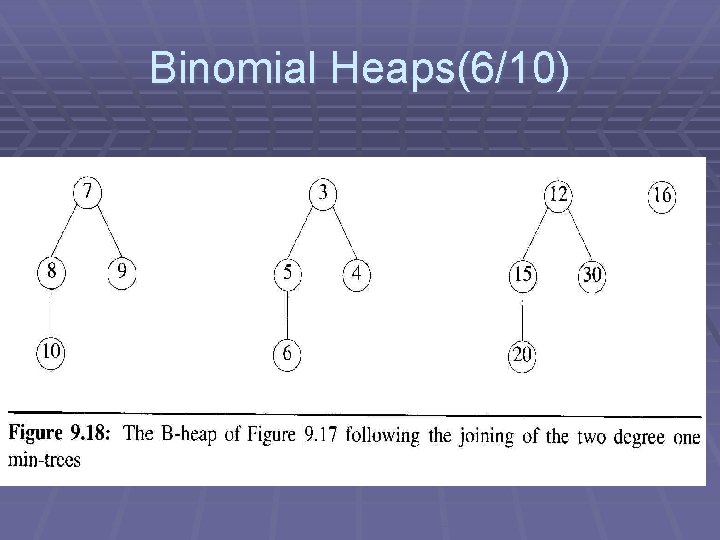
Binomial Heaps(7/10)

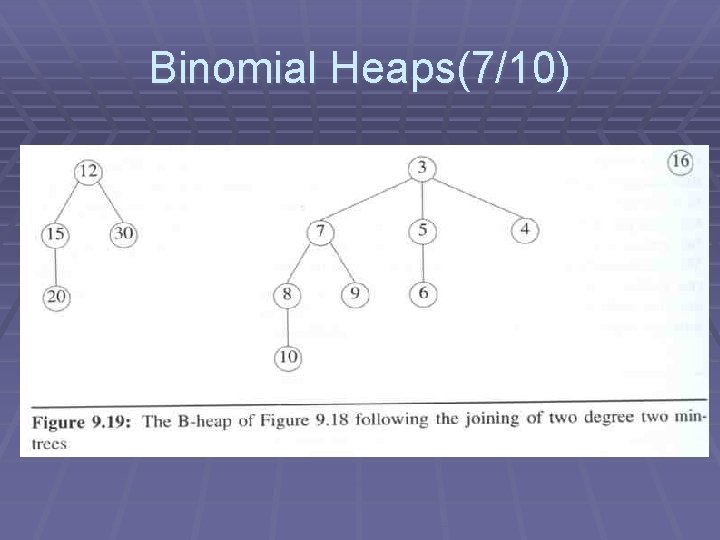
Binomial Heaps(8/10)

Binomial Heaps(9/10)

Binomial Heaps(10/10) § Trees in B-Heaps is Binomial tree § B 0 has exactly one node § Bk, k > 0, consists of a root with degree k and whose subtrees are B 0, B 1, …, Bk-1 § Bk has exactly 2 k nodes § actual cost of a delete is O(logn + s) § s = number of min-trees in a (original roots - 1) and y (children of the removed node)

Fibonacci Heaps(1/8) § Definition § delete, delete the element in a specified node § decrease key § This two operations are followed by cascading cut

Fibonacci Heaps(2/8) § Deletion From An F-heap § min or not min

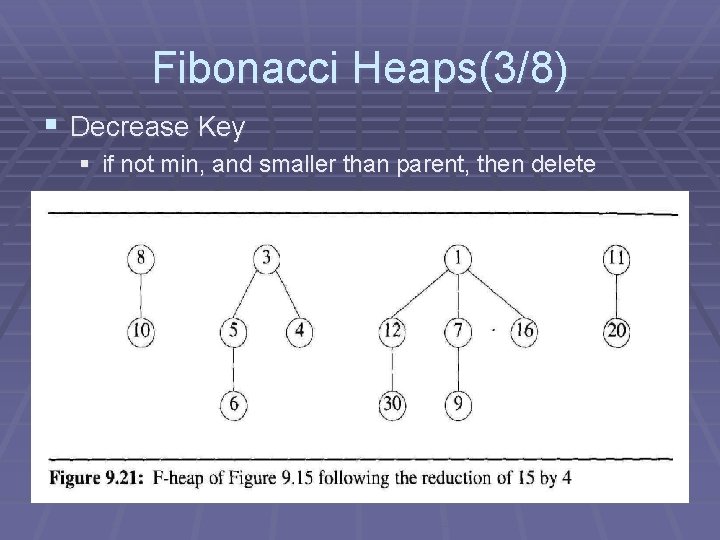
Fibonacci Heaps(3/8) § Decrease Key § if not min, and smaller than parent, then delete

Fibonacci Heap(4/8) § To prevent the amortized cost of delete min becomes O(n), each node can have only one child be deleted. § If two children of x were deleted, then x must be cut and moved to the ring of roots. § Using a flag (true of false) to indicate whether one of x’s child has been cut

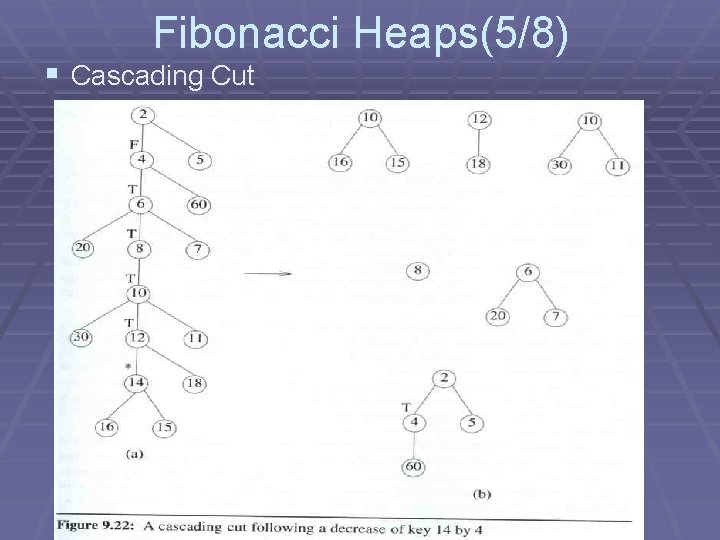
Fibonacci Heaps(5/8) § Cascading Cut

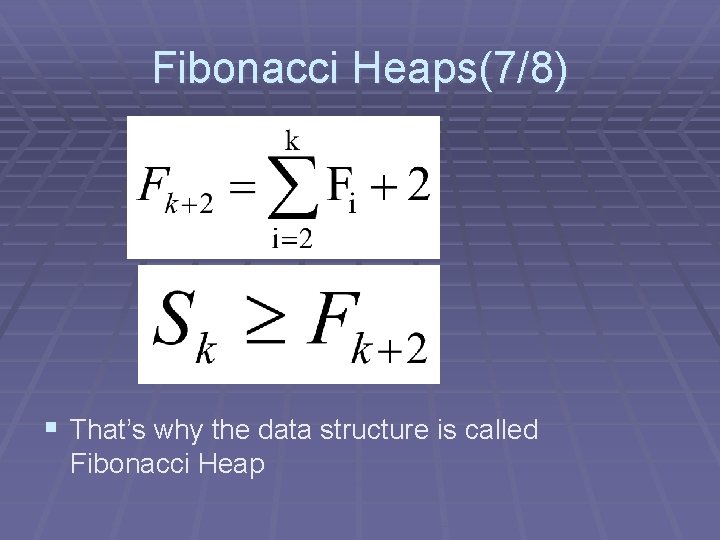
Fibonacci Heaps(6/8) § Lemma § the ith child of any node x in a F-Heap has a degree of at least i – 2, except when i=1 the degree is 0 § Corollary § Let Sk be the minimum possible number of descendants of a node of degree k, then S 0=1, S 1=2. From the lemma above, we got (2 comes from 1 st child and root)

Fibonacci Heaps(7/8) § That’s why the data structure is called Fibonacci Heap

Fibonacci Heaps(8/8) § Application Of F-heaps