CS 224 Computer Organization Spring 2011 Arithmetic for

CS 224 Computer Organization Spring 2011 Arithmetic for Computers With thanks to M. J. Irwin, D. Patterson, and J. Hennessy for some lecture slide contents

Numbers • Bits are just bits (no inherent meaning) — conventions define relationship between bits and numbers • Binary numbers (base 2) 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001. . . decimal: 0. . . 2 n-1 • Of course it gets more complicated: numbers are finite (overflow) fractions and real numbers negative numbers e. g. , no MIPS subi instruction; addi can add a negative number • How do we represent negative numbers? i. e. , which bit patterns will represent which numbers? CS 224 Spring 2010 Chapter 3 2

Number Representations • 32 -bit signed numbers (2’s complement): 0000 0000 two = 0 ten 0000 0000 0001 two = + 1 ten. . . 0111 1000. . . 1111 1111 0000 0000 1111 0000 1110 two 1111 two 0000 two 0001 two = = + + – – 2, 147, 483, 646 ten 2, 147, 483, 647 ten 2, 147, 483, 648 ten 2, 147, 483, 647 ten 1111 1111 1110 two = – 2 ten 1111 1111 two = – 1 ten • Converting <32 -bit values into 32 -bit values copy the most significant bit (the sign bit) into the “empty” bits 0010 -> 0000 0010 1010 -> 1111 1010 sign extend CS 224 Spring 2010 Chapter 3 versus zero extend (lb vs. lbu) 3

MIPS Arithmetic Logic Unit (ALU) • Must support the Arithmetic/Logic operations of the ISA -add, addiu, addu -sub, subu -mult, multu, divu -sqrt -and, andi, nor, ori, xori -beq, bne, slti, sltu, sltiu • With special handling for • sign extend – addi, addiu, sltiu • zero extend – andi, ori, xori • overflow detection – add, addi, sub CS 224 Spring 2010 Chapter 3 4

Dealing with Overflow occurs when the result of an operation cannot be represented in 32 -bits, i. e. , when the sign bit contains a value bit of the result and not the proper sign bit When adding operands with different signs or when subtracting operands with the same sign, overflow can never occur Operation Operand A Operand B Result indicating overflow A+B ≥ 0 <0 A+B <0 <0 ≥ 0 A-B ≥ 0 <0 <0 A-B <0 ≥ 0 MIPS signals overflow with an exception (a. k. a. interrupt) – an unscheduled procedure call to the OS, where the Exception Program Counter (EPC) contains the address of the instruction that caused the exception CS 224 Spring 2010 Chapter 3 5

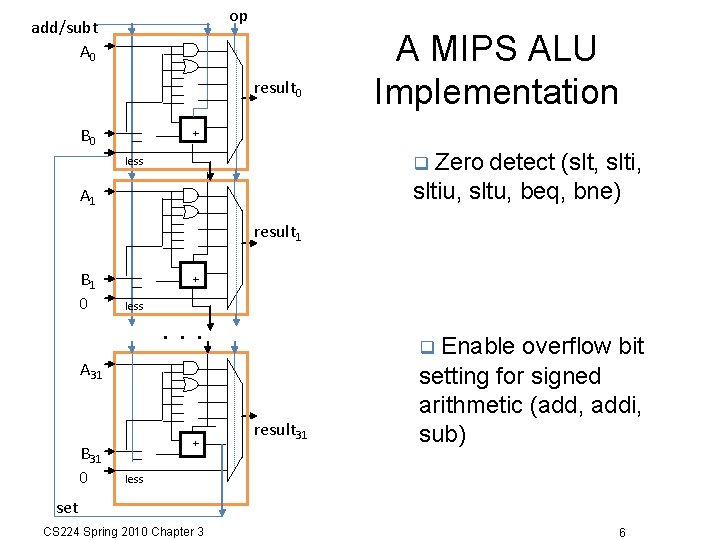
op add/subt A 0 result 0 B 0 A MIPS ALU Implementation + Zero detect (slt, sltiu, sltu, beq, bne) less A 1 result 1 B 1 0 + less . . . Enable A 31 B 31 0 + result 31 overflow bit setting for signed arithmetic (add, addi, sub) less set CS 224 Spring 2010 Chapter 3 6

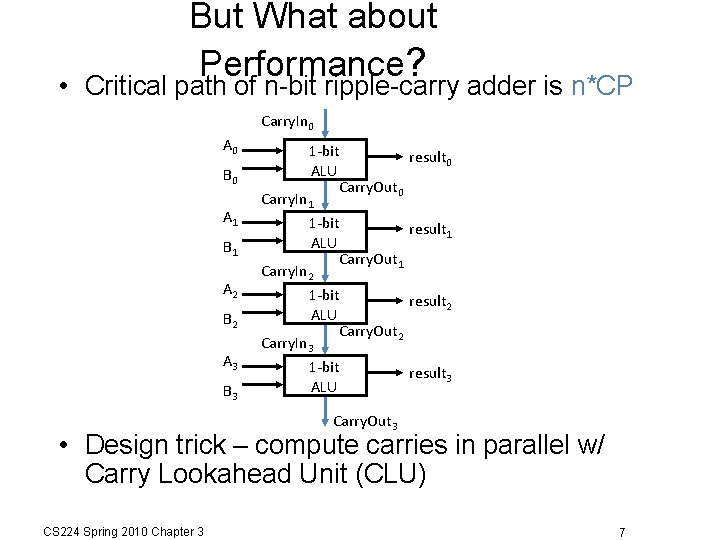
But What about Performance? • Critical path of n-bit ripple-carry adder is n*CP Carry. In 0 A 0 B 0 A 1 B 1 A 2 B 2 A 3 B 3 1 -bit result 0 ALU Carry. Out 0 Carry. In 1 1 -bit result 1 ALU Carry. Out 1 Carry. In 2 1 -bit result 2 ALU Carry. Out 2 Carry. In 3 1 -bit result 3 ALU Carry. Out 3 • Design trick – compute carries in parallel w/ Carry Lookahead Unit (CLU) CS 224 Spring 2010 Chapter 3 7

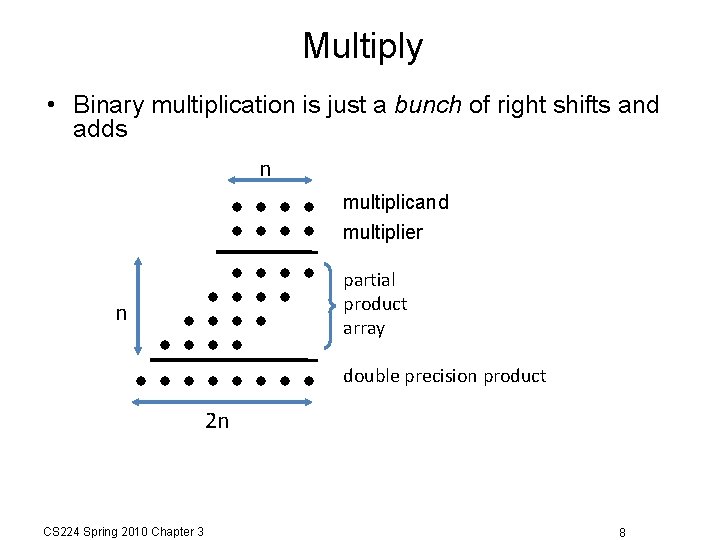
Multiply • Binary multiplication is just a bunch of right shifts and adds n multiplicand multiplier partial product array n double precision product 2 n CS 224 Spring 2010 Chapter 3 8

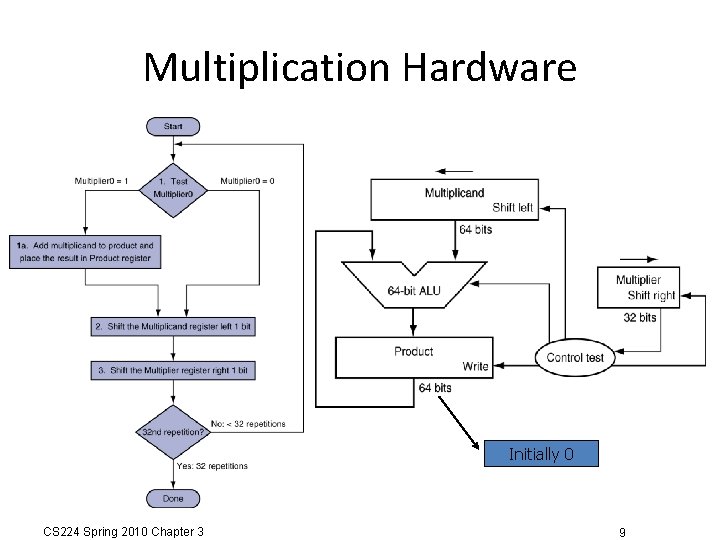
Multiplication Hardware Initially 0 CS 224 Spring 2010 Chapter 3 9

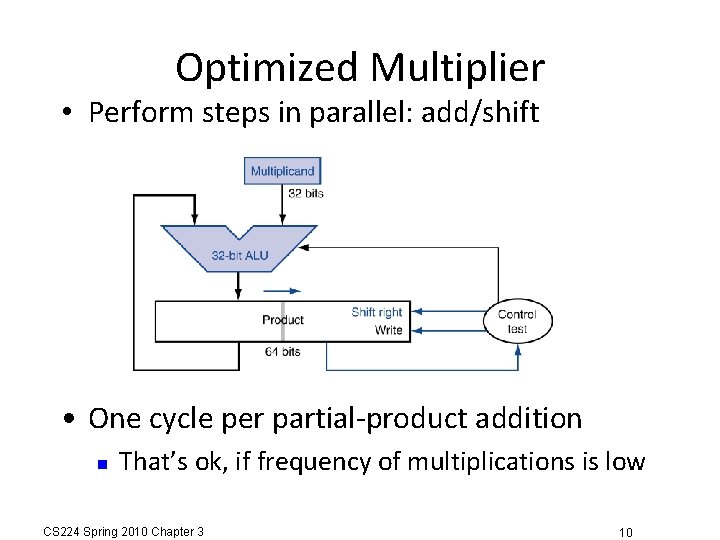
Optimized Multiplier • Perform steps in parallel: add/shift • One cycle per partial-product addition That’s ok, if frequency of multiplications is low CS 224 Spring 2010 Chapter 3 10

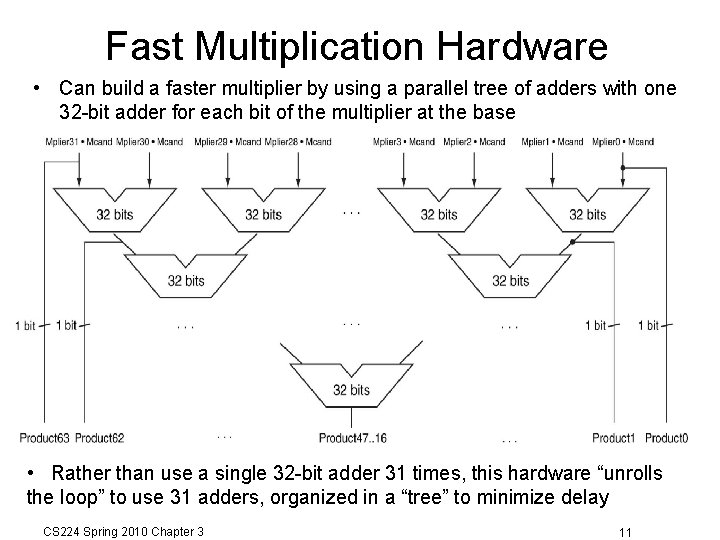
Fast Multiplication Hardware • Can build a faster multiplier by using a parallel tree of adders with one 32 -bit adder for each bit of the multiplier at the base • Rather than use a single 32 -bit adder 31 times, this hardware “unrolls the loop” to use 31 adders, organized in a “tree” to minimize delay CS 224 Spring 2010 Chapter 3 11

Multiply in MIPS • Product stored in two 32 -bit registers called Hi and Low mult $s 0, $s 1 multu $s 0, $s 1 # $s 0 * $s 1 -> high/low # $s 0 * $s 1 (unsigned) • Results are moved from Hi/Low mfhi $t 0 mflo $t 0 # $t 0 = Hi # $t 0 = Low • Pseudoinstruction mul $t 0, $s 1 CS 224 Spring 2010 Chapter 3 # $t 0 = $s 0 * $s 1 12

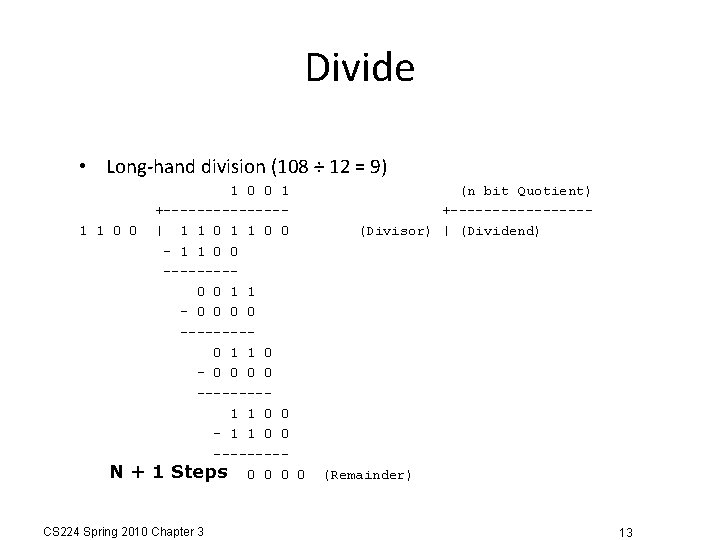
Divide • Long-hand division (108 ÷ 12 = 9) 1 1 0 0 N+ 1 0 0 1 +-------| 1 1 0 0 ----0 0 1 1 - 0 0 ----0 1 1 0 - 0 0 ----1 1 0 0 ----1 Steps 0 0 CS 224 Spring 2010 Chapter 3 (n bit Quotient) +--------(Divisor) | (Dividend) (Remainder) 13

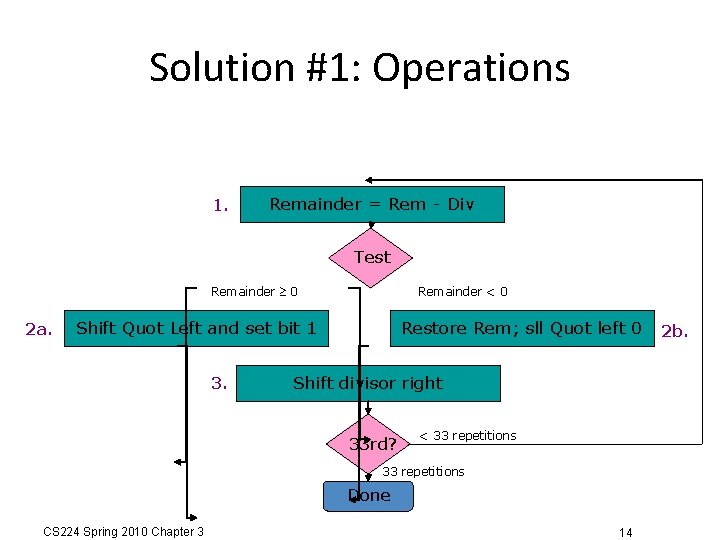
Solution #1: Operations 1. Remainder = Rem - Div Test Remainder 0 2 a. Remainder < 0 Shift Quot Left and set bit 1 3. Restore Rem; sll Quot left 0 Shift divisor right 33 rd? < 33 repetitions Done CS 224 Spring 2010 Chapter 3 14 2 b.

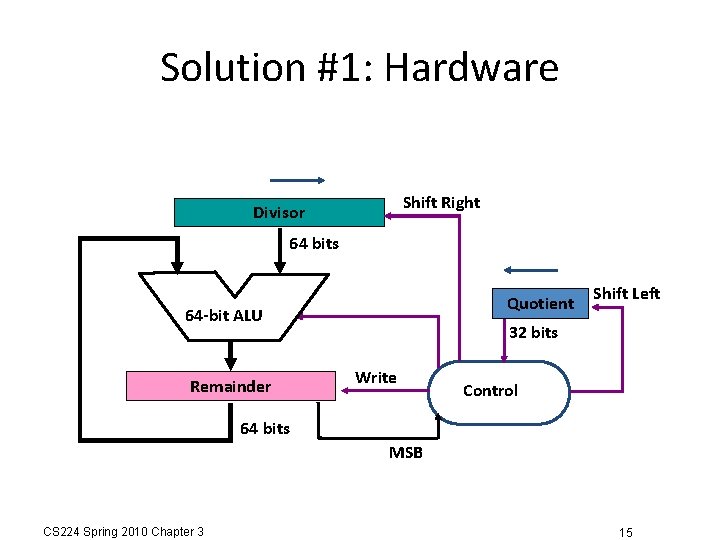
Solution #1: Hardware Shift Right Divisor 64 bits Quotient 64 -bit ALU Remainder Shift Left 32 bits Write Control 64 bits MSB CS 224 Spring 2010 Chapter 3 15

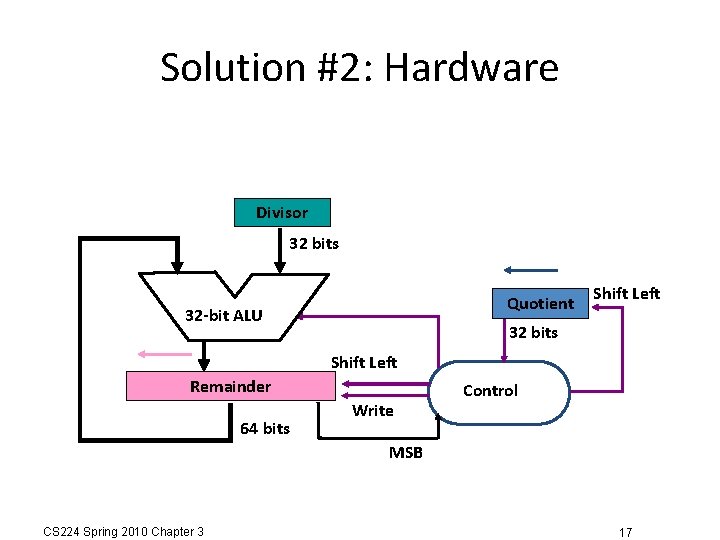
Issues and Alternative • Notice that: Half of the divisor bits are always 0 • Either high or low bits are 0, even as shifted Half of the 64 bit adder is therefore wasted • Solution #2 Instead of shifting divisor right, shift the remainder left Adder only needs to be 32 bits wide Can also remove an iteration by switching order to shift and then subtract Remainder is in left half of register CS 224 Spring 2010 Chapter 3 16

Solution #2: Hardware Divisor 32 bits Quotient 32 -bit ALU Shift Left 32 bits Shift Left Remainder 64 bits Write Control MSB CS 224 Spring 2010 Chapter 3 17

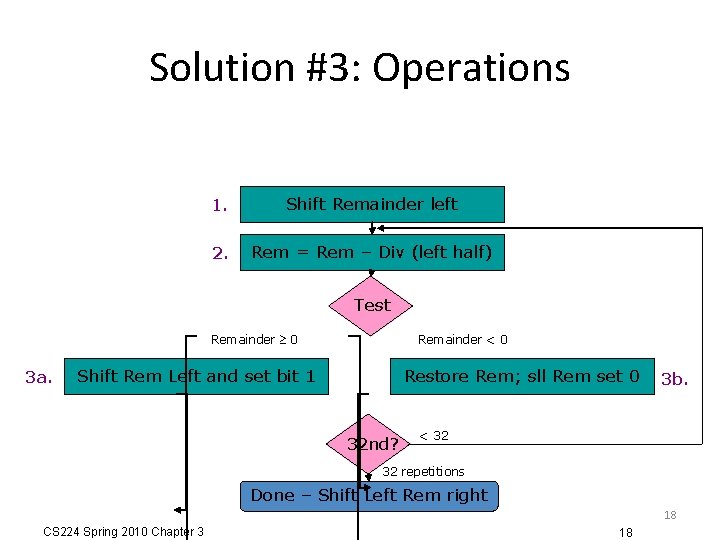
Solution #3: Operations 1. Shift Remainder left 2. Rem = Rem – Div (left half) Test Remainder 0 3 a. Remainder < 0 Shift Rem Left and set bit 1 Restore Rem; sll Rem set 0 32 nd? 3 b. < 32 32 repetitions Done – Shift Left Rem right 18 CS 224 Spring 2010 Chapter 3 18

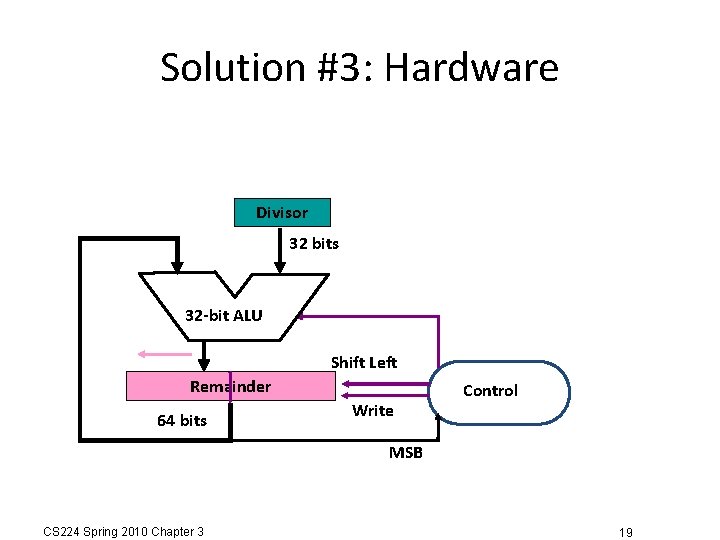
Solution #3: Hardware Divisor 32 bits 32 -bit ALU Shift Left Remainder 64 bits Write Control MSB CS 224 Spring 2010 Chapter 3 19

Divide in MIPS • Quotient and remainder stored in two 32 -bit registers called Hi and Low div $s 0, $s 1 divu $s 0, $s 1 # $s 0/$s 1 -> high/low # $s 0/$s 1 (unsigned) • Results are moved from Hi/Low mfhi $t 0 mflo $t 0 # $t 0 = Hi (remainder) # $t 0 = Low (quotient) • Pseudoinstructions div $t 0, $s 1 rem $t 0, $s 1 CS 224 Spring 2010 Chapter 3 # $t 0 = $s 0 / $s 1 # $t 0 = $s 0 % $s 1 20

§ 3. 5 Floating Point • Representation for non-integer numbers Including very small and very large numbers • Like scientific notation – 2. 34 × 1056 +0. 002 × 10– 4 +987. 02 × 109 normalized not normalized • In binary ± 1. xxxxxxx 2 × 2 yyyy • Types float and double in C CS 224 Spring 2010 Chapter 3 21

Floating Point Standard • Defined by IEEE Std 754 -1985 • Developed in response to divergence of representations Portability issues for scientific code • Now almost universally adopted • Two representations Single precision (32 -bit) Double precision (64 -bit) CS 224 Spring 2010 Chapter 3 22

IEEE Floating-Point Format single: 8 bits double: 11 bits S Exponent single: 23 bits double: 52 bits Fraction • S: sign bit (0 non-negative, 1 negative) • Normalize significand: 1. 0 ≤ |significand| < 2. 0 Always has a leading pre-binary-point 1 bit, so no need to represent it explicitly (hidden bit) Significand is Fraction with the “ 1. ” restored • Exponent: excess representation: actual exponent + Bias Ensures exponent is unsigned Single: Bias = 127; Double: Bias = 1023 CS 224 Spring 2010 Chapter 3 23

Single-Precision Range • Exponents 0000 and 1111 reserved • Smallest value Exponent: 00000001 actual exponent = 1 – 127 = – 126 Fraction: 000… 00 significand = 1. 0 ± 1. 0 × 2– 126 ≈ ± 1. 2 × 10– 38 • Largest value exponent: 11111110 actual exponent = 254 – 127 = +127 Fraction: 111… 11 significand ≈ 2. 0 ± 2. 0 × 2+127 ≈ ± 3. 4 × 10+38 CS 224 Spring 2010 Chapter 3 24

IEEE 754 Double Precision • Double precision number represented in 64 bits • MIPS Format Exponent: bias 1023 binary integer 0 < E < 2047 11 sign 1 S E (-1)S × 2 E Significand: magnitude, normalized binary significand with hidden bit (1): 1. F 20 F F 32 or (-1)S × (1 + Fraction) × 2(Exponent-Bias) CS 224 Spring 2010 Chapter 3 25

Double-Precision Range • Exponents 0000… 00 and 1111… 11 reserved • Smallest value Exponent: 000001 actual exponent = 1 – 1023 = – 1022 Fraction: 000… 00 significand = 1. 0 ± 1. 0 × 2– 1022 ≈ ± 2. 2 × 10– 308 • Largest value Exponent: 111110 actual exponent = 2046 – 1023 = +1023 Fraction: 111… 11 significand ≈ 2. 0 ± 2. 0 × 2+1023 ≈ ± 1. 8 × 10+308 CS 224 Spring 2010 Chapter 3 26

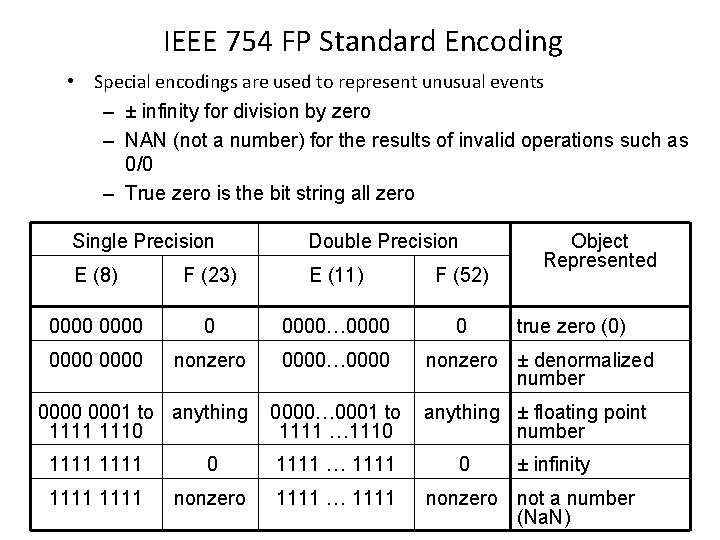
IEEE 754 FP Standard Encoding • Special encodings are used to represent unusual events – ± infinity for division by zero – NAN (not a number) for the results of invalid operations such as 0/0 – True zero is the bit string all zero Single Precision Double Precision E (8) F (23) E (11) F (52) 0000 0 0000… 0000 nonzero 0000… 0000 nonzero ± denormalized number 0000… 0001 to 1111 … 1110 anything ± floating point number 0000 0001 to anything 1111 1110 1111 … 1111 nonzero 1111 … 1111 0 Object Represented true zero (0) ± infinity nonzero not a number (Na. N)

Floating-Point Precision • Relative precision all fraction bits are significant Single: approx 2– 23 • Equivalent to 23 × log 102 ≈ 23 × 0. 3 ≈ 6 decimal digits of precision Double: approx 2– 52 • Equivalent to 52 × log 102 ≈ 52 × 0. 3 ≈ 16 decimal digits of precision CS 224 Spring 2010 Chapter 3 28

Floating-Point Example • What number is represented by the singleprecision float 11000000101000… 00 S=1 Fraction = 01000… 002 Exponent = 100000012 = 129 • x = (– 1)1 × (1 +. 012) × 2(129 – 127) = (– 1) × 1. 25 × 22 = – 5. 0 CS 224 Spring 2010 Chapter 3 29

Floating-Point Addition • Consider a 4 -digit decimal example 9. 999 × 101 + 1. 610 × 10– 1 • 1. Align decimal points Shift number with smaller exponent 9. 999 × 101 + 0. 016 × 101 • 2. Add significands 9. 999 × 101 + 0. 016 × 101 = 10. 015 × 101 • 3. Normalize result & check for over/underflow 1. 0015 × 102 • 4. Round and renormalize if necessary 1. 002 × 102 CS 224 Spring 2010 Chapter 3 30

Floating-Point Addition • Now consider a 4 -digit binary example – 1 + – 1. 110 × 2– 2 (0. 5 + – 0. 4375) 1. 0002 × 2 2 • 1. Align binary points Shift number with smaller exponent – 1 + – 0. 111 × 2– 1 1. 0002 × 2 2 • 2. Add significands – 1 + – 0. 111 × 2– 1 = 0. 001 × 2– 1 1. 0002 × 2 2 2 • 3. Normalize result & check for over/underflow – 4 1. 0002 × 2 , with no over/underflow • 4. Round and renormalize if necessary – 4 (no change) = 0. 0625 1. 0002 × 2 CS 224 Spring 2010 Chapter 3 31

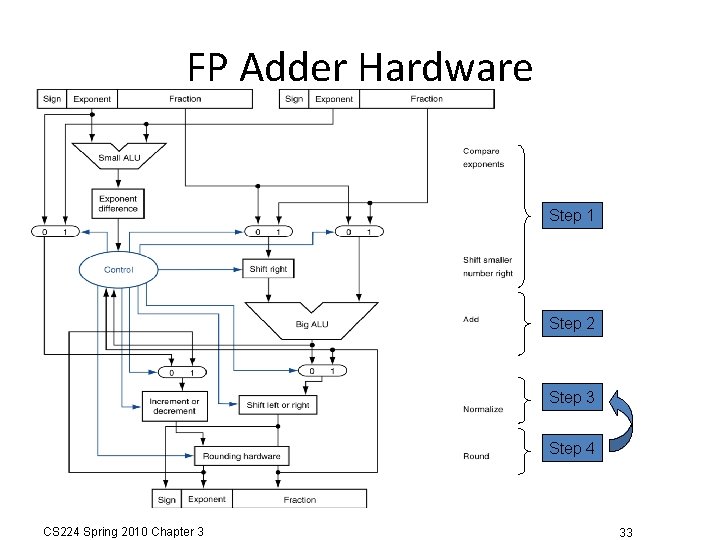
FP Adder Hardware • Much more complex than integer adder • Doing it in one clock cycle would take too long – Much longer than integer operations – Slower clock would penalize all instructions • FP adder usually takes several cycles – Can be pipelined CS 224 Spring 2010 Chapter 3 32

FP Adder Hardware Step 1 Step 2 Step 3 Step 4 CS 224 Spring 2010 Chapter 3 33

FP Arithmetic Hardware • FP multiplier is of similar complexity to FP adder o But uses a multiplier for significands instead of an adder • FP arithmetic hardware usually does Addition, subtraction, multiplication, division, reciprocal, square-root o FP integer conversion o • Operations usually takes several cycles o Can be pipelined CS 224 Spring 2010 Chapter 3 36

FP Instructions in MIPS • FP hardware is coprocessor 1 o Adjunct processor that extends the ISA • Separate FP registers o o 32 single-precision: $f 0, $f 1, … $f 31 Paired for double-precision: $f 0/$f 1, $f 2/$f 3, … • Release 2 of MIPs ISA supports 32 × 64 -bit FP reg’s • FP instructions operate only on FP registers Programs generally don’t do integer ops on FP data, or vice versa o Gives us more registers w/ minimal code-size impact o • FP load and store instructions o lwc 1, ldc 1, swc 1, sdc 1 • e. g. , ldc 1 $f 8, 32($sp) CS 224 Spring 2010 Chapter 3 37

FP Instructions in MIPS • Single-precision arithmetic add. s, sub. s, mul. s, div. s • e. g. : add. s $f 0, $f 1, $f 6 • Double-precision arithmetic add. d, sub. d, mul. d, div. d • e. g. : mul. d $f 4, $f 6 • Single- and double-precision comparison c. xx. s, c. xx. d (xx is eq, lt, le, …) Sets or clears FP condition-code bit • e. g. : c. lt. s $f 3, $f 4 • Branch on FP condition code true or false bc 1 t, bc 1 f • e. g. : bc 1 t Target. Label CS 224 Spring 2010 Chapter 3 38

FP Example: °F to °C • C code: float f 2 c (float fahr) { return ((5. 0/9. 0)*(fahr - 32. 0)); } fahr in $f 12, result in $f 0, literals in global memory space • Compiled MIPS code: f 2 c: lwc 1 div. s lwc 1 sub. s mul. s jr CS 224 Spring 2010 Chapter 3 $f 16, $f 18, $f 0, $ra const 5($gp) const 9($gp) $f 16, $f 18 const 32($gp) $f 12, $f 18 $f 16, $f 18 39

§ 3. 6 Parallelism and Computer Arithmetic: Associativity • Parallel programs may interleave operations in unexpected orders • Assumptions of associativity may fail, since FP operations are not associative ! • Need to validate parallel programs under varying degrees of parallelism CS 224 Spring 2010 Chapter 3 40

Support for Accurate Arithmetic • IEEE 754 FP rounding modes • • Always round up (toward +∞) Always round down (toward -∞) Truncate (toward 0) Round to nearest even (when the Guard || Round || Sticky are 100) – always creates a 0 in the least significant (kept) bit of F • Rounding (except for truncation) requires the hardware to include extra F bits during calculations • Guard bit – used to provide one F bit when shifting left to normalize a result (e. g. , when normalizing F after division or subtraction) G • Round bit – used to improve rounding accuracy R • Sticky bit – used to support Round to nearest even; is set to a 1 whenever a 1 bit shifts (right) through it (e. g. , when aligning F during addition/subtraction) S F = 1. xxxxxxxxxxxx G R S CS 224 Spring 2010 Chapter 3 41