CS 222 LECTURE 03 PROGRAMMING LANGUAGES Finite Automata

CS 222 LECTURE 03 PROGRAMMING LANGUAGES

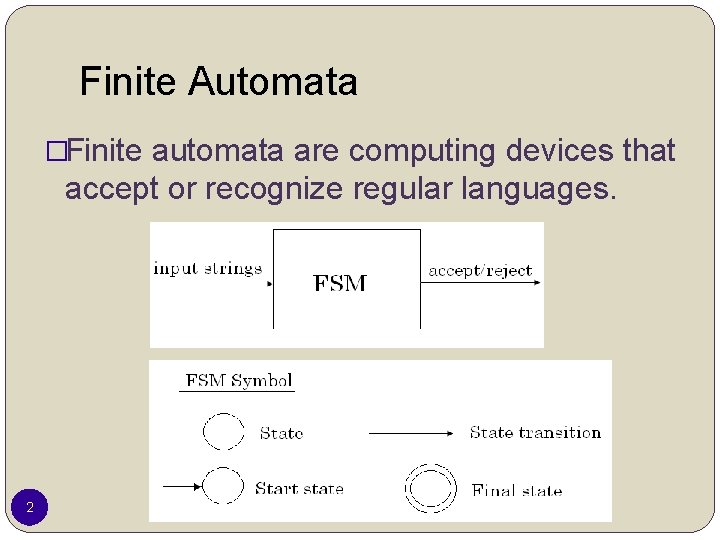
Finite Automata �Finite automata are computing devices that accept or recognize regular languages. 2

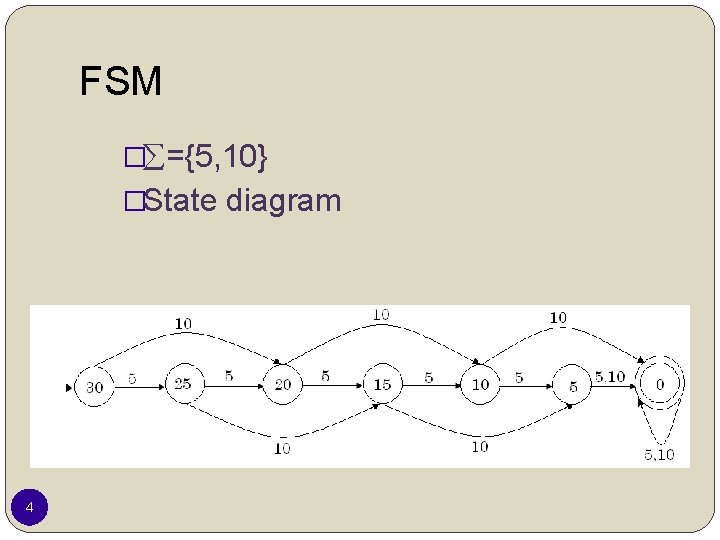
Finite state machine �Let think about a soda vending machine which accept only 5 and 10 Baht coin. �A soda bottle cost 30 Baht. �Now we have 7 states to put the coin. �Start state need 30 Baht, next state need 25, 20, 15, 10, 5, and a final state need 0 Baht. �Let draw a state diagram for the machine 3

FSM � ={5, 10} �State diagram 4

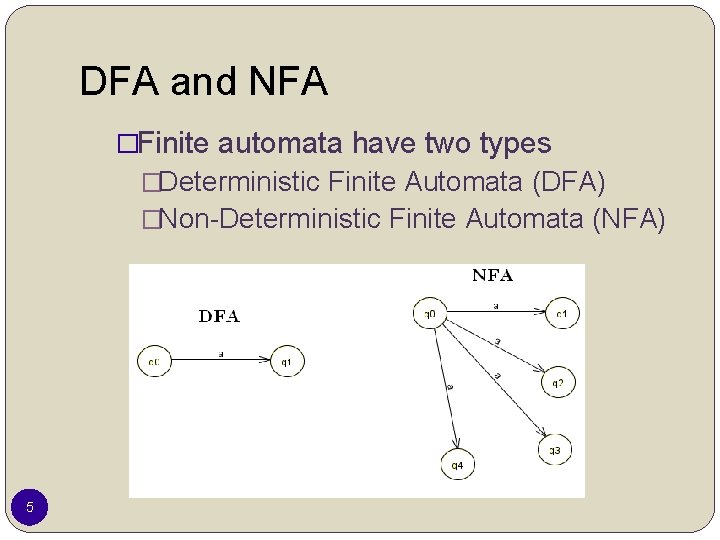
DFA and NFA �Finite automata have two types �Deterministic Finite Automata (DFA) �Non-Deterministic Finite Automata (NFA) 5

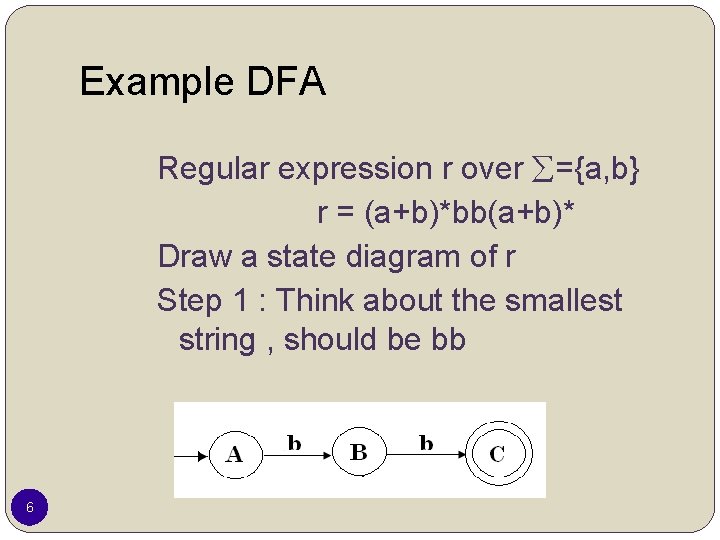
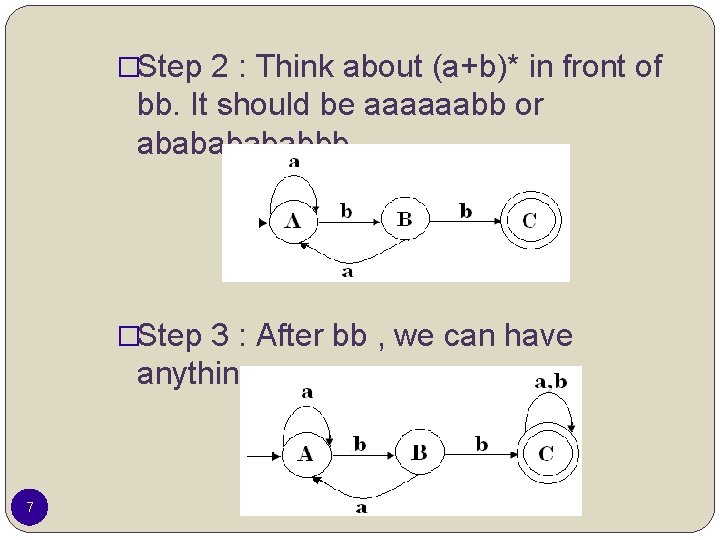
Example DFA Regular expression r over ={a, b} r = (a+b)*bb(a+b)* Draw a state diagram of r Step 1 : Think about the smallest string , should be bb 6

�Step 2 : Think about (a+b)* in front of bb. It should be aaaaaabb or abababbb �Step 3 : After bb , we can have anything. 7

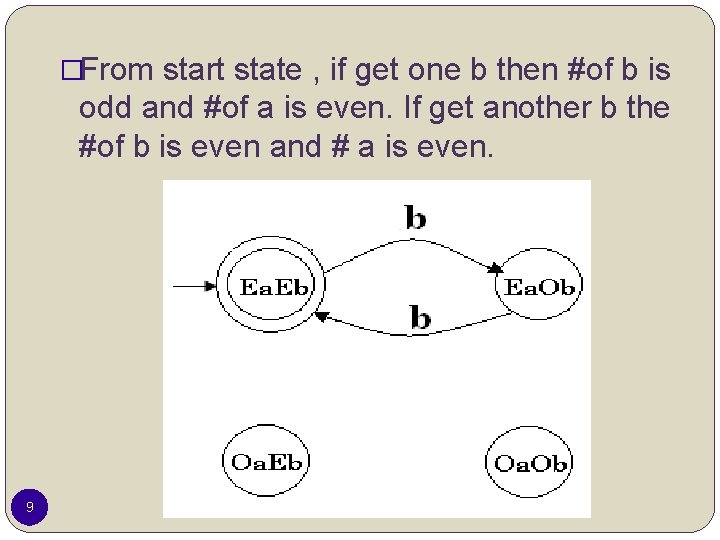
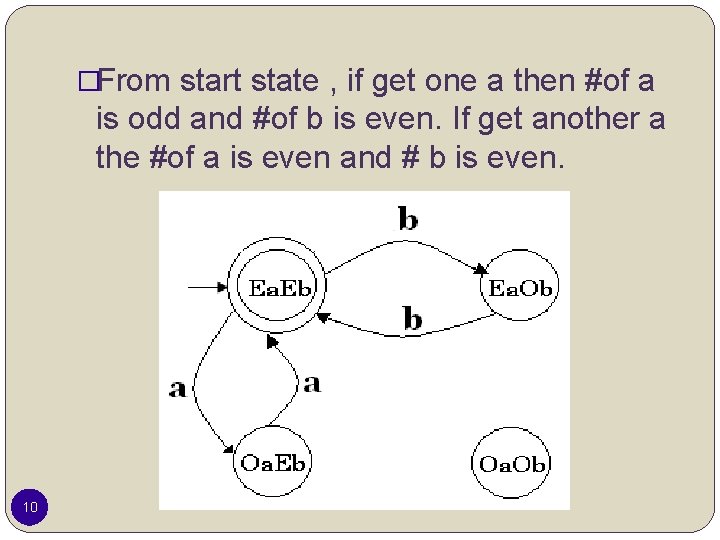
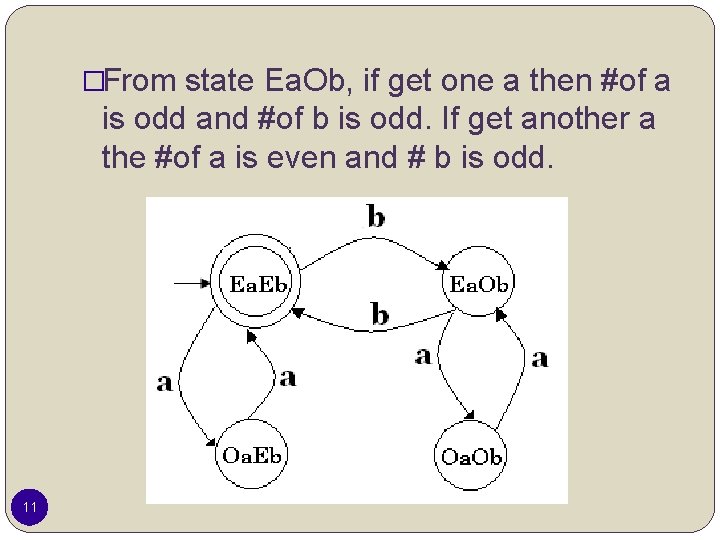
Example �L is a language over ={a, b} which have the even number of a and even number of b �Step 1: is in L, aa, bb, abab, aabb, aaaabb, aabbaa … are in L. We should have 4 states. 1) # of a and # of b is even 2) # of a is even and # of b is odd 3) # of a is odd and # of b is even 4) # of a is odd and # of b is odd 8

�From start state , if get one b then #of b is odd and #of a is even. If get another b the #of b is even and # a is even. 9

�From start state , if get one a then #of a is odd and #of b is even. If get another a the #of a is even and # b is even. 10

�From state Ea. Ob, if get one a then #of a is odd and #of b is odd. If get another a the #of a is even and # b is odd. 11

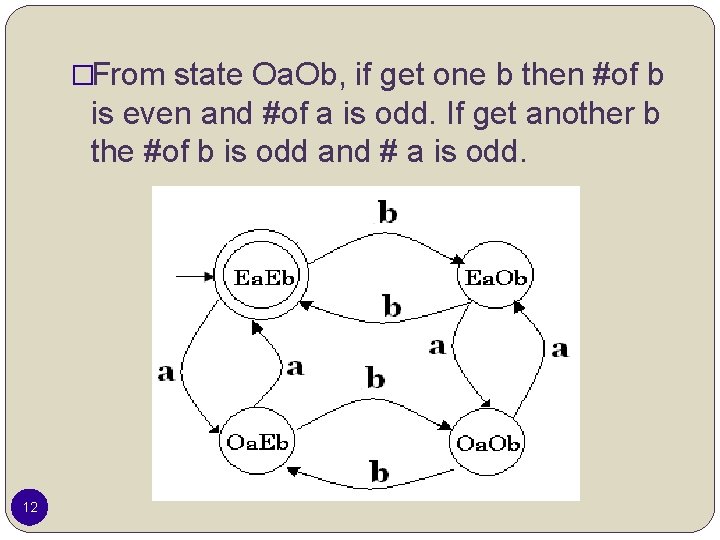
�From state Oa. Ob, if get one b then #of b is even and #of a is odd. If get another b the #of b is odd and # a is odd. 12

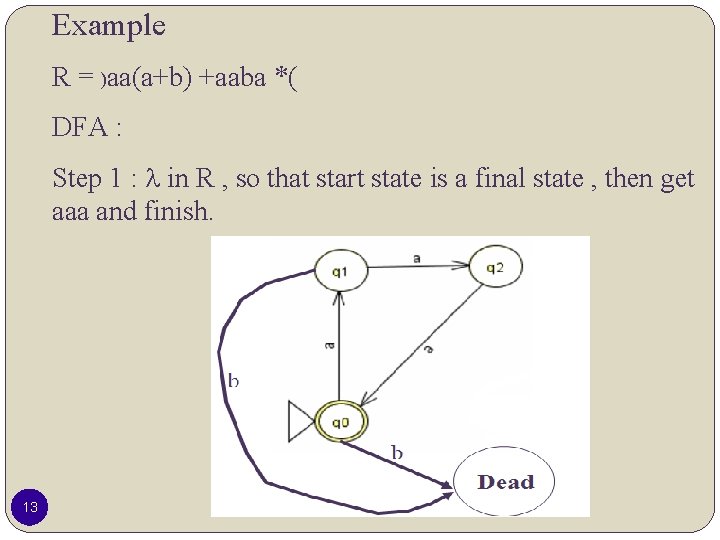
Example R = )aa(a+b) +aaba *( DFA : Step 1 : in R , so that start state is a final state , then get aaa and finish. 13

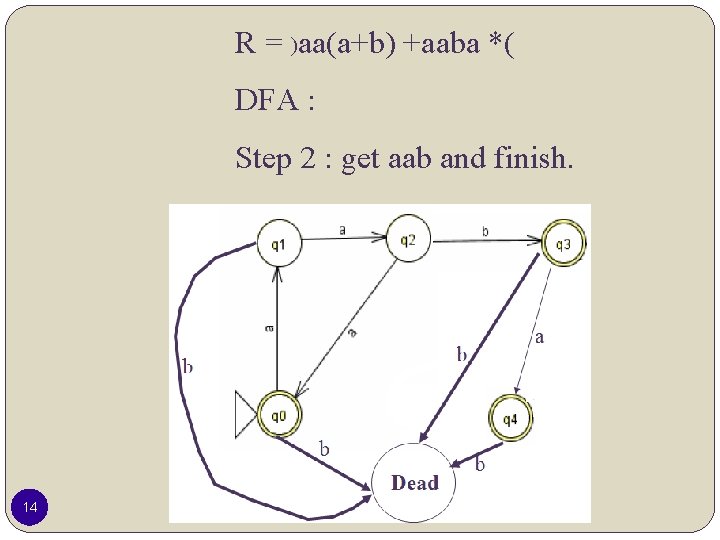
R = )aa(a+b) +aaba *( DFA : Step 2 : get aab and finish. 14

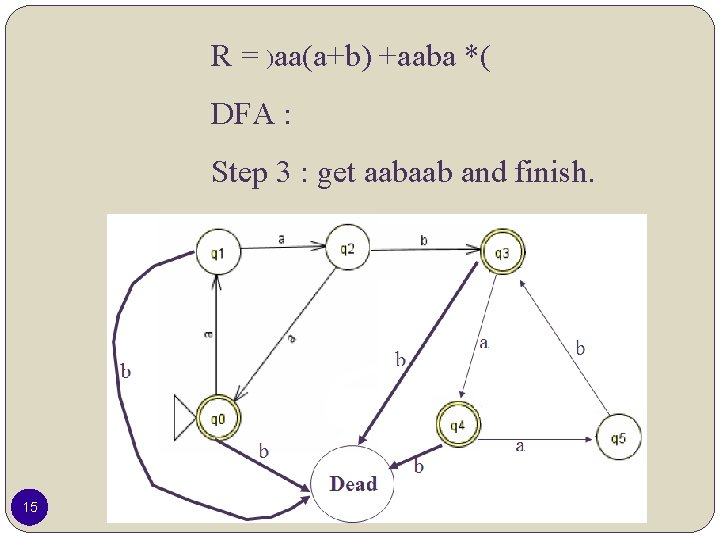
R = )aa(a+b) +aaba *( DFA : Step 3 : get aabaab and finish. 15

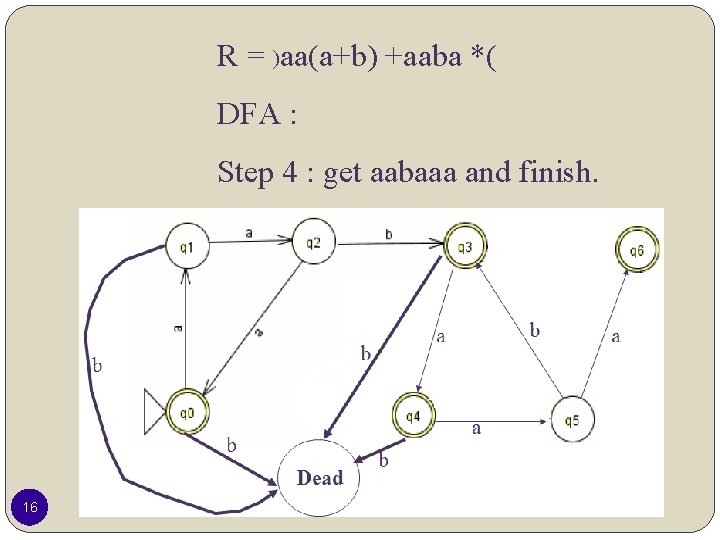
R = )aa(a+b) +aaba *( DFA : Step 4 : get aabaaa and finish. 16

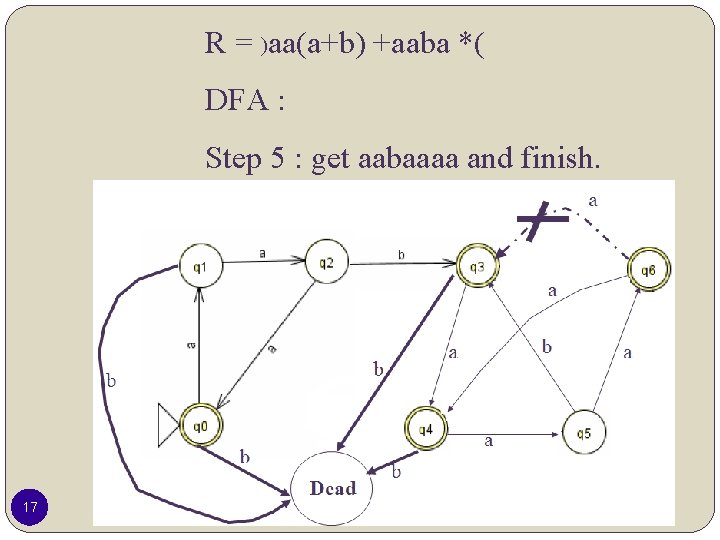
R = )aa(a+b) +aaba *( DFA : Step 5 : get aabaaaa and finish. 17

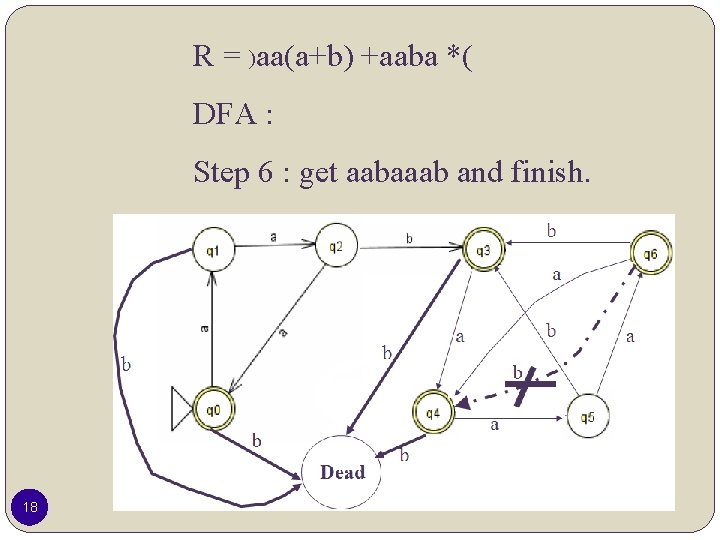
R = )aa(a+b) +aaba *( DFA : Step 6 : get aabaaab and finish. 18

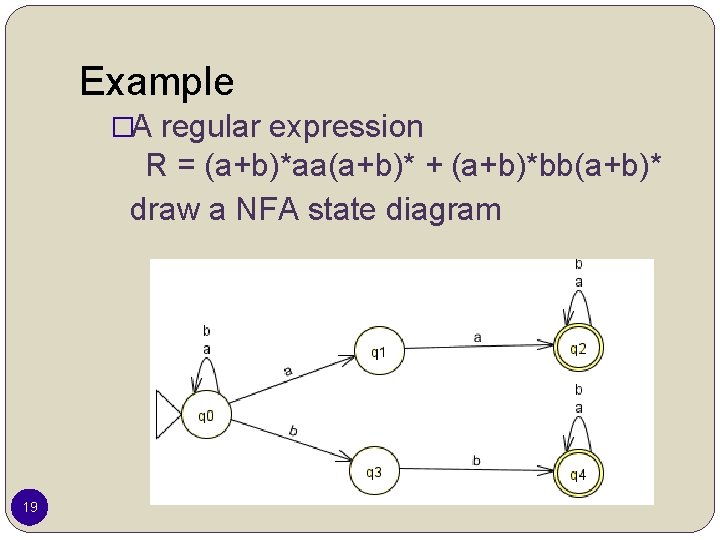
Example �A regular expression R = (a+b)*aa(a+b)* + (a+b)*bb(a+b)* draw a NFA state diagram 19

Try this �Draw a DFA state diagram from the given regular expression �R 1 �R 2 �R 3 �R 4 �R 5 �R 6 �R 7 �R 8 20 = (aa(a+b)*+(a+b)*bb) = (a+b)*bb(a+b)* = (a+b)*b(a+b)* = a(a+b)*b(a+b)*a = (a+b+c)*bc(a+b+c)* = (aa+ab+ba+bb)*(a+b) = (1+01)*

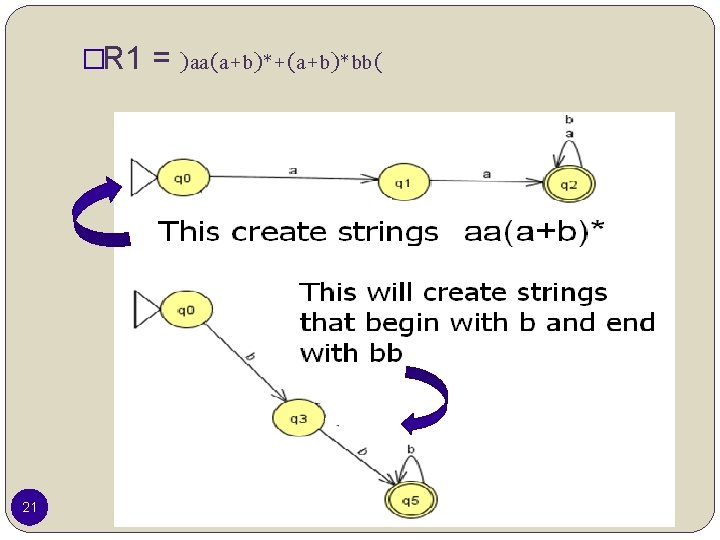
�R 1 = )aa(a+b)*+(a+b)*bb( 21

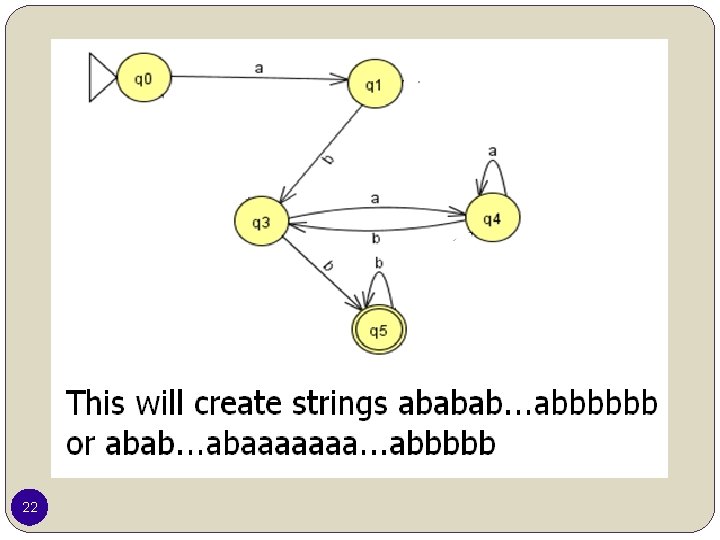
22

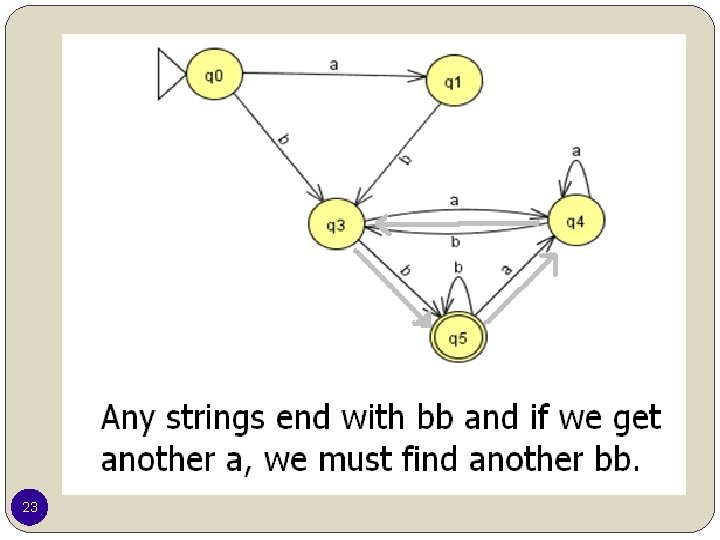
23

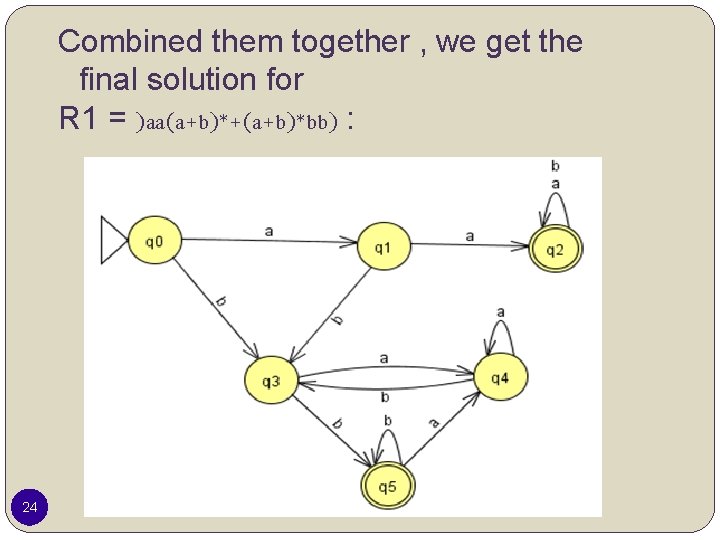
Combined them together , we get the final solution for R 1 = )aa(a+b)*+(a+b)*bb) : 24