CS 213 Floating Point Topics n n 1

CS 213 Floating Point Topics n n – 1 – IEEE Floating Point Standard Rounding Floating Point Operations Mathematical properties CS 213, F’ 06

Floating Point Puzzles n For each of the following C expressions, either: l Argue that it is true for all argument values l Explain why not true • x == (int)(float) x int x = …; • x == (int)(double) x float f = …; • f == (float)(double) f double d = …; • d == (float) d • f == -(-f); Assume neither d nor f is Na. N • 2/3 == 2/3. 0 • d < 0. 0 ((d*2) < 0. 0) • d > f -f > -d • d * d >= 0. 0 • (d+f)-d == f – 2 – CS 213, F’ 06

IEEE Floating Point Representations n Encodes rational numbers of the form V=x*(2^y) n Useful for very large numbers or numbers close to zero IEEE Standard 754 n Established in 1985 as uniform standard for floating point arithmetic l Before that, many idiosyncratic formats n Supported by all major CPUs Driven by Numerical Concerns n n Nice standards for rounding, overflow, underflow Hard to make go fast l Numerical analysts predominated over hardware types in defining standard – 3 – CS 213, F’ 06

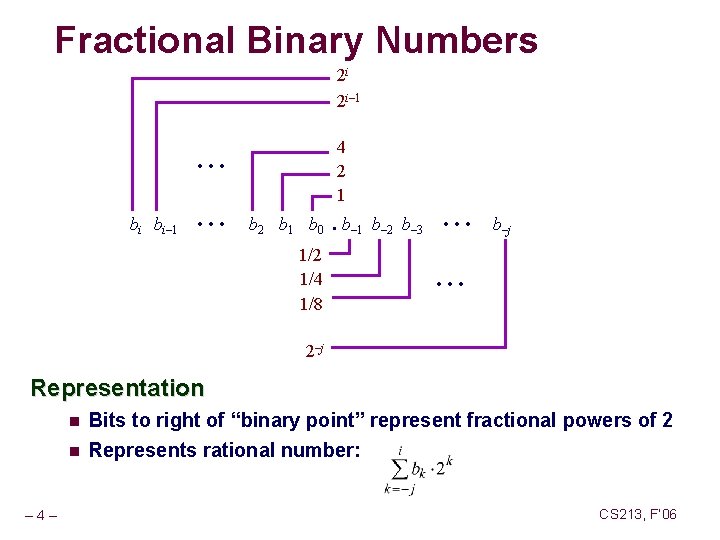
Fractional Binary Numbers 2 i 2 i– 1 4 2 1 bi bi– 1 • • • b 2 b 1 b 0. b– 1 b– 2 b– 3 1/2 1/4 1/8 • • • b–j • • • 2–j Representation – 4 – n Bits to right of “binary point” represent fractional powers of 2 n Represents rational number: CS 213, F’ 06

Frac. Binary Number Examples Value 5 -3/4 2 -7/8 63/64 Representation 101. 112 10. 1112 0. 1111112 Observations Divide by 2 by shifting right (the point moves to the left) n Multiply by 2 by shifting left (the point moves to the right) n Numbers of form 0. 111111… 2 just below 1. 0 n l 1/2 + 1/4 + 1/8 + … + 1/2 i + … 1. 0 l Use notation 1. 0 – – 5 – CS 213, F’ 06

Representable Numbers Limitation Can only exactly represent numbers of the form x/2 k n Other numbers have repeating bit representations n Value 1/3 1/5 1/10 – 6 – Representation 0. 010101[01]… 2 0. 00110011[0011]… 2 0. 000110011[0011]… 2 CS 213, F’ 06

Floating Point Representation Numerical Form n – 1 s M 2 E l Sign bit s determines whether number is negative or positive l Significand M normally a fractional value in range [1. 0, 2. 0). l Exponent E weights value by power of two Encoding s exp frac MSB is sign bit n exp field encodes E n frac field encodes M n – 7 – CS 213, F’ 06

Floating Point Precisions Encoding s exp frac MSB is sign bit n exp field encodes E n frac field encodes M n Sizes n Single precision: 8 exp bits, 23 frac bits l 32 bits total n Double precision: 11 exp bits, 52 frac bits l 64 bits total n Extended precision: 15 exp bits, 63 frac bits l Only found in Intel-compatible machines l Stored in 80 bits » 1 bit wasted – 8 – CS 213, F’ 06

Three Cases of Floating Point Representations Normalized values n Most common cases Denomralized values Special values – 9 – CS 213, F’ 06

“Normalized” Numeric Values Condition n exp 000… 0 and exp 111… 1 Exponent coded as biased value E = Exp – Bias l Exp : unsigned value denoted by exp l Bias : Bias value » Single precision: 127 (Exp: 1… 254, E: -126… 127) » Double precision: 1023 (Exp: 1… 2046, E: -1022… 1023) » in general: Bias = 2 e-1 - 1, where e is number of exponent bits Significand coded with implied leading 1 M = 1. xxx…x 2 l xxx…x: bits of frac l Minimum when 000… 0 (M = 1. 0) l Maximum when 111… 1 (M = 2. 0 – ) l Get extra leading bit for “free” – 10 – CS 213, F’ 06

Normalized Encoding Example Value Float F = 15213. 0; n 1521310 = 111011012 = 1. 11011012 X 213 Significand M = frac = 1. 11011012 1101101000002 Exponent E = Bias = Exp = 13 127 140 = 100011002 Floating Point Representation: Hex: Binary: 140: 15213: – 11 – 4 6 6 D B 4 0 0 0100 0110 1101 1011 0100 0000 100 0110 0 1101 1011 01 CS 213, F’ 06

Denormalized Values Condition n exp = 000… 0 Value n Exponent value E = –Bias + 1 l Note: not simply E= – Bias n Significand value M = 0. xxx…x 2 l xxx…x: bits of frac Cases n exp = 000… 0, frac = 000… 0 l Represents value 0 l Note that have distinct values +0 and – 0 n exp = 000… 0, frac 000… 0 l Numbers very close to 0. 0 – 12 – CS 213, F’ 06

Special Values Condition n exp = 111… 1 Cases n exp = 111… 1, frac = 000… 0 l Represents value (infinity) l Operation that overflows l Both positive and negative l E. g. , 1. 0/0. 0 = 1. 0/ 0. 0 = + , 1. 0/ 0. 0 = n exp = 111… 1, frac 000… 0 l Not-a-Number (Na. N) l Represents case when no numeric value can be determined l E. g. , sqrt(– 1), – 13 – CS 213, F’ 06

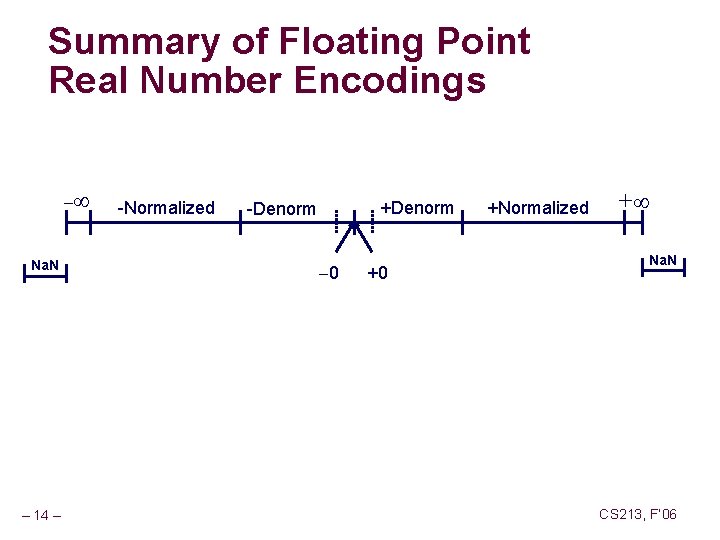
Summary of Floating Point Real Number Encodings Na. N – 14 – -Normalized +Denorm -Denorm 0 +0 +Normalized + Na. N CS 213, F’ 06

Tiny Floating Point Example 8 -bit Floating Point Representation n the sign bit is in the most significant bit. n the next four bits are the exponent, with a bias of 7. the last three bits are the frac n l Same General Form as IEEE Format n n normalized, denormalized representation of 0, Na. N, infinity 7 6 s – 15 – 0 3 2 exp frac CS 213, F’ 06

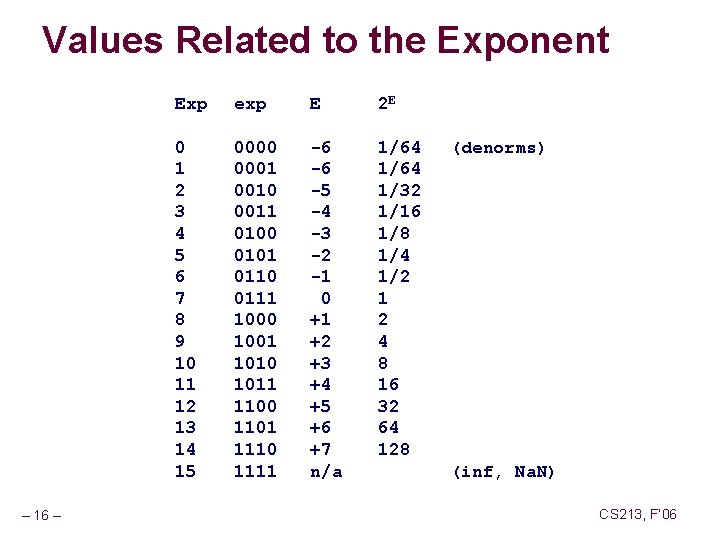
Values Related to the Exponent – 16 – Exp exp E 2 E 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 -6 -6 -5 -4 -3 -2 -1 0 +1 +2 +3 +4 +5 +6 +7 n/a 1/64 1/32 1/16 1/8 1/4 1/2 1 2 4 8 16 32 64 128 (denorms) (inf, Na. N) CS 213, F’ 06

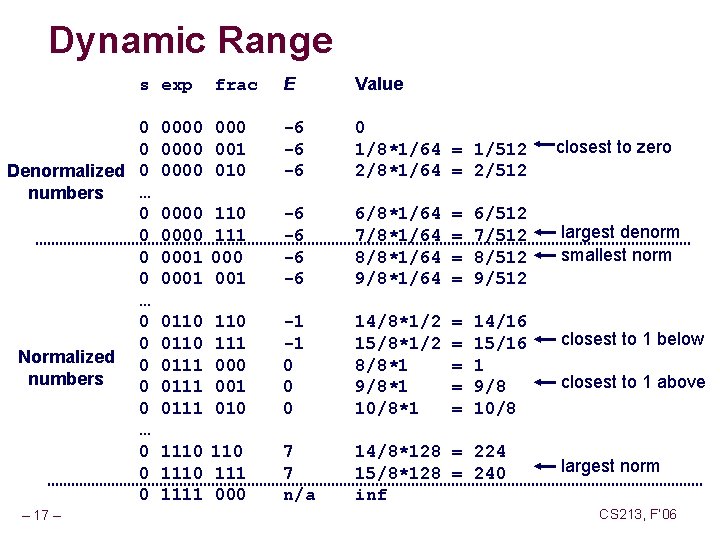
Dynamic Range E Value 0000 001 0000 010 -6 -6 -6 0 1/8*1/64 = 1/512 2/8*1/64 = 2/512 closest to zero 0000 0001 110 111 000 001 -6 -6 6/8*1/64 7/8*1/64 8/8*1/64 9/8*1/64 = = 6/512 7/512 8/512 9/512 largest denorm smallest norm 0110 0111 110 111 000 001 010 -1 -1 0 0 0 14/8*1/2 15/8*1/2 8/8*1 9/8*1 10/8*1 = = = 14/16 15/16 1 9/8 10/8 7 7 n/a 14/8*128 = 224 15/8*128 = 240 inf s exp 0 0 Denormalized 0 … numbers 0 0 … 0 0 Normalized 0 numbers 0 0 … 0 0 0 – 17 – frac 1110 1111 000 closest to 1 below closest to 1 above largest norm CS 213, F’ 06

Distribution of Values 6 -bit IEEE-like format n e = 3 exponent bits n f = 2 fraction bits Bias is 3 n Notice how the distribution gets denser toward zero. – 18 – CS 213, F’ 06

Distribution of Values (close-up view) 6 -bit IEEE-like format n e = 3 exponent bits n f = 2 fraction bits Bias is 3 n Note: Smooth transition between normalized and denormalized numbers due to definition E = 1 - Bias for denormalized values – 19 – CS 213, F’ 06

Interesting Numbers Description exp Zero 00… 00 0. 0 Smallest Pos. Denorm. 00… 00 00… 01 2– {23, 52} X 2– {126, 1022} frac Numeric Value Single 1. 4 X 10– 45 n Double 4. 9 X 10– 324 n Largest Denormalized 00… 00 11… 11 (1. 0 – ) X 2– {126, 1022} Single 1. 18 X 10– 38 n Double 2. 2 X 10– 308 n Smallest Pos. Normalized 00… 01 00… 00 n 1. 0 X 2– {126, 1022} Just larger than largest denormalized One 01… 11 00… 00 1. 0 Largest Normalized 11… 10 11… 11 (2. 0 – ) X 2{127, 1023} Single 3. 4 X 1038 n Double 1. 8 X 10308 n – 20 – CS 213, F’ 06

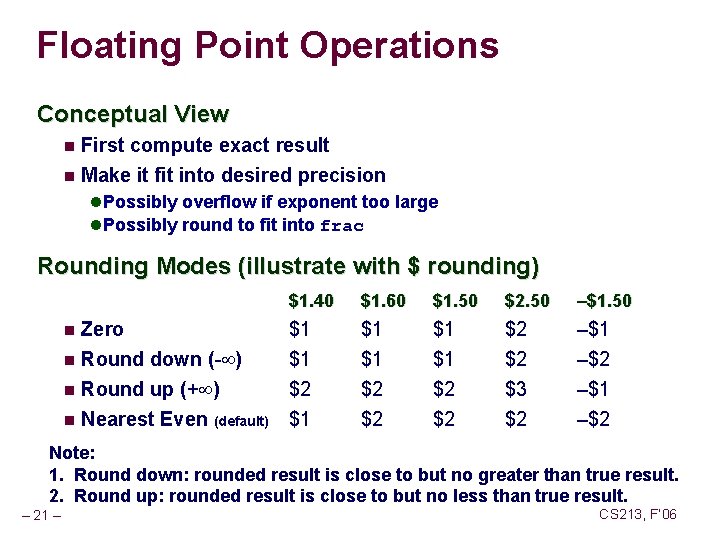
Floating Point Operations Conceptual View n First compute exact result n Make it fit into desired precision l Possibly overflow if exponent too large l Possibly round to fit into frac Rounding Modes (illustrate with $ rounding) Zero n Round down (- ) n Round up (+ ) n Nearest Even (default) n $1. 40 $1. 60 $1. 50 $2. 50 –$1. 50 $1 $1 $2 $1 $1 $1 $2 $2 $3 $2 –$1 –$2 Note: 1. Round down: rounded result is close to but no greater than true result. 2. Round up: rounded result is close to but no less than true result. – 21 – CS 213, F’ 06

Closer Look at Round-To-Even Default Rounding Mode n All others are statistically biased l Sum of set of positive numbers will consistently be over- or under- estimated Applying to Other Decimal Places / Bit Positions n When exactly halfway between two possible values l Round so that least significant digit is even n E. g. , round to nearest hundredth 1. 2349999 1. 2350001 1. 2350000 1. 2450000 – 22 – 1. 23 1. 24 (Less than half way) (Greater than half way) (Half way—round up) (Half way—round down) CS 213, F’ 06

Rounding Binary Numbers Binary Fractional Numbers “Even” when least significant bit is 0 n Half way when bits to right of rounding position = 100… 2 n Examples Round to nearest 1/4 (2 bits right of binary point) Value Binary Rounded Action Rounded Value 2 3/32 10. 000112 10. 002 (<1/2—down) 2 2 3/16 10. 001102 10. 012 (>1/2—up) 2 1/4 2 7/8 10. 111002 11. 002 (1/2—up) 3 2 5/8 10. 101002 10. 102 (1/2—down) 2 1/2 n – 23 – CS 213, F’ 06

FP Multiplication Operands (– 1)s 1 M 1 2 E 1 * (– 1)s 2 M 2 2 E 2 Exact Result (– 1)s M 2 E n n n Sign s: s 1 ^ s 2 Significand M: M 1 * M 2 Exponent E: E 1 + E 2 Fixing n If M ≥ 2, shift M right, increment E n If E out of range, overflow Round M to fit frac precision n Implementation n – 24 – Biggest chore is multiplying significands CS 213, F’ 06

FP Addition Operands (– 1)s 1 M 1 2 E 1 (– 1)s 2 M 2 2 E 2 n E 1–E 2 (– 1)s 1 M 1 Assume E 1 > E 2 Exact Result (– 1)s M 2 E n (– 1)s 2 M 2 + Sign s, significand M: l Result of signed align & add n Exponent E: E 1 Fixing n If M ≥ 2, shift M right, increment E n if M < 1, shift M left k positions, decrement E by k Overflow if E out of range Round M to fit frac precision n – 25 – n CS 213, F’ 06

Mathematical Properties of FP Add Compare to those of Abelian Group n Closed under addition? l YES. But may generate infinity or Na. N n Commutative? l YES n Associative? l No. Overflow and inexactness of rounding » (3. 14+1 e 10)-1 e 10=0 (rounding) » 3. 14+(1 e 10 -1 e 10)=3. 14 n 0 is additive identity? l YES n Every element has additive inverse l ALMOST Except for infinities & Na. Ns Monotonicity a ≥ b a+c ≥ b+c? l ALMOST Except for Na. Ns – 26 – CS 213, F’ 06

Math. Properties of FP Mult Compare to Commutative Ring n Closed under multiplication? l. YES. But may generate infinity or Na. N n Multiplication Commutative? l. YES n Multiplication is Associative? l. NO. Possibility of overflow, inexactness of rounding l (1 e 20*1 e 20)*1 e-20 = infinity, but 1 e 20*(1 e 20*1 e-20) = 0 n 1 is multiplicative identity? l. YES n Multiplication distributes over addition? l. NO. Possibility of overflow, inexactness of rounding l 1 e 20*(1 e 20 -1 e 20) = 0, but 1 e 20*1 e 20 – 1 e 20*1 e 20 = Na. N Monotonicity a ≥ b & c ≥ 0 a *c ≥ b *c? – 27 – l. ALMOST Except for Na. Ns CS 213, F’ 06

Floating Point in C C Guarantees Two Levels float double single precision double precision Conversions n n Casting between int, float, and double changes numeric values Double or float to int l Truncates fractional part l Like rounding toward zero l Not defined when out of range » Generally saturates to TMin or TMax n int to double l Exact conversion, as long as int has ≤ 53 bit word size n int to float l Will be rounded – 28 – CS 213, F’ 06

Answers to Floating Point Puzzles int x = …; float f = …; Assume neither d nor f is NAN double d = …; • x == (int)(float) x No: 24 bit significand • x == (int)(double) x Yes: 53 bit significand • f == (float)(double) f Yes: increases precision • d == (float) d No: loses precision • f == -(-f); Yes: Just change sign bit • 2/3 == 2/3. 0 No: 2/3 == 0 • d < 0. 0 ((d*2) < 0. 0) Yes! • d > f -f > -d Yes! (symmetric value range) • d * d >= 0. 0 Yes! • (d+f)-d == f No: Not associative – 29 – CS 213, F’ 06

Ariane 5 n Exploded 37 seconds after liftoff n Cargo worth $500 million Why n n Computed horizontal velocity as floating point number Converted to 16 -bit integer Worked OK for Ariane 4 Overflowed for Ariane 5 l Used same software – 30 – CS 213, F’ 06

Summary IEEE Floating Point Has Clear Mathematical Properties n n Represents numbers of form M X 2 E Not the same as real arithmetic l Violates associativity/distributivity l Makes life difficult for compilers & serious numerical applications programmers – 31 – CS 213, F’ 06