CS 212 LECTURE 04 PROGRAMMING LANGUAGES PARSE TREE

PARSE TREE • The grammar is a set of rules that say how to

PARSE TREE <sentence> <noun-phrase><verb-phrase> <noun-phrase> <article><adjective><noun> <noun-phrase> <article><noun> <verb-phrase> <verb><adverb> | <verb> <article> a

PARSE TREE • Example, the sentence is “the large rabbit hops quickly” Derivation :

PARSE TREE • We can draw a tree from the derivation which is call

PARSE TREE • Parse tree : On the left child node, we add <article>,

PARSE TREE • Continue adding child node from the leftmost derivation to the parse

PARSE TREE • Now, let try the right most derivation : <sentence> <noun-phrase><verb-phrase> à<noun-phrase><verb><adverb>

PARSE TREE • Parse tree : we start with <sentence> is a root and

• Continue adding child node from the rightmost derivation to the parse tree.

• Some Pascal production rules <expression> <simple expression> <term> | <sign><term> | <simple

<unsigned constant> <unsigned number> <unsigned integer> | <unsigned real> <unsigned integer> <digit><unsigned integer> |

Example : Uses Pascal production rules to find the leftmost derivation that given the

AMBIGUOUS • A context free grammar G is ambiguous if there is a string

EXAMPLE Let G be the grammar S a. S | Sb | ab |

• Draw a parse tree, Parse tree 1: Parse tree 2 : we

EXAMPLE Let G be the grammar S → AB | C A → a.

Two leftmost parse tree of string aabbccdd : 22

TRY THIS • CFG G have production rules : S AS | A A

Slides: 23

Download presentation

CS 212 LECTURE 04 PROGRAMMING LANGUAGES

PARSE TREE • The grammar is a set of rules that say how to build a tree— a parse tree • You put <S> at the root of the tree • The grammar’s rules say how children can be added at any point in the tree • For instance, the rule <S> : : = <NP> <V> <NP> • says you can add nodes <NP>, <V>, and <NP>, in that order, as children of <S>

PARSE TREE • Example, the sentence is “the large rabbit hops quickly” Derivation : <sentence> <noun-phrase><verb-phrase> à<article><adjective><noun><verb-phrase> àthe large<noun><verb-phrase> àthe large rabbit <verb><adverb> àthe large rabbit hops quickly

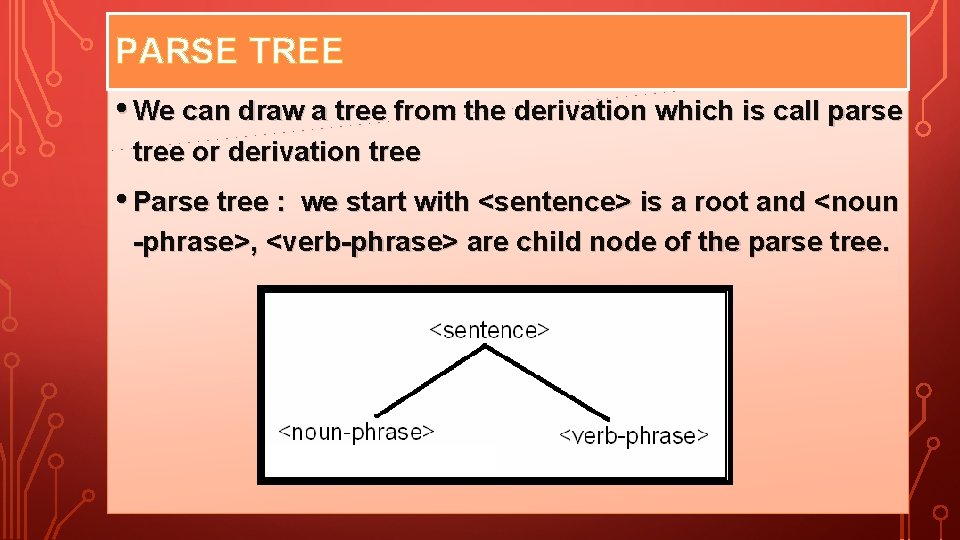
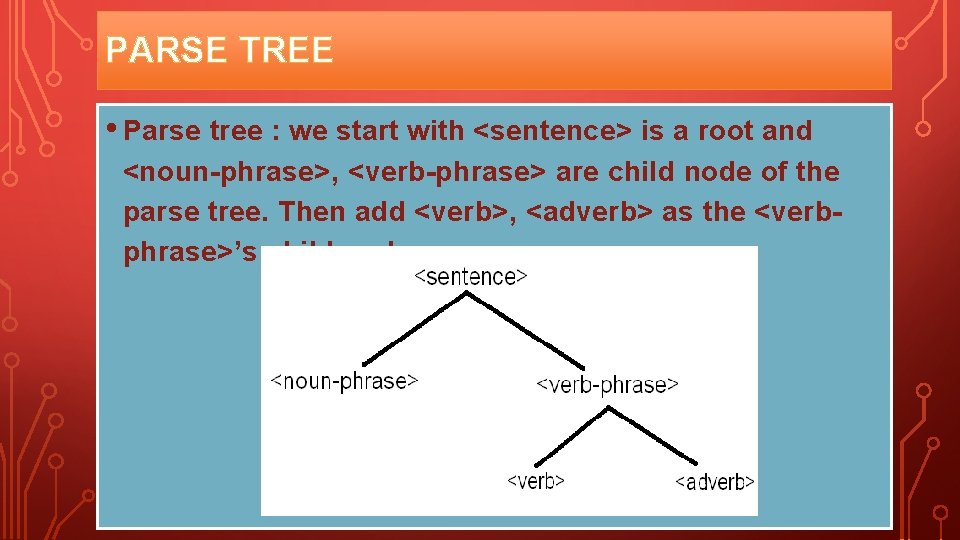
PARSE TREE • We can draw a tree from the derivation which is call parse tree or derivation tree • Parse tree : we start with <sentence> is a root and <noun -phrase>, <verb-phrase> are child node of the parse tree.

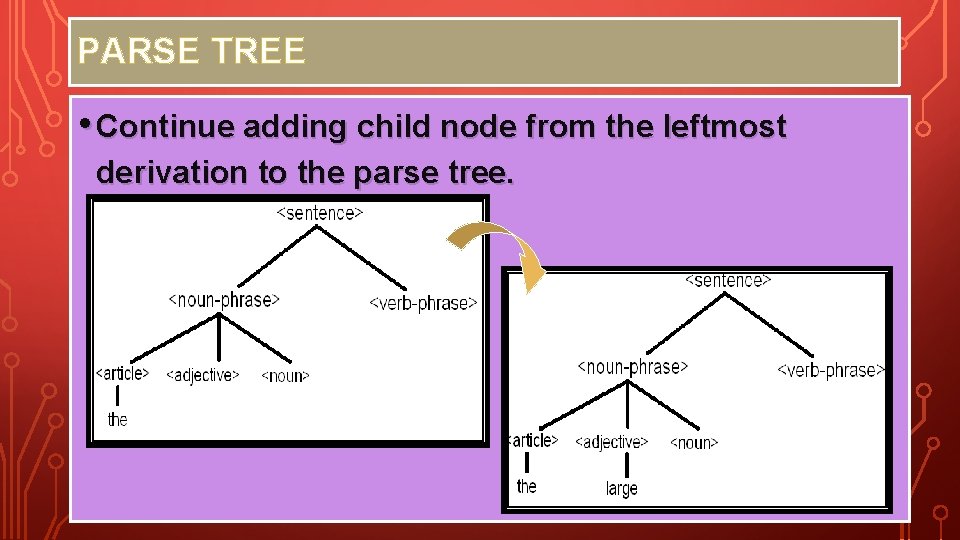
PARSE TREE • Parse tree : On the left child node, we add <article>, <adjective>, <noun> to be <noun-pharse> ’s child node.

PARSE TREE • Continue adding child node from the leftmost derivation to the parse tree.

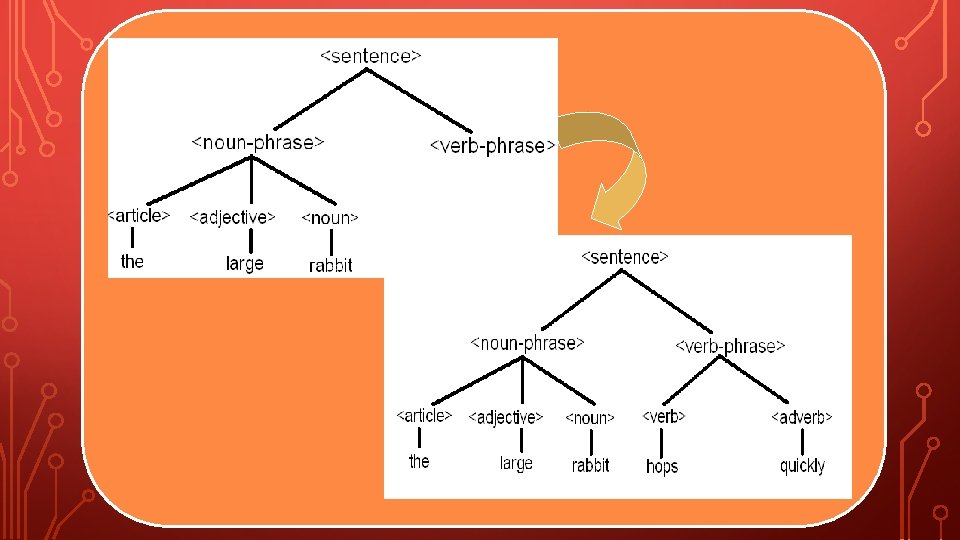
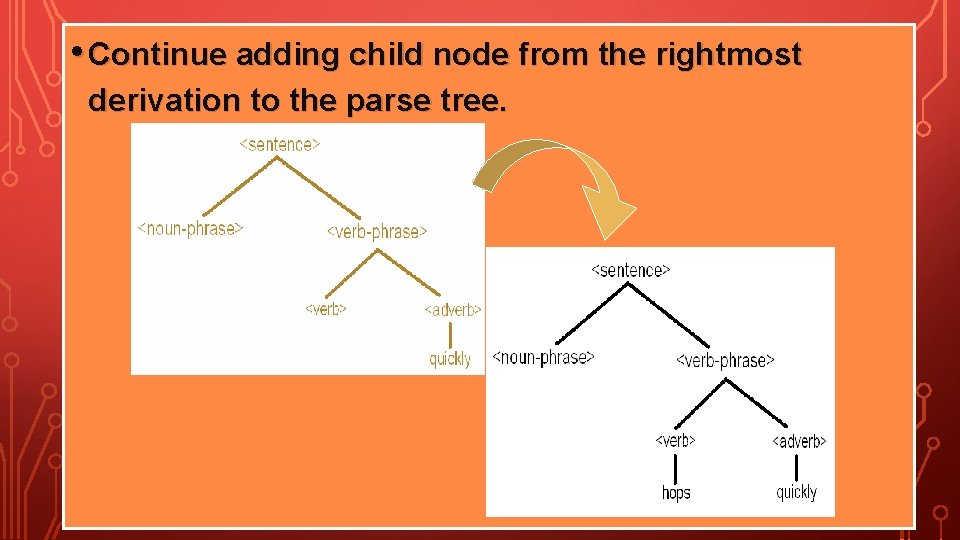
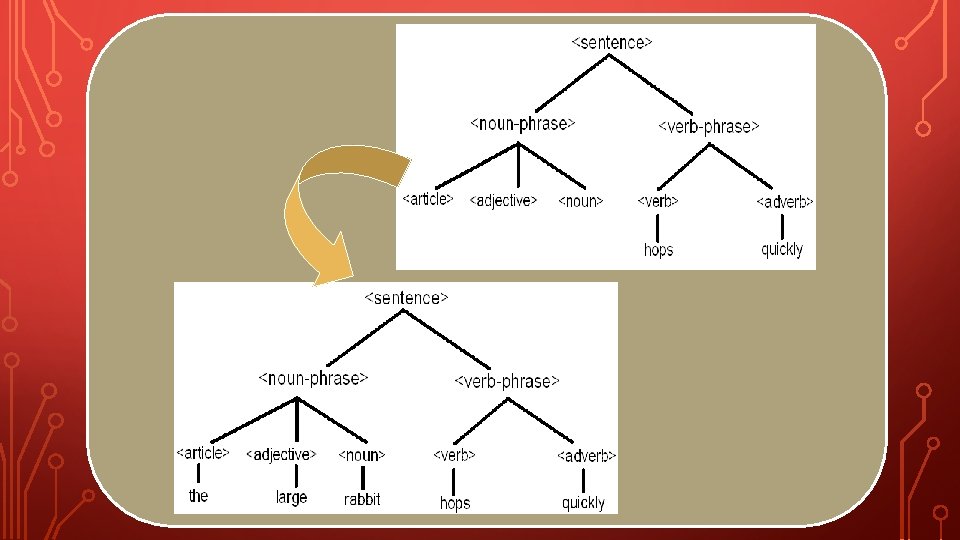
PARSE TREE • Now, let try the right most derivation : <sentence> <noun-phrase><verb-phrase> à<noun-phrase><verb><adverb> à<noun-phrase><verb>quickly à<noun-phrase> hops quickly à<article><adjective><noun> hops quickly à<article><adjective> rabbit hops quickly à<article> large rabbit hops quickly àthe large rabbit hops quickly

PARSE TREE • Parse tree : we start with <sentence> is a root and <noun-phrase>, <verb-phrase> are child node of the parse tree. Then add <verb>, <adverb> as the <verbphrase>’s child node.

• Continue adding child node from the rightmost derivation to the parse tree.

<unsigned constant> <unsigned number> <unsigned integer> | <unsigned real> <unsigned integer> <digit><unsigned integer> | <digit > <identifier> <letter><identifier tail> | <digit><identifier tail> | <sign> + | <digit> 0 | 1 | 2 |…| 9 <letter> a | b | c | … | z

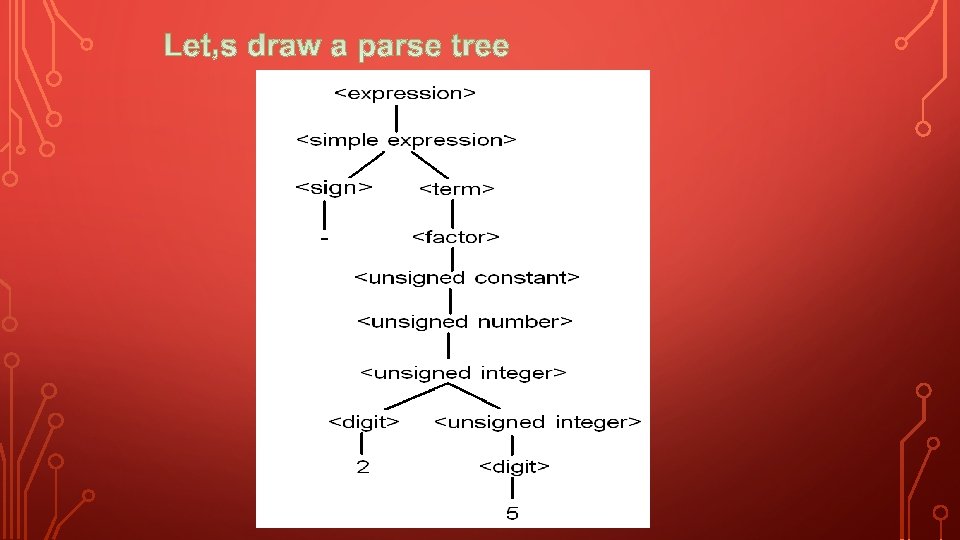
Example : Uses Pascal production rules to find the leftmost derivation that given the number - 25. Derivation is <expression> <simple expression> <sign><term> - <factor> - <unsigned constant> - <unsigned number> - <unsigned integer> - <digit><unsigned integer> - 2<digit> - 25

AMBIGUOUS • A context free grammar G is ambiguous if there is a string w L(G) that can be derived by two distinct leftmost derivations. A grammar that is not ambiguous is called unambiguous. • Example : S a. S | Sa | a we need to generate string aa S aa (1) S Sa aa (2) String aa can have two leftmost derivation. This is an ambiguous. 17

AMBIGUOUS • A context free grammar G is ambiguous if there is a string w L(G) that can be derived by two distinct derivation tree • From the last example we can draw the parse tree from (1) and (2) : 18

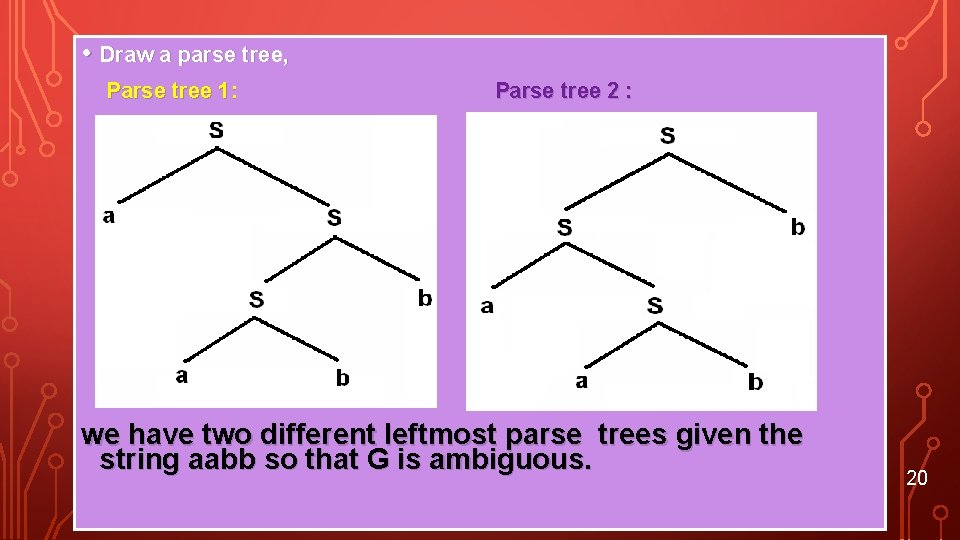
EXAMPLE Let G be the grammar S a. S | Sb | ab | SS Construct two leftmost derivations of the string aabb. Show that G is ambiguous. Two leftmost derivations are 1. S a. Sb aabb 2. S Sb aabb 19

• Draw a parse tree, Parse tree 1: Parse tree 2 : we have two different leftmost parse trees given the string aabb so that G is ambiguous. 20

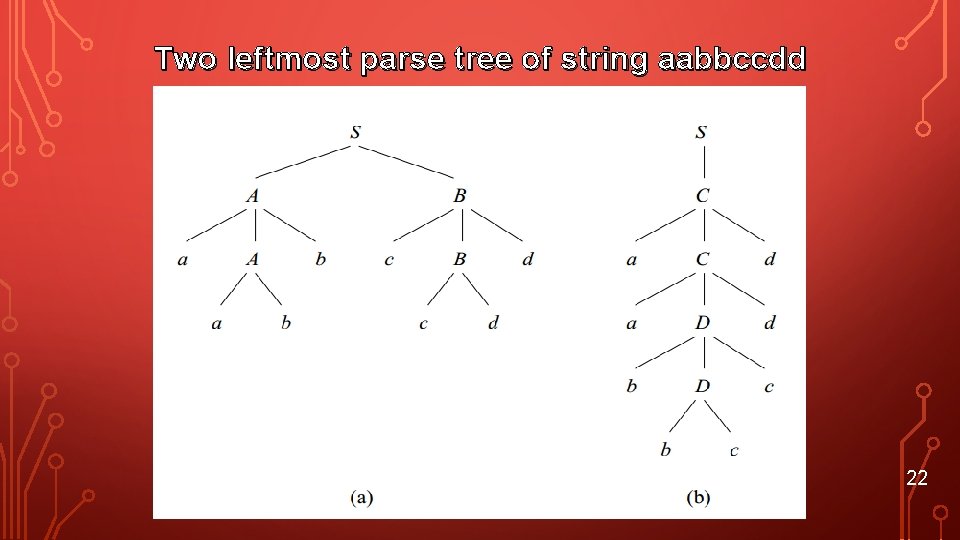
EXAMPLE Let G be the grammar S → AB | C A → a. Ab | ab B → c. Bd | cd C → a. Cd | a. Dd D → b. Dc | bc Construct two leftmost derivations of the string aabbccdd. Show that G is ambiguous. Two leftmost derivations are : 1. S AB a. Ab. B aabb. B aabbc. Bd aabbccdd 2. S C a. Cd aa. Ddd aab. Dcdd aabbccdd 21

Two leftmost parse tree of string aabbccdd : 22

TRY THIS • CFG G have production rules : S AS | A A 1 | 01 find two distinct leftmost derivation and parse tree to generate string 00111 • CFG G have production rules : S S+S | S-S | S*S | S/S | a find two distinct leftmost derivation and parse tree to generate string a+a+a • CFG G have production rules : S Sb. S | Sc. S | Sd. S |a | e find two distinct leftmost derivation and parse tree to generate string abedecaba 23