CS 212 Data Structures and Algorithms Lecture 7

CS 212: Data Structures and Algorithms Lecture # 7 Recursion

Outline Towards Recursion Recursive Programming Rules of Recursion Exercises 2

Towards Recursion Factorial Function Given a +ive integer n, n factorial is defined as the product of all integers between 1 and n, including n. n != 1 if n == 0 n != n*(n-1) * (n-2) * - - -* 1 if n > 0 Algorithm that accepts an integer n and returns the value of n! prod = 1; for(x = n; x > 0; x--) prod*= x; return(prod); This algorithm is an iterative algorithm 3

Towards Recursion Multiplying n by the product of all integers from n-1 to 1 yields the product of all integers from n to 1. For any n > 0, we see that n! equals n * (n-1)! n! = 1 if n == 0 n! = n(n-1)! if n > 0 Is this a recursive definition? A definition which defines an object in terms of a simpler case of itself, is called a recursive definition 4

Towards Recursion Multiplication of Natural Number The product a * b, where a and b are positive integers, may be defined as a*b=a if b ==1 a * b = a * (b-1) + a if b > 1 e. g. 6*3=6*2+6 =6*1+6+6 =6+6+6 = 18 6

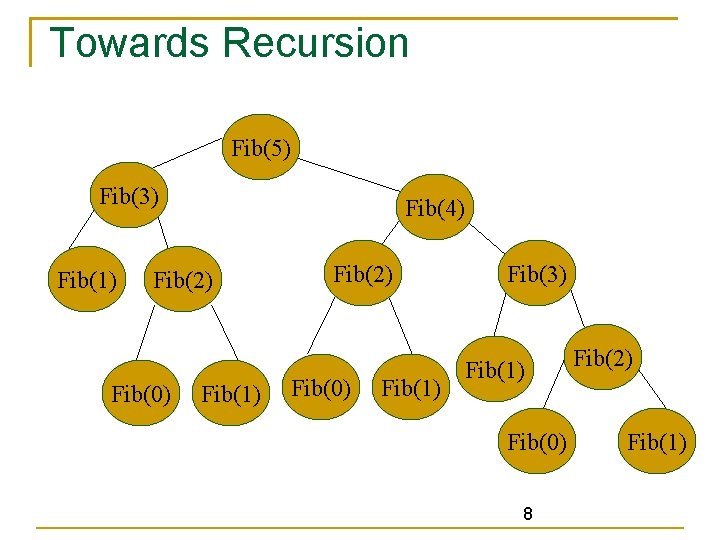
Towards Recursion Fibonnacci Sequence 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, . . . . Each element is the sum of the two preceding elements with fib(0) = 0 fib(1) = 1 fib(n) = n if n ==0 or n ==1 fib(n) = fib(n-2) + fib(n-1) if n >= 2 e. g. Compute fib(5) 7

Towards Recursion Fib(5) Fib(3) Fib(1) Fib(4) Fib(2) Fib(0) Fib(1) Fib(3) Fib(1) Fib(0) 8 Fib(2) Fib(1)

Towards Recursion All these problems have a recursive definition A definition which defines an object in terms of a simpler case of itself, is called a recursive definition 9

Recursion Every recursive definition has two parts, A Recursive part & A Non-Recursive part, also called as Base Case e. g. in the recursive definition of n! = 1 if n == 0 Base Case n! = n*(n-1) * (n-2) *…* 1 if n > 0 Recursive Part 10

Recursion The recursive part of the n! definition is used several times, terminating with the non-recursive part 1. 5! = 5 * 4! 2. - - - - 4! = 4 * 3! 3. - - - - 3! = 3 * 2! 4. - - - - - - 2! = 2 * 1! 5. - - - - - - - - 1! = 1 * 0! 6. - - - - - - - - -0! = 1 Solve from line 6 to 1. 6´- - - - - 0! = 1 5´- - - - - 1! = 1*0! = 1 * 1 = 1 4´- - - - - 2! = 2*1! = 2 * 1 = 2 3´- - - - - 3! = 3*2! = 3 * 2 = 6 2´- - - - - 4! = 4*3! = 4 * 6 = 24 1´- - - - - 5! = 5*4! = 5 *24 = 120 11

Recursion All recursive definitions have to have a base case If they didn't, there would be no way to terminate the recursive path Such a definition would cause infinite recursion This problem is similar to an infinite loop 12

Recursion How can we translate recursive definition into a computer program? Recursion is a fundamental programming technique that can provide a solution to the problems that have a recursive definition 13

Recursive Programming A method/function which can invoke itself, if set up that way, is called a recursive method/function The code of a recursive method/function must be structured to handle both the base case and the recursive case 14

Recursive Programming Each call to the method sets up a new execution environment, with new parameters and local variables As always, when the method completes, control returns to the method that invoked it (which may be an earlier invocation of itself) 15

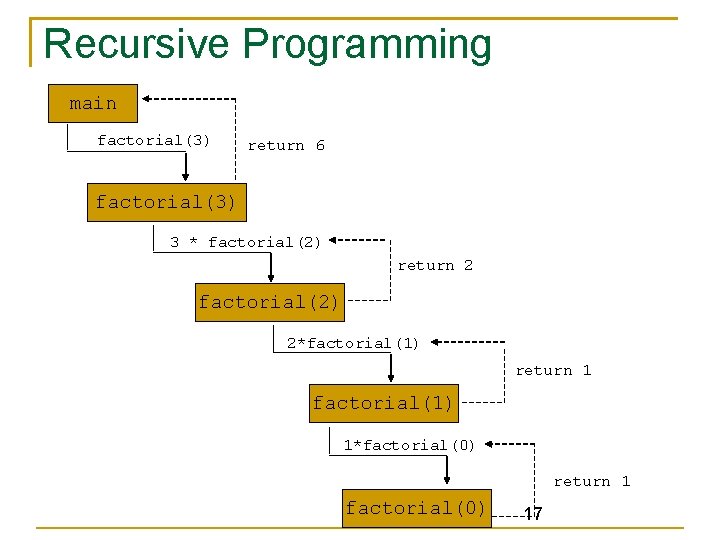
Recursive Programming Consider again the recursive definition of the factorial of a positive integer. n! = 1 if n == 0 Base Case n! = n*(n-1) * (n-2) * …* 1 if n > 0 Recursive Part We can write the recursive function using this definition as int factorial(int n) { if(n == 0) //Base Case return 1; else return n * factorial(n-1); //Recursion } 16

Recursive Programming main factorial(3) return 6 factorial(3) 3 * factorial(2) return 2 factorial(2) 2*factorial(1) return 1 factorial(1) 1*factorial(0) return 1 factorial(0) 17

Recursive Programming Multiplication of natural numbers: The product a * b, where a and b are positive integers, may be defined as a*b=a if b ==1 a * b = a * (b-1) + a if b > 1 int multiplication(int a, int b) { if(b == 1) return a; else if(b > 1) return multiplication(a, b-1) + a; } 18

Recursive Programming Fibonnacci Sequence fib(n) = n if n ==0 or n ==1 fib(n) = fib(n-2) + fib(n-1) if n >= 2 int fib(int n) { if(n == 0 || n == 1) return n; else return fib(n-2) + fib(n-1); } 19

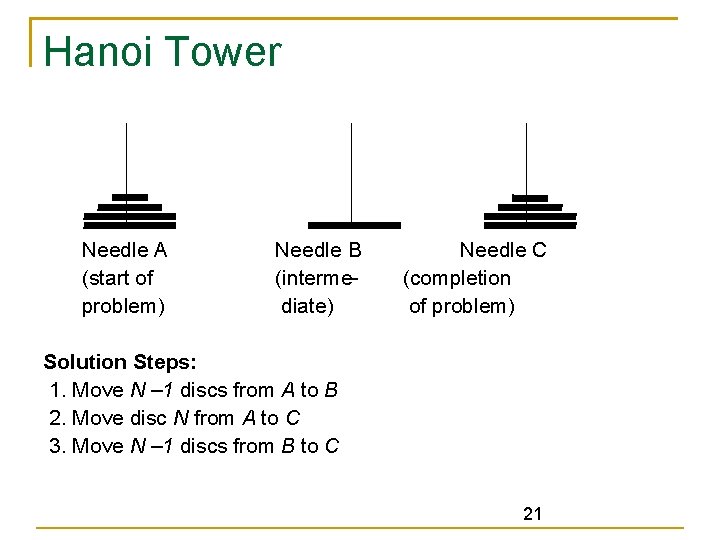
Hanoi Tower Problem Statement Given N discs (of strictly decreasing size) stacked on one needle and two empty needles, it is required to stack all the discs onto a second needle in decreasing order of size The third needle may be used as temporary storage The movement of the discs is restricted by the following rules: 1. Only one disc may be moved at a time 2. A disc may be moved from any needle to any other 3. At no time may a larger disc rest upon a smaller disc 20

Hanoi Tower Needle A (start of problem) Needle B (intermediate) Needle C (completion of problem) Solution Steps: 1. Move N – 1 discs from A to B 2. Move disc N from A to C 3. Move N – 1 discs from B to C 21

Hanoi Tower void tower(char source, char destination, char intermediate, int n) { if(n==1) { cout<<"Move disk 1 from needle "<<source<<" to needle "<<destination<<endl; } else { tower(source, intermediate, destination, n-1); cout<<"Move disk "<<n<<" from needle "<<source<<" to needle "<<destination<<endl; tower(intermediate, destination, source, n-1); } } 22

Hanoi Tower tower(‘A’, ‘C’, ‘B’, 3); //A is source, C is destination //B is intermediate Move disk 1 from A to C Move disk 2 from A to B Move disk 1 from C to B Move disk 3 from A to C Move disk 1 from B to A Move disk 2 from B to C Move disk 1 from A to C 23

Rules of Recursion Base Case There must be a way out for a recursive algorithm It must not generate an infinite sequence of calls on itself Without a non-recursive exit, no recursive function can ever be computed Making Progress For the cases that are to be solved recursively, the recursive call must always be to a case that makes progress toward a base case 24

Rules of Recursion Example 1 - - - int Bad(int N) 2 - - - { 3 - - - - -if(N == 0) 4 - - - -- - - return 0; 5 - - - -- --else 6 - - - return Bad (N / 3+1) + N - 1; 7 - - - } 25

Rules of Recursion Design Rule Assume that all the recursive calls work Never duplicate work by solving the same instance of a problem in separate recursive calls Example: Fibonacci Numbers 26

Exercises Example A +ive integer to be printed Assume that only I/O routines available will take a single digit number and output it to the terminal Write a recursive algorithm to print the number digit by digit void print_out(int N) { if(N < 10) cout<<N; else { print_out(N/10); cout<<(N%10); } } 27

Exercises 1. The problem of computing the sum of all the numbers between 1 and any positive integer N can be recursively defined as: N N-1 = N i=1 = + N-2 = N + (N-1) + i=1 etc. 28

Exercises int sum(int n) { if(n==1) return n; else return n + sum(n-1); } 29

Exercises 1. Ackerman's function is defined recursively on a non negative integers as follows A(m, n) = n + 1 if m = = 0 A(m, n) = A(m-1, 1) if m != 0, n = = 0 A(m, n) = A(m-1, A(m, n-1)) if m != 0, n != 0 30

Exercises int ackerman(int m, int n) { if(m==0) return n+1; if(m!=0&&n==0) return ackerman(m-1, 1); if(m!=0&&n!=0) return ackerman(m-1, ackerman(m, n-1)); } 31

Exercises 1. The Greatest Common Divisor (GCD) of two positive integers x and y is defined as GCD(x, y) = y if (y <= x && x % y ==0) GCD(x, y) = GCD(y, x) if (x < y) GCD(x, y) = GCD(y, x % y) otherwise 32

Exercises int GCD(int x, int y) { if (y <= x && x % y ==0) return y; else if (x < y) return GCD(y, x); else return GCD(y, x % y); } 33