CS 2100 Computer Organisation http www comp nus

CS 2100 Computer Organisation http: //www. comp. nus. edu. sg/~cs 2100/ Logic Gates and Circuits (AY 2008/9) Semester 2

WHERE ARE WE NOW? n n n Number systems and codes Preparation: 2 weeks Boolean algebra Logic gates and circuits Simplification Logic Design: 3 weeks Combinational circuits Sequential circuits Performance Assembly language Computer The processor: Datapath and control organisation Pipelining Memory hierarchy: Cache Input/output CS 2100 Logic Gates and Circuits 2

LOGIC GATES AND CIRCUITS n n n n Gate Symbols Inverter/AND/OR/NAND/NOR/XNOR Drawing and Analysing Logic Circuits Universal Gates SOP and NAND Circuits POS and NOR Circuits Programmable Logic Array CS 2100 Logic Gates and Circuits 3

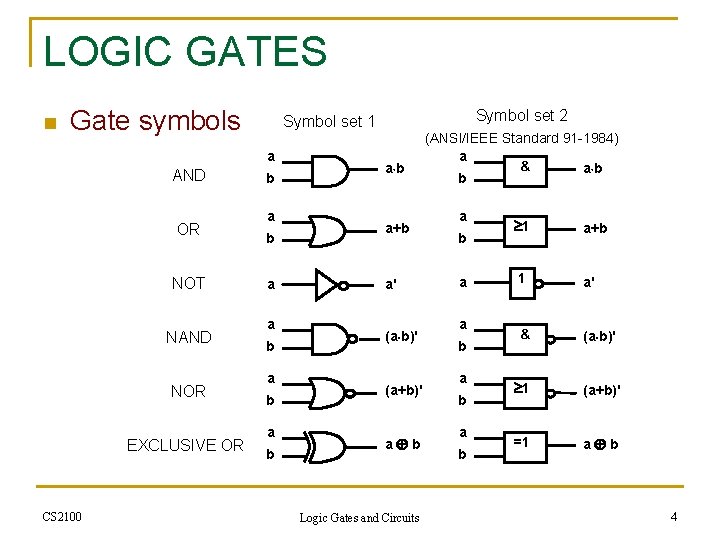
LOGIC GATES n Gate symbols a AND OR NOT NAND NOR EXCLUSIVE OR CS 2100 Symbol set 2 Symbol set 1 b a a b a b a+b a' (a b)' (a+b)' a b Logic Gates and Circuits (ANSI/IEEE Standard 91 -1984) a & a b b a a b a b 1 a+b 1 a' & (a b)' 1 (a+b)' =1 a b 4

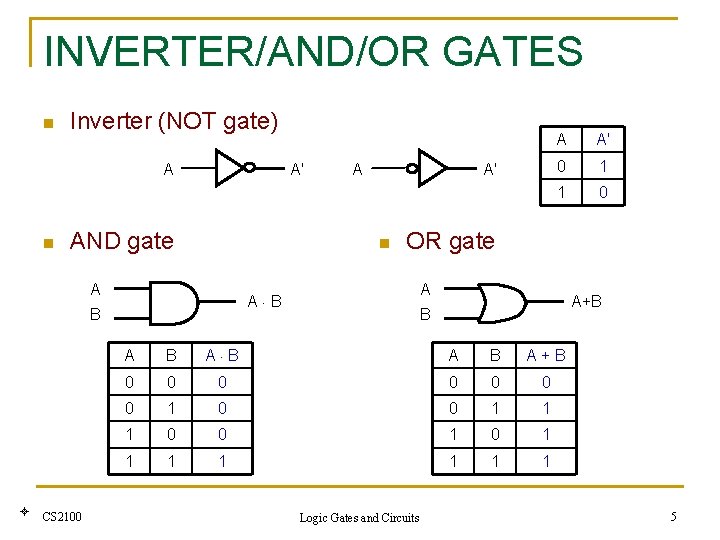
INVERTER/AND/OR GATES n Inverter (NOT gate) A n A' AND gate A' 0 1 1 0 OR gate A A B B CS 2100 A' n A A+B B A B A+B 0 0 0 0 1 1 1 0 0 1 1 1 1 Logic Gates and Circuits 5

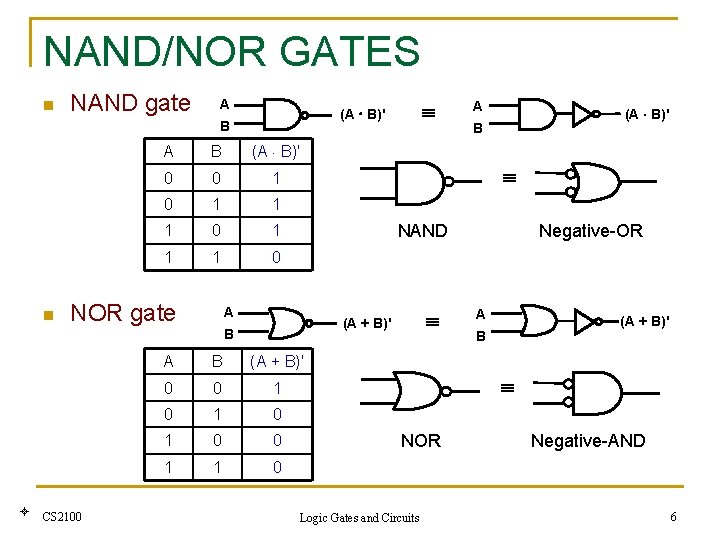
NAND/NOR GATES n NAND gate A B n A B (A B)' 0 0 1 1 1 0 NOR gate CS 2100 A (A B)' B NAND A (A + B)' B (A B)' A B (A + B)' 0 0 1 0 1 0 0 1 1 0 Negative-OR A (A + B)' B NOR Logic Gates and Circuits Negative-AND 6

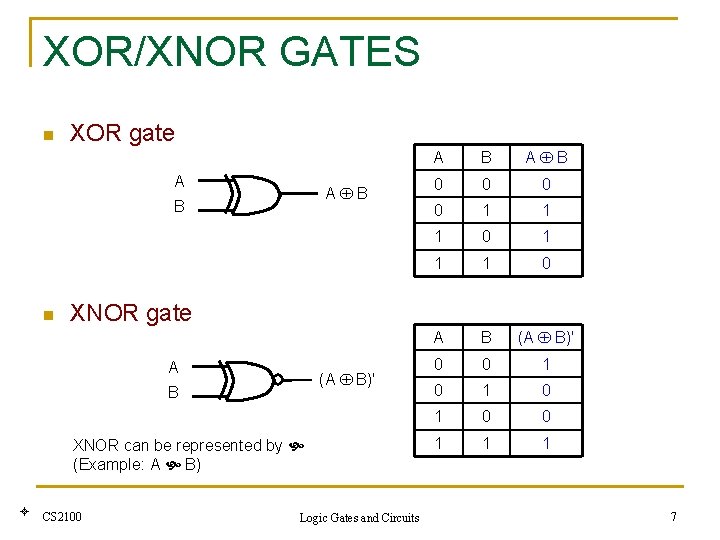
XOR/XNOR GATES n XOR gate A A B B n B A B 0 0 1 1 1 0 A B (A B)' 0 0 1 0 1 0 0 1 1 1 XNOR gate A (A B)' B XNOR can be represented by (Example: A B) A CS 2100 Logic Gates and Circuits 7

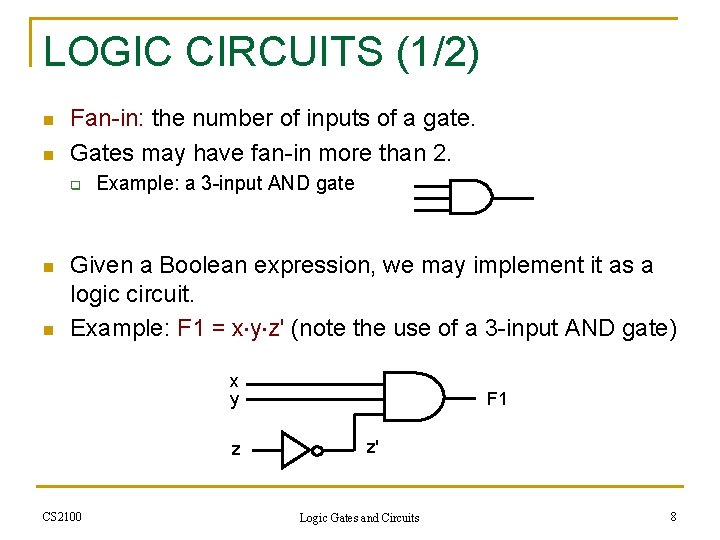
LOGIC CIRCUITS (1/2) n n Fan-in: the number of inputs of a gate. Gates may have fan-in more than 2. q n n Example: a 3 -input AND gate Given a Boolean expression, we may implement it as a logic circuit. Example: F 1 = x y z' (note the use of a 3 -input AND gate) x y z CS 2100 F 1 z' Logic Gates and Circuits 8

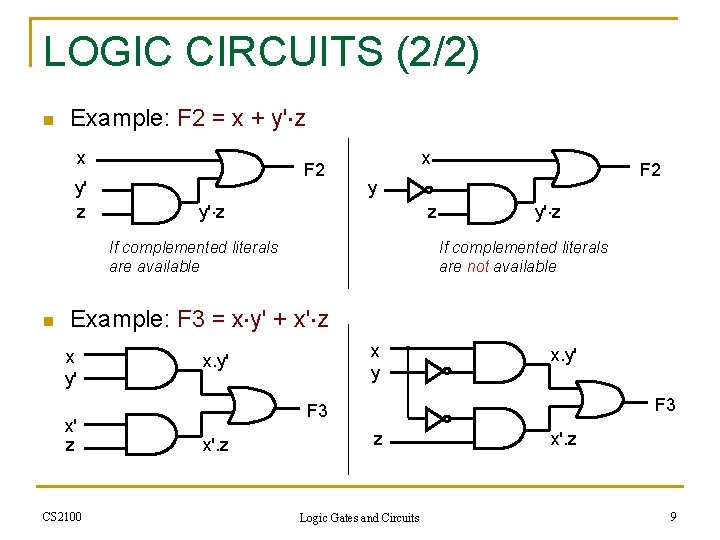
LOGIC CIRCUITS (2/2) n Example: F 2 = x + y' z x y' z F 2 x y y' z z If complemented literals are available n F 2 y' z If complemented literals are not available Example: F 3 = x y' + x' z x y' x' z CS 2100 x y x. y' F 3 x'. z z Logic Gates and Circuits x'. z 9

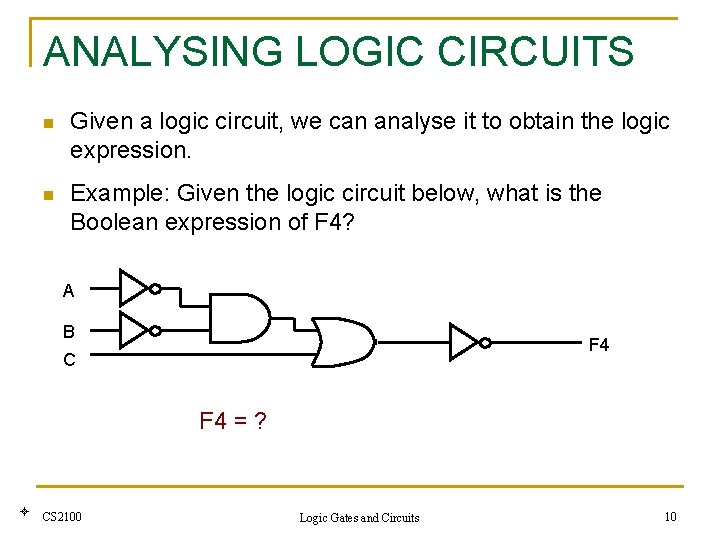
ANALYSING LOGIC CIRCUITS n Given a logic circuit, we can analyse it to obtain the logic expression. n Example: Given the logic circuit below, what is the Boolean expression of F 4? A B F 4 C F 4 = ? CS 2100 Logic Gates and Circuits 10

QUICK REVIEW QUESTIONS (1) n DLD page 77 Questions 4 -1 to 4 -4. CS 2100 Logic Gates and Circuits 11

UNIVERSAL GATES n AND/OR/NOT gates are sufficient for building any Boolean function. n We call the set {AND, OR, NOT} a complete set of logic. n However, other gates are also used: q q q CS 2100 Usefulness (eg: XOR gate for parity bit generation) Economical Self-sufficient (eg: NAND/NOR gates) Logic Gates and Circuits 12

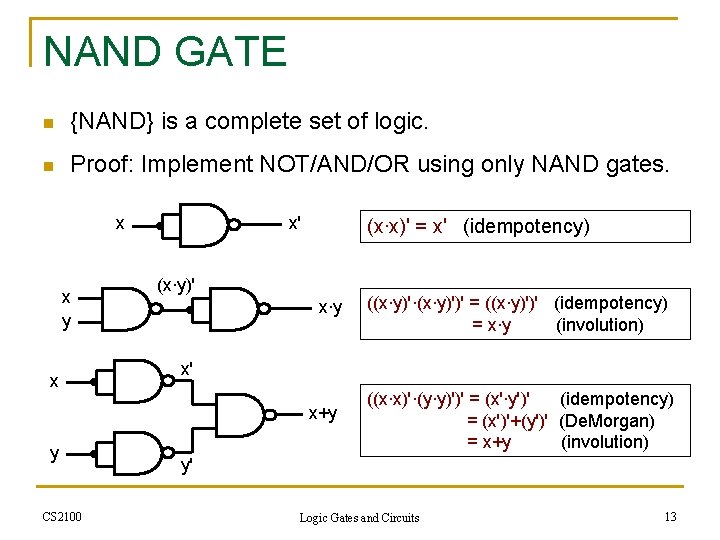
NAND GATE n {NAND} is a complete set of logic. n Proof: Implement NOT/AND/OR using only NAND gates. x x y x x' (x∙x)' = x' (idempotency) (x∙y)' x∙y x' x+y y CS 2100 ((x∙y)'∙(x∙y)')' = ((x∙y)')' (idempotency) = x∙y (involution) ((x∙x)'∙(y∙y)')' = (x'∙y')' (idempotency) = (x')'+(y')' (De. Morgan) = x+y (involution) y' Logic Gates and Circuits 13

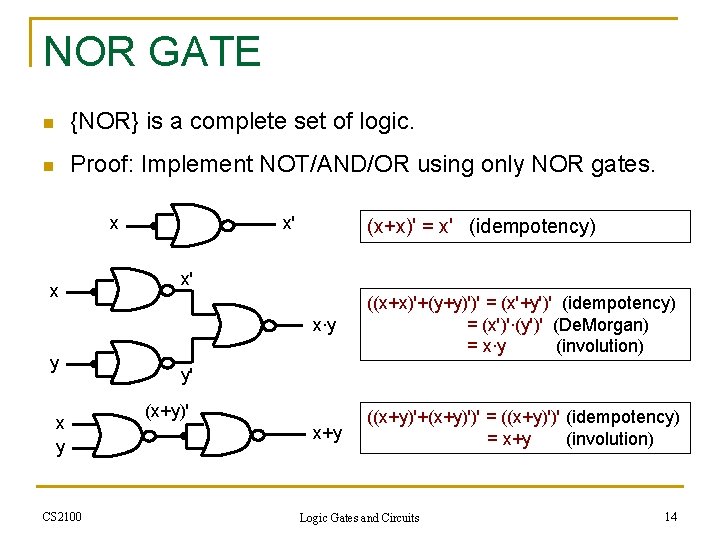
NOR GATE n {NOR} is a complete set of logic. n Proof: Implement NOT/AND/OR using only NOR gates. x x y CS 2100 x' (x+x)' = x' (idempotency) x' x∙y ((x+x)'+(y+y)')' = (x'+y')' (idempotency) = (x')'∙(y')' (De. Morgan) = x∙y (involution) x+y ((x+y)'+(x+y)')' = ((x+y)')' (idempotency) = x+y (involution) y' (x+y)' Logic Gates and Circuits 14

QUICK REVIEW QUESTIONS (2) n DLD page 77 Questions 4 -6 to 4 -8. CS 2100 Logic Gates and Circuits 15

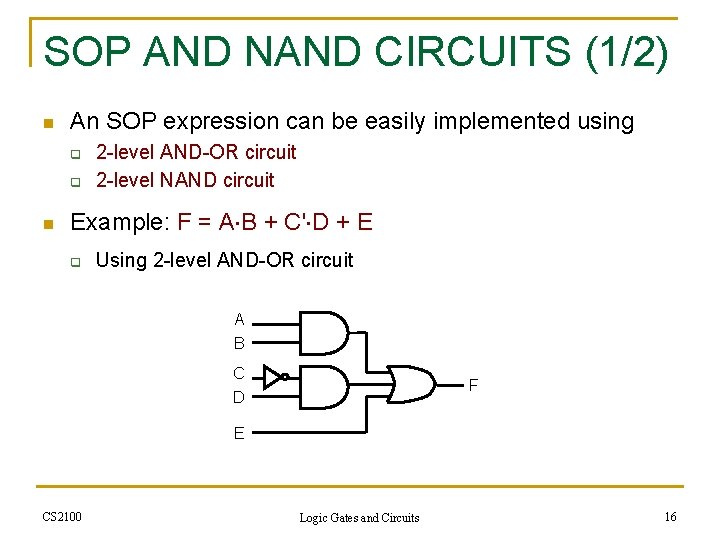
SOP AND NAND CIRCUITS (1/2) n An SOP expression can be easily implemented using q q n 2 -level AND-OR circuit 2 -level NAND circuit Example: F = A B + C' D + E q Using 2 -level AND-OR circuit A B C F D E CS 2100 Logic Gates and Circuits 16

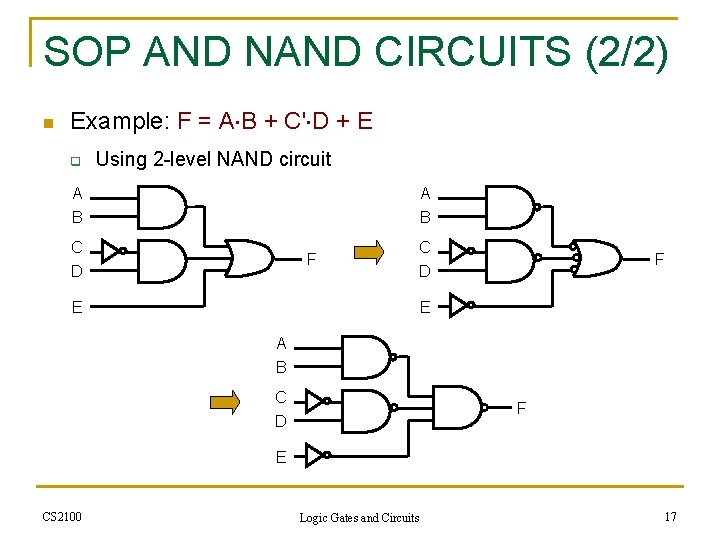
SOP AND NAND CIRCUITS (2/2) n Example: F = A B + C' D + E q Using 2 -level NAND circuit A B C F D C D E F E A B C F D E CS 2100 Logic Gates and Circuits 17

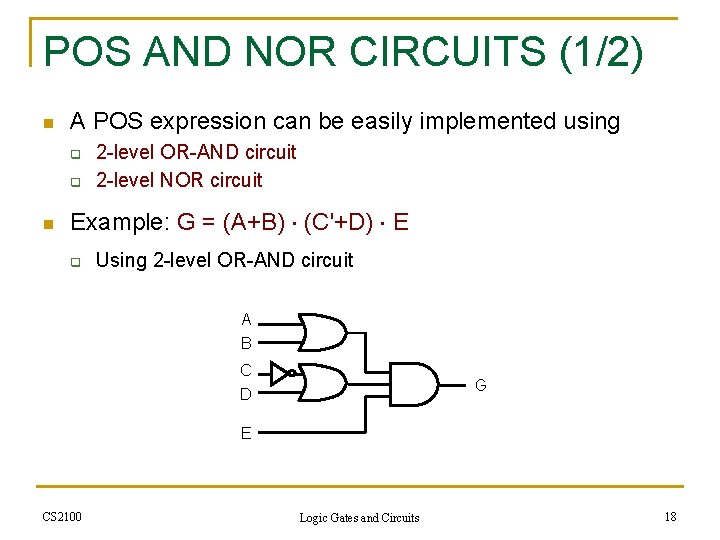
POS AND NOR CIRCUITS (1/2) n A POS expression can be easily implemented using q q n 2 -level OR-AND circuit 2 -level NOR circuit Example: G = (A+B) (C'+D) E q Using 2 -level OR-AND circuit A B C D G E CS 2100 Logic Gates and Circuits 18

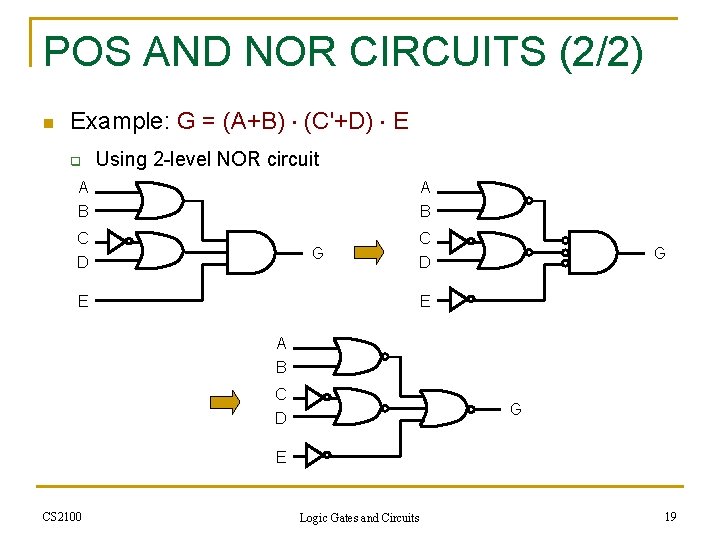
POS AND NOR CIRCUITS (2/2) n Example: G = (A+B) (C'+D) E q Using 2 -level NOR circuit A B C D G E A B C G D E CS 2100 Logic Gates and Circuits 19

READING ASSIGNMENT n Propagation Delay q n Read up DLD section 4. 5, pg 69 – 71. Integrated Circuit Logic Families q CS 2100 Read up DLD section 4. 6, pg 71 – 72. Logic Gates and Circuits 20

INTEGRATED CIRCUIT (IC) CHIP 14 13 12 4 11 5 10 6 9 7 8 CS 2100 3 GND 2 Example of a 74 LS 00 chip: Quad NAND gates. 1 n Logic Gates and Circuits Vcc = 5 v 21

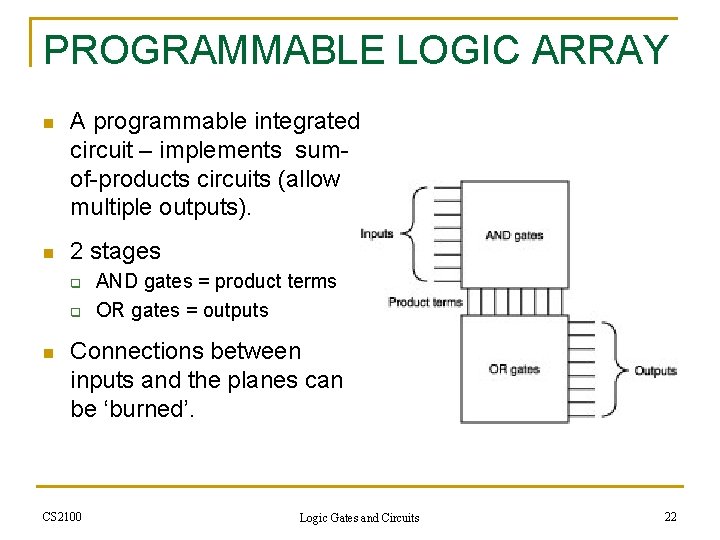
PROGRAMMABLE LOGIC ARRAY n A programmable integrated circuit – implements sumof-products circuits (allow multiple outputs). n 2 stages q q n AND gates = product terms OR gates = outputs Connections between inputs and the planes can be ‘burned’. CS 2100 Logic Gates and Circuits 22

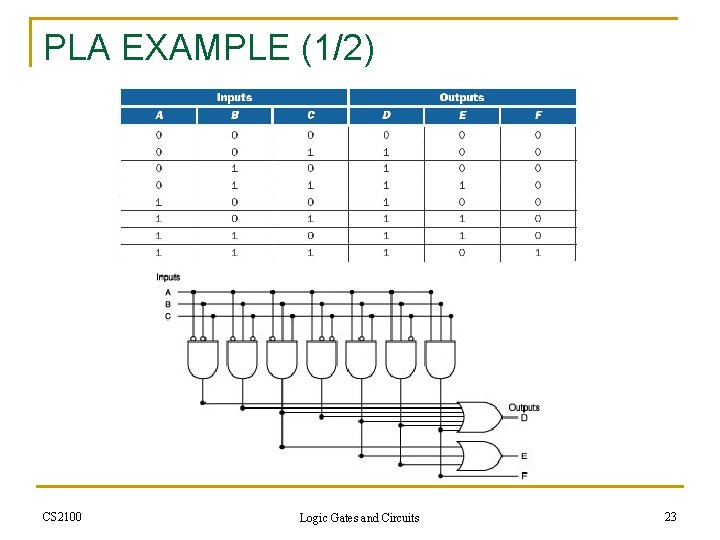
PLA EXAMPLE (1/2) CS 2100 Logic Gates and Circuits 23

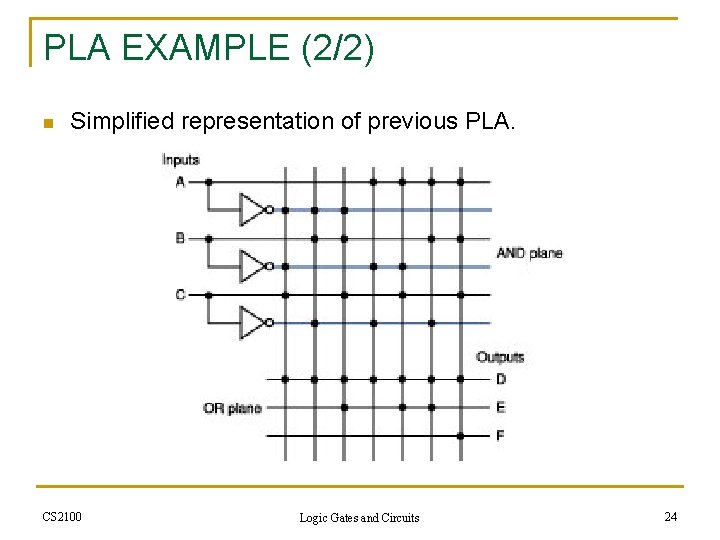
PLA EXAMPLE (2/2) n Simplified representation of previous PLA. CS 2100 Logic Gates and Circuits 24

READ ONLY MEMORY (ROM) n Similar to PLA q q q Set of inputs (called addresses) Set of outputs Programmable mapping between inputs and outputs n Fully decoded: able to implement any mapping. n In contrast, PLAs may not be able to implement a given mapping due to not having enough minterms. CS 2100 Logic Gates and Circuits 25

END CS 2100 Logic Gates and Circuits 26