CS 21 Decidability and Tractability Lecture 3 January

CS 21 Decidability and Tractability Lecture 3 January 8, 2021 CS 21 Lecture 3 1

Outline • • Nondeterministic Finite Automata Closure under regular operations • NFA, FA equivalence • • Regular Expressions FA and Regular Expressions January 8, 2021 CS 21 Lecture 3 2

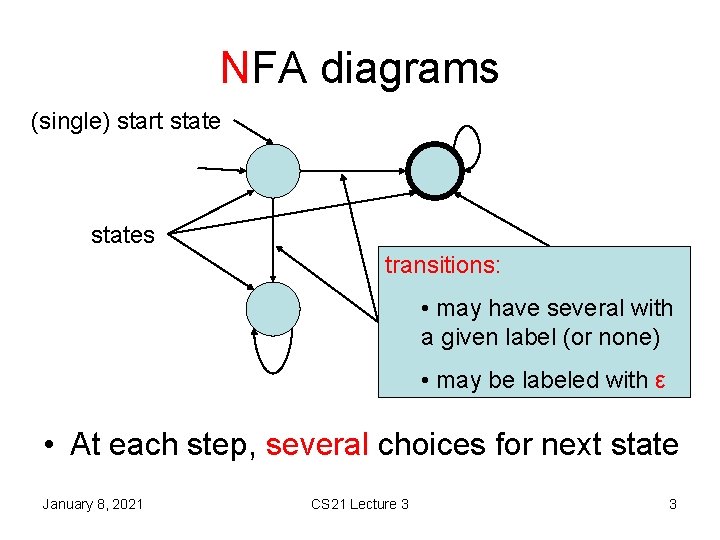
NFA diagrams (single) start states transitions: (several) accept states • may have several with a given label (or none) • may be labeled with ε • At each step, several choices for next state January 8, 2021 CS 21 Lecture 3 3

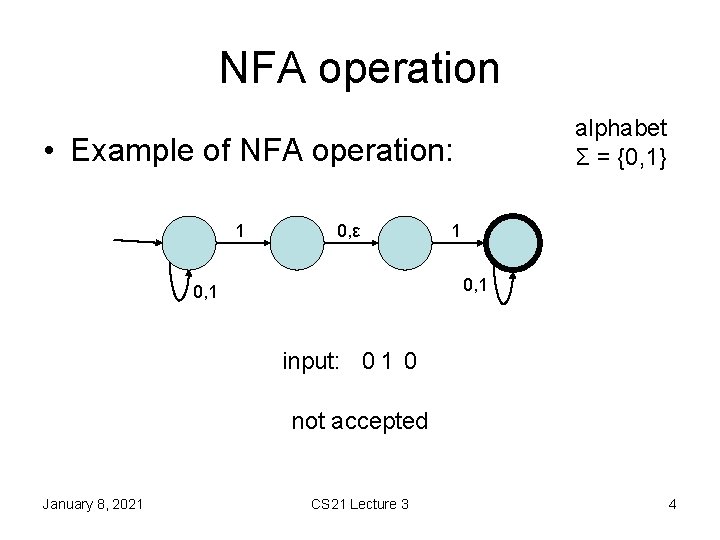
NFA operation alphabet Σ = {0, 1} • Example of NFA operation: 1 0, ε 1 0, 1 input: 0 1 0 not accepted January 8, 2021 CS 21 Lecture 3 4

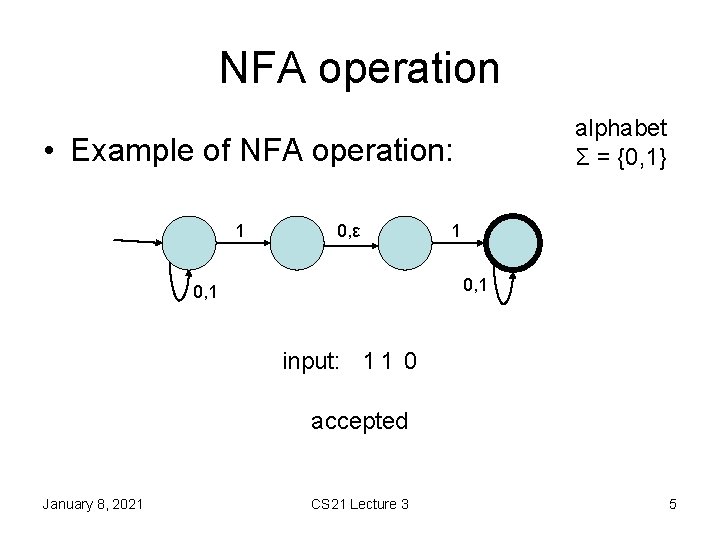
NFA operation alphabet Σ = {0, 1} • Example of NFA operation: 1 0, ε 1 0, 1 input: 1 1 0 accepted January 8, 2021 CS 21 Lecture 3 5

NFA operation • One way to think of NFA operation: • string x = x 1 x 2 x 3…xn accepted if and only if – there exists a way of inserting ε’s into x x 1εεx 2 x 3…εxn – so that there exists a path of transitions from the start state to an accept state January 8, 2021 CS 21 Lecture 3 6

NFA formal definition • January 8, 2021 “powerset of Q”: transitions the set of all labeled with alphabetsubsets of Q symbols or ε CS 21 Lecture 3 7

NFA formal definition s 1 1 0, ε s 2 s 3 1 s 4 0, 1 • Specification of this NFA in formal terms: – Q = {s 1, s 2, s 3, s 4} – Σ = {0, 1} – q 0 = s 1 – F = {s 4} January 8, 2021 δ(s 1, 0) = {s 1} δ(s 3, 0) = { } δ(s 1, 1) = {s 1, s 2} δ(s 3, 1) = {s 4} δ(s 1, ε) = { } δ(s 3, ε) = { } δ(s 2, 0) = {s 3} δ(s 4, 0) = {s 4} δ(s 2, 1) = { } δ(s 4, 1) = {s 4} δ(s 2, ε) = {s 3} δ(s 4, ε) = { } CS 21 Lecture 3 8

Formal description of NFA operation • January 8, 2021 CS 21 Lecture 3 9

Closures • January 8, 2021 CS 21 Lecture 3 10

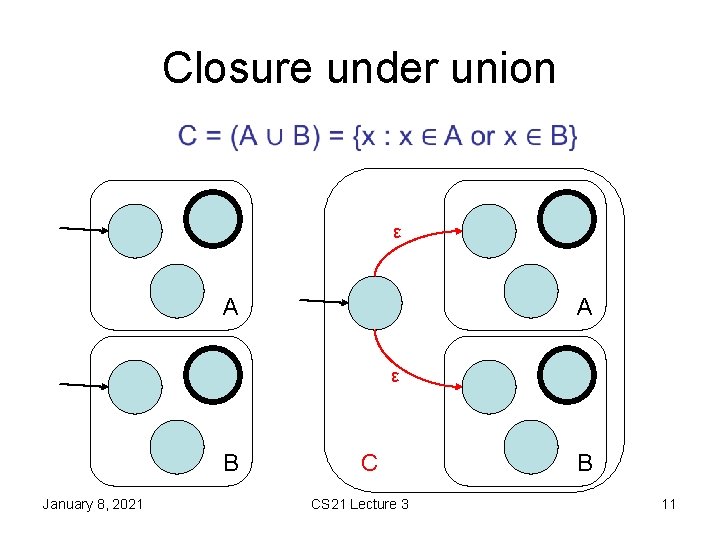
Closure under union • ε A A ε B January 8, 2021 C CS 21 Lecture 3 B 11

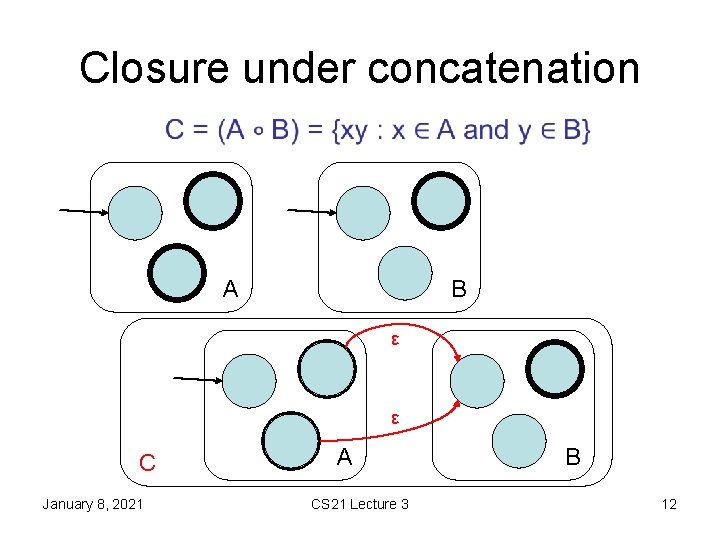
Closure under concatenation • A B ε ε C January 8, 2021 A CS 21 Lecture 3 B 12

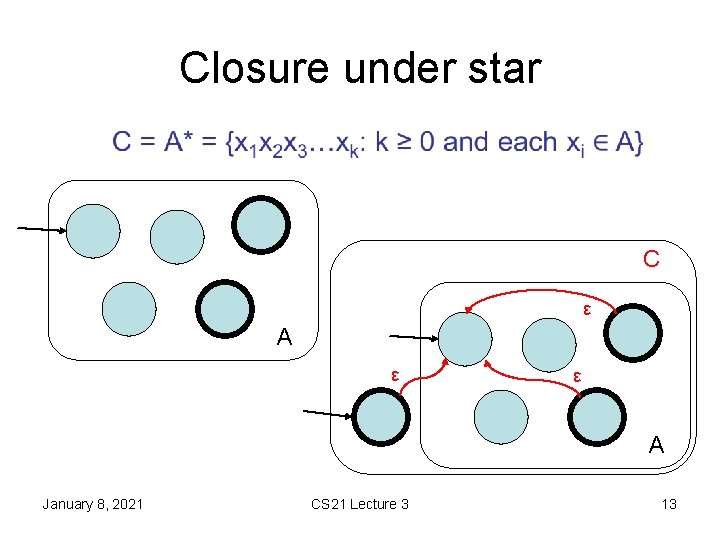
Closure under star • C ε A ε ε A January 8, 2021 CS 21 Lecture 3 13

NFA, FA equivalence • January 8, 2021 CS 21 Lecture 3 14

NFA, FA equivalence • January 8, 2021 CS 21 Lecture 3 15

NFA, FA equivalence • January 8, 2021 CS 21 Lecture 3 16

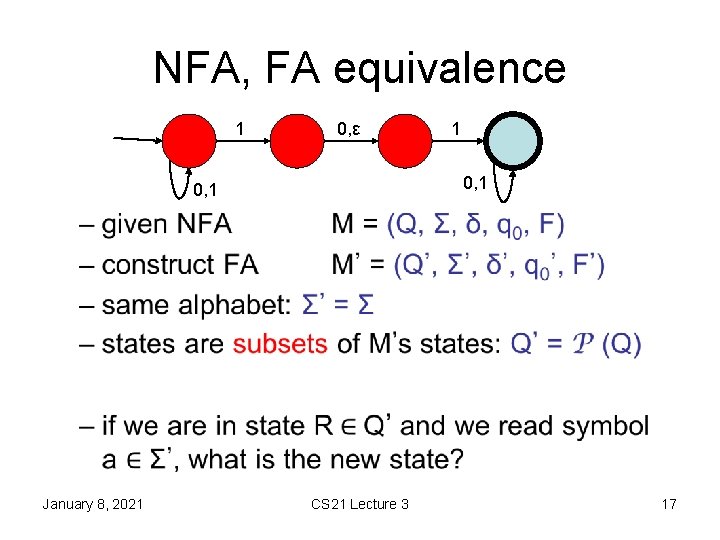
NFA, FA equivalence 1 0, ε 1 0, 1 • January 8, 2021 CS 21 Lecture 3 17

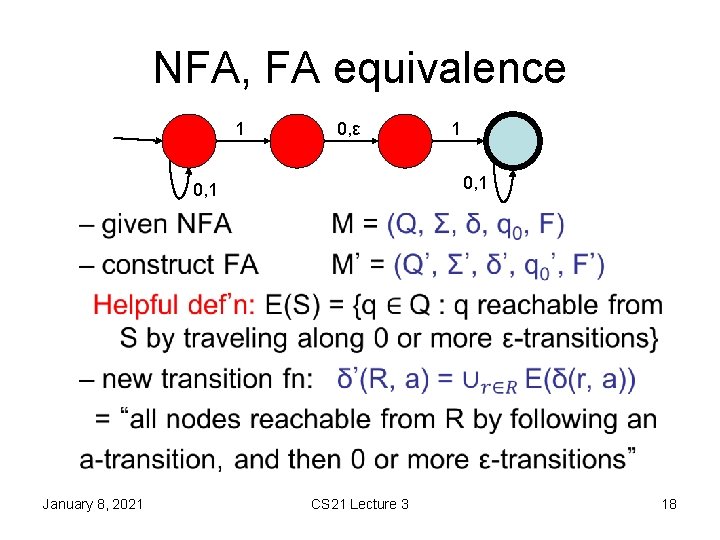
NFA, FA equivalence 1 0, ε 1 0, 1 • January 8, 2021 CS 21 Lecture 3 18

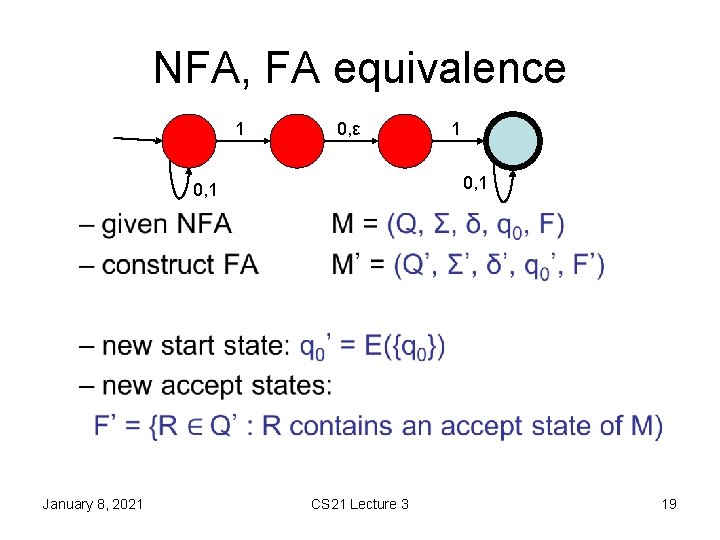
NFA, FA equivalence 1 0, ε 1 0, 1 • January 8, 2021 CS 21 Lecture 3 19

NFA, FA equivalence • January 8, 2021 CS 21 Lecture 3 20

So far… Theorem: the set of languages recognized by NFA is closed under union, concatenation, and star. Theorem: a language L is recognized by a FA if and only if L is recognized by a NFA. Theorem: the set of languages recognized by FA is closed under union, concatenation, and star. January 8, 2021 CS 21 Lecture 3 21

Next… • Describe the set of languages that can be built up from: – unions – concatenations – star operations • Called “patterns” or regular expressions • Theorem: a language L is recognized by a FA if and only if L is described by a regular expression. January 8, 2021 CS 21 Lecture 3 22

Regular expressions • January 8, 2021 CS 21 Lecture 3 23

Regular expressions • January 8, 2021 CS 21 Lecture 3 24

Some examples alphabet Σ = {0, 1} • January 8, 2021 CS 21 Lecture 3 25