CS 200 Algorithms Analysis ASYMPTOTIC NOTATION Assumes runtime


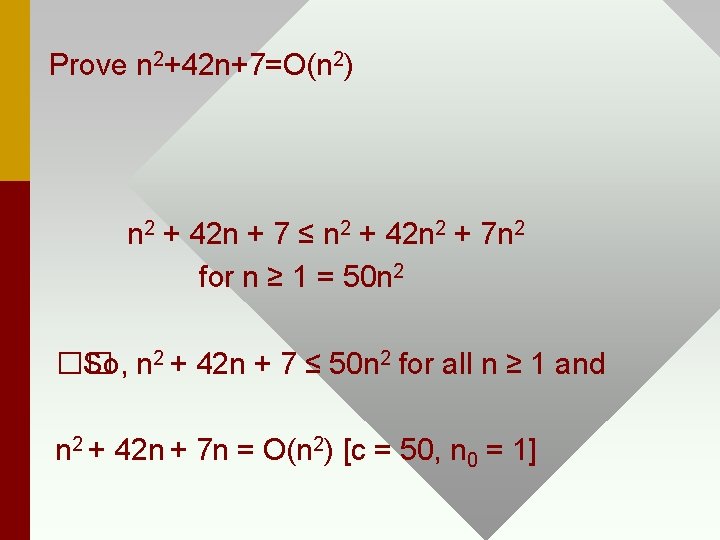














- Slides: 21

CS 200: Algorithms Analysis

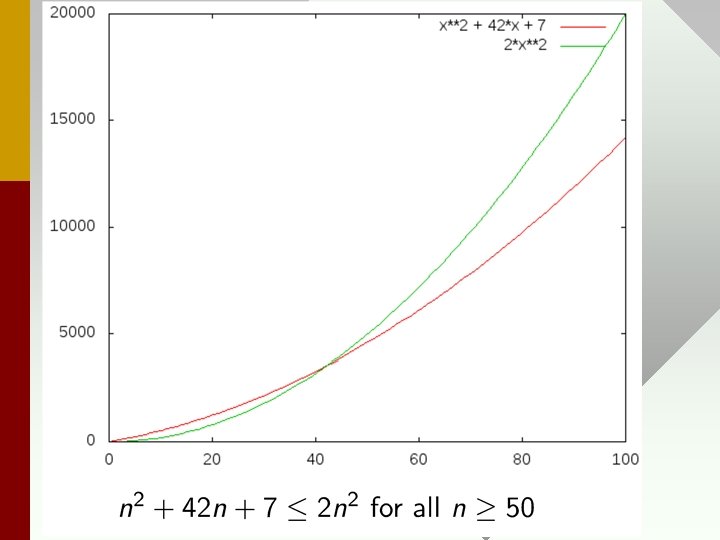
ASYMPTOTIC NOTATION • Assumes run-time of functions is N = <0, 1, 2 , . . . > • O–notation : f(n) = O(g(n)), gives an estimated upper-bound (may or may not be a tight bound) on the run-time of f(n). O(g(n)) is the set of functions: O(g(n)) = {f(n) : $ positive constants c, n 0 st 0 £ f(n) £ cg(n), " n >= n 0 • When we say f (n) = O(g(n)) we really mean f (n) ∈ O(g(n)). • Do Examples

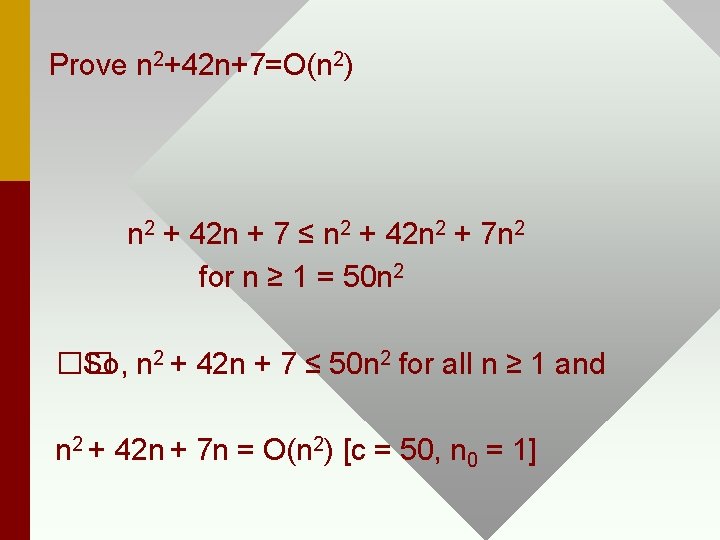
Prove n 2+42 n+7=O(n 2) n 2 + 42 n + 7 ≤ n 2 + 42 n 2 + 7 n 2 for n ≥ 1 = 50 n 2 �� So, n 2 + 42 n + 7 ≤ 50 n 2 for all n ≥ 1 and n 2 + 42 n + 7 n = O(n 2) [c = 50, n 0 = 1]

Prove 5 nlog 2 n + 8 n − 200 = O(nlog 2 n) 5 nlog 2 n + 8 n − 200 ≤ 5 nlog 2 n + 8 nlog 2 n for n ≥ 2 ≤ 13 nlog 2 n �� 5 nlog 2 n + 8 n − 200 ≤ 13 nlog 2 n for all n ≥ 2 �� 5 nlog 2 n + 8 n − 200 = O(nlog 2 n) [c = 13, n 0 = 2]

Why Use Big O Notation? Consider the following (simple) code: The �� running time is 1 assignment (int i = 0) n+1 comparisons (i < n) n increments (i++) n array offset calculations (a[i]) n indirect assignments (a[i] = i) = a+b(n+1)+cn+dn+en, where a, b, c, d, and e are constants that depend on the machine running the code �� Easier just to say O(n) operations

• O–notation is actually quite sloppy but convenient. It can be used to bound the worst-case runtime of an algorithm. Explain using insertion sort. • W–notation: f(n) = W(g(n)), gives an estimated lower-bound (may or may not be a tight bound) on the runtime of f(n). • W(g(n)) is the set of functions: W(g(n)) = {f(n) : $ positive constants c, n 0 st 0 £ cg(n) £ f(n), " n >= n 0 • Do examples

• Q–notation: f(n) = Q(g(n)), gives an estimated tight-bound on the runtime of f(n). • Q(g(n)) is the set of functions: Q(g(n)) = {f(n) : $ positive constants c 1, c 2, n 0 st 0 £ c 1 g(n) £ f(n) £ c 2 g(n), " n >= n 0 • Do examples • Obviously leading constants and lower order terms don’t matter because we can always choose constants large enough to swamp the other terms.

• Theorem: for any 2 functions f(n), g(n); f(n) = Q(g(n)) iff f(n) = O(g(n) and f(n) = W(g(n)) • This implies that we can show tight bounds from upper/lower bounds.

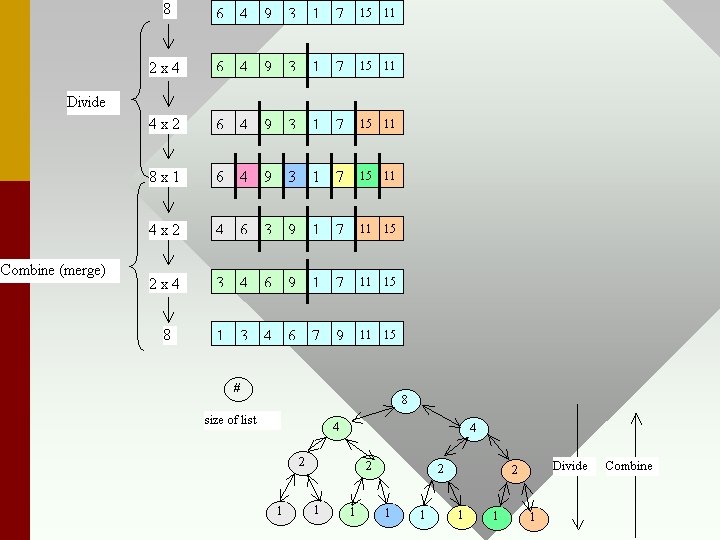
MERGESORT • Input and output are defined as for insertion sort. • Mergesort is a divide and conquer algorithm that is recursive in structure. • Divide the problem into a set of sub-problems. • Conquer by solving the sub-problems recursively. If sub-problem small enough then solve in straightforward manner. • Combine solutions to sub-problems to gain solution to original problem.

Show general recurrence for run time of Divide and Conquer algorithms. Merge. Sort Divide and Conquer • Mergesort divides an n element sequence into 2 subsequences of n/2 elements. It then sorts the 2 subsequences recursively by using Mergesort. It combines the 2 sorted subsequences via a Merge. For simplicity, assume n is a power of 2.

Merge. Sort Pseudo Code Mergesort(A, p, r) if p = r then return Mergesort(A, p, (p+r) / 2) Mergesort(A, (p+r) / 2 + 1, r) Merge results and return • What is the base case? • How do we merge two sorted subsequences? What is the run time of such a merge? Do example.

Idea behind linear-time merging: Think of two piles of cards. Each pile is sorted and placed face-up on a table with the smallest cards on top. We merge these into a single sorted pile, face-down on the table. A basic step: Choose the smaller of the two top cards. • Remove it from its pile, thereby exposing a new top card. • Place the chosen card face-down onto the output pile. Repeatedly perform basic steps until one input pile is empty. • Once one input pile empties, just take the remaining input pile and place it face-down onto the output pile. • Each basic step should take constant time, since we check just the two top cards. There are ≤ n basic steps, since each basic step removes one card from the input piles, and we started with n cards in the input piles. • Therefore, this procedure should take �� θ(n) time.


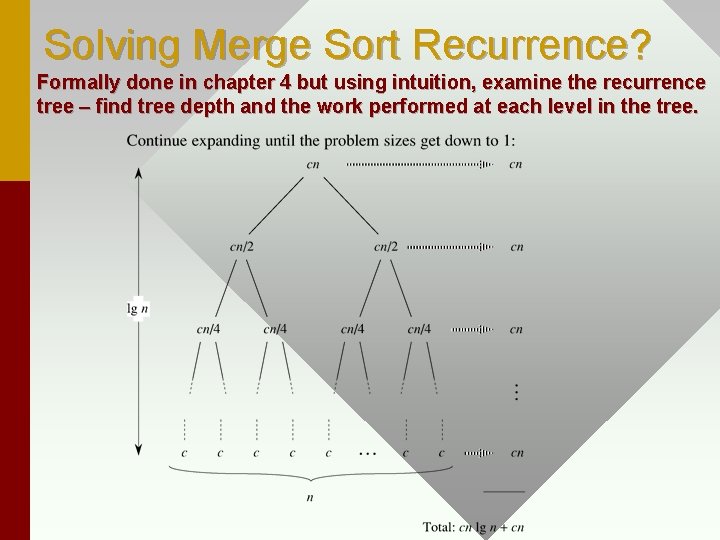
Discuss recurrence for run time of Merge. Sort. T(n) = 2 T(n/2) + θ(1) + θ(n) = 2 T(n/2) + θ(n+1) = 2 T(n/2) + θ(n) In more depth, • Do an instance of the problem. • What does the block trace (recurrence tree) look like? • Show recurrence tree for Merge. Sort.


Solving Merge Sort Recurrence? Formally done in chapter 4 but using intuition, examine the recurrence tree – find tree depth and the work performed at each level in the tree.

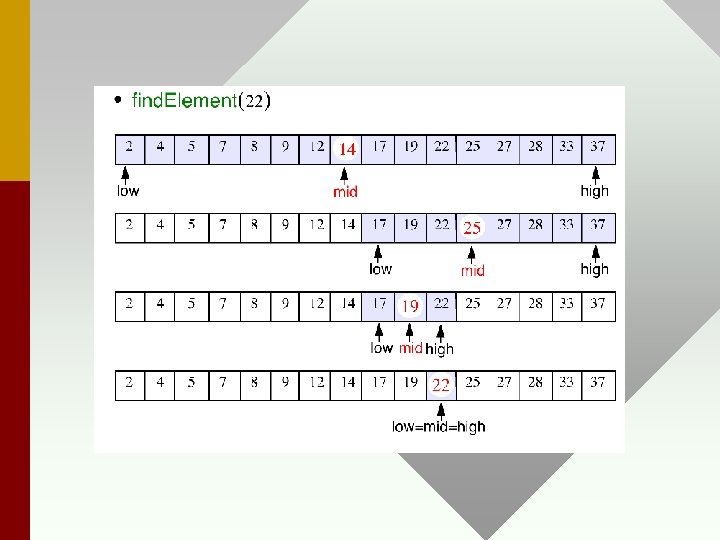
Binary Search • Recursive Binary Search of a sorted array (assume n is a power of 2)


Binary Search cont. • Divide runtime (check middle element) = ? • Conquer runtime (search upper or lower sub-array) = ? • Combine runtime (trivial) = ? • T(n) = ? = T(n/2) + θ(1) • Confirm runtime using a recurrence tree.

Summary • Definitions of Big O, Theta, and Omega • Theorem for Theta tight bounds • Application of above to simple functions • Merge. Sort/Binary Search functionality and run-time recurrences.