CS 200 Algorithm Analysis Dynamic Programming Used for

CS 200: Algorithm Analysis

Dynamic Programming • Used for optimization problems (find an optimal solution). • Technique is similar to recursive divide and conquer, but is more efficient because dynamic method does not re-compute solutions for sub-problems that have already been solved. • Dynamic programming is applied to problems that have repeated sub-problem structure (i. e computing the Fibonacci sequence) and when the solution to a subproblem is locally optimal.

• This occurs in problems that have a small sub-problem space, that is, a recursive divide and conquer algorithm for the problem would solve the same sub-problems over and over, rather than generating new sub-problems. • In such a case, the number of unique subproblems is polynomial in the input size of the problem. • The dynamic programming technique takes advantage of this sub-problem structure by solving each sub-problem only once and storing solutions in a look-up table.

Examples • Fibonnaci – html notes • Binomial Coefficients in Pascal’s Triangle– html notes • Optimal Binary Search tree – html notes • Matrix Multiply – html notes • Longest Common Subsequence – slides

Longest Common Subsequence • Given 2 sequences : x[1. . m] and y[1. . n], find a longest subsequence that is common to both of them. x : ABCBDAB y : BDCABA z : BCBA or BDAB, there is no common subsequence of length > 4.

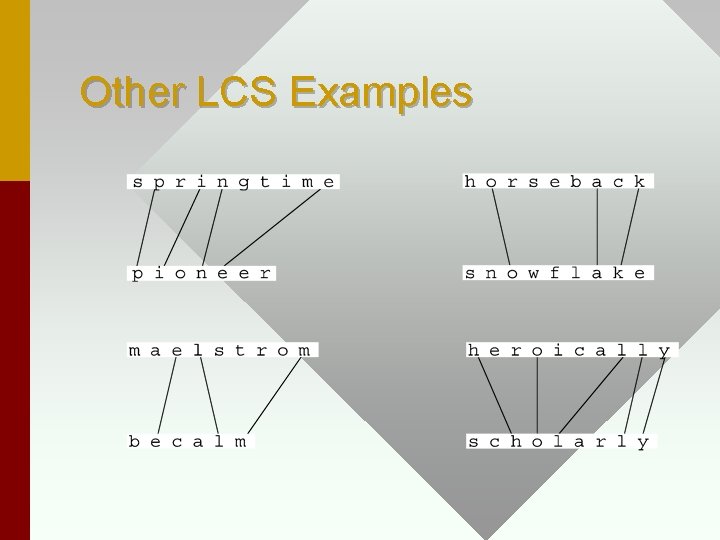
Other LCS Examples

Brute-Force Method For every subsequence of x[m], check if its a subsequence of y[n]. Since there are 2 m subsequences of x to check Example. x : 123, then possible subsequences are Ø, 1, 2, 3, 12, 13, 23, 123, which is the powerset of x. The size of the powerset of x = 2|x| and each of these subsequences must be checked by scanning all of y, the brute-force runtime is O(n 2 m).

Definition of power-set - if S is a set and |S| = m then the power-set of S is all subsets of S including S and Ø set. The cardinality of the power-set of S is 2 m. The runtime for the brute force method is obviously unattractive, since it is exponential. A better method uses Dynamic Programming techniques. The following discussion examines only the lengths of common subsequences and not the actual sequences – simple extension later. C is used to hold the length of the longest subsequence.

Definition of Longest Common Subsequence Problem for x[1. . m] and y[1. . n]. Dfn: C[i, j] = 0 if i=0 or j = 0 Ex. x : ABA , y : BA Then C[1, 1] = 0, C[1, 2] = 1, C[2, 1] = 1, C[3, 1] = 1, C[2, 2] = 1, C[3, 2] = 2.

Recursive Formulation

Recursive Formulation

Recursive Formulation

Recursive Formulation

Recursive Formulation

Dynamic Programming Hallmark #1

Recursive Algorithm for LCS

Recursive Algorithm for LCS

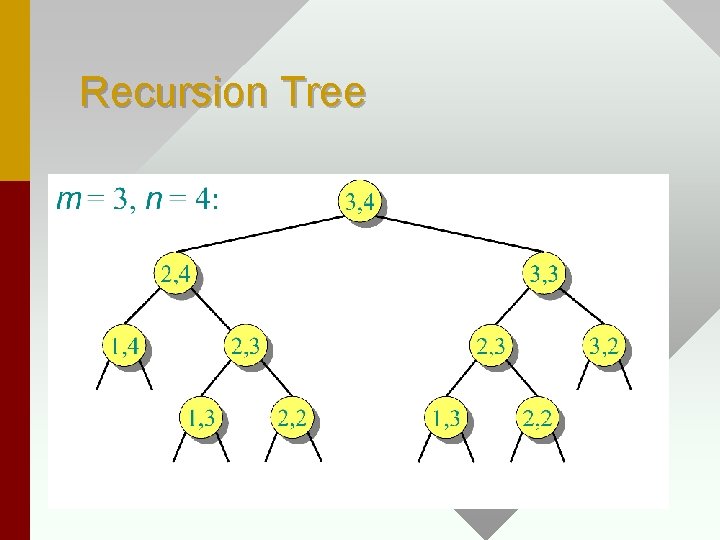
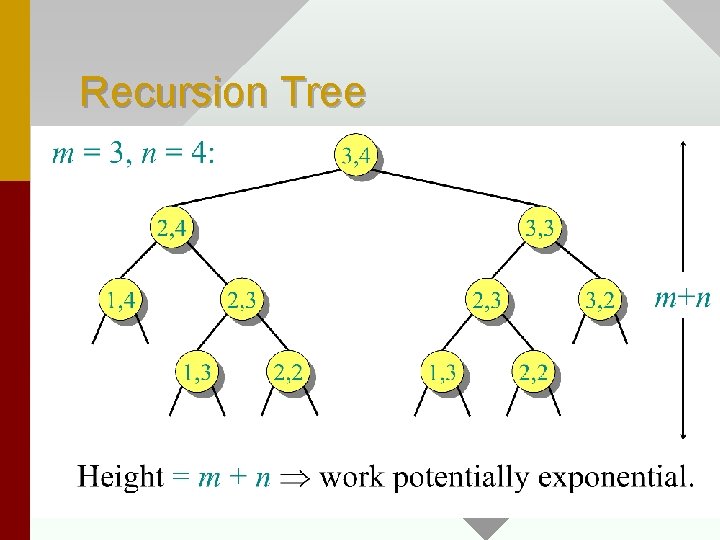
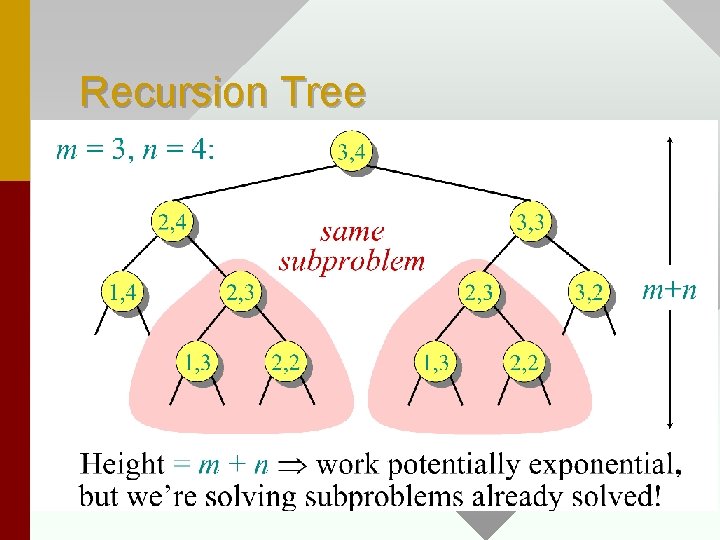
Recursion Tree

Recursion Tree

Recursion Tree

Dynamic Programming Hallmark #2

Memoization

• MEMOIZE TECHNIQUE: Deals with memorizing overlapping sub-problems by storing them in a look-up table (merely an array of solutions to subproblems). • A memoize technique is very similar to dynamic programming (both use table look-up), but a memoize algorithm has recursion as its control structure and is a top down algorithm while dynamic programming uses iteration as its control structure and is a bottom up algorithm. • Dynamic programming therefore does not incur the overhead of recursion.

Memoization

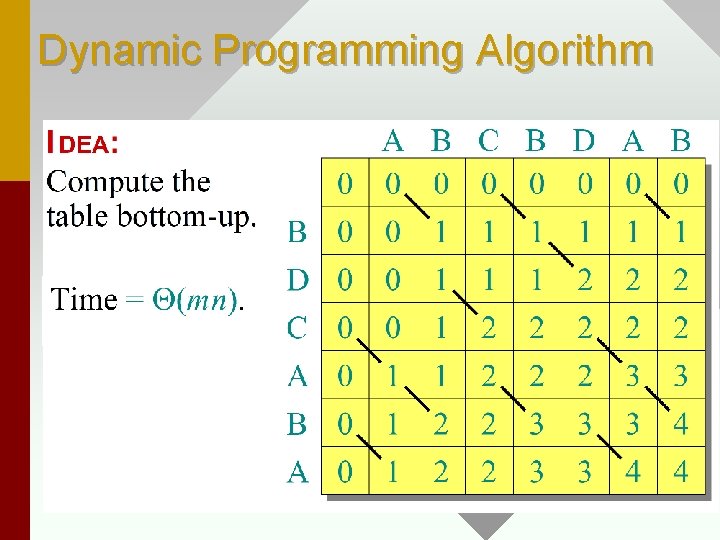
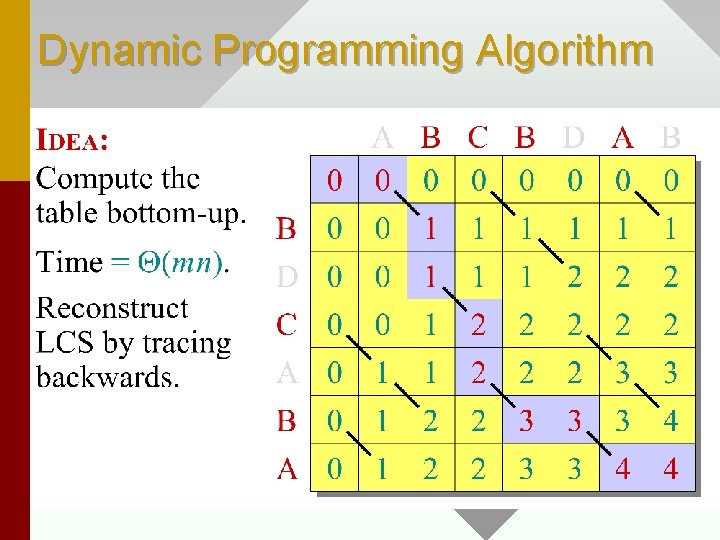
Dynamic Programming Algorithm

Dynamic Programming Algorithm

Dynamic Programming Algorithm

LCS_Length(x, y) for i = 0 to m do c[i, 0] = 0; for j = 0 to n do c[0, j] = 0; for i = 1 to m do for j = 1 to n do if x[i] = y[j] then c[i, j] = c[i-1, j-1] + 1; b[i, j] = ''; else if c[i-1, j] >= c[i, j-1] c[i, j] = c[i-1, j]; b[i, j] = '|'; else c[i, j] = c[i, j-1]; b[i, j] = '–';

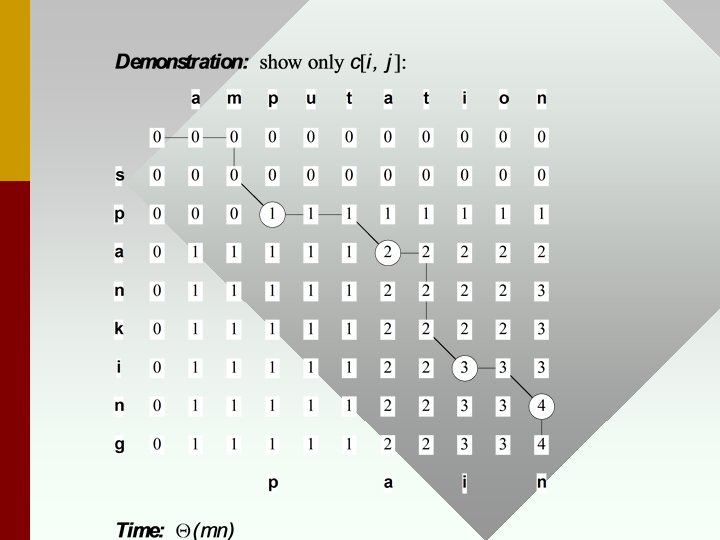
• Length of LCS is number at bottom right of Table. • Trace backwards following arrows to reconstruct LCS. A diagonal arrow => add to sequence. • Space used for this technique ______? • Homework exercise asks you to reduce size of table to Q(min(m, n)) by keeping only necessary info around.

Summary • Dynamic Programming – optimal solution, locally optimal subproblems • Longest Common Subsequence Problem