CS 200 Algorithm Analysis BINARY SEARCH TREES Important

CS 200: Algorithm Analysis

BINARY SEARCH TREES Important data structure for dynamic sets – dictionary or priority queue. Many BST operations are performed in O(h) where h is height of tree. Node in tree is a record with 5 fields : pointer to parent node, pointer to left/right child, key and data. Do example tree that stores characters in lexicographical or numerical order (next slide).

Root? Leaf? Interior Node? Parent/child? Sub-tree? This nearly complete BST is well balanced –> log n runtimes.

Another well balanced example.

An unbalanced BST giving linear runtimes.

BINARY SEARCH TREE PROPERTY: 1. if y is left sub-tree of x then key[y] <= key[x]. 2. if y is right sub-tree of x then key[y] > key[x]. Pulling keys out of tree in sorted order requires an INORDER walk of the tree.

Inorder. Tree. Walk(x) //start at root if x != null then Inorder. Tree. Walk(Left[x]) print(key[x]) Inorder. Tree. Walk(Right[x]) • Show sequence of output using example tree. ABDFHK. Do walk. • Runtime of tree walk with an n-node BST ?

Other operations : Searching and Insertion. Where is minimum? maximum? Tree. Search(x, k) //x starts at root, k is key if (x = nil) or (k = key[x]) then return x else if k < key[x] then return Tree. Search(left[x], k) else return Tree. Search(right[x], k) • Trace algorithm by searching for 4 and 10 in example tree. If k is not in tree then return nil.

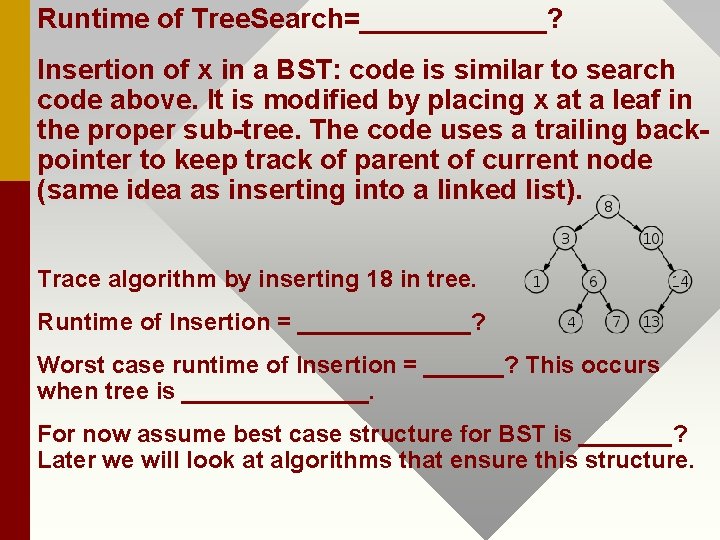
Runtime of Tree. Search=______? Insertion of x in a BST: code is similar to search code above. It is modified by placing x at a leaf in the proper sub-tree. The code uses a trailing backpointer to keep track of parent of current node (same idea as inserting into a linked list). Trace algorithm by inserting 18 in tree. Runtime of Insertion = _______? Worst case runtime of Insertion = ______? This occurs when tree is _______. For now assume best case structure for BST is _______? Later we will look at algorithms that ensure this structure.

SORTING OF BST’s Sort(A) for i = 1 to n do Tree. Insert(A[i]) Inorder. Tree. Walk(root) Do example trace of algorithm. Notice similarity to Quicksort’s Partition algorithm. In this case though, no reordering of partition elements occurs. Each element requires same comparisons as in Quicksort but in a different order.

Discuss the comparisons made for the example trace. Since the runtime is proportional to # of comparisons made, the average time is the same as Quicksort = O(n logn). Quicksort is better: in place sort, no additional data structure, small constants.

BST OPERATIONs Minimum (maximum) is a required operation for priority queues. BST as a priority queue implements minimum as: Tree. Minimum(x) //x is pointer to root while left[x] != null then x = left[x] return x Runtime for tree minimum ?

Successor operation retrieves successor node of x. Successor node of x is node with key that immediately follows the key of x, in sorted order. Tree. Successor(x) if right[x] != null then{if right, suc. is min in subtree} return Tree. Minimum(right[x]) y = parent[x] while(y!=null) and(x=right[y]) do x=y y =parent[y] return y {else suc. is back up tree to left of parent}

Tree. Successor(x) if right[x] != null then return Tree. Minimum(right[x]) y = parent[x] while(y!=null) and(x=right[y]) do x=y y =parent[y] return y

Do an example trace of algorithm Runtime of Tree. Successor = ____? Note that predecessor algorithm is analogous.

Deletion operation removes a node from the tree. The following is a very informal pseudo code for operation. Tree. Delete(T, x) if x has no children then {case 0} remove x if x has one child then {case 1} make parent[x] point to child remove x if x has two children then {case 2] swap x with its successor perform case 0 or 1 to delete it

Do example trace for three cases of algorithm. See code next slide. Note: the above swap could also be done with predecessor. Runtime of Delete operation ?

D or A

Minimizing runtimes: • Problem: the worst case for operations on BST are ______, which is no better than using a linked list representation for a priority queue. • Solution: guarantee that the BST is balanced which minimizes its height. Method: restructure tree when necessary. Nothing special required for query operations but extra work needed when tree is modified via an insert or delete operation.

Summary • BST properties – algorithms and run-times • BST sorting

Do BST Activity in pairs.