CS 2 in C Peer Instruction Materials by

CS 2 in C++ Peer Instruction Materials by Cynthia Bailey Lee is licensed under a Creative Commons Attribution-Non. Commercial. Share. Alike 4. 0 International License. Permissions beyond the scope of this license may be available at http: //peerinstruction 4 cs. org. CS 106 X – Programming Abstractions in C++ Cynthia Bailey Lee

2 Today’s Topics: Heaps! 1. Binary heaps 2. 3. Insert, delete Reasoning about outcomes in Binary heaps, and Big O analysis Heapsort algorithm (Schedule note: we’ll save stack and queue implementation for another day…)

Binary heap insert and delete
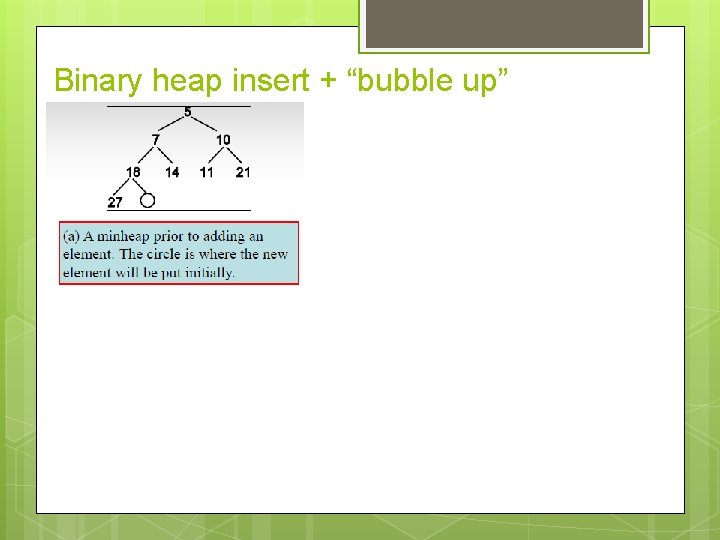
Binary heap insert + “bubble up”
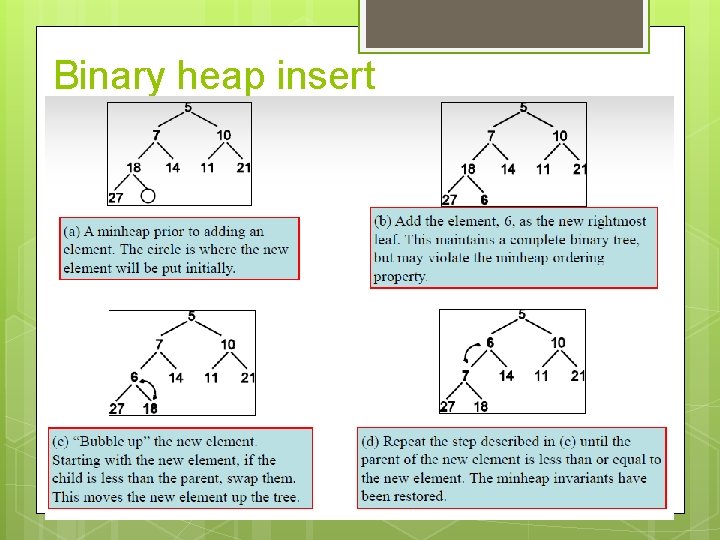
Binary heap insert
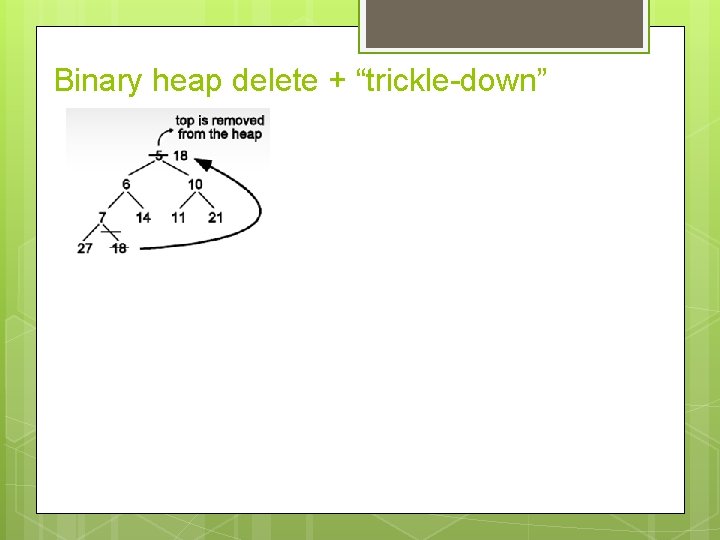
Binary heap delete + “trickle-down”
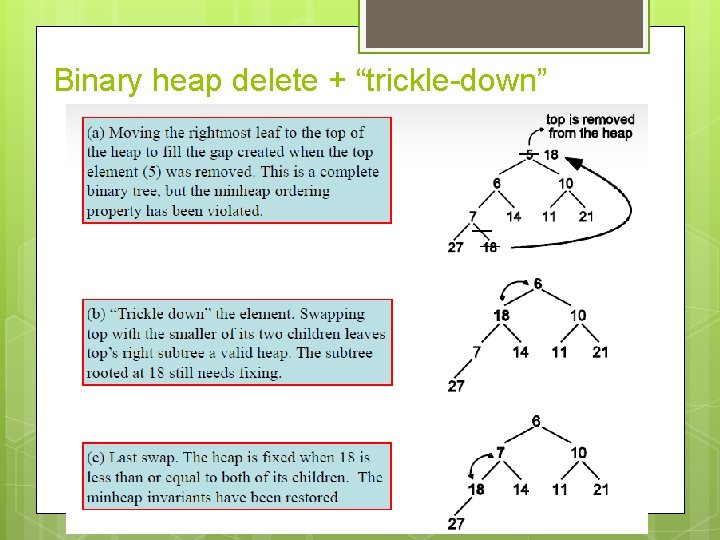
Binary heap delete + “trickle-down”

Heap outcomes by insert order Create a MIN heap by inserting the elements, one by one, in the order given below for the second letter of your first name: A-F: {3, 9, 18, 22, 34} G-L: {3, 22, 18, 9, 34} M-R: {9, 22, 18, 3, 34} S-Z: {18, 22, 3, 9, 34}

TRUE OR FALSE There is only one configuration of a valid minheap containing the elements {34, 22, 3, 9, 18} A. B. TRUE FALSE

Heap outcomes by insert order Create a MIN heap by inserting the elements, one by one, in the order given below for the first letter of your last name: A-F: {18, 9, 34, 3, 22} G-L: {3, 18, 22, 9, 34} M-R: {22, 9, 34, 3, 18} S-Z: {34, 3, 9, 18, 22}

How many distinct min-heaps are possible for the elements {3, 9, 18, 22, 34}? A. B. C. D. E. 1 -2 3 -4 5 -8 5! (5 factorial) Other/none/more

Time cost What is the worst-case time cost for each heap operation: Add, Remove, Peek? A. B. C. D. E. O(n), O(1) O(logn), O(1), O(logn) O(n), O(logn) Other/none/more

Heapsort

Heapsort is super easy 1. 2. Insert unsorted elements one at a time into a heap until all are added Remove them from the heap one at a time (we will always be removing the next biggest item, for max-heap; or next smallest item, for min-heap) THAT’S IT!

Implementing heapsort Devil’s in the details
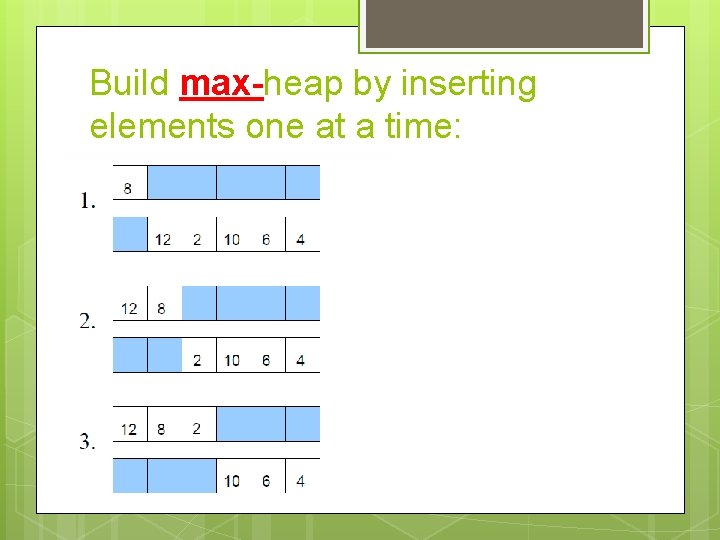
Build max-heap by inserting elements one at a time:
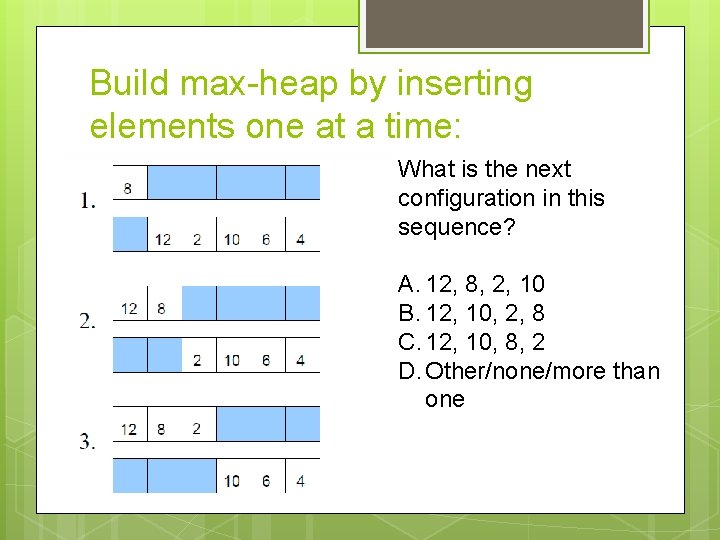
Build max-heap by inserting elements one at a time: What is the next configuration in this sequence? A. 12, 8, 2, 10 B. 12, 10, 2, 8 C. 12, 10, 8, 2 D. Other/none/more than one
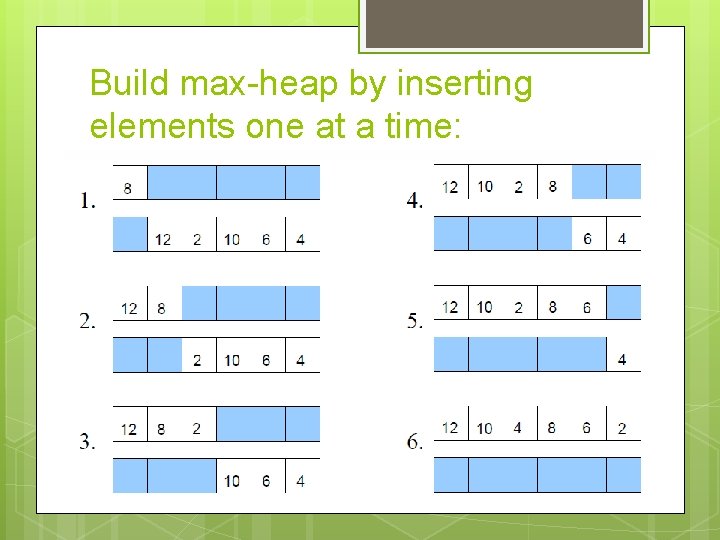
Build max-heap by inserting elements one at a time:
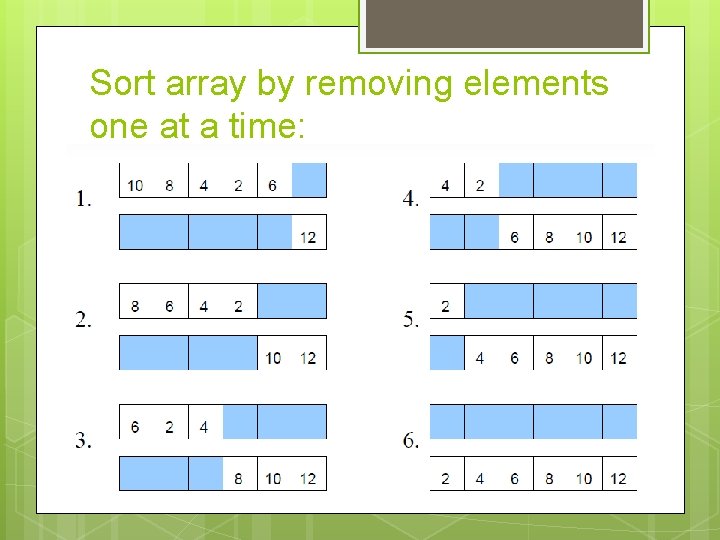
Sort array by removing elements one at a time:
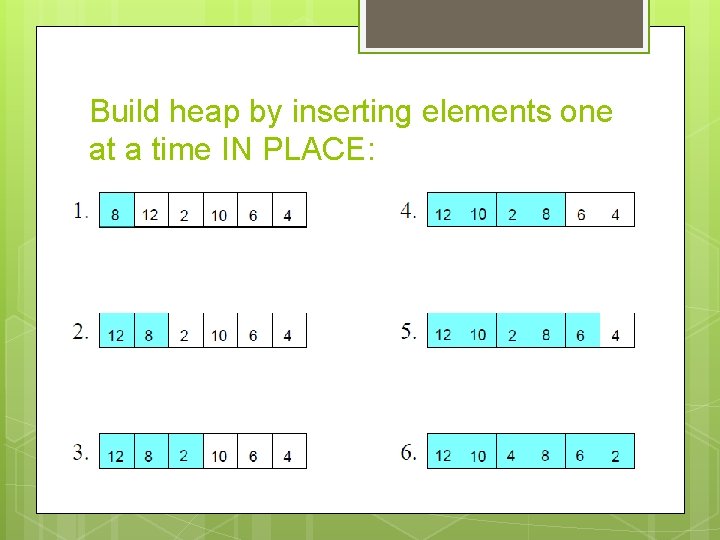
Build heap by inserting elements one at a time IN PLACE:

Sort array by removing elements one at a time IN PLACE:

Complexity How many times do we do insert() when building the heap? How much does each cost? How many times do we delete-max() when doing the final sort? How much does each cost?
- Slides: 22