CS 188 Artificial Intelligence Spring 2007 Lecture 16

CS 188: Artificial Intelligence Spring 2007 Lecture 16: Review 3/8/2007 Srini Narayanan – ICSI and UC Berkeley

Midterm Structure § 5 questions § § § § § Search (HW 1 and HW 2) CSP (Written 2) Games (HW 4) Logic (HW 3) Probability/BN (Today’s lecture) One page cheat sheet and calculator allowed. Midterm weight: 15% of your total grade. Today Review 1: Mostly Probability/BN Sunday: Review 2: All topics review and Q/A

Probabilities § What you are expected to know § Basics § § Conditional and Joint Distributions Bayes Rule Converting from conditional to joint and vice-versa Independence and conditional independence § Graphical Models/Bayes Nets § § Building nets from descriptions of problems Conditional Independence Inference by Enumeration from the net Approximate inference (Prior sampling, rejection sampling, likelihood weighting)

Review: Useful Rules § Conditional Probability (definition) § Chain Rule § Bayes Rule

Marginalization § Marginalization (or summing out) is projecting a joint distribution to a sub-distribution over subset of variables T P P warm 0. 5 cold 0. 5 T S warm sun 0. 4 warm rain 0. 1 cold sun 0. 2 S cold rain 0. 3 sun 0. 6 rain 0. 4 P

The Product Rule § Sometimes joint P(X, Y) is easy to get § Sometimes easier to get conditional P(X|Y) § Example: P(sun, dry)? R P sun 0. 8 rain 0. 2 D S P wet sun 0. 1 wet sun 0. 08 dry sun 0. 9 dry sun 0. 72 wet rain 0. 7 wet rain 0. 14 dry rain 0. 3 dry rain 0. 06

Conditional Independence § Reminder: independence § X and Y are independent ( ) iff or equivalently, § X and Y are conditionally independent given Z ( ) iff or equivalently, § (Conditional) independence is a property of a distribution

Conditional Independence § For each statement about distributions over X, Y, and Z, if the statement is not always true, state a conditional independence assumption which makes it true. § § § P(x|y) = P(x, y) / p(y) P(x, y) = P(x)P(y) P(x, y, z) = P(x|z)P(y|z)P(z) P(x, y, z) = P(x)P(y)P(z|x, y) P(x, y) = Sumz (x, y, z)

Conditional Independence § For each statement about distributions over X, Y , and Z, if the statement is not always true, state a conditional independence assumption which makes it true. § P(x|y) = P(x, y)/ P(y) § always true § P(x, y) = P(x)P(y) § true if x and y are independent § P(x, y, z) = P(x|z)P(y|z)P(z) § true if x and y and independent given z § P(x, y, z) = P(x)P(y)P(z|x, y) § true if x and y are independent § P(x, y) = Sumz (x, y, z) § always true

Conditional and Joint Distributions § Suppose I want to determine the joint distribution § P (W, X, Y, Z). § Assume I know § P(X, Y, Z) and P(W |X, Y) § What assumptions do I need to make to compute P(W, X, Y, Z)?

Conditional and Joint Distributions § Suppose I want to determine the joint distribution § P (W, X, Y, Z). § Assume I know § P(X, Y, Z) and P(W | X, Y) § What assumptions do I need to make to compute P(W, X, Y, Z)? § ANS: § P(X, Y, Z, W) = P(X, Y, Z| W) P(W) = P(W |X, Y, Z) P(X, Y, Z) § If I assume P(W | X, Y, Z) = P (W | X, Y) ie. W is independent of Z given both X and Y, I can compute the joint.

Graphical Model Notation § Nodes: variables (with domains) § Can be assigned (observed) or unassigned (unobserved) § Arcs: interactions § Similar to CSP constraints § Indicate “direct influence” between variables § arrows from a to b means b “depends on” a. Often the arrows indicate causation

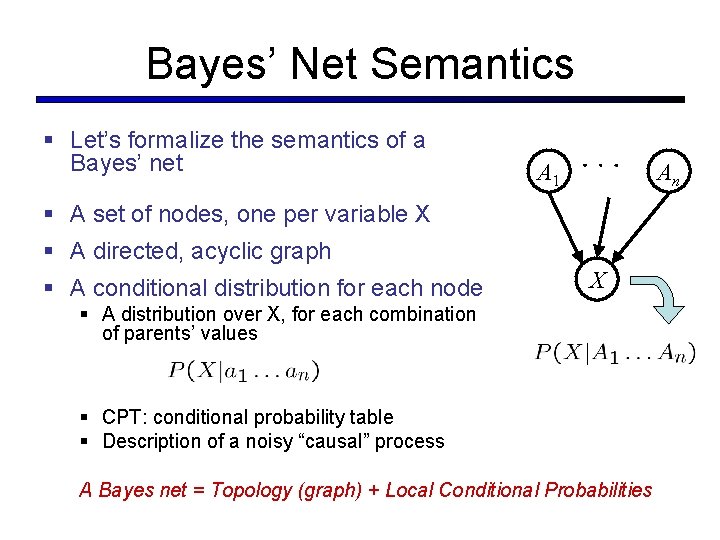
Bayes’ Net Semantics § Let’s formalize the semantics of a Bayes’ net A 1 An § A set of nodes, one per variable X § A directed, acyclic graph § A conditional distribution for each node X § A distribution over X, for each combination of parents’ values § CPT: conditional probability table § Description of a noisy “causal” process A Bayes net = Topology (graph) + Local Conditional Probabilities

Probabilities in BNs § Bayes’ nets implicitly encode joint distributions § As a product of local conditional distributions § To see what probability a BN gives to a full assignment, multiply all the relevant conditionals together: § Example: § This lets us reconstruct any entry of the full joint § Not every BN can represent every full joint § The topology enforces certain conditional independencies

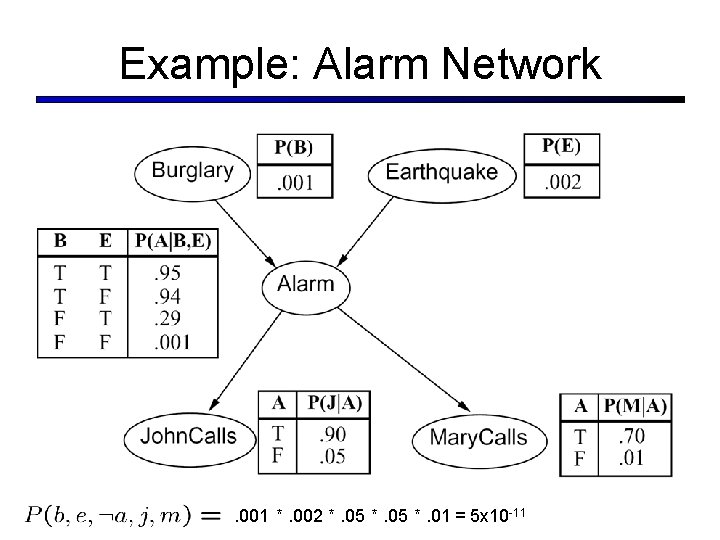
Example: Alarm Network . 001 *. 002 *. 05 *. 01 = 5 x 10 -11

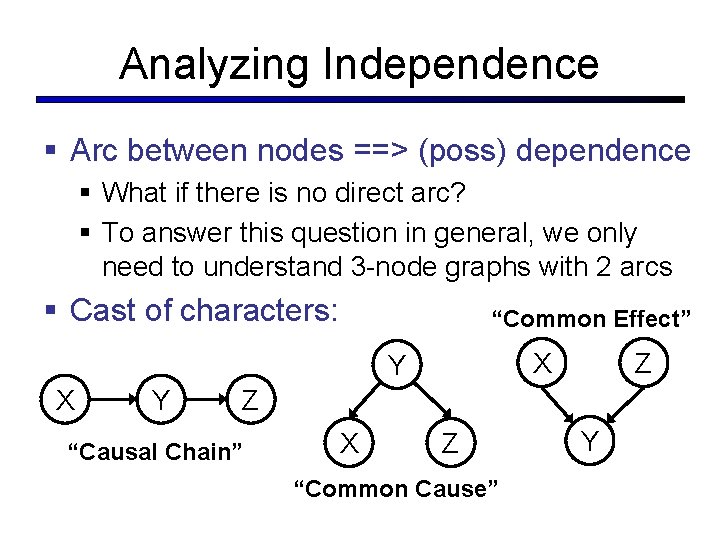
Analyzing Independence § Arc between nodes ==> (poss) dependence § What if there is no direct arc? § To answer this question in general, we only need to understand 3 -node graphs with 2 arcs § Cast of characters: “Common Effect” X Y Z Z “Causal Chain” X Z “Common Cause” Y

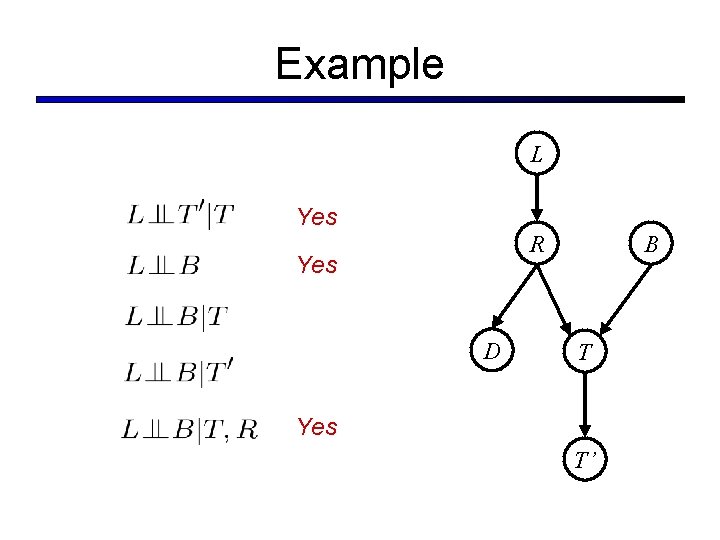
Example L Yes R Yes D B T Yes T’

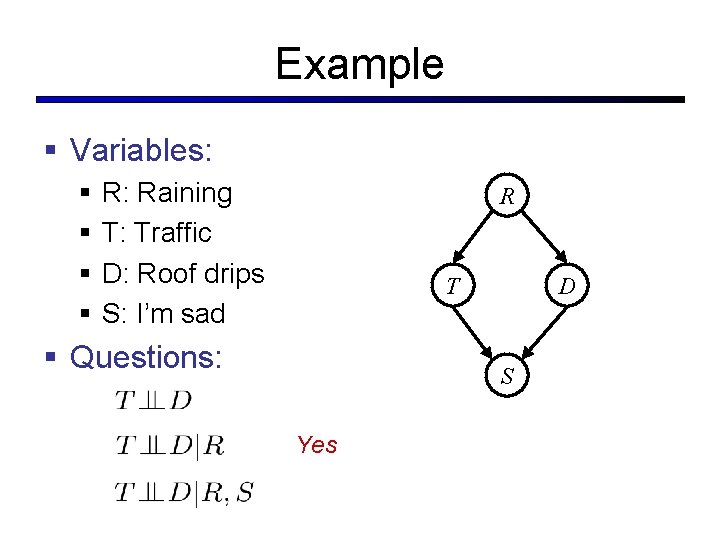
Example § Variables: § § R: Raining T: Traffic D: Roof drips S: I’m sad R T § Questions: D S Yes

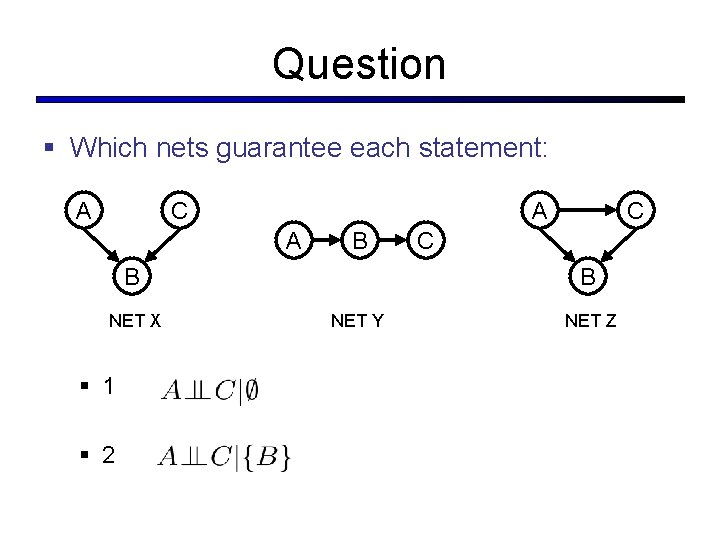
Question § Which nets guarantee each statement: A C A A B B NET X § 1 § 2 C C B NET Y NET Z

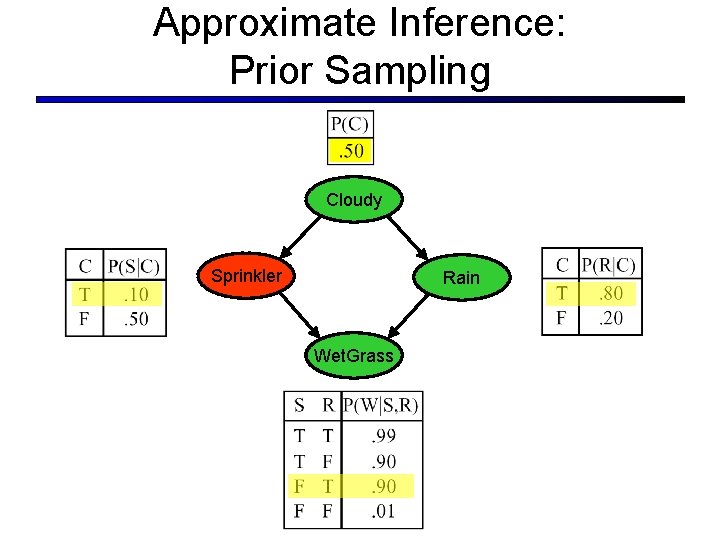
Approximate Inference: Prior Sampling Cloudy Sprinkler Rain Wet. Grass

Example § We’ll get a bunch of samples from the BN: c, s, r, w c, s, r, w c, s, r, w c, s, r, w Cloudy C Sprinkler S Rain R Wet. Grass W § If we want to know P(W) § § § We have counts <w: 4, w: 1> Normalize to get P(W) = <w: 0. 8, w: 0. 2> This will get closer to the true distribution with more samples Can estimate anything else, too What about P(C| r)? P(C| r, w)?

Rejection Sampling Cloudy C § Let’s say we want P(C| s) § Same thing: tally C outcomes, but ignore (reject) samples which don’t have S=s § This is rejection sampling § It is also consistent (correct in the limit) Sprinkler S Rain R Wet. Grass W c, s, r, w c, s, r, w c, s, r, w c, s, r, w

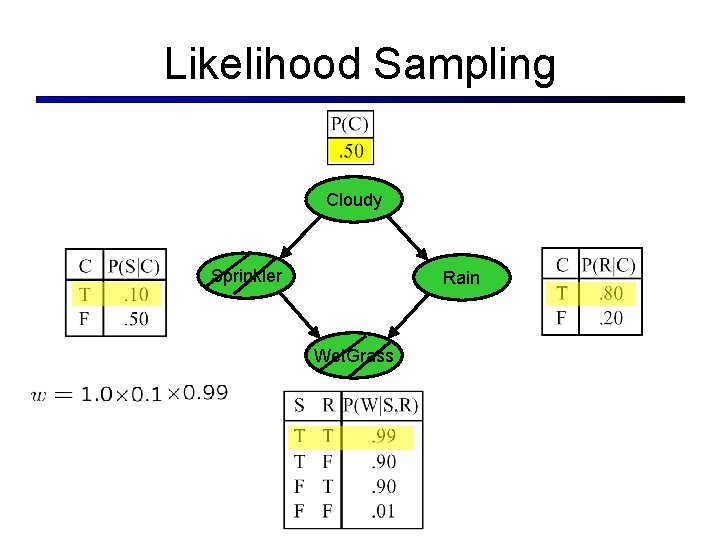
Likelihood Weighting § Problem with rejection sampling: § If evidence is unlikely, you reject a lot of samples § You don’t exploit your evidence as you sample § Consider P(B|a) Burglary Alarm § Idea: fix evidence variables and sample the rest Burglary Alarm § Problem: sample distribution not consistent! § Solution: weight by probability of evidence given parents

Likelihood Sampling Cloudy Sprinkler Rain Wet. Grass

Design of BN § When designing a Bayes net, why do we not make every variable depend on as many other variables as possible?

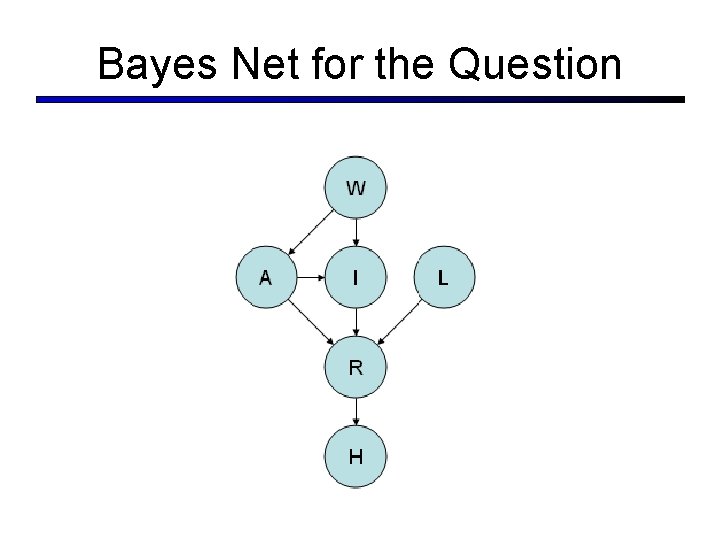
Design of a BN § You are considering founding a startup to make AI based robots to do household chores, and you want to reason about your future. There are three ways you can possibly get rich (R), either your company can go public via an IPO (I), it can be acquired (A), or you can win the lottery (L). Your company cannot go public if it gets acquired. Of course, in order for your company to either go public or get acquired, your robot has to actually work (W). You decide that if you do strike it rich then you will probably retire to Hawaii (H) to live the good life. § Draw a graphical model for the problem that reflects the causal structure as stated.

Bayes Net for the Question

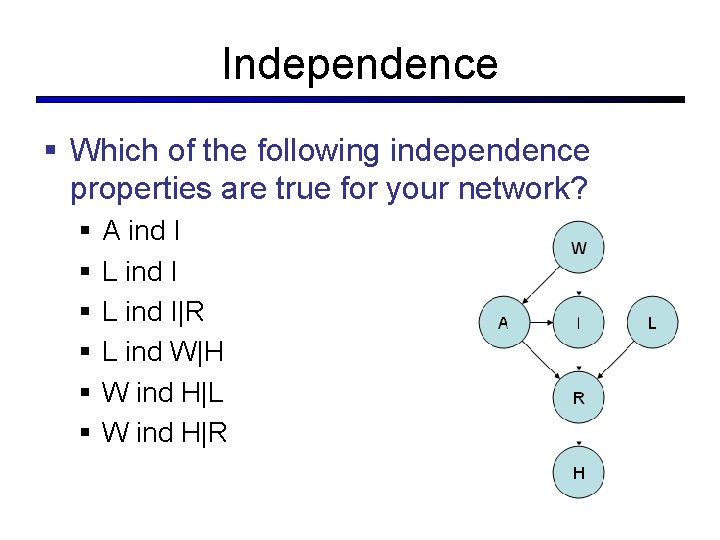
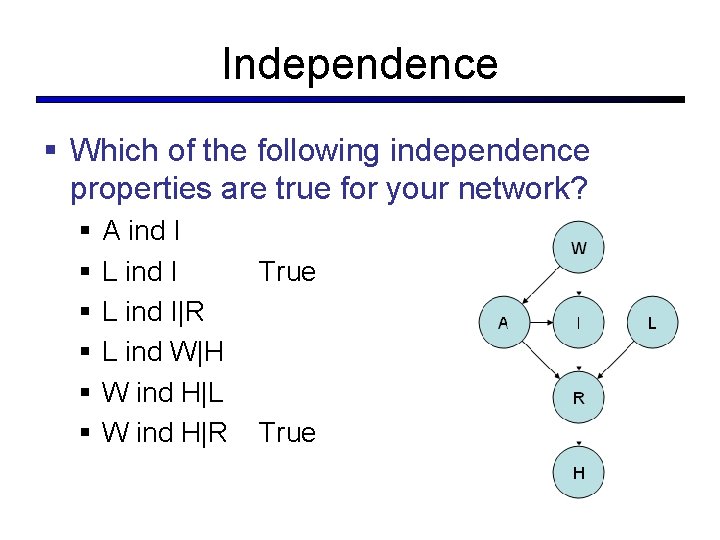
Independence § Which of the following independence properties are true for your network? § § § A ind I L ind I|R L ind W|H W ind H|L W ind H|R

Independence § Which of the following independence properties are true for your network? § § § A ind I L ind I|R L ind W|H W ind H|L W ind H|R True

Inference § Write out an expression for an entry § P(a, h, i, l, r, w), of the joint distribution encoded by your network, P(A, H, I, L, R, W) in terms of quantities provided by the network.

Inference § Write out an expression for an entry § P(a, h, i, l, r, w), of the joint distribution encoded by your network, P(A, H, I, L, R, W) in terms of quantities provided by the network. § P(a, h, i, l, r, w) = § P(w)P(a|w)P(i|w, a)P(r|a, i, l)P(h|r)

The three prisoners § § § Three prisoners A, B, and C have been tried for murder. Their verdicts will be read and sentence executed tomorrow. They know that only one of them will be declared guilty and hanged, the other two will be set free. § The identity of the guilty prisoner is not known to the prisoners, only to a prison guard. § In the middle of the night, prisoner A calls the guard over and makes the following request. § A to Guard: Please take this letter to one of my friends, the one who is to be released. You and I know that at least one of the others (B, C) will be freed. § The guard agrees. § An hour later, A calls the guard and asks “Can you tell me which person (B or C) you gave the letter to. This should give me no clue about my chances since either of them had an equal chance of receiving the letter. ” § The guard answers “I gave the letter to B. B will be released tomorrow. ” § A thinks “Before I talked to the guard, my chances of being executed were 1 in 3. Now that he has told me that B will be released, only C and I remain, so my chances are 1 in 2. What did I do wrong? I made certain not to ask for any information relevant to my own fate. . Question: What is A’s chance of perishing at dawn. 1 in 2 or 1 in 3. Why?

Topic Review § § Search CSP Games Logic

Search § Uninformed Search § DFS, BFS § Uniform Cost § Iterative Deepening § Informed Search § Best first greedy § A* § Admissibility § Consistency § Coming up with admissible heuristics § relaxed problem § Local Search

CSP § § § Formulating problems as CSPs Basic solution with DFS with backtracking Heuristics (Min Remaining Value, LCV) Forward Checking Arc consistency for CSP

Games § Problem formulation § Minimax and zero sum two player games § Alpha-Beta pruning

Logic § Basics: Entailment, satisfiability, validity § Prop Logic § Truth tables, enumeration § converting propositional sentences to CNF § Propositional resolution § First Order Logic § Basics: Objects, relations, functions, quantifiers § Converting NL sentences into FOL

Search Review § Uninformed Search § DFS, BFS § Uniform Cost § Iterative Deepening § Informed Search § Best first greedy § A* § Admissible § Consistency § Relaxed problem for heuristics § Local Search

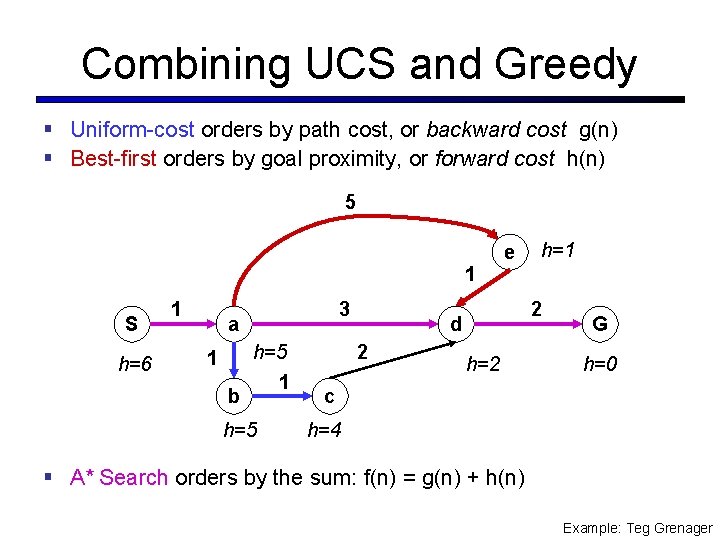
Combining UCS and Greedy § Uniform-cost orders by path cost, or backward cost g(n) § Best-first orders by goal proximity, or forward cost h(n) 5 1 S h=6 1 3 a 1 b h=5 1 h=5 e 2 d 2 h=1 h=2 G h=0 c h=4 § A* Search orders by the sum: f(n) = g(n) + h(n) Example: Teg Grenager

Admissible Heuristics § A heuristic is admissible (optimistic) if: where is the true cost to a nearest goal § E. g. Euclidean distance on a map problem § Coming up with admissible heuristics is most of what’s involved in using A* in practice.

Trivial Heuristics, Dominance § Dominance: § Heuristics form a semi-lattice: § Max of admissible heuristics is admissible § Trivial heuristics § Bottom of lattice is the zero heuristic (what does this give us? ) § Top of lattice is the exact heuristic

Constraint Satisfaction Problems § Standard search problems: § State is a “black box”: any old data structure § Goal test: any function over states § Successors: any map from states to sets of states § Constraint satisfaction problems (CSPs): § State is defined by variables Xi with values from a domain D (sometimes D depends on i) § Goal test is a set of constraints specifying allowable combinations of values for subsets of variables § Simple example of a formal representation language § Allows useful general-purpose algorithms with more power than standard search algorithms

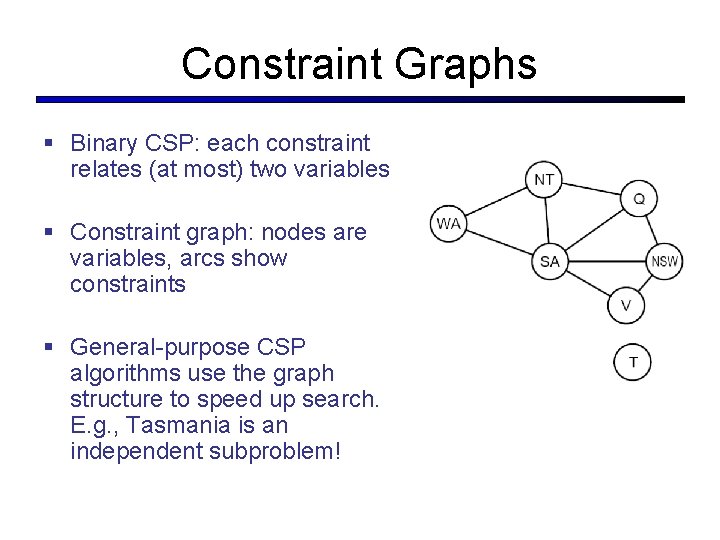
Constraint Graphs § Binary CSP: each constraint relates (at most) two variables § Constraint graph: nodes are variables, arcs show constraints § General-purpose CSP algorithms use the graph structure to speed up search. E. g. , Tasmania is an independent subproblem!

Improving Backtracking § General-purpose ideas can give huge gains in speed: § § Which variable should be assigned next? In what order should its values be tried? Can we detect inevitable failure early? Can we take advantage of problem structure?

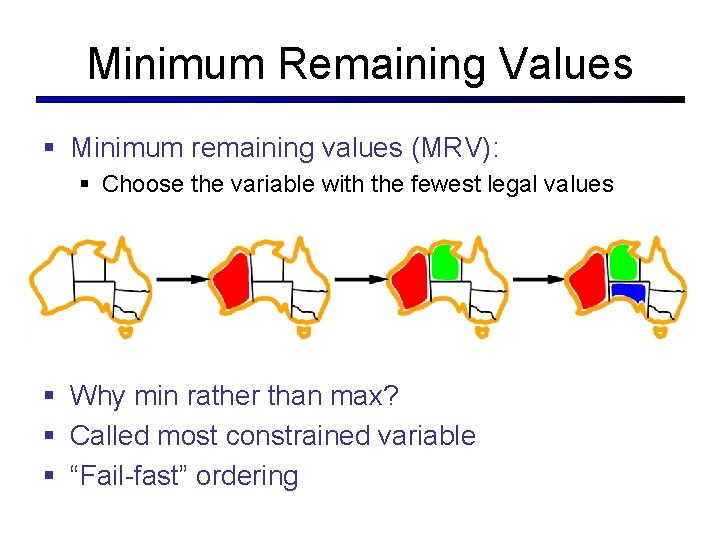
Minimum Remaining Values § Minimum remaining values (MRV): § Choose the variable with the fewest legal values § Why min rather than max? § Called most constrained variable § “Fail-fast” ordering

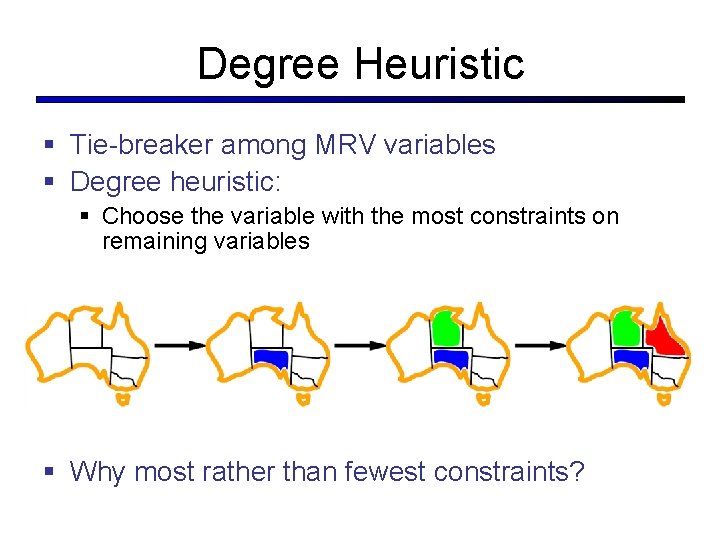
Degree Heuristic § Tie-breaker among MRV variables § Degree heuristic: § Choose the variable with the most constraints on remaining variables § Why most rather than fewest constraints?

Least Constraining Value § Given a choice of variable: § Choose the least constraining value § The one that rules out the fewest values in the remaining variables § Note that it may take some computation to determine this! § Why least rather than most? § Combining these heuristics makes 1000 queens feasible

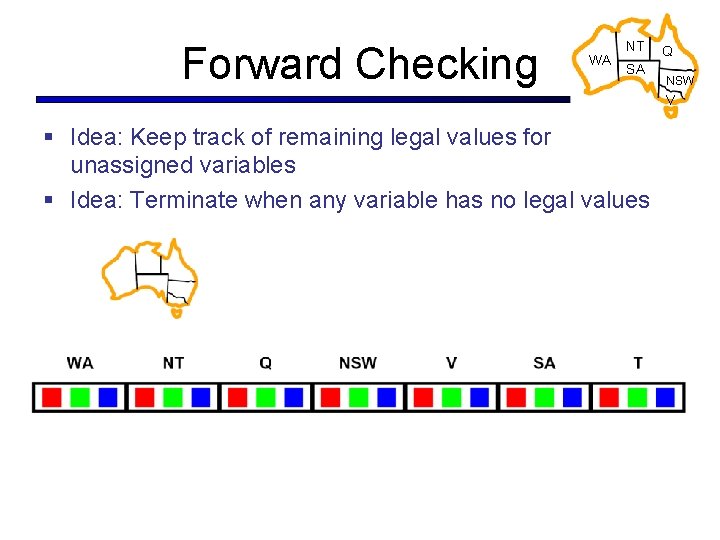
Forward Checking WA NT SA Q NSW V § Idea: Keep track of remaining legal values for unassigned variables § Idea: Terminate when any variable has no legal values

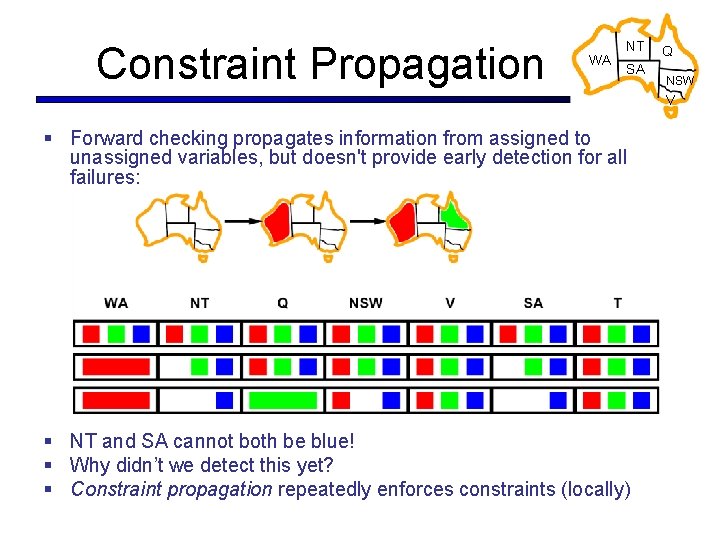
Constraint Propagation WA NT SA Q NSW V § Forward checking propagates information from assigned to unassigned variables, but doesn't provide early detection for all failures: § NT and SA cannot both be blue! § Why didn’t we detect this yet? § Constraint propagation repeatedly enforces constraints (locally)

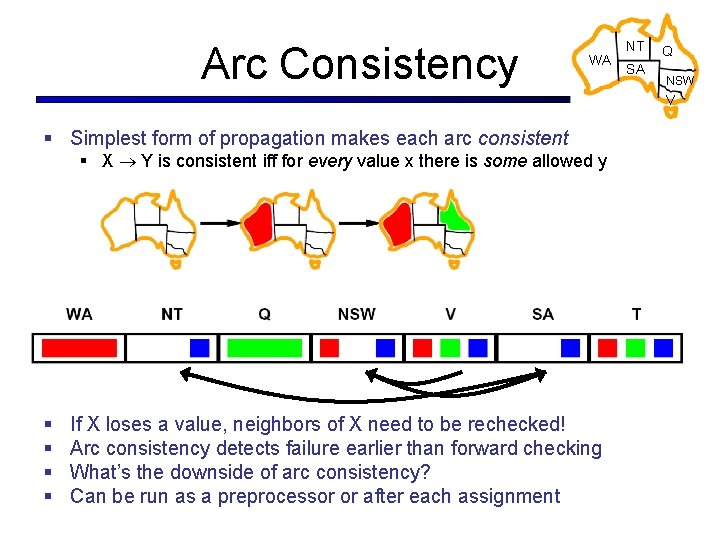
Arc Consistency WA NT SA Q NSW V § Simplest form of propagation makes each arc consistent § X Y is consistent iff for every value x there is some allowed y § § If X loses a value, neighbors of X need to be rechecked! Arc consistency detects failure earlier than forward checking What’s the downside of arc consistency? Can be run as a preprocessor or after each assignment

Conversion to CNF B 1, 1 (P 1, 2 P 2, 1) 1. Eliminate , replacing α β with (α β) (β α). (B 1, 1 (P 1, 2 P 2, 1)) ((P 1, 2 P 2, 1) B 1, 1) 2. Eliminate , replacing α β with α β. ( B 1, 1 P 1, 2 P 2, 1) ( (P 1, 2 P 2, 1) B 1, 1) 3. Move inwards using de Morgan's rules and doublenegation: ( B 1, 1 P 1, 2 P 2, 1) (( P 1, 2 P 2, 1) B 1, 1) 4. Apply distributivity law ( over ) and flatten: ( B 1, 1 P 1, 2 P 2, 1) ( P 1, 2 B 1, 1) ( P 2, 1 B 1, 1)

Resolution Conjunctive Normal Form (CNF) conjunction of disjunctions of literals E. g. , (A B) (B C D) : Basic intuition, resolve B, B to get (A) ( C D) (why? ) § Resolution inference rule (for CNF): li … lk, m 1 … mn l 1 … li-1 li+1 … lk m 1 … mj-1 mj+1 . . . mn where li and mj are complementary literals. E. g. , P 1, 3 P 2, 2, P 2, 2 P 1, 3 § Resolution is sound and complete for propositional logic. § Basic Use: KB ╞ α iff (KB α) is unsatisfiable

Some examples of FOL sentences § How expressive is FOL? § Some examples from natural language § Every gardener likes the sun. § x gardener(x) => likes (x, Sun) § You can fool some of the people all of the time § x (person(x) ^ ( t) (time(t) => can-fool(x, t))) § You can fool all of the people some of the time. § x (person(x) => ( t) (time(t) ^ can-fool(x, t))) § No purple mushroom is poisonous. § ~ x purple(x) ^ mushroom(x) ^ poisonous(x) § or, equivalently, x (mushroom(x) ^ purple(x)) => ~poisonous(x)