CS 184 a Computer Architecture Structure and Organization

CS 184 a: Computer Architecture (Structure and Organization) Day 16: February 14, 2003 Interconnect 6: Mo. T Caltech CS 184 Winter 2003 -- De. Hon 1

Previously • HSRA/BFT – natural hierarchical network – Switches scale O(N) • Mesh – natural 2 D network – Switches scale W(Np+0. 5) Caltech CS 184 Winter 2003 -- De. Hon 2

Today • • Good Mesh properties HSRA vs. Mesh Mo. T Grand unified network theory – Mo. T vs. HSRA – Mo. T vs. Mesh Caltech CS 184 Winter 2003 -- De. Hon 3

Mesh 1. Wire delay can be Manhattan Distance 2. Network provides Manhattan Distance route from source to sink Caltech CS 184 Winter 2003 -- De. Hon 4

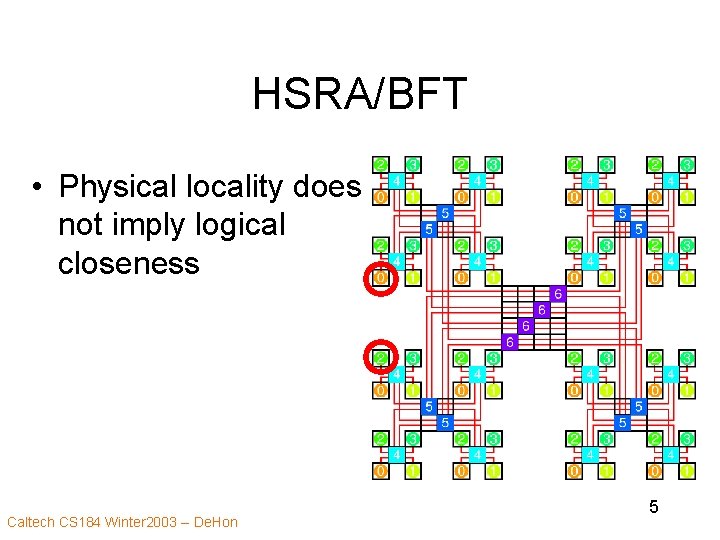
HSRA/BFT • Physical locality does not imply logical closeness Caltech CS 184 Winter 2003 -- De. Hon 5

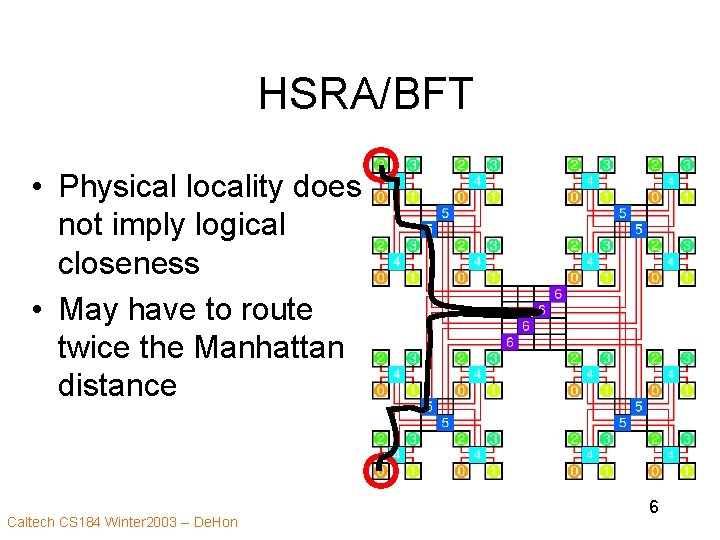
HSRA/BFT • Physical locality does not imply logical closeness • May have to route twice the Manhattan distance Caltech CS 184 Winter 2003 -- De. Hon 6

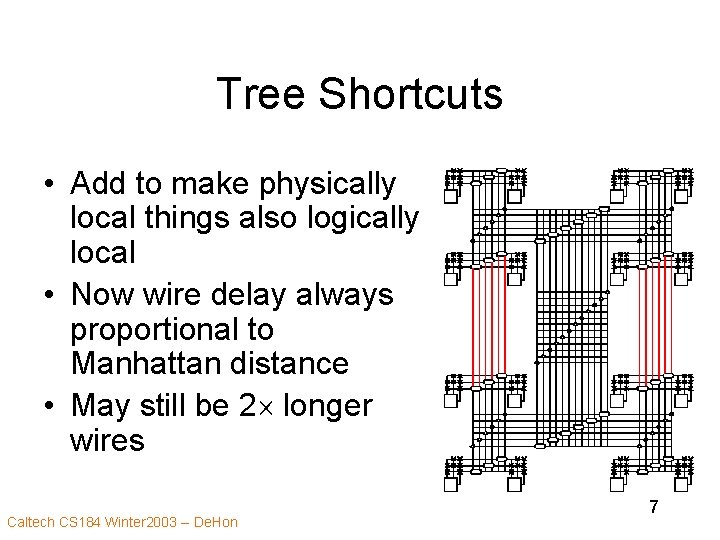
Tree Shortcuts • Add to make physically local things also logically local • Now wire delay always proportional to Manhattan distance • May still be 2 longer wires Caltech CS 184 Winter 2003 -- De. Hon 7

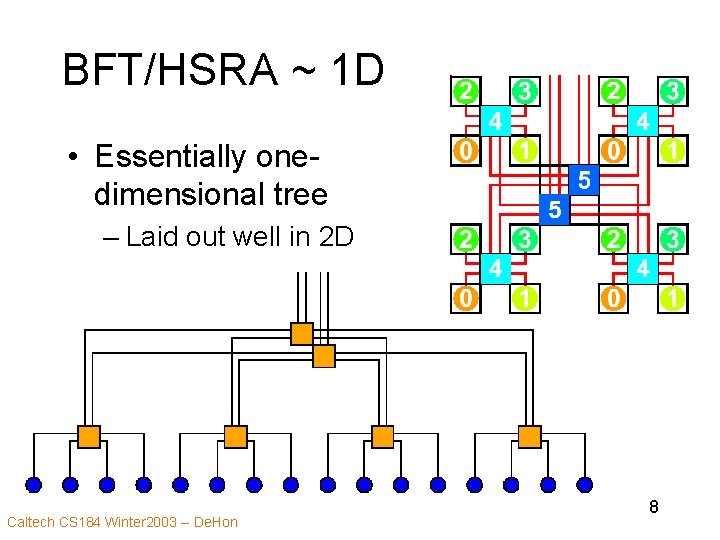
BFT/HSRA ~ 1 D • Essentially onedimensional tree – Laid out well in 2 D Caltech CS 184 Winter 2003 -- De. Hon 8

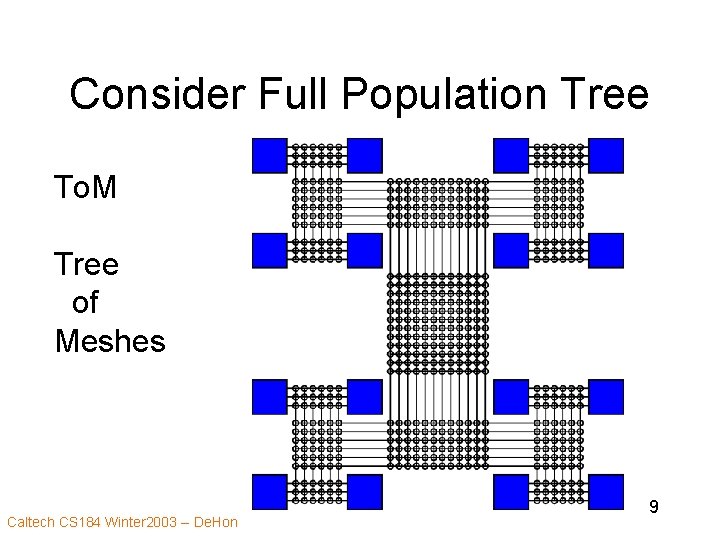
Consider Full Population Tree To. M Tree of Meshes Caltech CS 184 Winter 2003 -- De. Hon 9

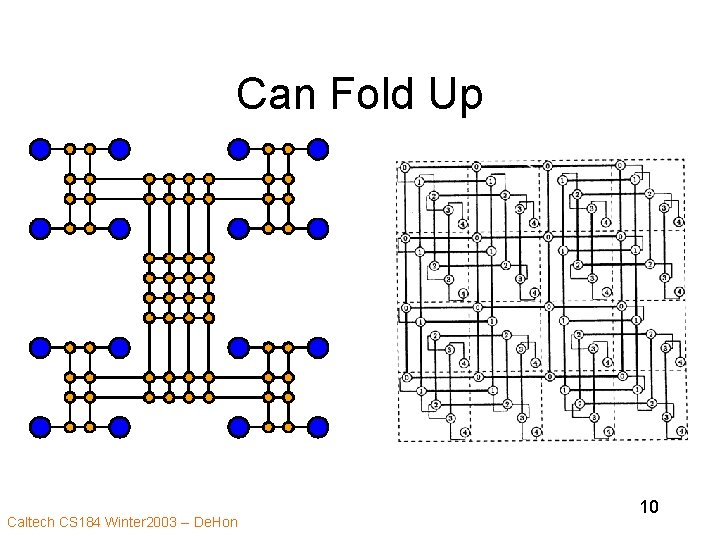
Can Fold Up Caltech CS 184 Winter 2003 -- De. Hon 10

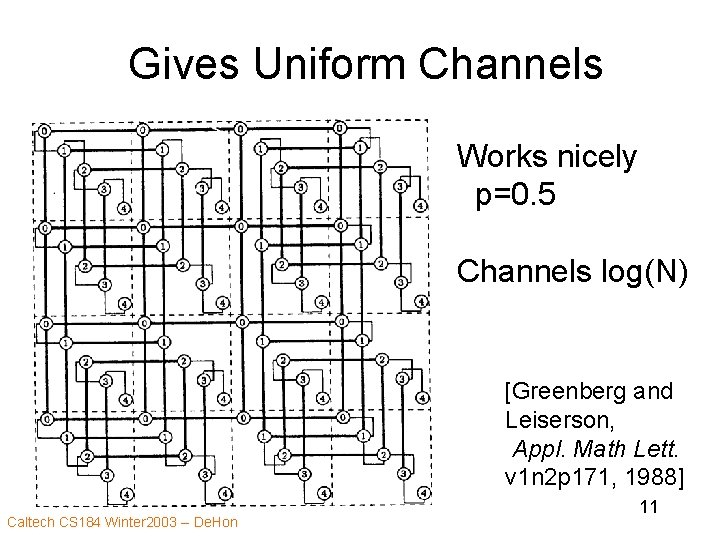
Gives Uniform Channels Works nicely p=0. 5 Channels log(N) [Greenberg and Leiserson, Appl. Math Lett. v 1 n 2 p 171, 1988] Caltech CS 184 Winter 2003 -- De. Hon 11

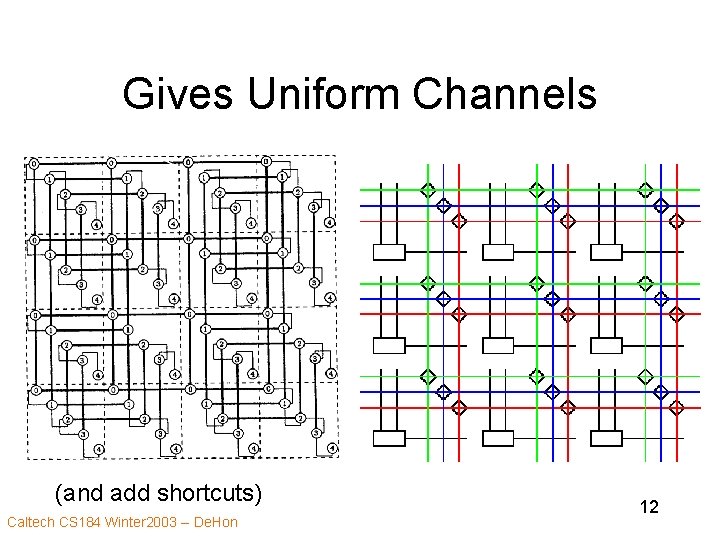
Gives Uniform Channels (and add shortcuts) Caltech CS 184 Winter 2003 -- De. Hon 12

How wide are channels? Caltech CS 184 Winter 2003 -- De. Hon 13

How wide are channels? Caltech CS 184 Winter 2003 -- De. Hon 14

How wide are channels? • A constant factor wider than lower bound! • P=2/3 ~8 • P=3/4 ~5. 5 Caltech CS 184 Winter 2003 -- De. Hon 15

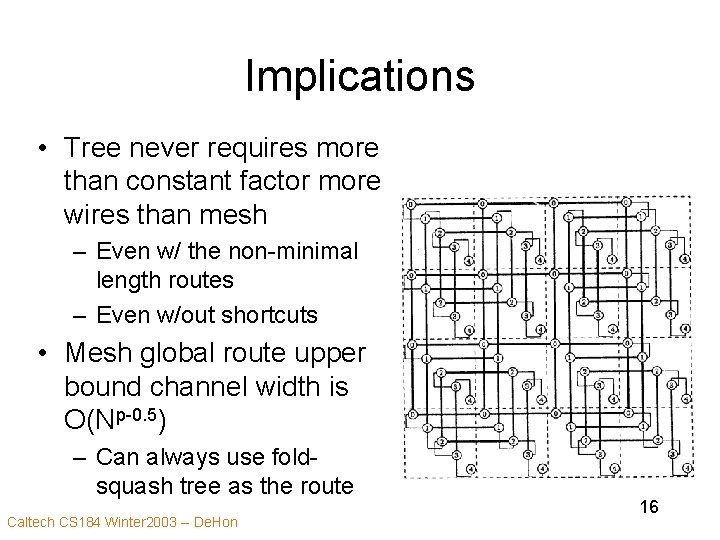
Implications • Tree never requires more than constant factor more wires than mesh – Even w/ the non-minimal length routes – Even w/out shortcuts • Mesh global route upper bound channel width is O(Np-0. 5) – Can always use foldsquash tree as the route Caltech CS 184 Winter 2003 -- De. Hon 16

Mo. T Caltech CS 184 Winter 2003 -- De. Hon 17

Recall: Mesh Switches • Switches per switchbox: – 6 w/Lseg • Switches into network: – (K+1) w • Switches per PE: – 6 w/Lseg + Fc (K+1) w – w = c. Np-0. 5 – Total Np-0. 5 • Total Switches: N*(Sw/PE) Np+0. 5 > N Caltech CS 184 Winter 2003 -- De. Hon 18

Recall: Mesh Switches • Switches per PE: – 6 w/Lseg + Fc (K+1) w – w = c. Np-0. 5 – Total Np-0. 5 • Not change for – Any constant Fc – Any constant Lseg Caltech CS 184 Winter 2003 -- De. Hon 19

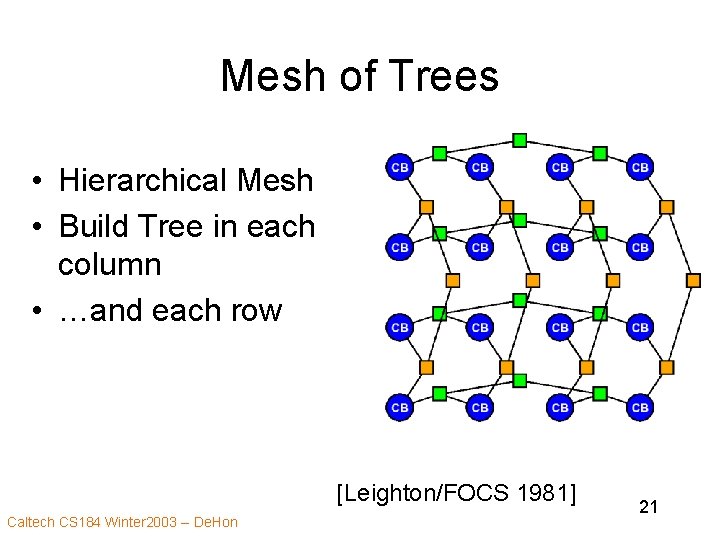
Mesh of Trees • Hierarchical Mesh • Build Tree in each column [Leighton/FOCS 1981] Caltech CS 184 Winter 2003 -- De. Hon 20

Mesh of Trees • Hierarchical Mesh • Build Tree in each column • …and each row [Leighton/FOCS 1981] Caltech CS 184 Winter 2003 -- De. Hon 21

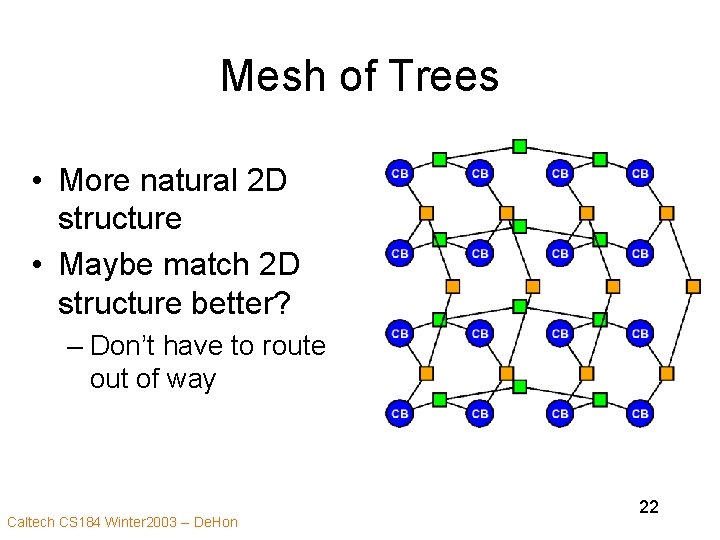
Mesh of Trees • More natural 2 D structure • Maybe match 2 D structure better? – Don’t have to route out of way Caltech CS 184 Winter 2003 -- De. Hon 22

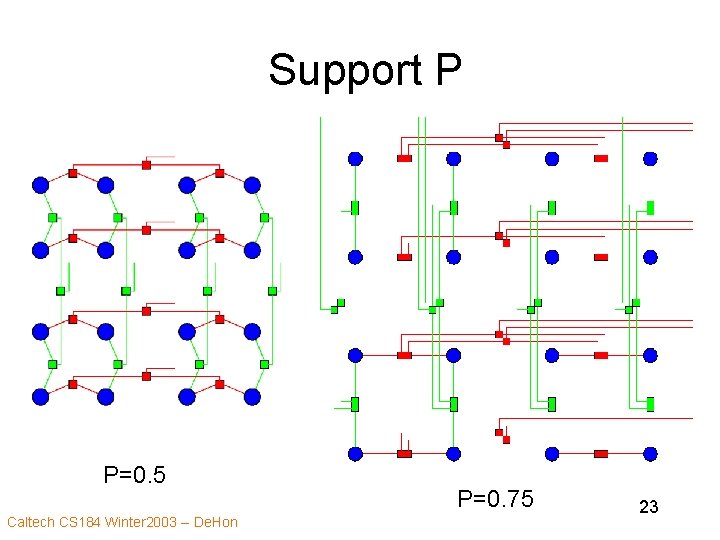
Support P P=0. 5 Caltech CS 184 Winter 2003 -- De. Hon P=0. 75 23

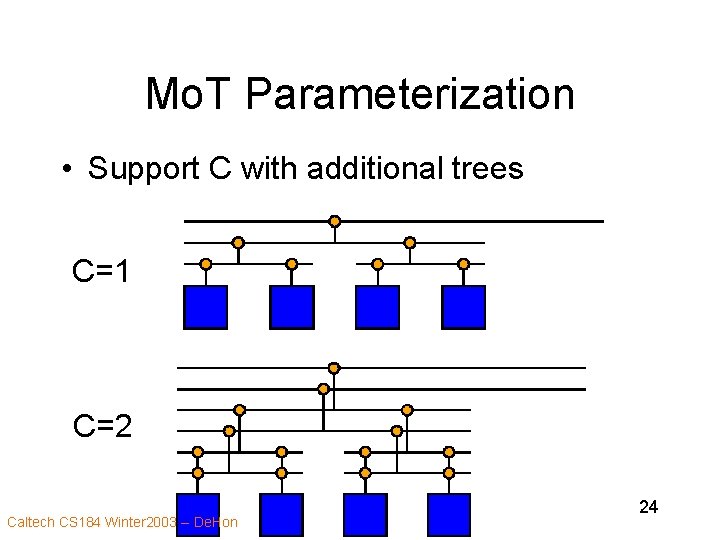
Mo. T Parameterization • Support C with additional trees C=1 C=2 Caltech CS 184 Winter 2003 -- De. Hon 24

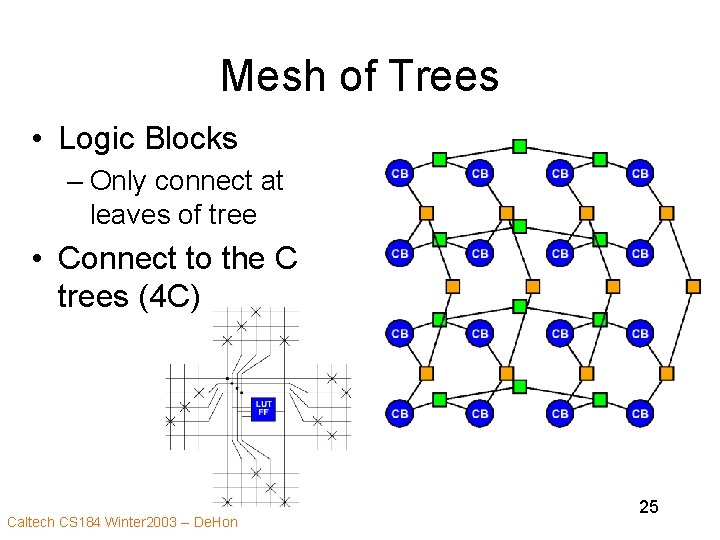
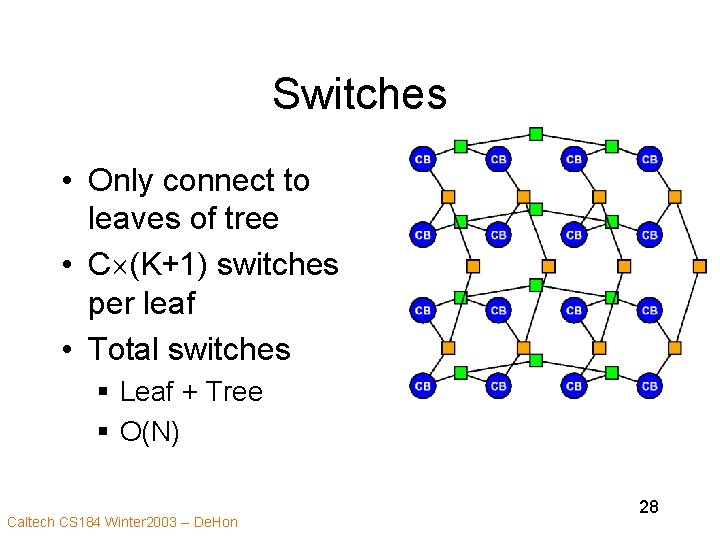
Mesh of Trees • Logic Blocks – Only connect at leaves of tree • Connect to the C trees (4 C) Caltech CS 184 Winter 2003 -- De. Hon 25

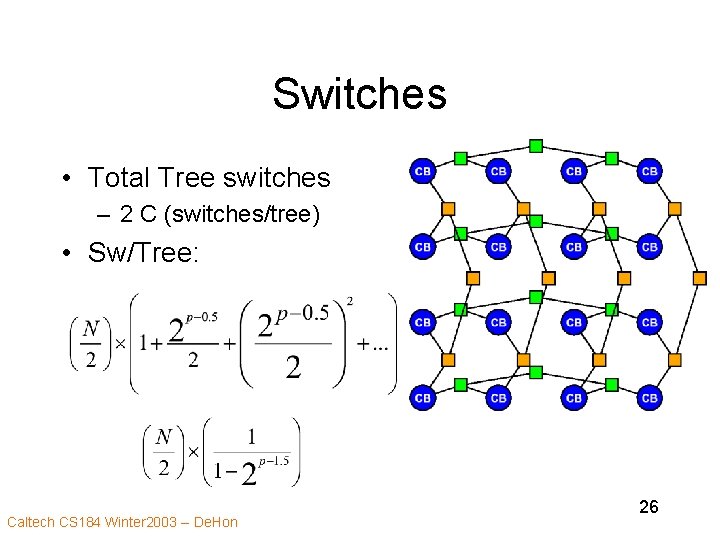
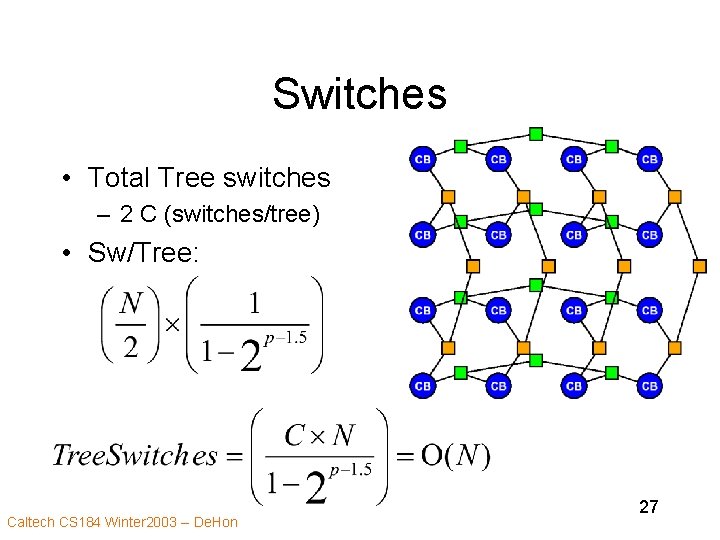
Switches • Total Tree switches – 2 C (switches/tree) • Sw/Tree: Caltech CS 184 Winter 2003 -- De. Hon 26

Switches • Total Tree switches – 2 C (switches/tree) • Sw/Tree: Caltech CS 184 Winter 2003 -- De. Hon 27

Switches • Only connect to leaves of tree • C (K+1) switches per leaf • Total switches § Leaf + Tree § O(N) Caltech CS 184 Winter 2003 -- De. Hon 28

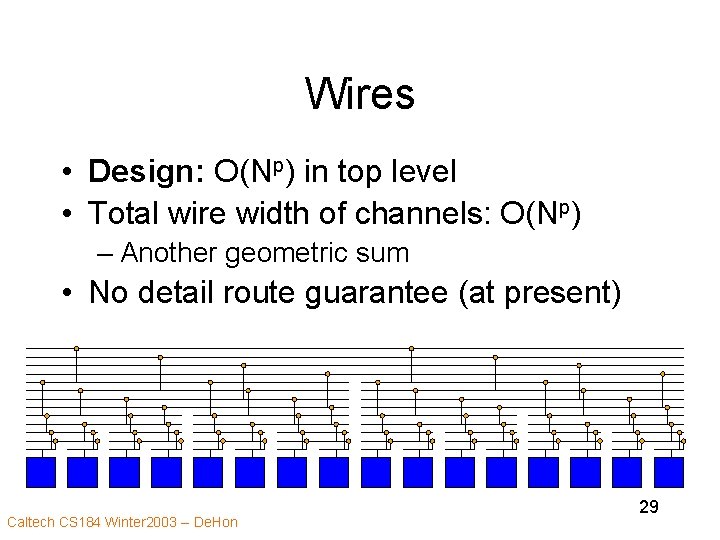
Wires • Design: O(Np) in top level • Total wire width of channels: O(Np) – Another geometric sum • No detail route guarantee (at present) Caltech CS 184 Winter 2003 -- De. Hon 29

Empirical Results • Benchmark: Toronto 20 • Compare to Lseg=1, Lseg=4 – CLMA ~ 8 K LUTs • Mesh(Lseg=4): w=14 122 switches • Mo. T(p=0. 67): C=4 89 switches – Benchmark wide: 10% less • CLMA largest • Asymptotic advantage Caltech CS 184 Winter 2003 -- De. Hon 30

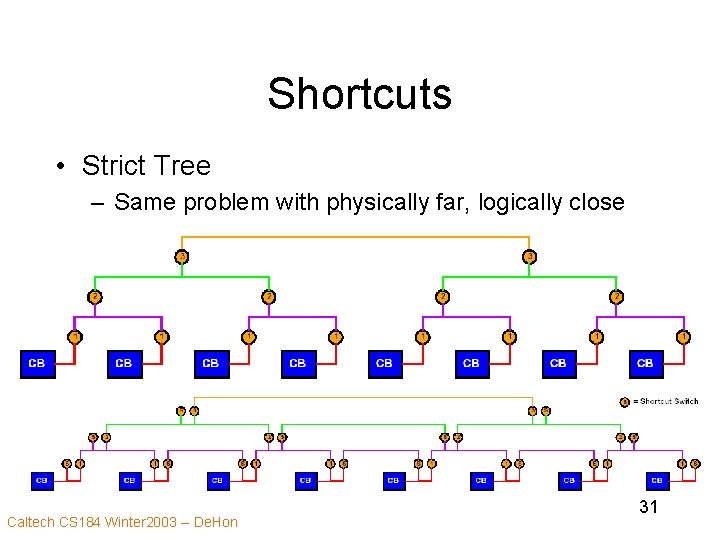
Shortcuts • Strict Tree – Same problem with physically far, logically close Caltech CS 184 Winter 2003 -- De. Hon 31

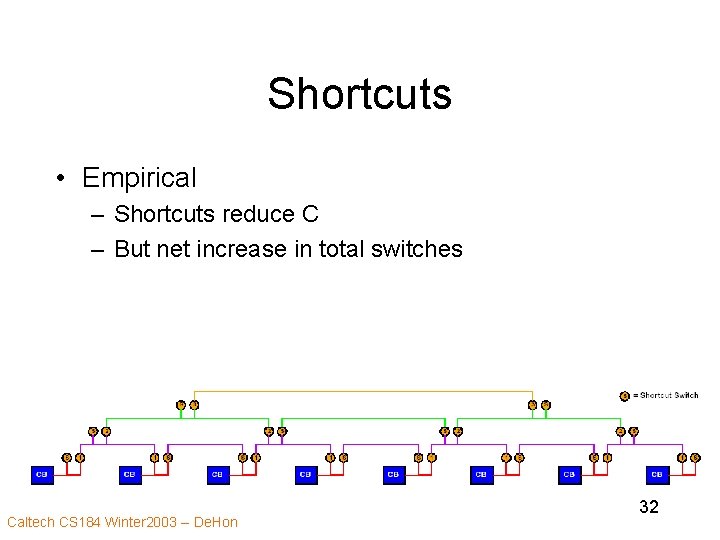
Shortcuts • Empirical – Shortcuts reduce C – But net increase in total switches Caltech CS 184 Winter 2003 -- De. Hon 32

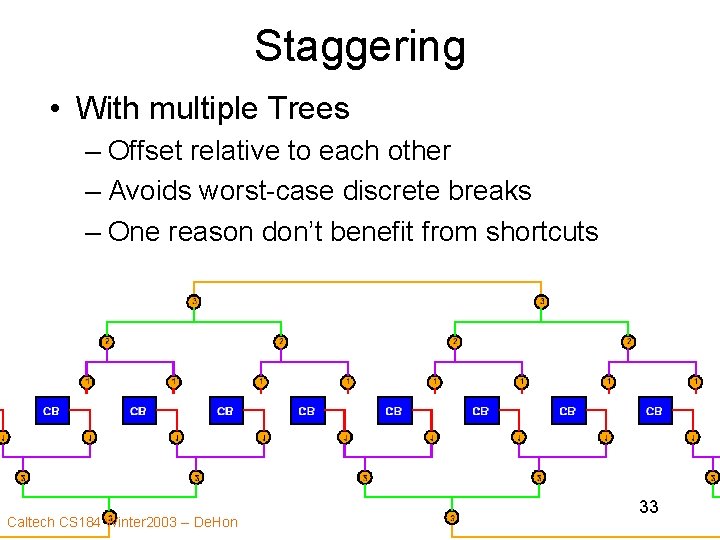
Staggering • With multiple Trees – Offset relative to each other – Avoids worst-case discrete breaks – One reason don’t benefit from shortcuts Caltech CS 184 Winter 2003 -- De. Hon 33

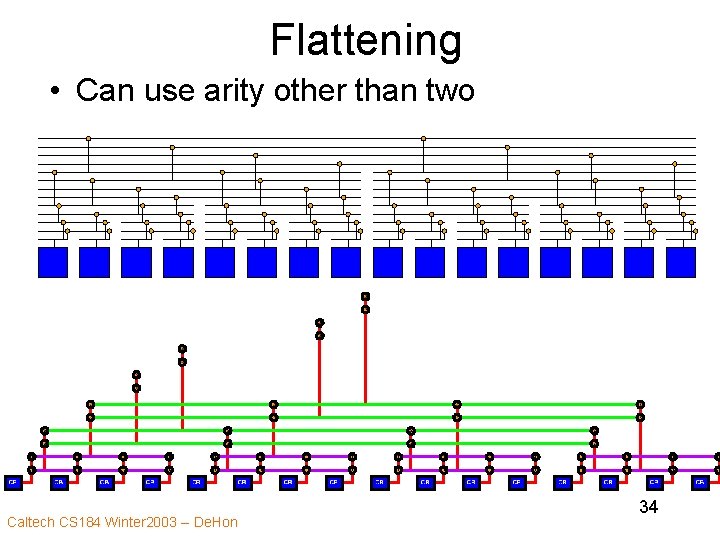
Flattening • Can use arity other than two Caltech CS 184 Winter 2003 -- De. Hon 34

Mo. T Parameters • • • Shortcuts Staggering Corner Turns Arity Flattening Caltech CS 184 Winter 2003 -- De. Hon 35

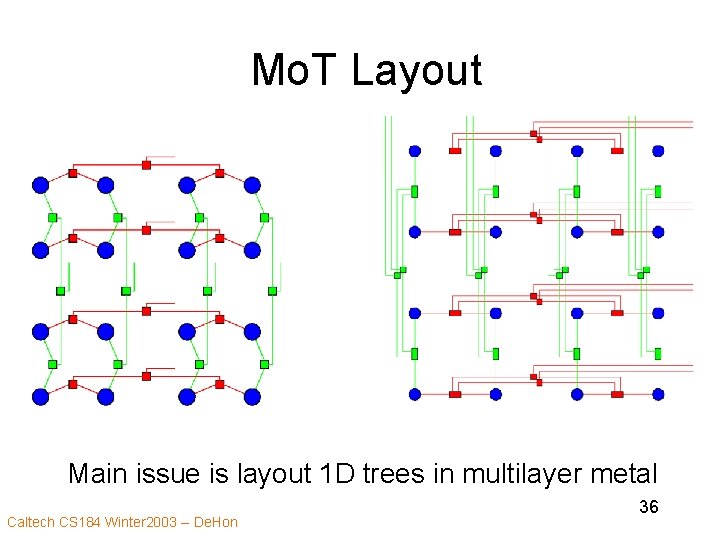
Mo. T Layout Main issue is layout 1 D trees in multilayer metal Caltech CS 184 Winter 2003 -- De. Hon 36

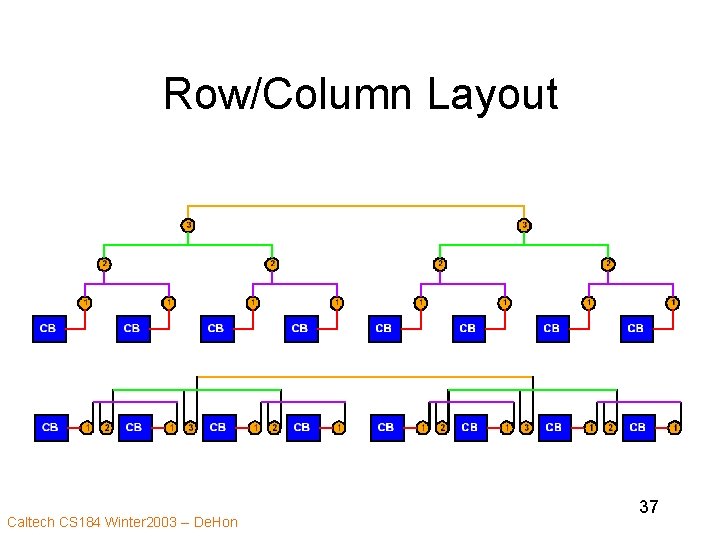
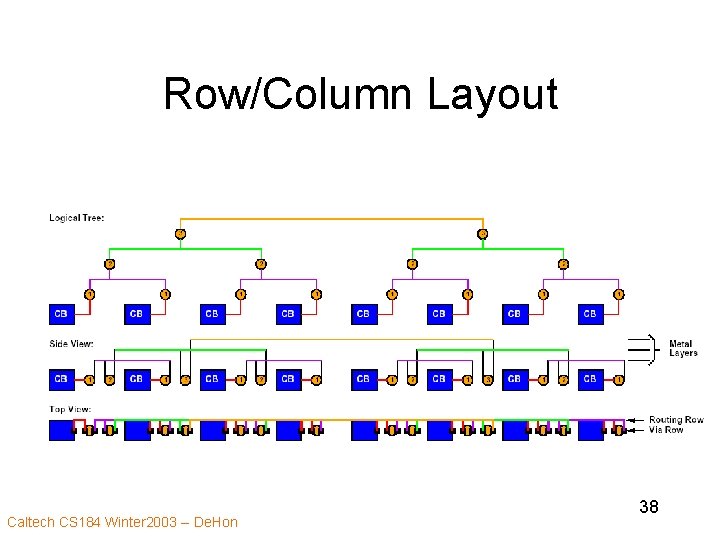
Row/Column Layout Caltech CS 184 Winter 2003 -- De. Hon 37

Row/Column Layout Caltech CS 184 Winter 2003 -- De. Hon 38

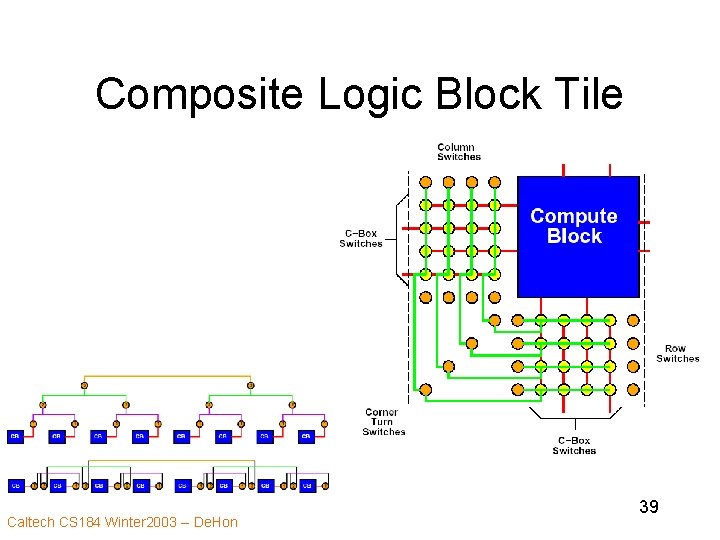
Composite Logic Block Tile Caltech CS 184 Winter 2003 -- De. Hon 39

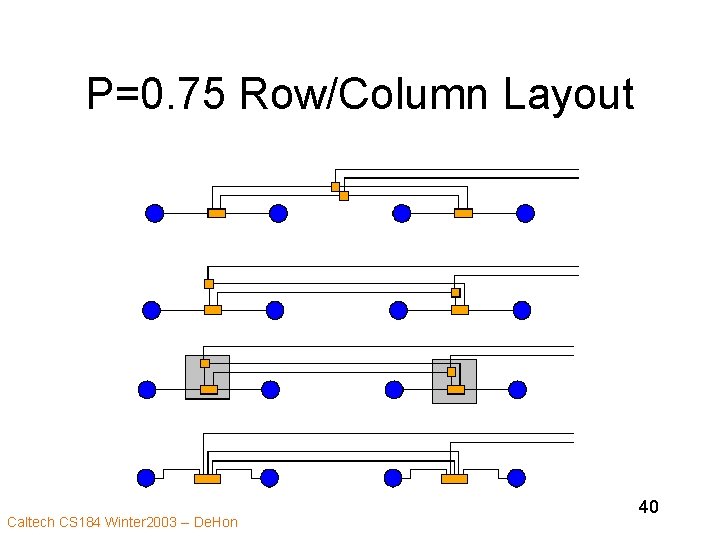
P=0. 75 Row/Column Layout Caltech CS 184 Winter 2003 -- De. Hon 40

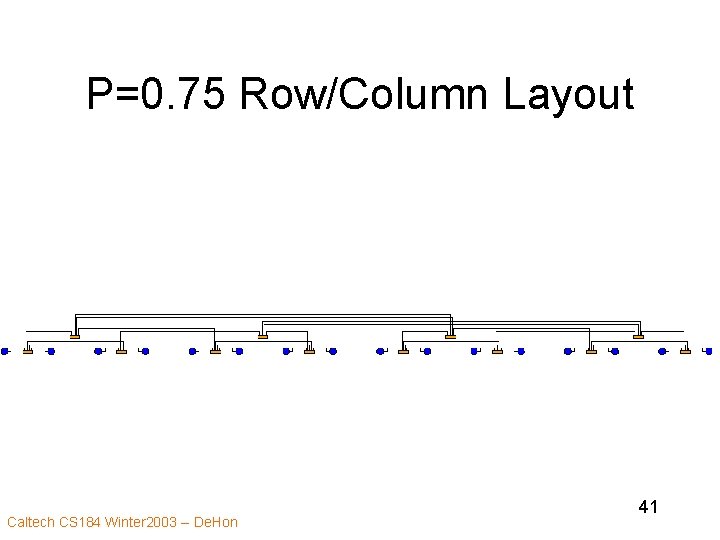
P=0. 75 Row/Column Layout Caltech CS 184 Winter 2003 -- De. Hon 41

Mo. T Layout • Easily laid out in Multiple metal layers – Minimal O(Np-0. 5) layers • Contain constant switching area per LB – Even with p>0. 5 Caltech CS 184 Winter 2003 -- De. Hon 42

Relation? Caltech CS 184 Winter 2003 -- De. Hon 43

How Related? • What lessons translate amongst networks? • Once understand design space – Get closer together • Ideally – One big network design we can parameterize Caltech CS 184 Winter 2003 -- De. Hon 44

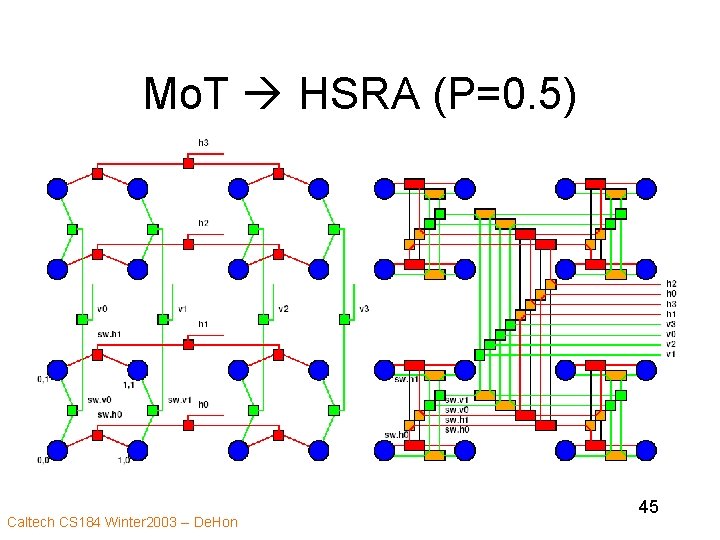
Mo. T HSRA (P=0. 5) Caltech CS 184 Winter 2003 -- De. Hon 45

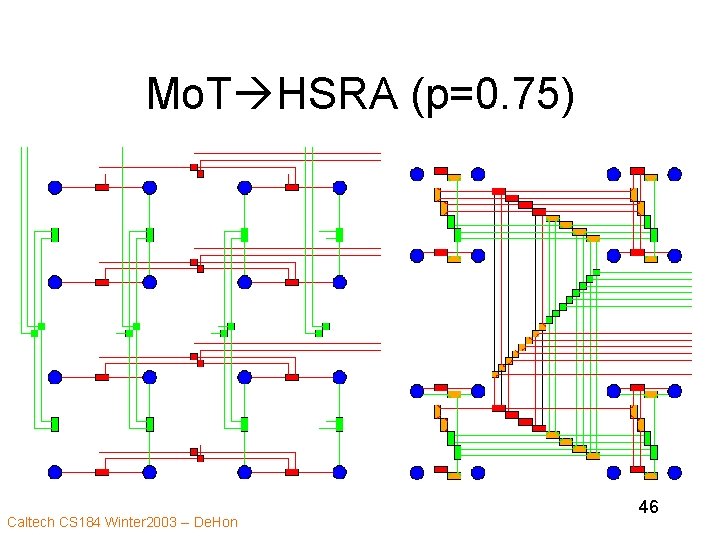
Mo. T HSRA (p=0. 75) Caltech CS 184 Winter 2003 -- De. Hon 46

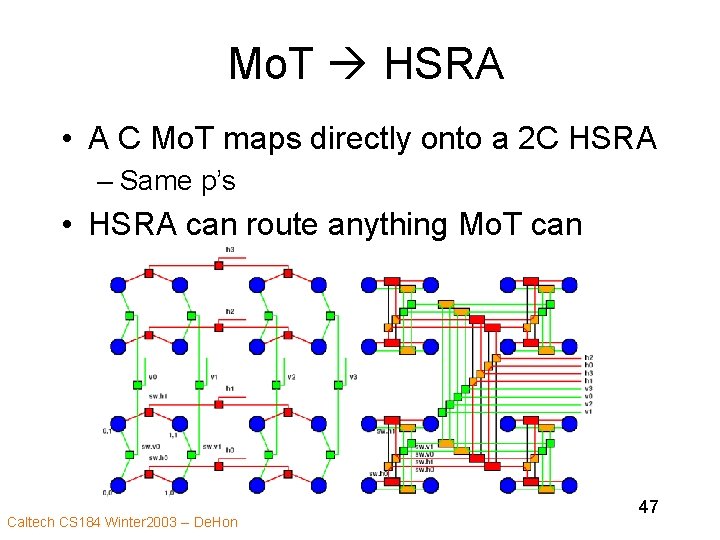
Mo. T HSRA • A C Mo. T maps directly onto a 2 C HSRA – Same p’s • HSRA can route anything Mo. T can Caltech CS 184 Winter 2003 -- De. Hon 47

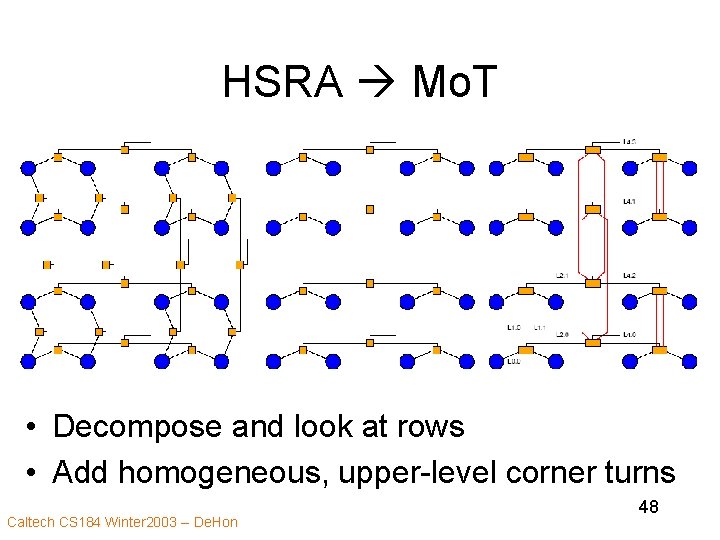
HSRA Mo. T • Decompose and look at rows • Add homogeneous, upper-level corner turns Caltech CS 184 Winter 2003 -- De. Hon 48

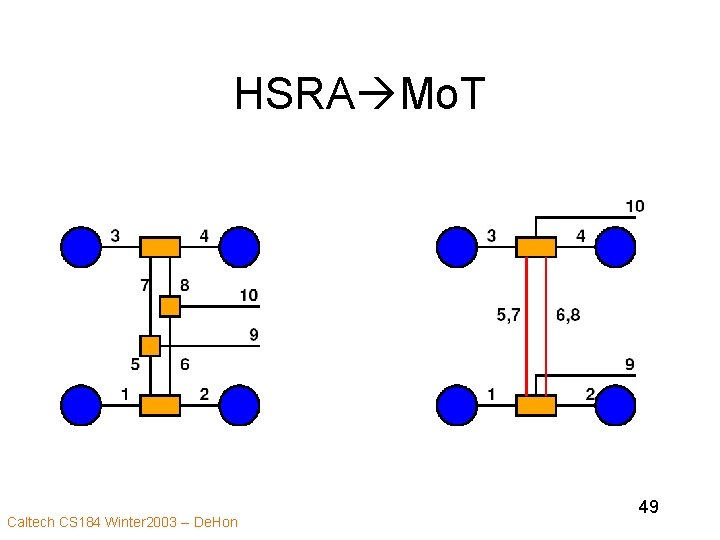
HSRA Mo. T Caltech CS 184 Winter 2003 -- De. Hon 49

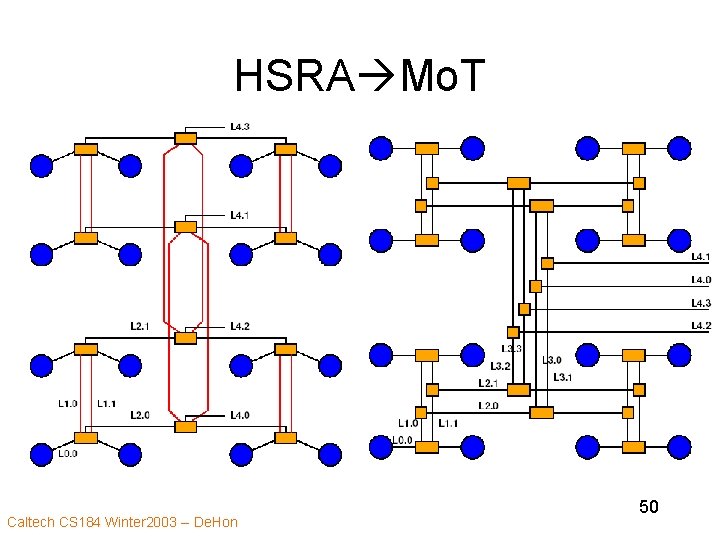
HSRA Mo. T Caltech CS 184 Winter 2003 -- De. Hon 50

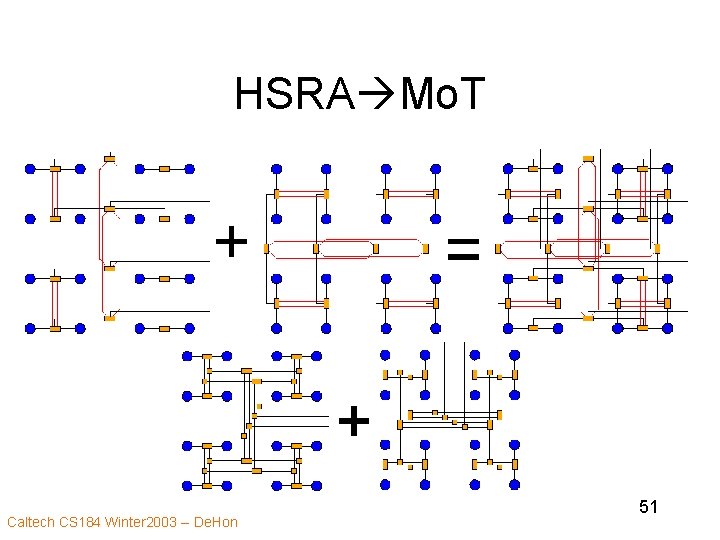
HSRA Mo. T Caltech CS 184 Winter 2003 -- De. Hon 51

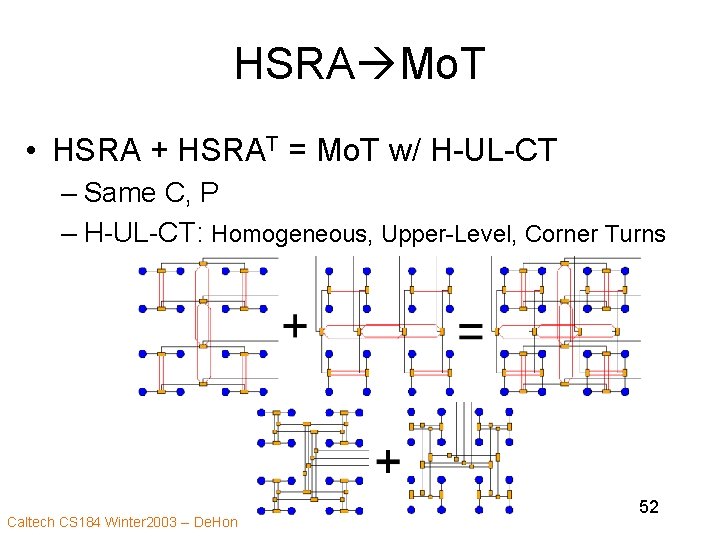
HSRA Mo. T • HSRA + HSRAT = Mo. T w/ H-UL-CT – Same C, P – H-UL-CT: Homogeneous, Upper-Level, Corner Turns Caltech CS 184 Winter 2003 -- De. Hon 52

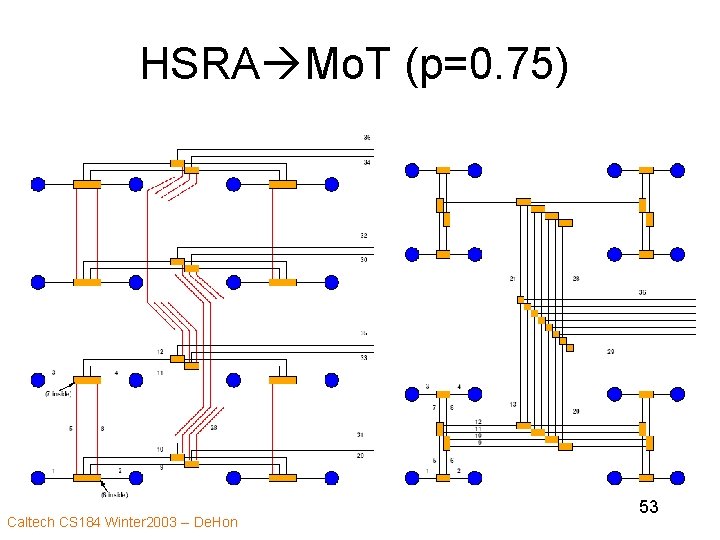
HSRA Mo. T (p=0. 75) Caltech CS 184 Winter 2003 -- De. Hon 53

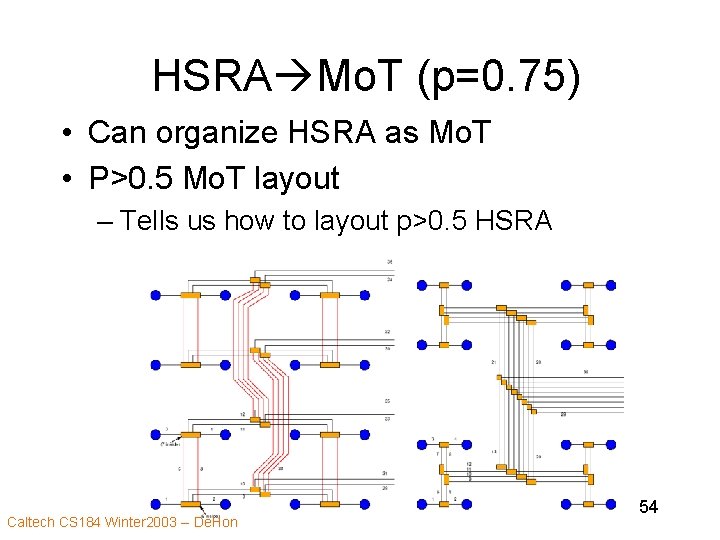
HSRA Mo. T (p=0. 75) • Can organize HSRA as Mo. T • P>0. 5 Mo. T layout – Tells us how to layout p>0. 5 HSRA Caltech CS 184 Winter 2003 -- De. Hon 54

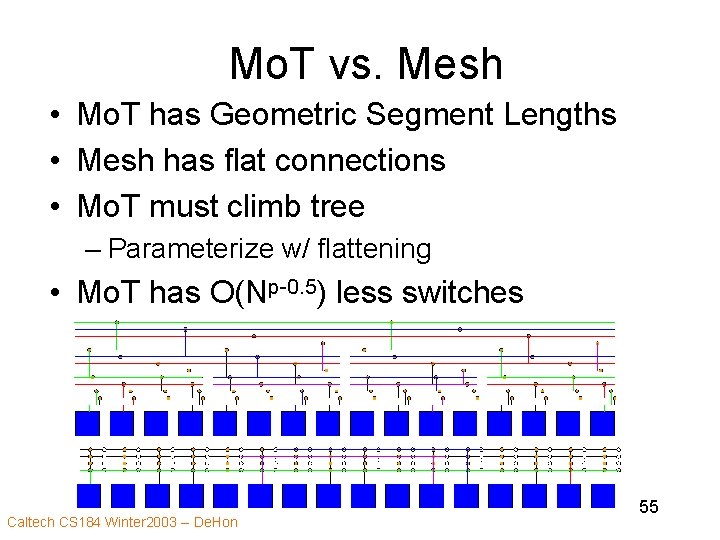
Mo. T vs. Mesh • Mo. T has Geometric Segment Lengths • Mesh has flat connections • Mo. T must climb tree – Parameterize w/ flattening • Mo. T has O(Np-0. 5) less switches Caltech CS 184 Winter 2003 -- De. Hon 55

Mo. T vs. Mesh • Wires – Asymptotically the same (p>0. 5) – Cases where Mesh requires constant less – Cases where require same number Caltech CS 184 Winter 2003 -- De. Hon 56

Admin • Monday = President’s Day Holiday – No Class – (CS Systems down for Maintenance) – Assignment due Wed. as a result Caltech CS 184 Winter 2003 -- De. Hon 57

Big Ideas • Networks driven by same wiring requirements – Have similar wiring asymptotes • Can bound – Network differences – Worst-case mesh global routing • Hierarchy structure allows to save switches – O(N) vs. W(Np+0. 5) Caltech CS 184 Winter 2003 -- De. Hon 58