CS 1813 Discrete Mathematics Review of Predicate Calculus

CS 1813 – Discrete Mathematics Review of Predicate Calculus Set Theory Inductive Definition Proof by Mathematical Induction 1

What is a Predicate? q Predicate § Parameterized collection of propositions § P(x) ü Typically a different proposition for each x ü Universe of discourse – Values that x may take q Universe of discourse § Must be specified ü Otherwise, all bets off — muchas contradicciónes § Non-empty ü Empty universe calls for special handling ü Default assumption: non-empty universe CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 2

— the Universal Quantifier, Forall q x. P(x) § This formula is a WFF of predicate calculus whenever P(x) is a WFF of predicate calculus § True if the proposition P(x) is True for all x’s in the universe of discourse § False if there is some x in the universe of discourse for which P(x) is False § Equivalent to forming the Logical And of all P(x)’s q Example – S predicate about sum § S(n) sum[x 1, x 2, …, xn] = x 1 + x 2 + … + xn § n. S(n) ü Universe of discourse: natural numbers N = {0, 1, 2, … } ü n. S(n) means S(0) S(1) S(2) … ü So, “ ” provides a way to write formulas that would contain an infinite number of symbols if written in propositional calculus notation (but infinitely long formulas aren’t WFFs) CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 3

—the Existential Quantifier, There Exists q x. P(x) § This formula is a WFF of predicate calculus whenever P(x) is a WFF of predicate calculus § True if there is at least one x in the universe of discourse for which the proposition P(x) is True § False if x. P(x) is True § Equivalent to forming the Logical Or of all P(x)’s q Example – E predicate about maximum § E(n, k) maximum[s 1, s 2, …, sn] = sk § k. E(23, k) ü Universe of discourse: U = {1, 2, …, 23} ü k. E(23, k) means E(23, 1) E(23, 2) … E(23, 23) ü Note: When U is finite, quantifiers not required – Clumsy to write big formulas without quantifiers, though – Without quantifiers, reasoning can be more complex, too CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 4

Free Variables and Bound Variables q Variables in WFFs of predicate calculus § Denoted by lower-case letters § Examples of predicate calculus WFFs with variables s leü F(p, q) G(q, r) b ia r ü ( x. F(x)) (G(y) H(y)) va h c ee? ü ( x. F(x, y) G(y)) (H(z) K(x)) i h W e fr ar variables: p, q, r variables: x, y, z q Free variables and bound variables § Let e stand for a WFF of predicate calculus § Bound variable ü x. e x is bound in the formula x. e § Free variables are variables that are not bound CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 5

Arbitrary Variables q A variable is arbitrary in a proof if it does not occur free in any undischarged assumption of that proof q Examples x. F(x) { E} F(x) x arbitrary? Yes G(x, y) { I} y. G(x, y) x arbitrary? No discharged P(x) Q { EL} P(x) x arbitrary? Yes { I} P(x) Q P(x) { I} x. P(x) Q P(x) CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 6

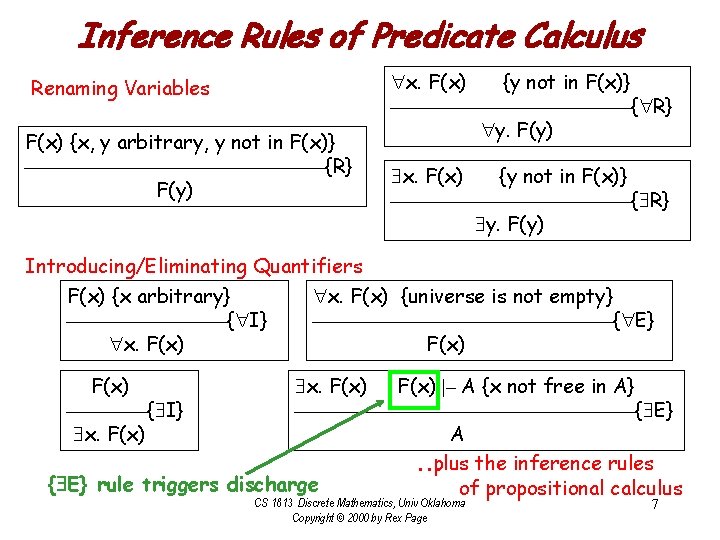
Inference Rules of Predicate Calculus Renaming Variables F(x) {x, y arbitrary, y not in F(x)} {R} F(y) x. F(x) {y not in F(x)} { R} y. F(y) Introducing/Eliminating Quantifiers F(x) {x arbitrary} x. F(x) {universe is not empty} { I} { E} x. F(x) { I} x. F(x) |– A {x not free in A} { E} A. . . plus the inference rules { E} rule triggers discharge of propositional calculus CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 7

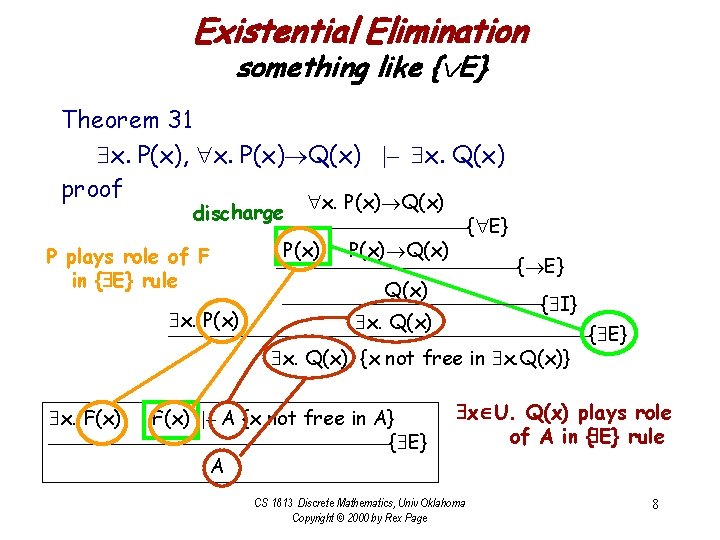
Existential Elimination something like { E} Theorem 31 x. P(x), x. P(x) Q(x) |– x. Q(x) proof x. P(x) Q(x) discharge { E} P(x) Q(x) P plays role of F { E} in { E} rule Q(x) { I} x. P(x) x. Q(x) { E} x. Q(x) {x not free in x. Q(x)} x. F(x) |– A {x not free in A} { E} A x U. Q(x) plays role of A in { E} rule CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 8

Existential Incrimination it’s not legal, really Theorem 9 from Planet X: x. P(x), x. P(x) QED |– x. Q(x) Proof Why not? q Suppose x U, where U is the domain of discourse for x q Is P(x) Q(x) True? § Maybe so, maybe not § “ x. P(x) Q(x)” means P(a) Q(a) is True for at least one value a U § There may be many values b U where P(b) Q(b) is False q Counter-example that disproves theorem § Universe of discourse = {0, 1} § P(0) = True, P(1) = True Note: ( x. P(x)) = True § Q(0) = True, Q(1) = False Note: ( x. P(x) Q(x)) = True § But, ( x. (P(x) Q(x))) is also True ü Because P(1) Q(1) is False § ( x. Q(x)) = False, because Q(1) = False CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 9

Algebraic Laws of Predicate Calculus q n i e t fre ( x. P(x)) ( y. Q(y)) x no ( ( ( ) ) )( ) ) ( x. f(x)) = ( y. f(y)) ( ) ) x ( f n ot i yn CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page { R} 10

Equational Reasoning with Predicates q Theorem ( ( x. P(x)) ( x. Q(x)) ) = ( x. y. P(x) Q(y) ) q Proof of Theorem ( x. P(x)) ( x. Q(x)) = ( ( x. P(x))) ( x. Q(x)) = ( x. P(x)) ( x. Q(x)) = x. ( ( P(x)) ( x. Q(x)) ) = x. ( ( x. Q(x)) ( P(x)) ) = x. ( ( y. Q(y)) ( P(x)) ) = x. y. ( Q(y) ( P(x)) ) = x. y. ( ( P(x)) Q(y) ) = x. y. ( P(x) Q(y) ) {implication} {3. 6} {3. 10} { comm} { R} {3. 10} { comm} {implication} CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page qed 11

Equational Reasoning about Software q Algebraic law of sequence construction x : [x 1, x 2, …, xn] = [x, x 1, x 2, …, xn] -- (: ) (++) : : [a] -> [a] [ ] ++ ys = ys (x : xs) ++ ys = x : (xs ++ ys) -- (++). [] -- (++). : q Algebraic laws of concatenation q An equational argument [x] ++ xs = (x : [ ]) ++ xs = x : ([ ] ++ xs) = x : xs q What did this prove? Theorem (++1) [x] ++ xs = x : xs CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page (: ) (++). : (++). [] ( ) 12

More Software Equations q Algebraic laws of foldr (the big picture) foldr ( ) z [x 1, x 2, …, xn] = x 1 (x 2 … (xn-1 (xn z)) … ) foldr : : (a -> b) -> b -> [a] -> b foldr ( ) z [ ] = z foldr ( ) z (x : xs) = x (foldr ( ) z xs) q The big or -- (foldr). [] -- (foldr). : (/) : : Bool -> Bool -- “little or” – satisfies Boolean laws for or : : [Bool] -> Bool -- “big or” or = foldr (/) False -- (or) q Theorem (or null 1) — or null/first element or ([True] ++ xs) = True or ([True] ++ xs) = or (True : xs) = foldr (/) False (True : xs) = True / (foldr (/) False xs) = True CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page (++1) (or) (foldr). : ( null) 13 qed

The Principle of Mathematical Induction q Universe of discourse: N = {0, 1, 2, …} q Predicate P § P(n) is a proposition whenever n N § Want to prove: n N. P(n) ü That is, to prove that the proposition P(n) is True for all natural numbers n q Principle of Induction § Prove: P(0) § Prove: n N. (P(n) P(n+1)) § Conclude: n N. P(n) principle of induction A way to prove P(n) for all values of n, without proving any P(n) directly except P(0) CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 14

Theorem — or[x, y, …, True, …] = True q Theorem (or T) length ys = n or (ys ++ ([True] ++ xs)) = True q Proof n N. § P(n) length ys = n or (ys ++ ([True] ++ xs)) = True § Base case: P(0) length ys = 0 or(ys ++ ([True] ++ xs)) = True length ys = 0 ys = [ ] zero len theorem or(ys ++ ([True] ++ xs)) = or([ ] ++ ([True] ++ xs)) substitution = or ([True] ++ xs) ++. [] = True or 1 T § Inductive case: P(n) P(n+1) … next slide CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 15

Theorem — or[x, y, …, True, …] = True Inductive Case q Predicate to prove for inductive case § P(n+1) length ys = n+1 or (ys ++ ([True] ++ xs)) = True length ys = n+1 ys [ ] zero len theorem ys = y: zs length zs = n : len corollary or(ys ++ ([True] ++ xs)) = or((y: zs) ++ ([True] ++ xs)) subst length zs = n = or(y: (zs ++ ([True] ++ xs))) length zs = n = y / (or(zs ++ ([True] ++ xs)))) length zs = n = (y / True) length zs = n induction hypothesis (y / True) = True q Conclude: n N. P(n) (++). : (foldr). : P(n) (conj imp) null principle of induction CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page qed 16

Strong Induction n. ( m n. P(m)) P(n) Basic Principle of Induction {Str. Ind} § Prove P(0) is true n. P(n) § Prove P(n+1) is true, n N arbitrary Strong Induction ü Proof of P(n+1) may assume P(n) is true § Conclude n N. P(n) § What if proof of P(n+1) does not make use of P(n)? ü Conclusion n N. P(n) is still valid ü This would be a direct proof using the { I} inference rule ü The principle of induction is a lever that makes the proof easier q Principle of Strong Induction § Prove P(n) for arbitrary n N ü Twist: Can assume k Dn. P(k), where Dn= {k N | k n} § Conclude n N. P(n) Pretty good deal, eh? q Getting Started: D 0 = { } § So, must prove P(0) from scratch (as with old principle of induction) CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 17

msort Termination Proof — inductive case msort (x 1: x 2: xs) = merge (msort ys) (msort zs) where (ys, zs) = deal(x 1: x 2: xs) (msort). : q P(n) (length xs) = n (msort xs) terminates length(msort xs) = n q Proof of P(n) for arbitrary n {2, 3, 4, …} merge terminates (m. T) msort xs = msort(x 1: x 2: ws) (pattern matching) (length xs) 2 = merge (msort ys) (msort zs) (no operation) (msort). : deal terminates (d. S) where (ys, zs) = deal(x 1: x 2: ws) (msort ys) terminates – Why? Ind Hyp implies P(length ys) is True length ys length xs (d. R) strong induction (msort zs) terminates (similar argument) üEach step (matching, deal, msort twice, merge) takes a finite amount of time, so (msort xs) terminates ü length xs = length ys + length zs (d. S) = length(msort ys) + length(msort zs) P(length ys), P(length zs) = length(merge (msort ys) (msort zs)) (m. T) = length(msort xs) (msort). : : – as in above proof CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 18 qed (strong induction)

Haskell Type Specifications q x, y, z : : Integer q xs, ys : : [Integer] q or : : [Bool] -> Bool q (++) : : [e] -> [e] q sum : : Num n => [n] -> n -- x, y, and z have type Integer -- sequences with Integer elements -- function with one argument is sequence with Bool elems delivers value of type Bool -- generic function with two arguments args are sequences with elems of same type is not constrained (can be any type) delivers sequence with elements of same type as those in arguments -- generic function with one argument is a sequence with elems of type n n must a type of class Num is a set of types with +, , … operations q power. Set : : (Eq e, Show e) => Set e -> Set(Set e) -- generic function with one argument is a set with elements of type e delivers set with elements of type (Set e) type e must be both class Eq and class Show Class Eq has == operator, Show displayable CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 19

Inductive Definitions aka Recursive Equations sum : : Num n => [n] -> n sum(x: xs) = x + sum xs sum[ ] = 0 Theorem: sum = foldr (+) 0 length : : [a] -> Int length(x: xs) = 1 + length xs length[ ] = 0 Theorem: length = foldr one. More 0 where one. More x n = 1 + n (sum). : (sum). [] (length). : (length). [] (++) : : [a] -> [a] (x: xs) ++ ys = x: (xs ++ ys) [ ] ++ ys = ys Theorem: xs ++ ys = foldr (: ) ys xs (++). : (++). [] concat : : [[a]] -> [a] concat(xs: xss) = xs ++ concat xss concat[ ] = [ ] Theorem: concat = foldr (++) [ ] (concat). : (concat). [] CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 20

Patterns of Computation Pattern: foldr ( ) z [x 1, x 2, …, xn-1, xn ] = x 1 ( x 2 … (xn-1 ( xn z)) … ) foldr : : (a -> b) -> b -> [a] -> b foldr ( ) z (x: xs) = x foldr ( ) z xs (foldr). : foldr ( ) z [ ] = z (foldr). [] Pattern: map f [x 1, x 2, … xn] = [f x 1, f x 2, … f xn] map : : (a -> b) -> [a] -> [b] map f (x : xs) = (f x) : map f xs map f [ ] = [ ] (map). : (map). [] Pattern: zip. With b [x 1, x 2, … xn] [y 1, y 2, … yn] = [b x 1 y 1, b x 2 y 2, … b xn yn] Note: extra elements in either sequence are dropped zip. With : : (a -> b -> c) -> [a] -> [b] -> [c] zip. With b (x: xs) (y: ys) = (b x y): (zip. With b xs ys) (zip. W). : zip. With b [ ] ys = [ ] (zip. W). []-1 zip. With b xs [ ] = [ ] (zip. W). []-2 CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 21

q {2, 3, 5, 7, 11} q 2 {2, 3, 5, 7, 11} Sets — explicit enumeration — stylized epsilon means “element of” q ={} q {x | p x} q — stylized Greek letter phi denotes empty set — set comprehension § Denotes set with elements x, where (p x) is True {f x | p x} — set comprehension § Denotes set with elements of form (f x), where (p x) is True A B x. (x A x B) — subset A = B (A B) (B A) — set equality A B = {x | x A x B} — union S = {x | A S. x A} — big union A B = {x | x A x B} — intersection S = {x | A S. x A} — big intersection A – B = {x | x A x B} — set difference q q q q A’ = U – A q P(A) = {S | S A} q A B = {(a, b) | a A b B} — complement (U = universe) — power set — Cartesian product CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 22

End of Lecture 23