CS 151 Digital Design Chapter 2 3b Standard

CS 151 : Digital Design Chapter 2 – 3(b) Standard Forms 1

Standard Forms n It is useful to specify Boolean functions in a form that: q q q n Allows comparison for equality. Has a correspondence to the truth tables. Facilitates Boolean expression simplification. Standard Forms in common usage: q q Sum of Minterms (SOM) Product of Maxterms (POM) CS 151 2

Minterms n n n Minterms are AND terms with every variable present once in either true or complemented form. Given that each binary variable may appear normal (e. g. , x) or complemented (e. g. , x’ ), there are 2 n minterms for n variables. Example: Two variables (X and Y)produce 2 x 2 = 4 combinations: XY XY’ X’Y’ n (both normal) (X normal, Y complemented) (X complemented, Y normal) (both complemented) Thus there are four minterms of two variables. CS 151 3

Maxterms n n n Maxterms are OR terms with every variable in true or complemented form. Given that each binary variable may appear normal (e. g. , x) or complemented (e. g. , x’), there are 2 n maxterms for n variables. Example: Two variables (X and Y) produce 2 x 2 = 4 combinations: X+Y’ X’+Y’ (both normal) (X normal, Y complemented) (X complemented, Y normal) (both complemented) CS 151 4

Minterm and Maxterm Relationship n Review: De. Morgan's Theorem (X. Y)’ = X’ + Y’ and (X + Y)‘ = X ‘. Y’ Two-variable example: m 3=X. Y and M 3 = X’ + Y’ Thus M 3 is the complement of m 3 and vice-versa. n Since De. Morgan's Theorem holds for n variables, the above holds for terms of n variables giving: n Mi = mi and mi = Mi n Thus Mi is the complement of mi. CS 151 5

Observations n n In the function tables: q Each minterm has one and only one 1 present in the 2 n terms (a minimum of 1 s). All other entries are 0. q Each maxterm has one and only one 0 present in the 2 n terms All other entries are 1 (a maximum of 1 s). We can implement any function by "ORing" the minterms corresponding to "1" entries in the function table. These are called the minterms of the function. We can implement any function by "ANDing" the maxterms corresponding to "0" entries in the function table. These are called the maxterms of the function. This gives us two standard forms: q Sum of Minterms (SOM) q Product of Maxterms (POM) for stating any Boolean function. CS 151 6

Minterm Function Example n n F(A, B, C, D, E) = m 2 + m 9 + m 17 + m 23 F(A, B, C, D, E) = CS 151 7

Maxterm Function Example n F(A, B, C, D) = M 3. M 8. M 11. M 14 n F(A, B, C, D) = CS 151 8

Minterm Function Example n F = (X’Y’ Z’+X’YZ’+XY’Z+XYZ) = m 0+m 2+m 5+m 7 F(X, Y, Z) = m(0, 2, 5, 7) m 0 m 1 m 2 m 3 m 4 m 5 m 6 m 7 n F’ = (X’Y’Z+X’YZ+XY’Z’+XYZ’) = m 1+m 3+m 4+m 6 F’(X, Y, Z) = m(1, 3, 4, 6) n Note that the minterms of F’ are those missing from F. What is the complement of F’? ? n CS 151 9

Conversion Between Forms = m 1+m 3+m 4+m 6 = m(1, 3, 4, 6) = m 1+m 3+m 4+m 6 = m 1. m 3. m 4. m 6 = M 1. M 3. M 4. M 6 = (X+Y+Z) F (X, Y, Z) = M(1, 3, 4, 6). F F But, from the previous slide F(X, Y, Z) = m(0, 2, 5, 7) Then, m(0, 2, 5, 7) = M(1, 3, 4, 6) To convert between sum-of-minterms and product-of-maxterms form (or vice-versa) we follow these steps: 1. Find the function complement by swapping terms in the list with terms not in the list. 2. Change from products to sums, or vice versa. CS 151 10

Logic 1 Functions n G (X, Y) = m(0, 1, 2, 3) = 1 (always equal to logic 1) X Y G 0 0 1 1 1 0 1 1 A function that includes all the 2 n minterms is equal to logic 1 CS 151 11

Sum of Minterms n Any Boolean function can be expressed as a Sum of Minterms. q n For the function table, the minterms used are the terms corresponding to the 1's. Example: Express E= Y+XZ as a sum of minterms. E(X, Y, Z) = m(0, 1, 2, 4, 5) CS 151 12

Standard Sum-of-Products (SOP) n A sum of minterms form for n variables can be written down directly from a truth table. q q q n Implementation of this form is a two-level network of gates such that: The first level consists of n-input AND gates, and The second level is a single OR gate (with fewer than 2 n inputs). This form often can be simplified so that the corresponding circuit is simpler. CS 151 13

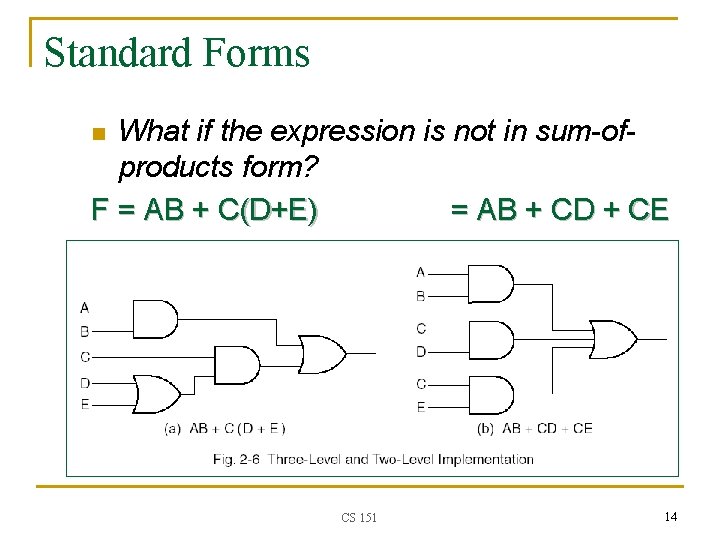
Standard Forms What if the expression is not in sum-ofproducts form? F = AB + C(D+E) = AB + CD + CE n CS 151 14

Standard Sum-of-Products (SOP) n A Simplification Example: n n Writing the minterm expression: F = A B C + ABC Simplifying: F= Simplified F contains 3 literals compared to 15 in minterm F CS 151 15

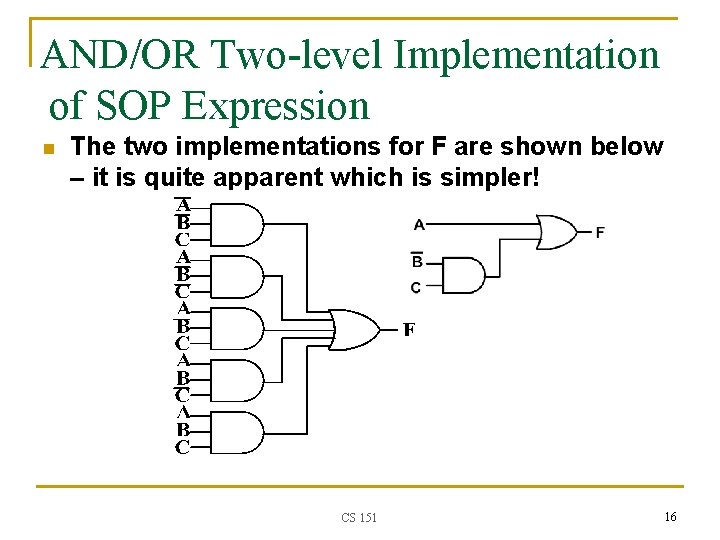
AND/OR Two-level Implementation of SOP Expression n The two implementations for F are shown below – it is quite apparent which is simpler! CS 151 16

Product of Maxterms n Any Boolean Function can be expressed as a Product of Maxterms (POM). q For the function table, the maxterms used are the terms corresponding to the 0's. F = X(Y + Z)(X+Y+Z) CS 151 17

SOP and POS Observations n The previous examples show that: q q q n Standard Forms (Sum-of-minterms, Product-of. Maxterms differ in complexity Boolean algebra can be used to manipulate equations into simpler forms. Simpler equations lead to simpler two-level implementations Questions: q q q How can we attain a “simplest” expression? Is there only one minimum cost circuit? The next part will deal with these issues. CS 151 18