CS 1502 Formal Methods in Computer Science Lecture

Constructing a Truth Table Write down sentence Create the reference columns Until you are

Tautology A sentence S is a tautology if and only if every row of

Logical Possibility A sentence S is logically possible if it could be true (i.

Examples Cube(b) Large(b) Logically possible TW-possible (Tet(c) Cube(c) Dodec(c)) Logically possible Not TW-possible e

Spurious Rows A spurious row in a truth table is a row whose reference

Logical Necessity A sentence S is a logical necessity (logical truth) if and only

Example Not a tautology Logical Necessity TW-Necessity 11

Example Not a tautology Not a Logical Necessity Not a TW-Necessity According to the

Tet(b) Cube(b) Dodec(b) Tet(b) a=a Cube(a) v Cube(b) Cube(a) Small(a) 13

Tautological Equivalence Two sentences S and S’ are tautologically equivalent if and only if

Example S S’ S and S’ are Tautologically Equivalent 15

Logical Equivalence Two sentences S and S’ are logically equivalent if and only if

Example S Not Tautologically equivalent S’ Logically Equivalent 17

Tautological Consequence Sentence Q is a tautological consequence of P 1, P 2, …,

Example premises conclusion Tautological consequence 19

Logical Consequence Sentence Q is a logical consequence of P 1, P 2, …,

premise conclusion Not a tautological consequence Is a logical consequence 21

Summary Necessary Possible Equivalence Consequence S is always true S could be true S

Summary Logical-Consequences of P 1…Pn Tautological. Consequences of P 1…Pn Every tautological consequence of

Summary Every tautological equivalence is a logical equivalence. Not every logical equivalence is a

Summary Every tautology is a logical necessity. Not every logical necessity is a tautology.

Slides: 25

Download presentation

CS 1502 Formal Methods in Computer Science Lecture Notes 4 Tautologies and Logical Truth 1

Constructing a Truth Table Write down sentence Create the reference columns Until you are done: – Pick the next connective to work on – Identify the columns to consider – Fill in truth values in the column EG: ~(A ^ (~A v (B ^ C))) v B (in Boole and on board) 2

Tautology A sentence S is a tautology if and only if every row of its truth table assigns true to S. 3

Example Is (A (B C))) B a tautology? 4

Example 5

Logical Possibility A sentence S is logically possible if it could be true (i. e. , it is true in some world) It is TW-possible if it is true in some world that can be built using the program 6

Examples Cube(b) Large(b) Logically possible TW-possible (Tet(c) Cube(c) Dodec(c)) Logically possible Not TW-possible e e Not Logically possible 7

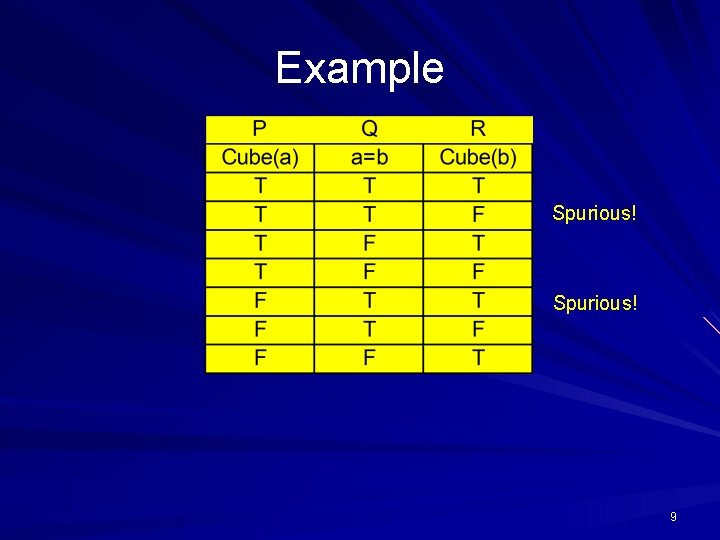
Spurious Rows A spurious row in a truth table is a row whose reference columns describe a situation or circumstance that is impossible to realize on logical grounds. 8

Example Spurious! 9

Logical Necessity A sentence S is a logical necessity (logical truth) if and only if S is true in every logical circumstance. A sentence S is a logical necessity (logical truth) if and only if S is true in every nonspurious row of its truth table. TW-Necessity Logical-Necessity 10

Example Not a tautology Logical Necessity TW-Necessity 11

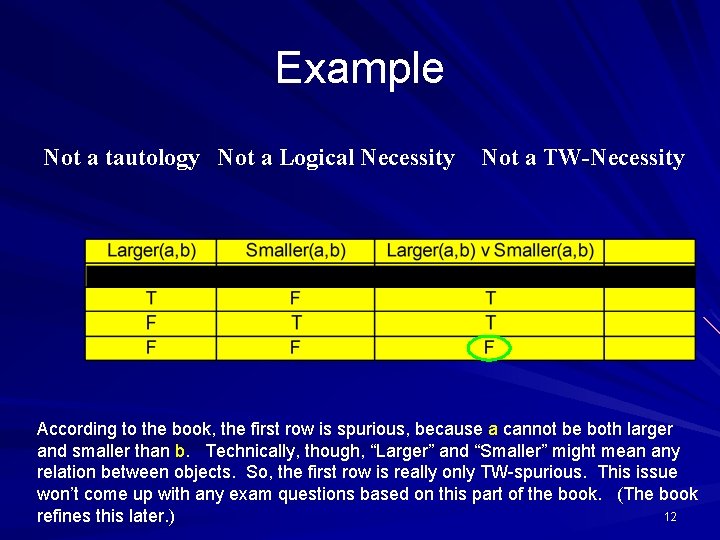
Example Not a tautology Not a Logical Necessity Not a TW-Necessity According to the book, the first row is spurious, because a cannot be both larger and smaller than b. Technically, though, “Larger” and “Smaller” might mean any relation between objects. So, the first row is really only TW-spurious. This issue won’t come up with any exam questions based on this part of the book. (The book 12 refines this later. )

Tet(b) Cube(b) Dodec(b) Tet(b) a=a Cube(a) v Cube(b) Cube(a) Small(a) 13

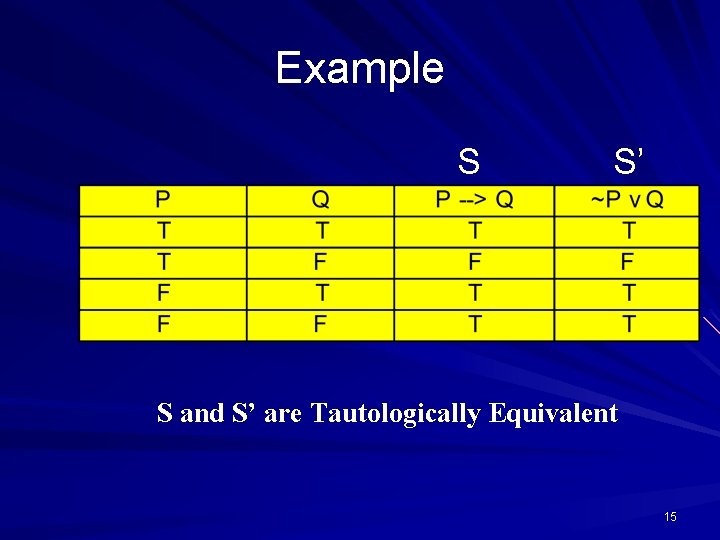
Tautological Equivalence Two sentences S and S’ are tautologically equivalent if and only if every row of their joint truth table assigns the same values to S and S’. 14

Example S S’ S and S’ are Tautologically Equivalent 15

Logical Equivalence Two sentences S and S’ are logically equivalent if and only if every non-spurious row of their joint truth table assigns the same values to S and S’. 16

Example S Not Tautologically equivalent S’ Logically Equivalent 17

Tautological Consequence Sentence Q is a tautological consequence of P 1, P 2, …, Pn if and only if every row that assigns true to all of the premises also assigns true to Q. Remind you of anything? P 1, P 2, …, Pn | Q is also a valid argument! A Con Rule: Tautological Consequence 18

Example premises conclusion Tautological consequence 19

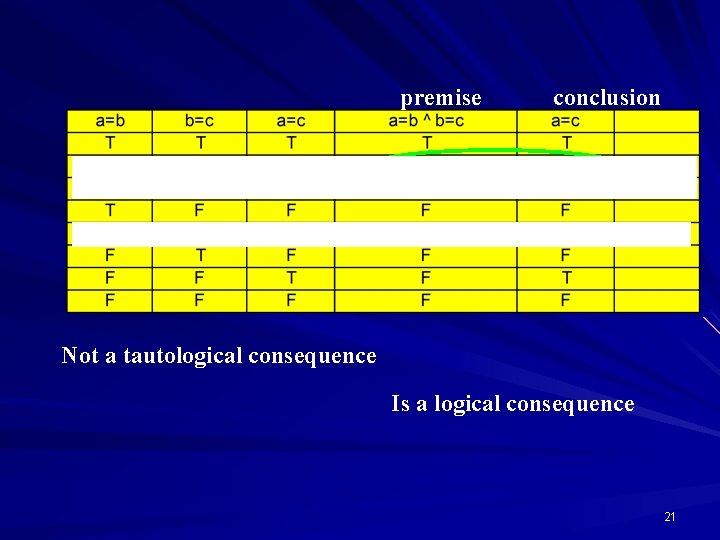
Logical Consequence Sentence Q is a logical consequence of P 1, P 2, …, Pn if and only if every nonspurious row that assigns true to all of the premises also assigns true to Q. 20

premise conclusion Not a tautological consequence Is a logical consequence 21

Summary Necessary Possible Equivalence Consequence S is always true S could be true S and S’ always have the same truth values Whenever P 1…Pn are true, Q is also true S is a tautology S is Tautologically possible S and S’ are Tautologically equivalent Q is a tautological consequence of P 1…Pn Logical S is logically All non-spurious necessary (logical truth) rows S is logically possible S and S’ are logically equivalent Q is a logical consequence of P 1…Pn TW Logic + Tarski’s World S is TW possible S and S’ are TW equivalent Q is a TWconsequence of P 1…Pn Tautological All rows in truth table S is TW necessary 22

Summary Logical-Consequences of P 1…Pn Tautological. Consequences of P 1…Pn Every tautological consequence of a set of premises is a logical consequence of these premises. Not every logical consequence of a set of premises is a tautological consequence of these premises. 23

Summary Every tautological equivalence is a logical equivalence. Not every logical equivalence is a tautological equivalence. Logical Equivalences Tautological Equivalences 24

Summary Every tautology is a logical necessity. Not every logical necessity is a tautology. Logical Necessities Tautologies 25