CS 148 Introduction to Computer Graphics and Imaging

CS 148: Introduction to Computer Graphics and Imaging 1/50 Transforms

2/50 © Louie Psihoyos http: //www. youtube. com/watch? v=46 mcpq. OVN 08

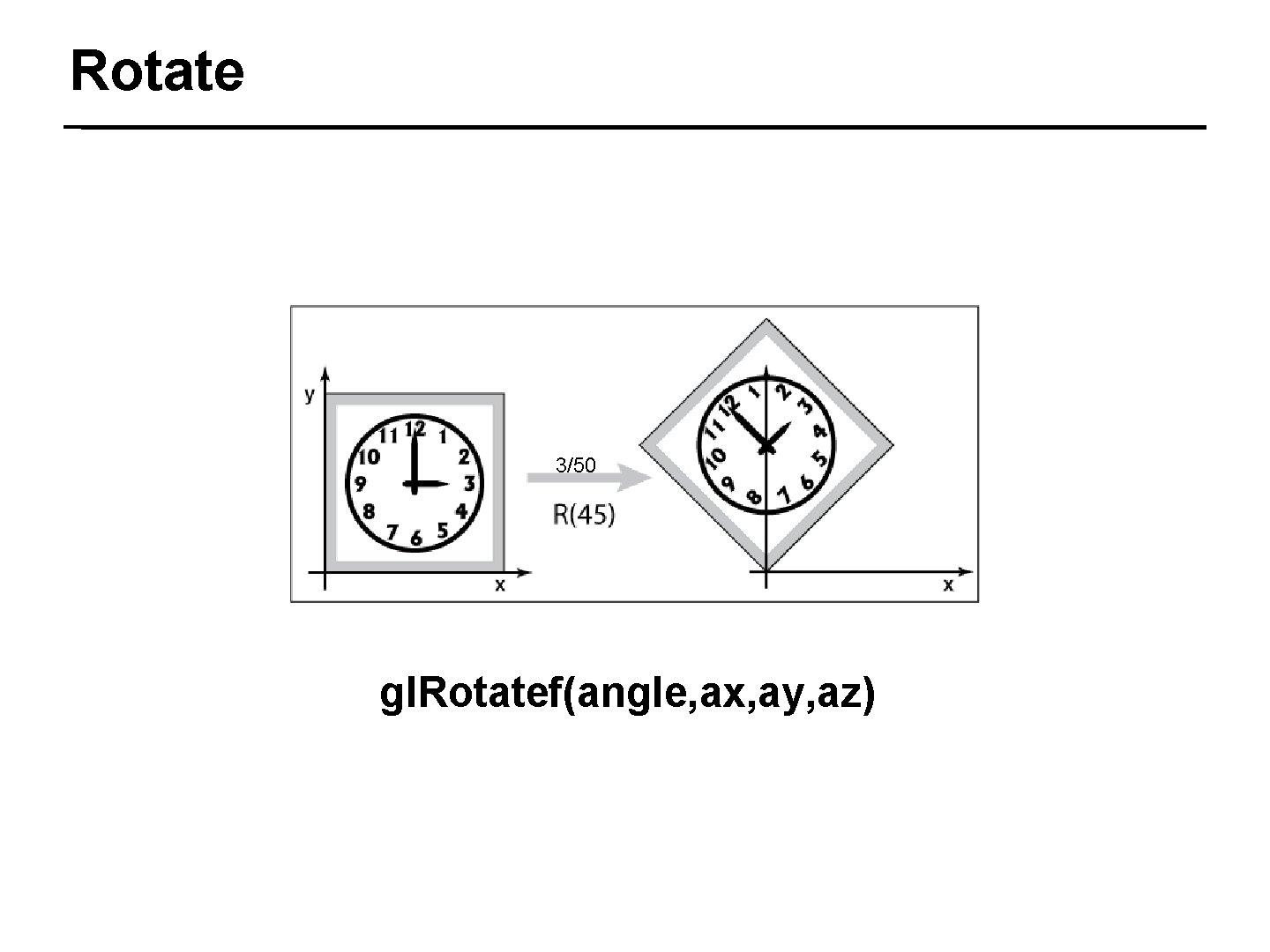
Rotate 3/50 gl. Rotatef(angle, ax, ay, az)

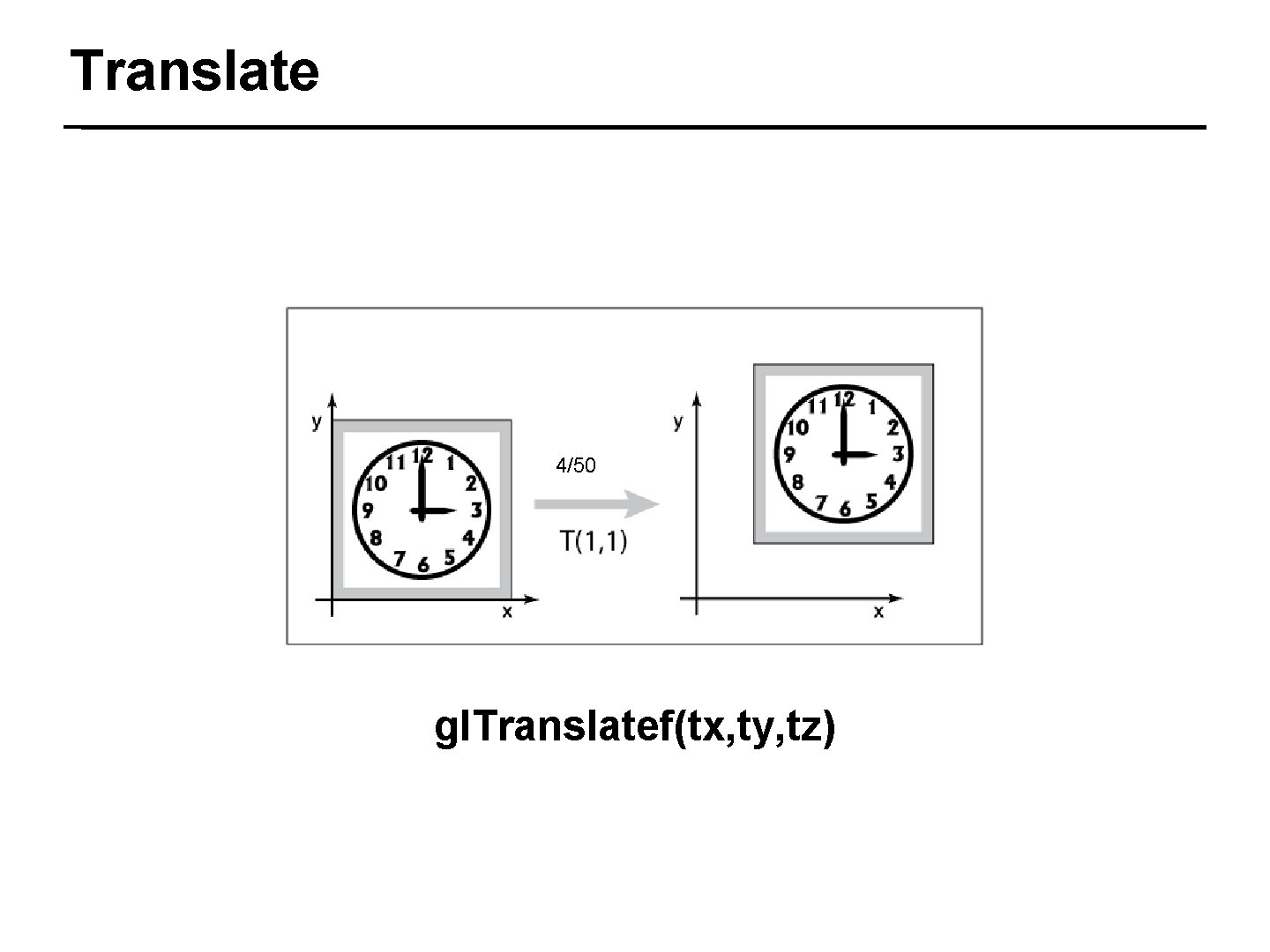
Translate 4/50 gl. Translatef(tx, ty, tz)

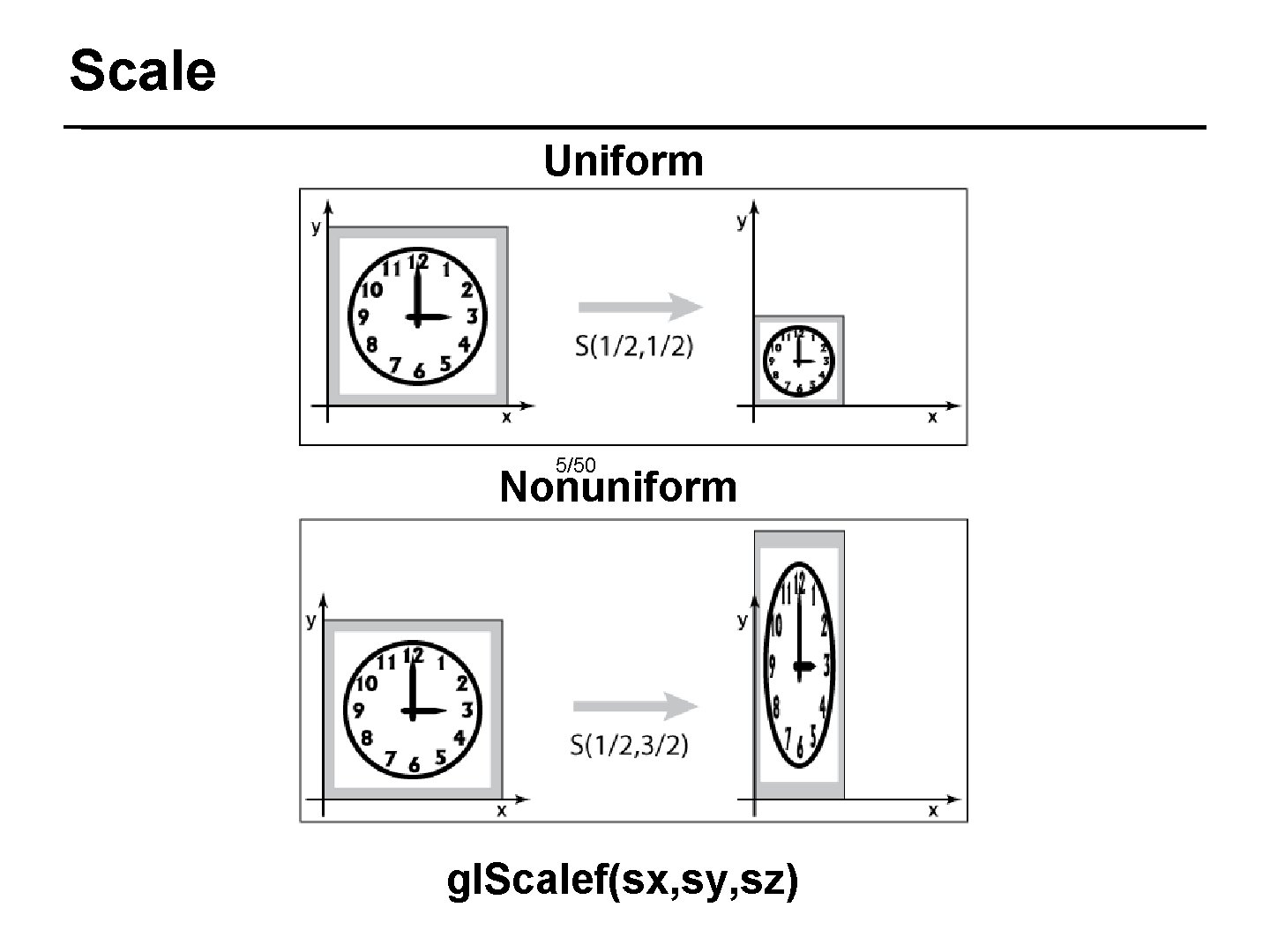
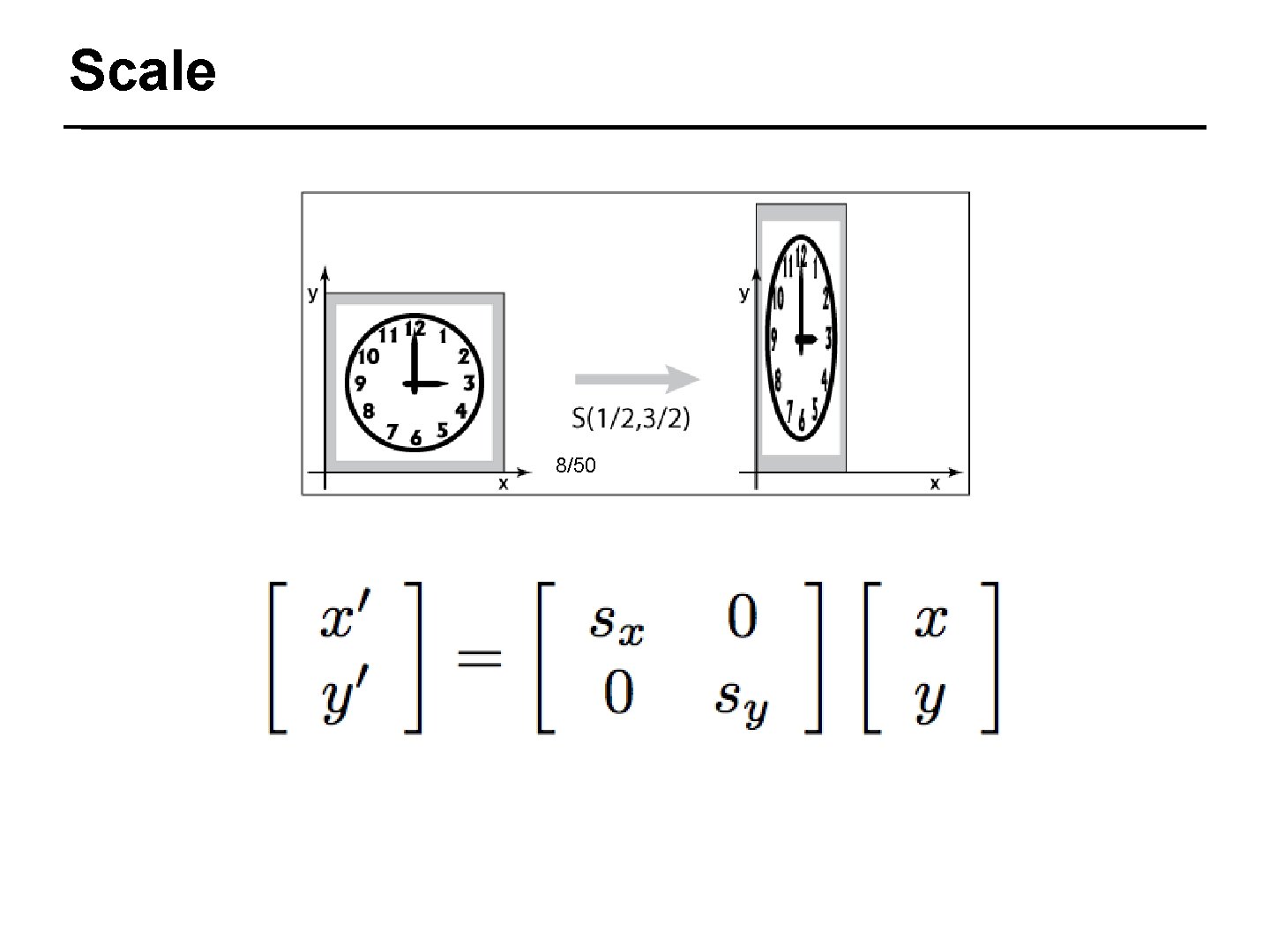
Scale Uniform 5/50 Nonuniform gl. Scalef(sx, sy, sz)

Transformations What? Just functions acting on points (x’, y’, z’) = T(x, y, z) P’ = T(P) Why? Viewing ￭ ￭ 6/50 Window coordinates to framebuffer coordinates Virtual camera: parallel/perspective projections Modeling ￭ ￭ ￭ Create objects in convenient coordinates Multiple instances of a prototype shape Kinematics of linkages/skeletons - characters/robots

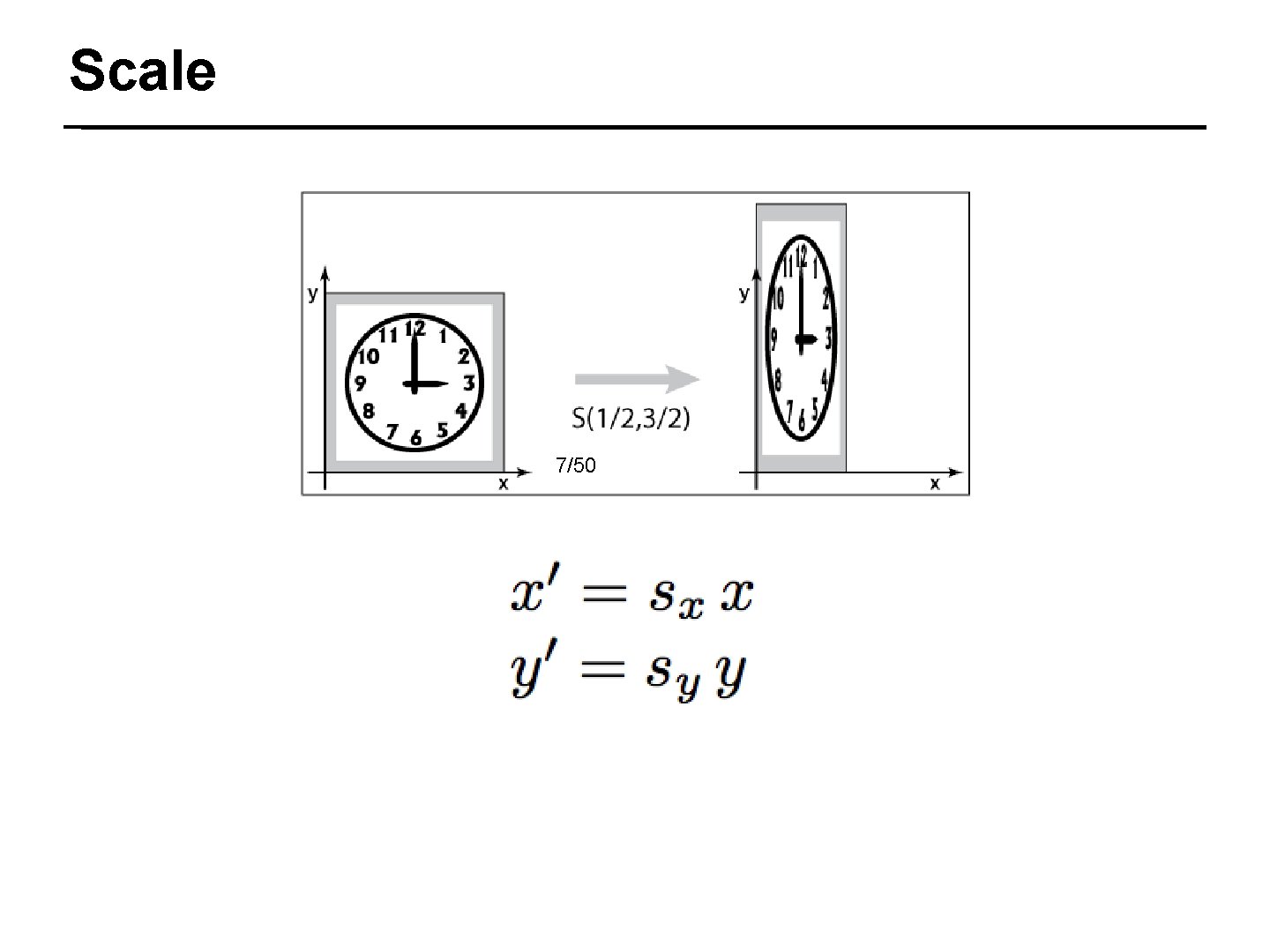
Scale 7/50

Scale 8/50

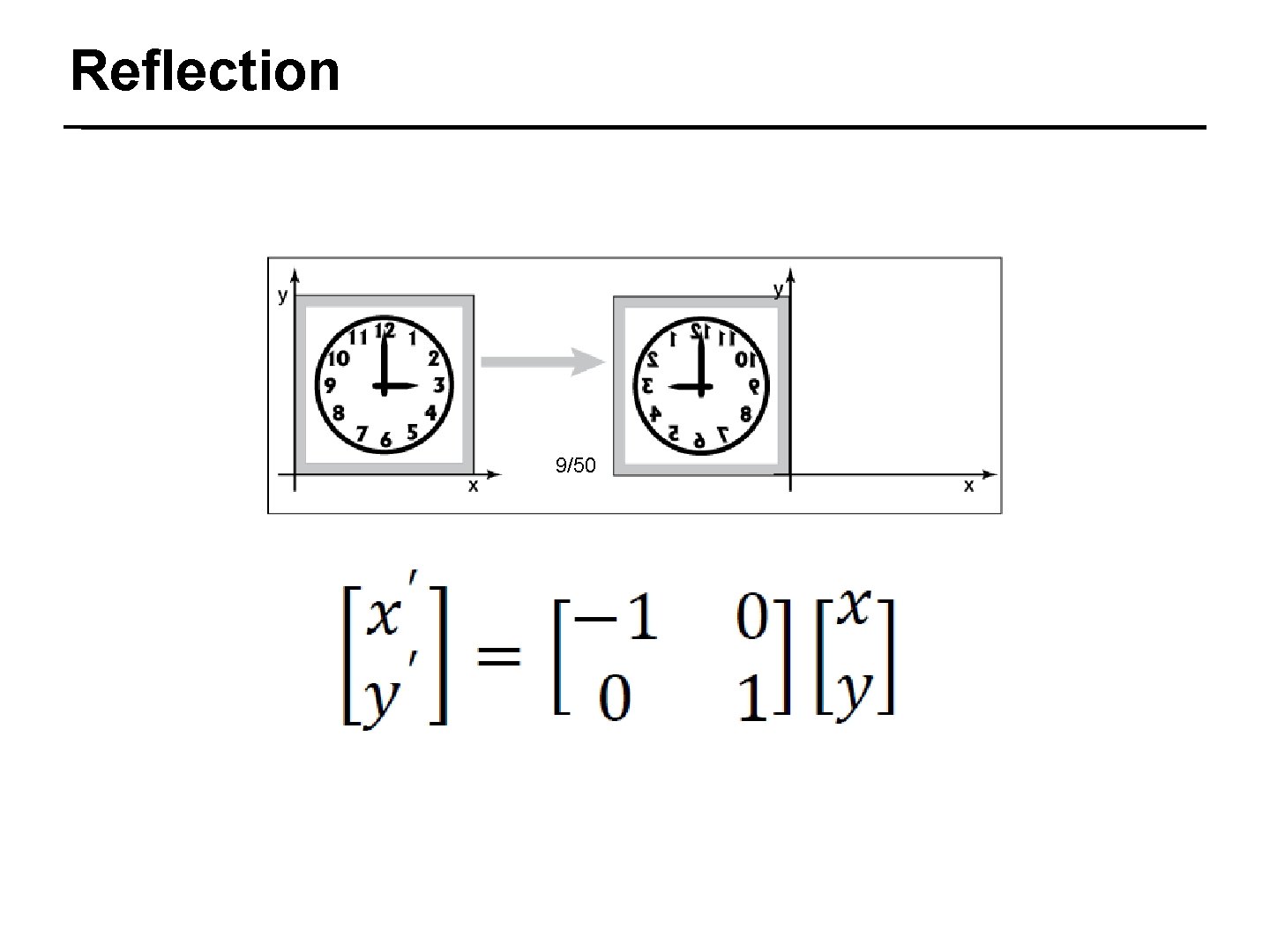
Reflection 9/50

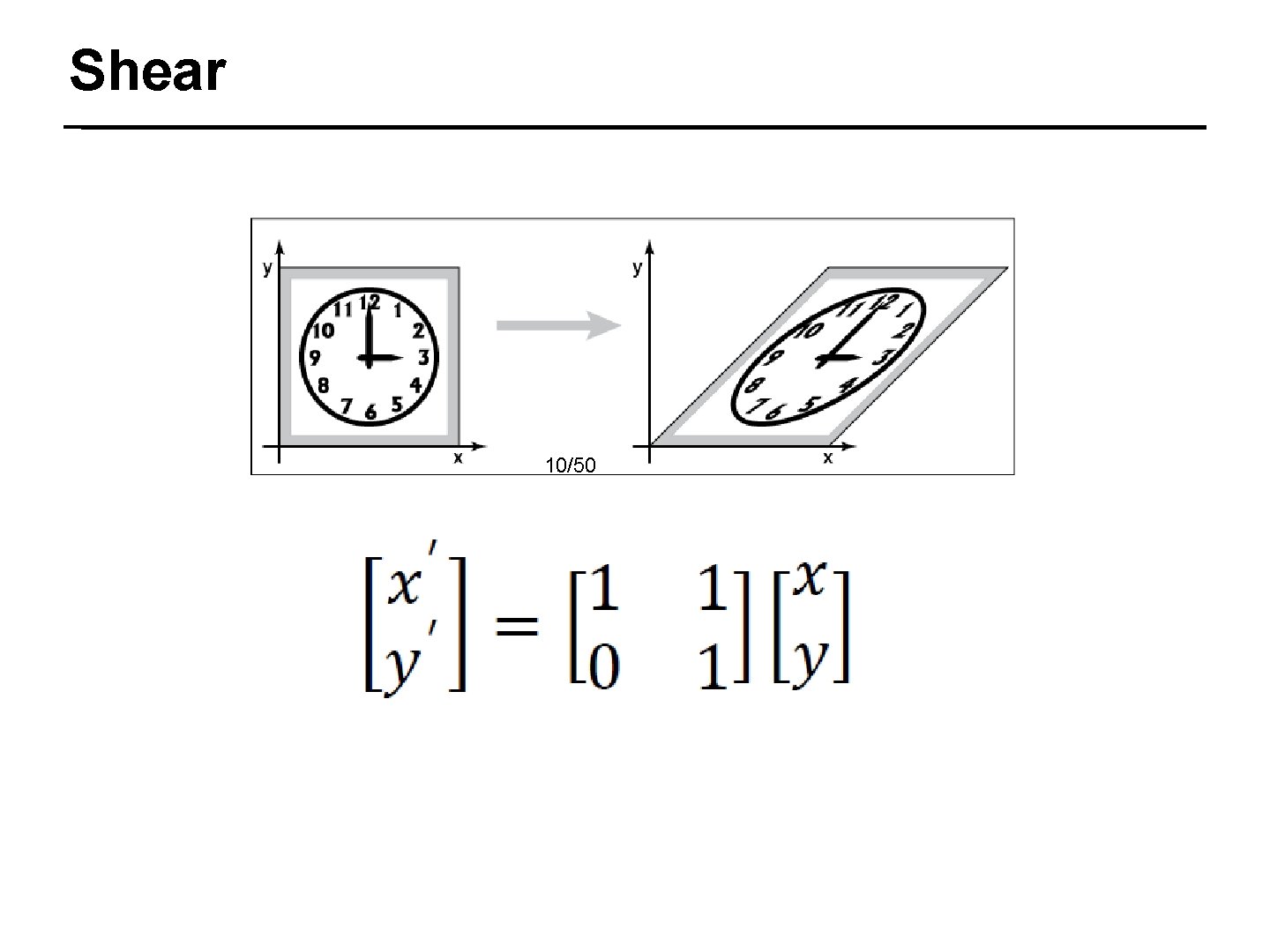
Shear 10/50

Linear Transform = Matrices 11/50

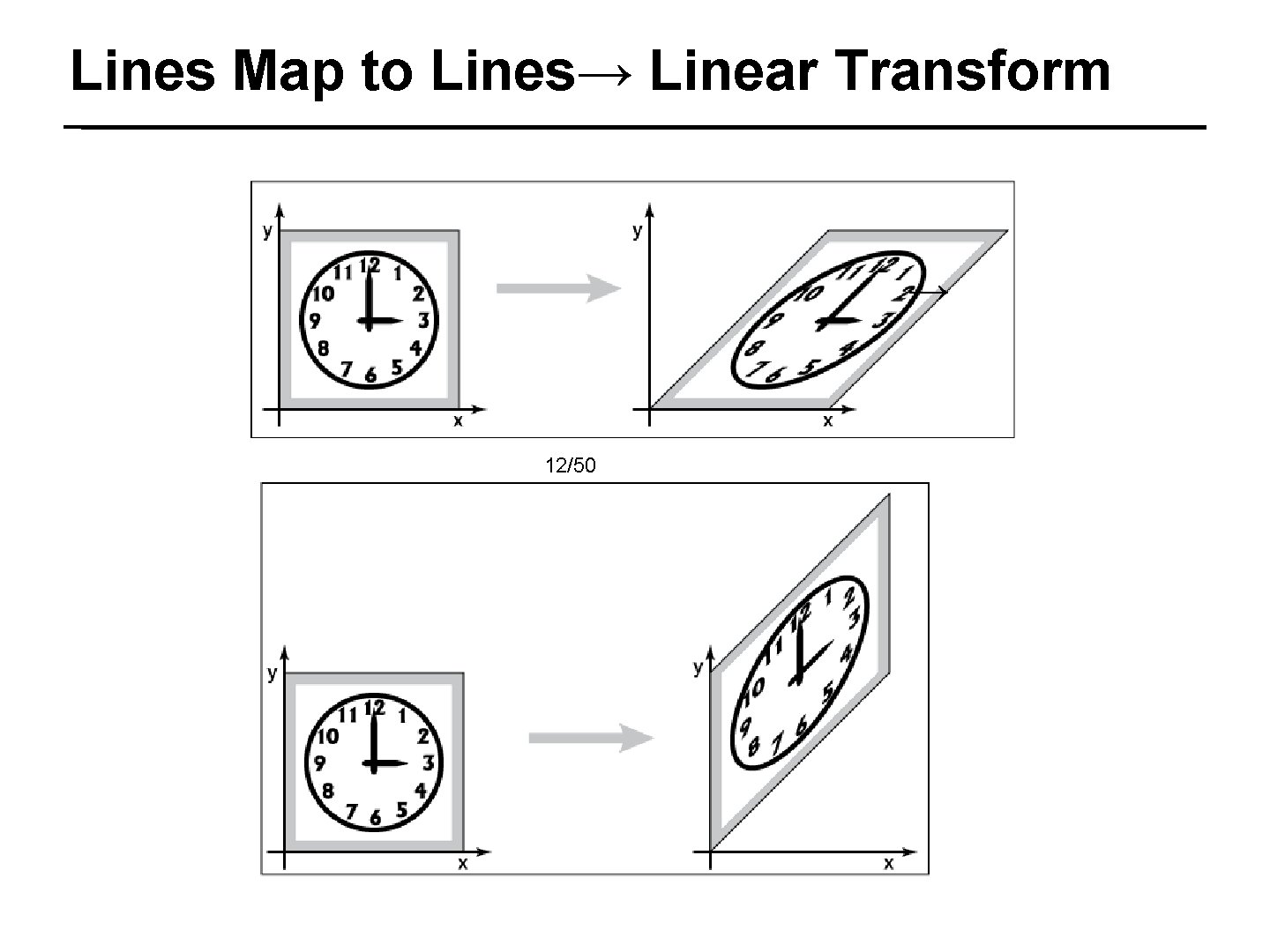
Lines Map to Lines→ Linear Transform → 12/50

13/50 Non-Linear Transform! Lines Map to Curves

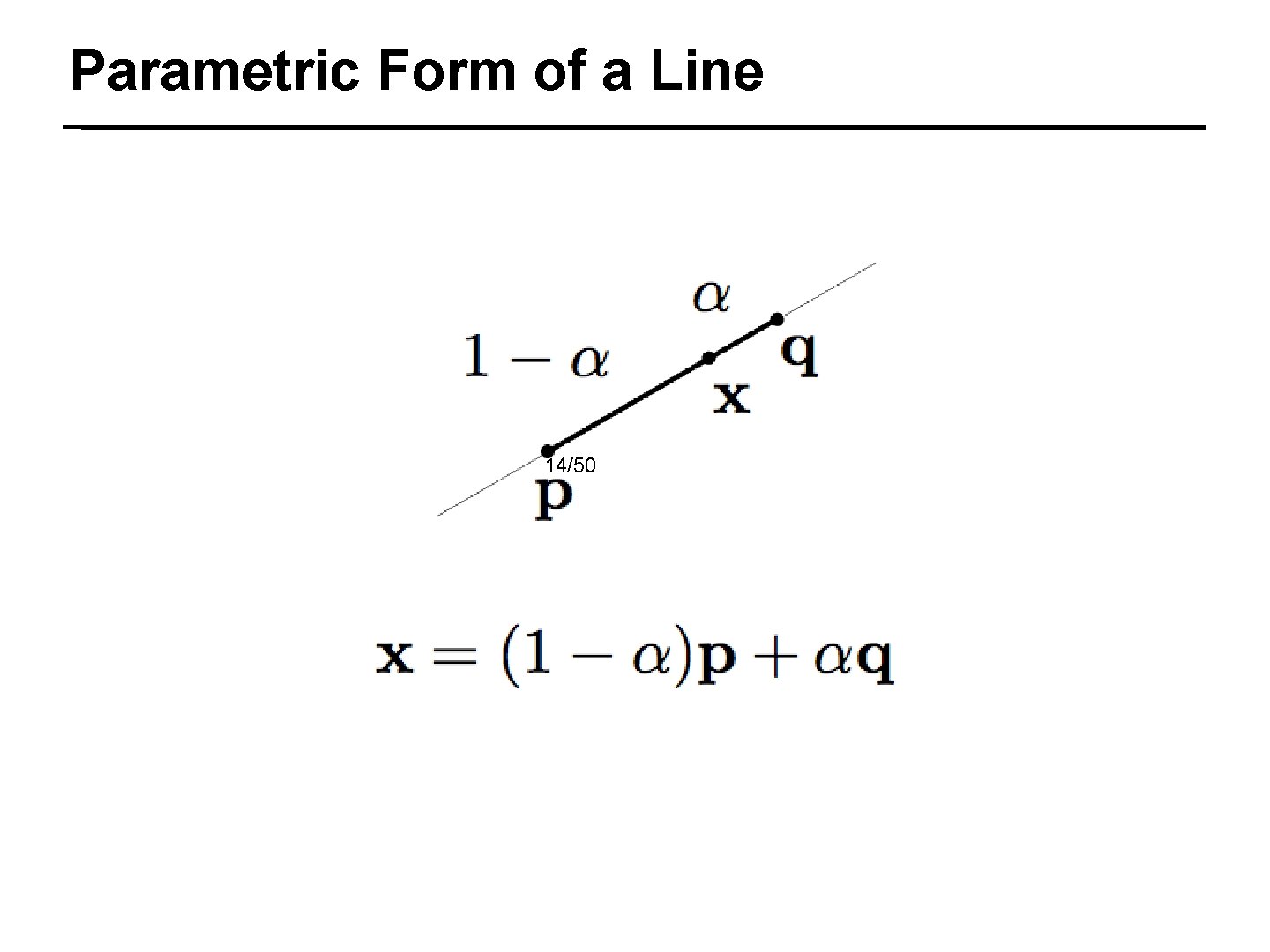
Parametric Form of a Line 14/50

Linear Transform→ Lines Map to Lines Start with the parametric form of a line Transform all the points on the line 15/50 Thus, a line transforms into a linear combination of transformed points, which is a line

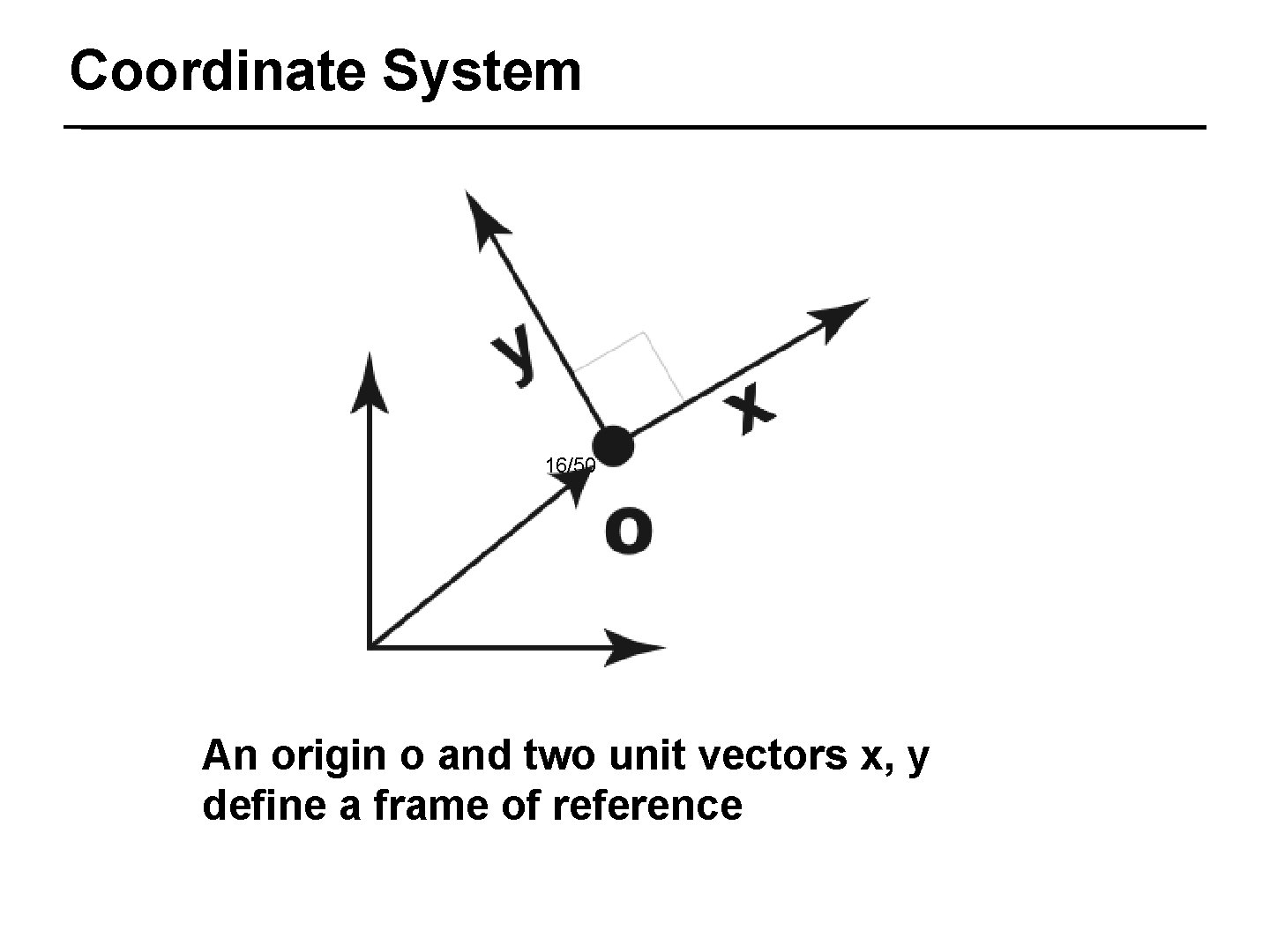
Coordinate System 16/50 An origin o and two unit vectors x, y define a frame of reference

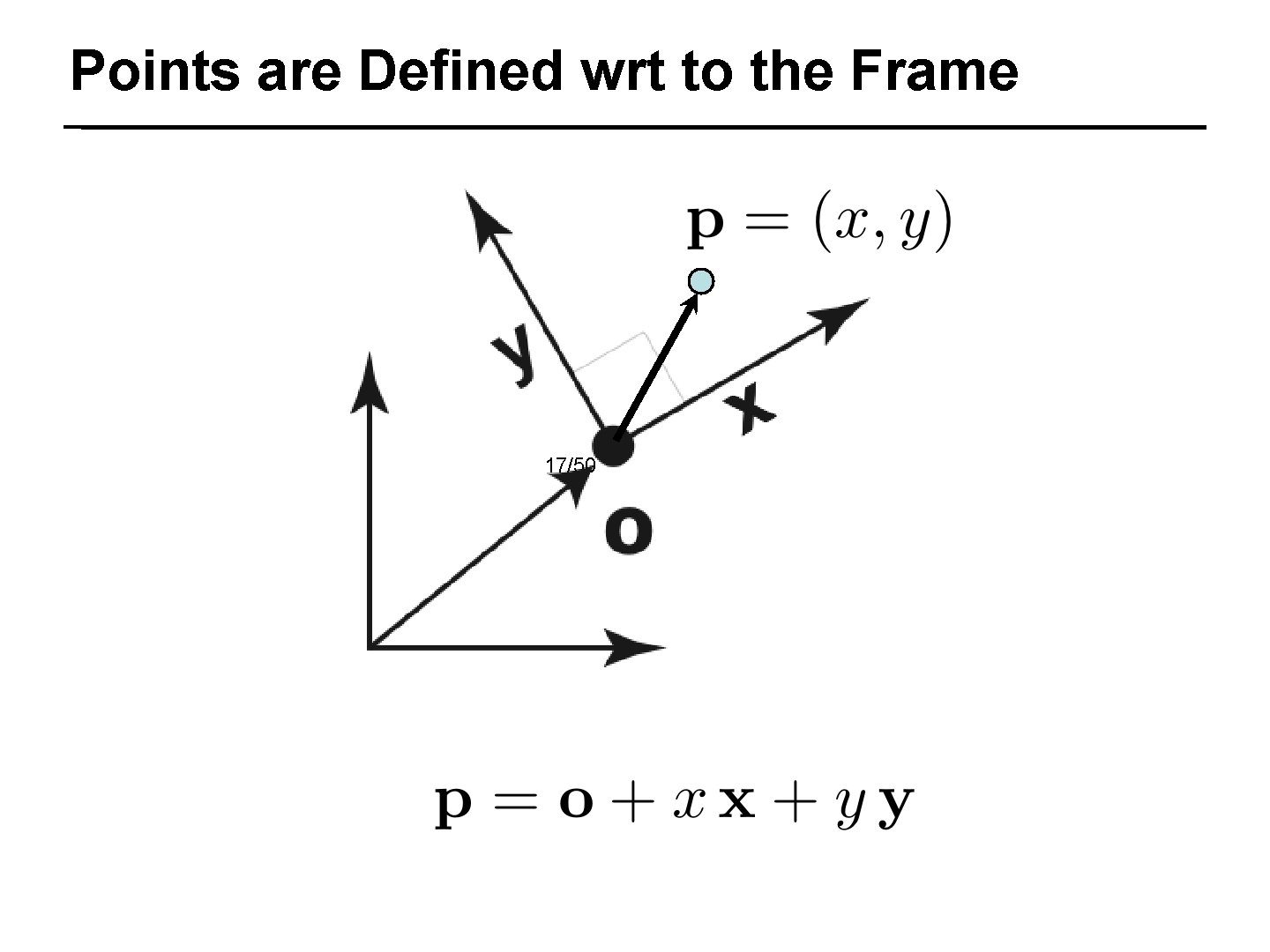
Points are Defined wrt to the Frame 17/50

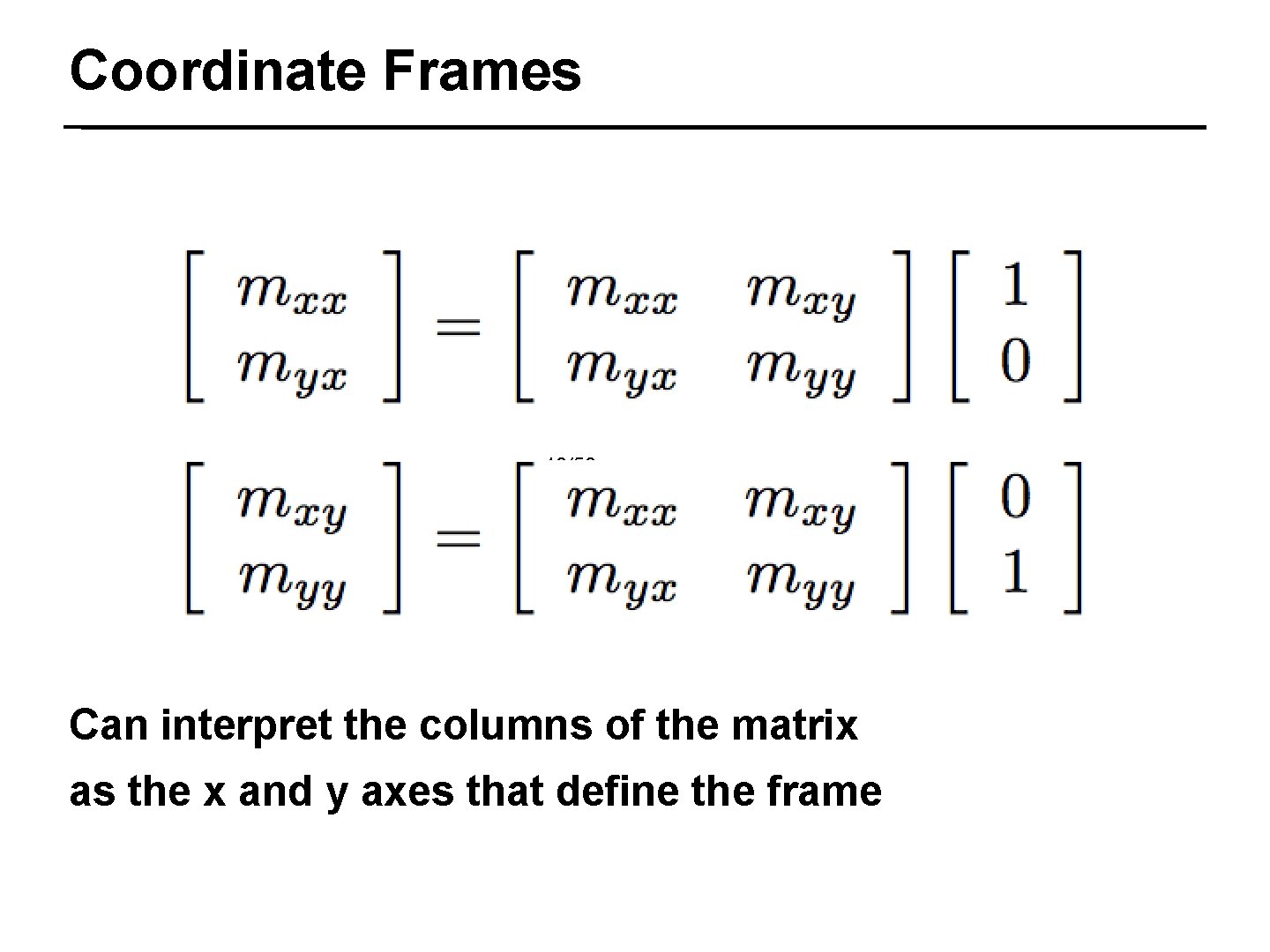
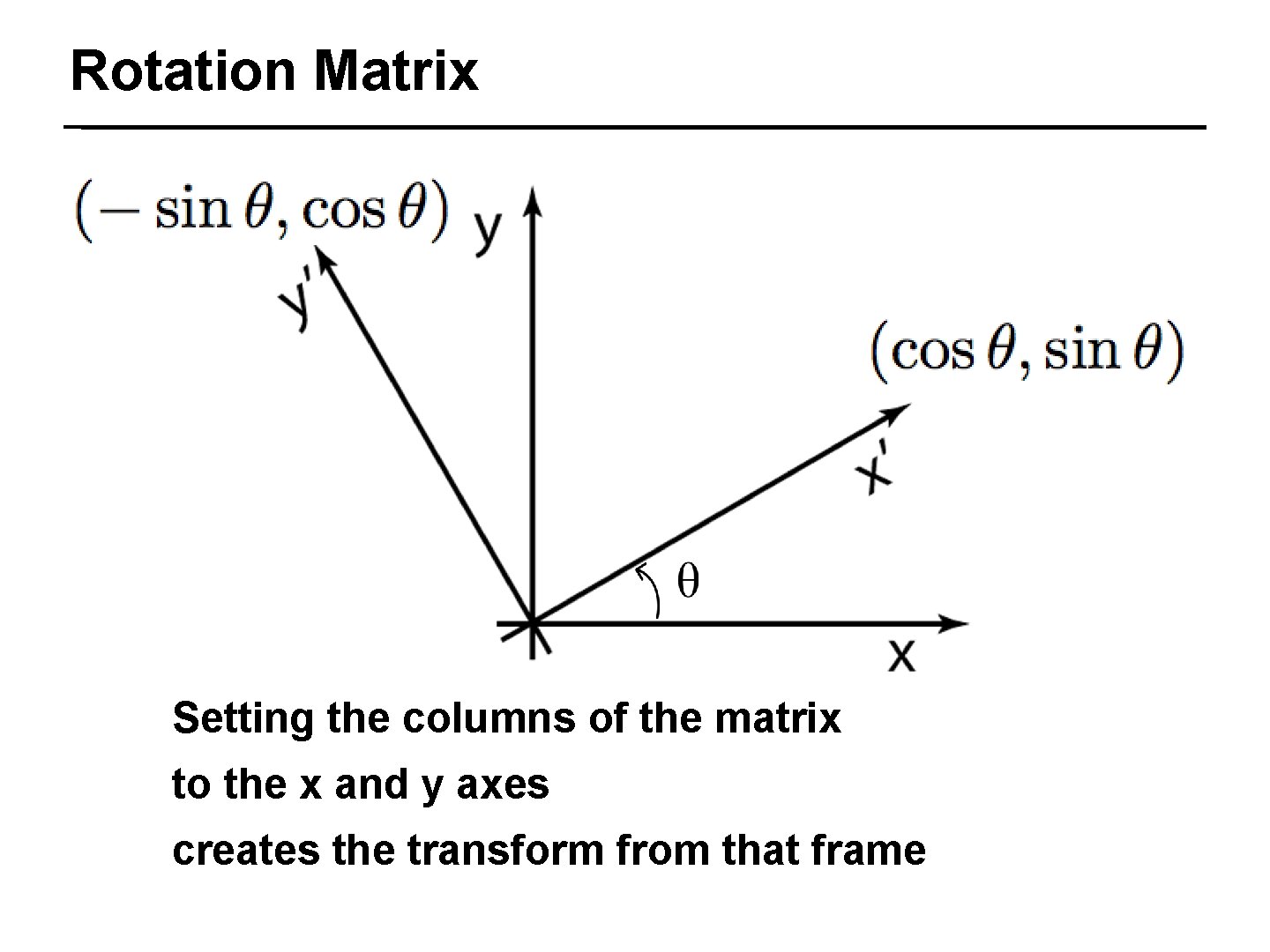
Coordinate Frames 18/50 Can interpret the columns of the matrix as the x and y axes that define the frame

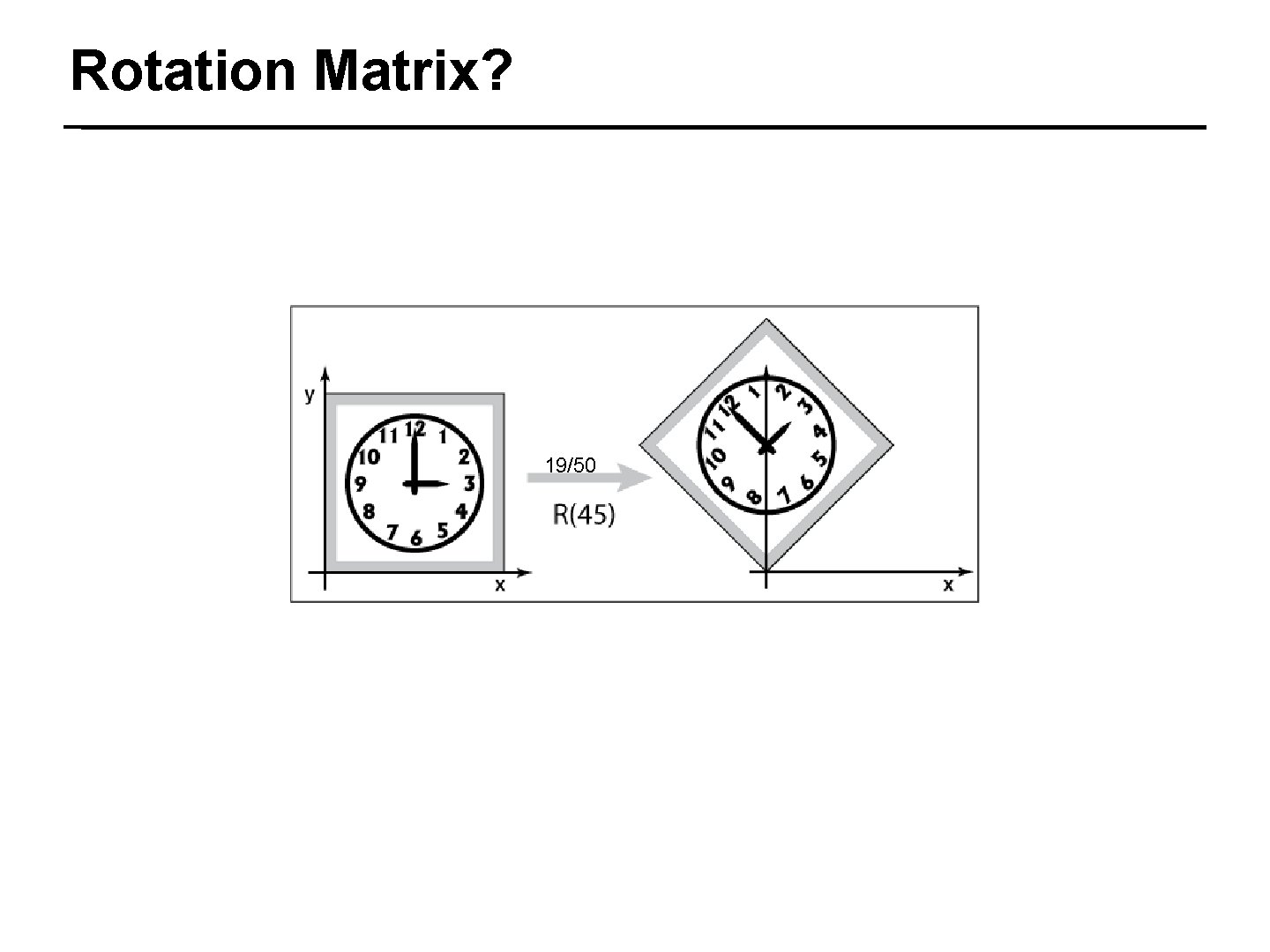
Rotation Matrix? 19/50

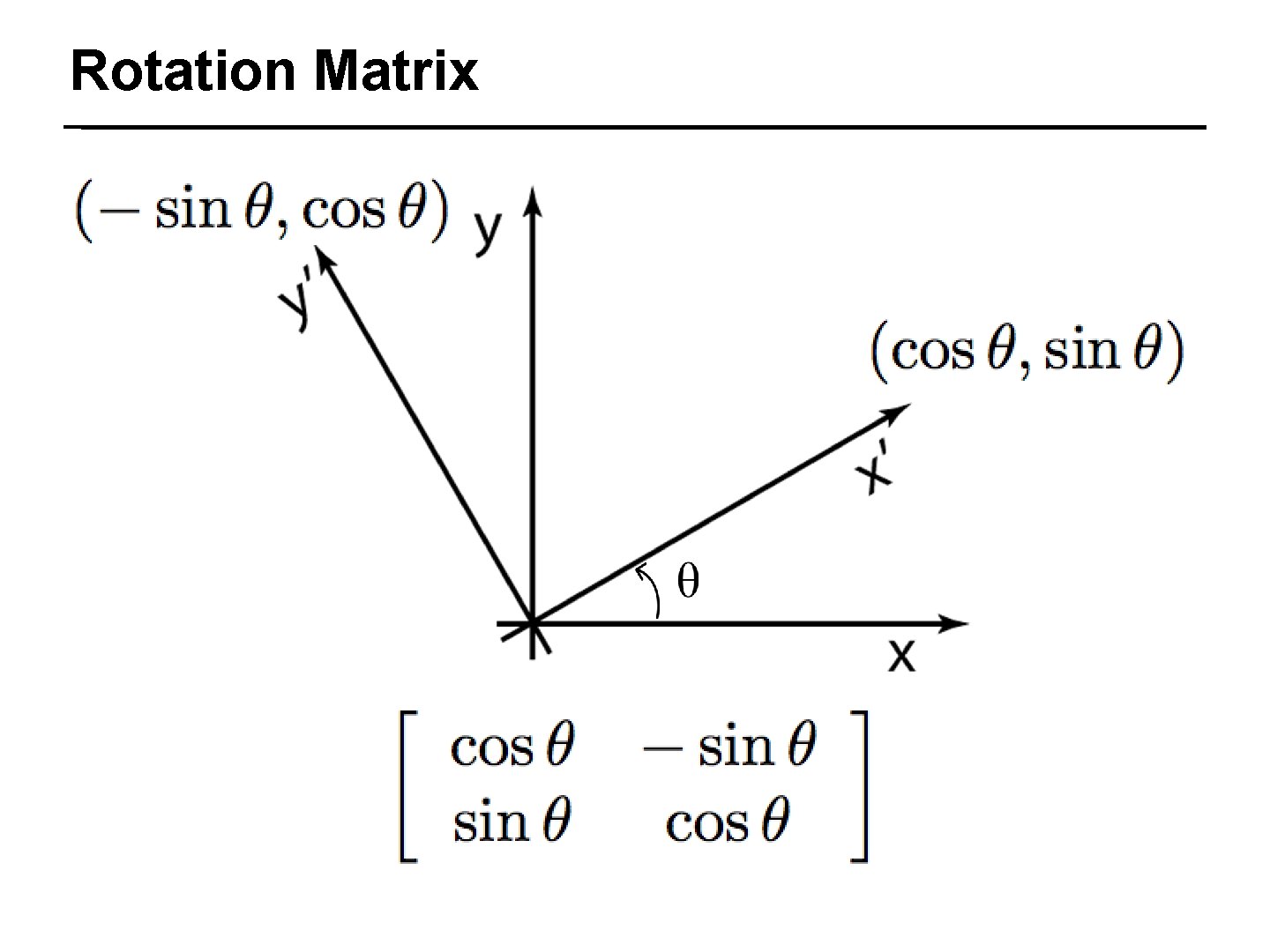
Rotation Matrix 20/50 Setting the columns of the matrix to the x and y axes creates the transform from that frame

Rotation Matrix 21/50

22/50

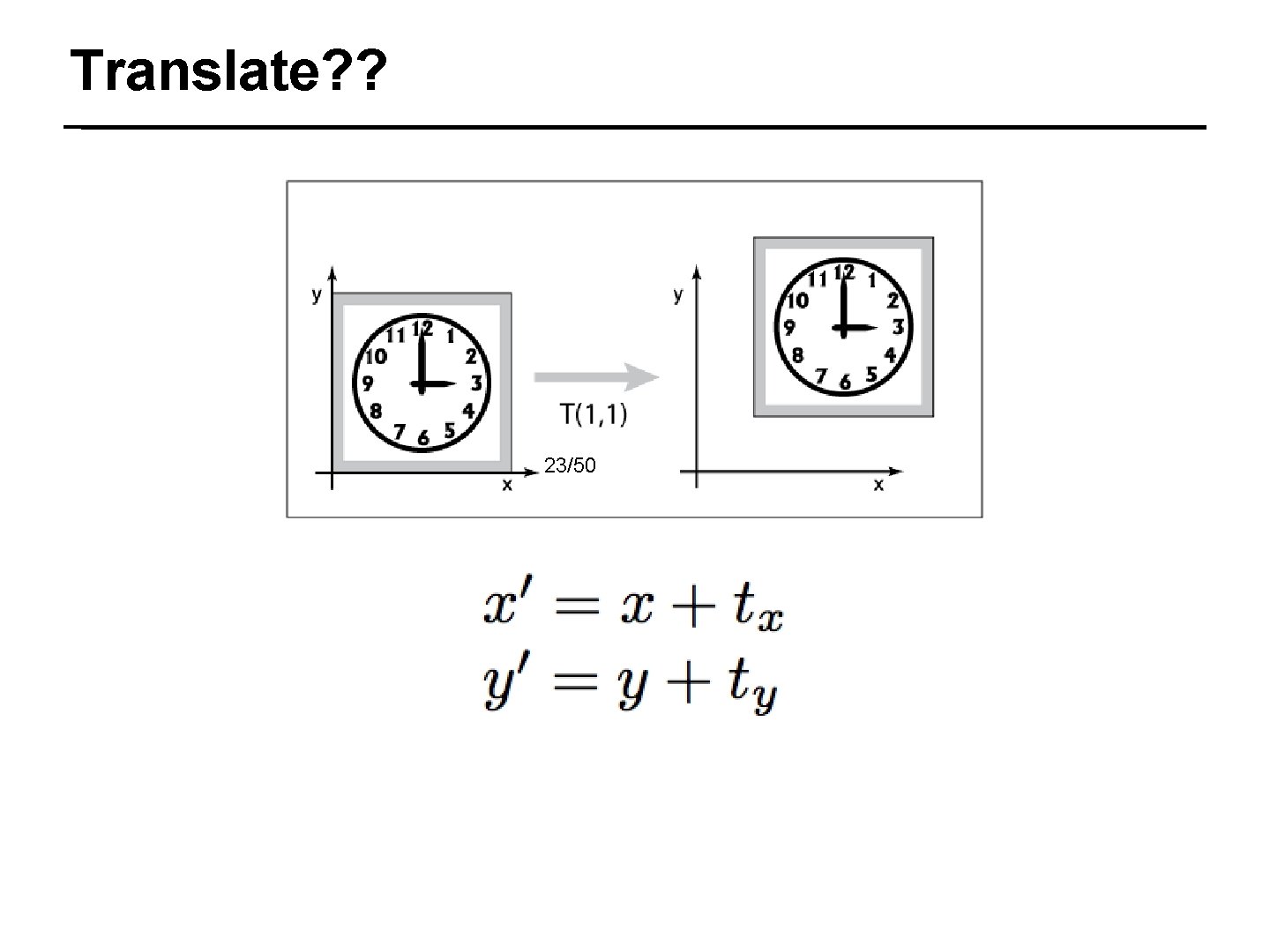
Translate? ? 23/50

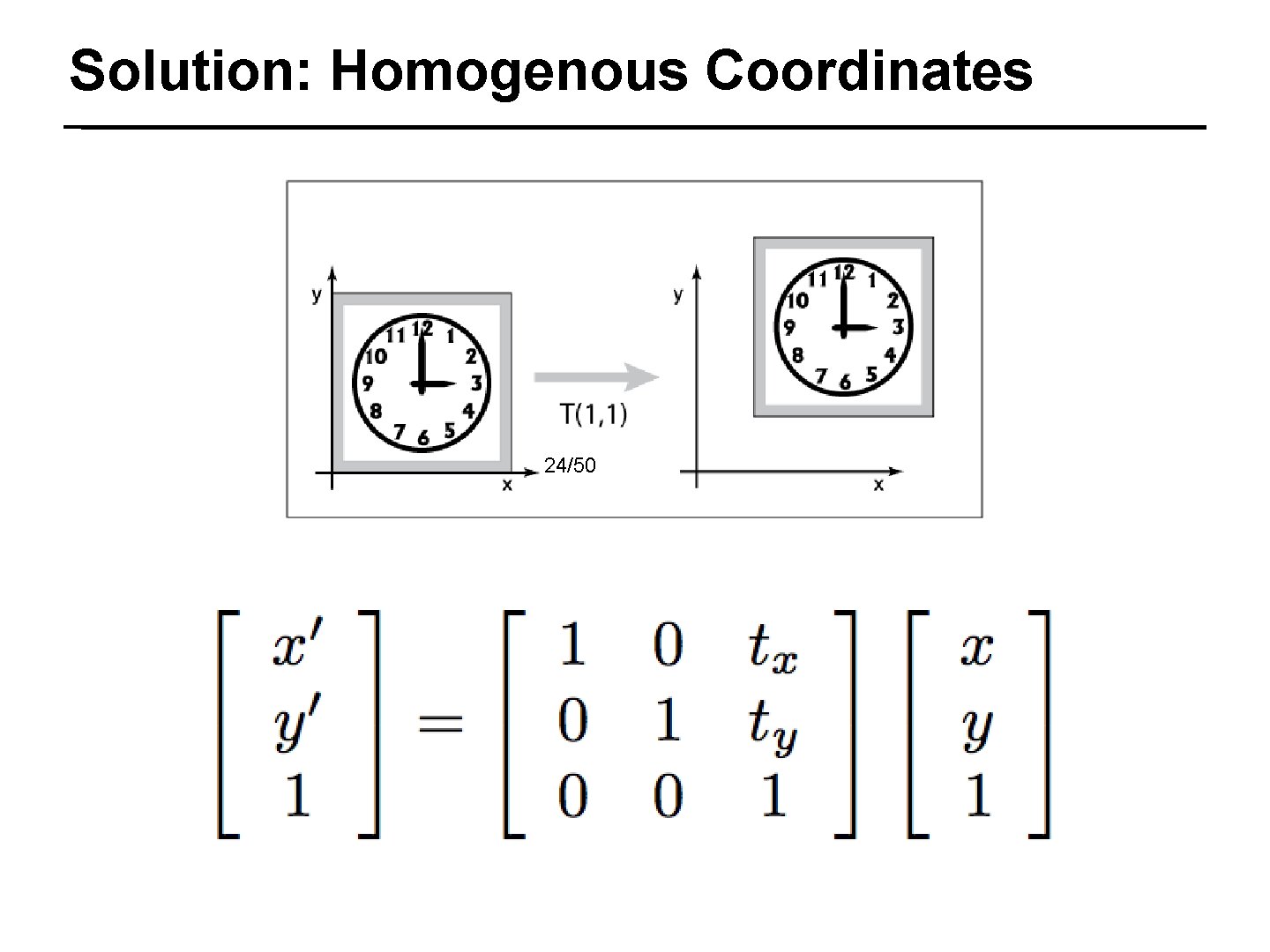
Solution: Homogenous Coordinates 24/50

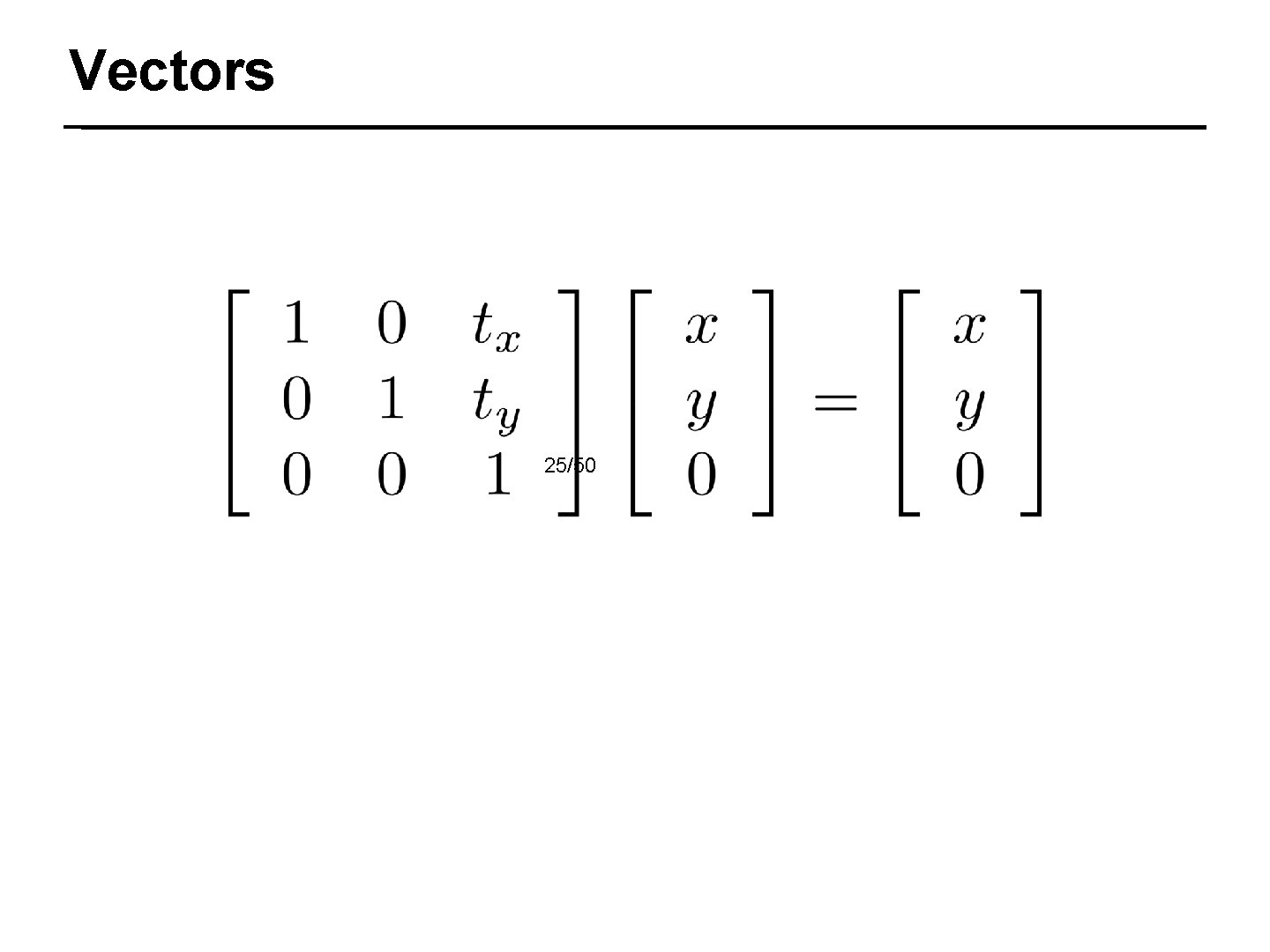
Vectors 25/50

Composing Transformations 26/50

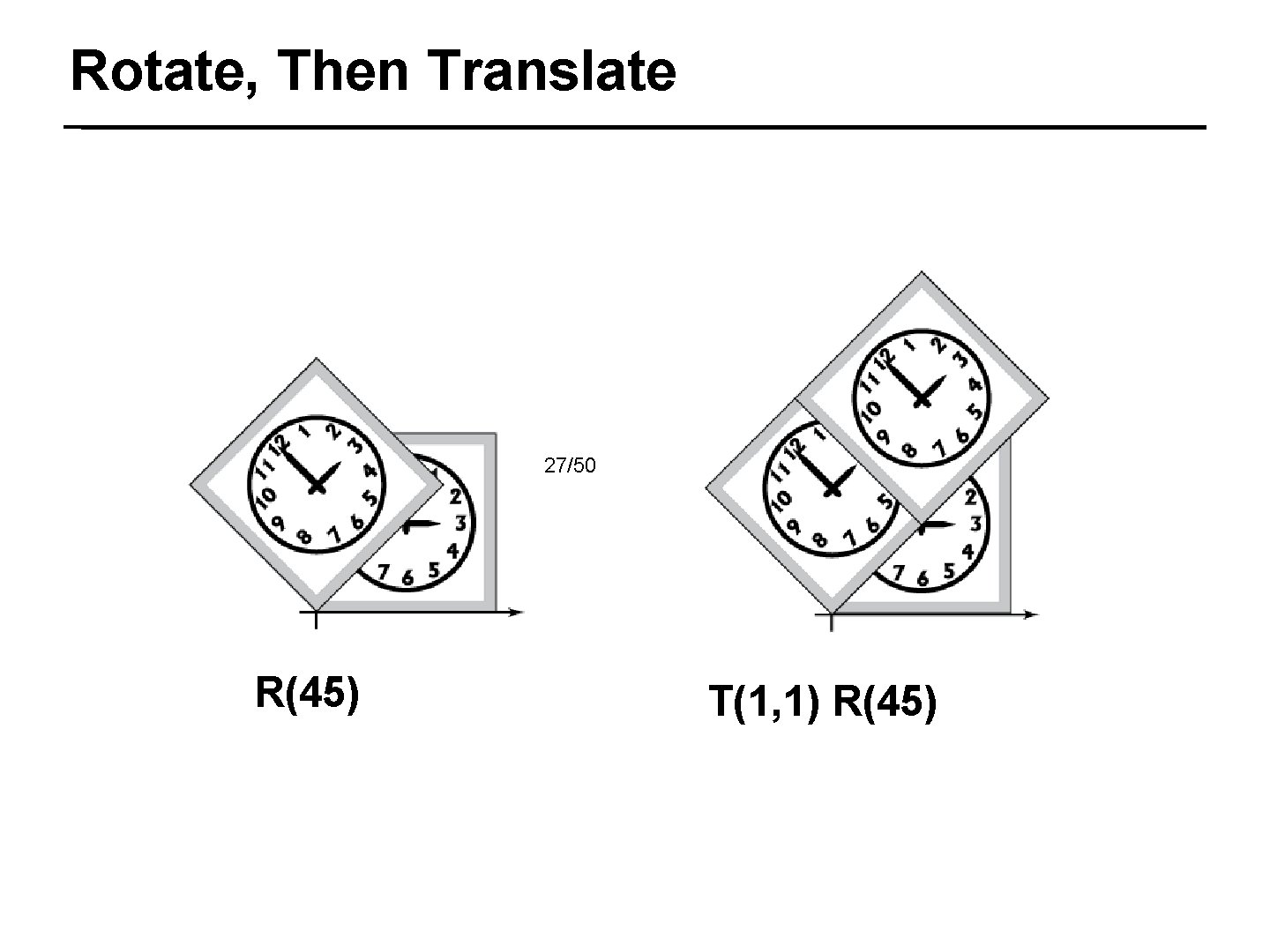
Rotate, Then Translate 27/50 R(45) T(1, 1) R(45)

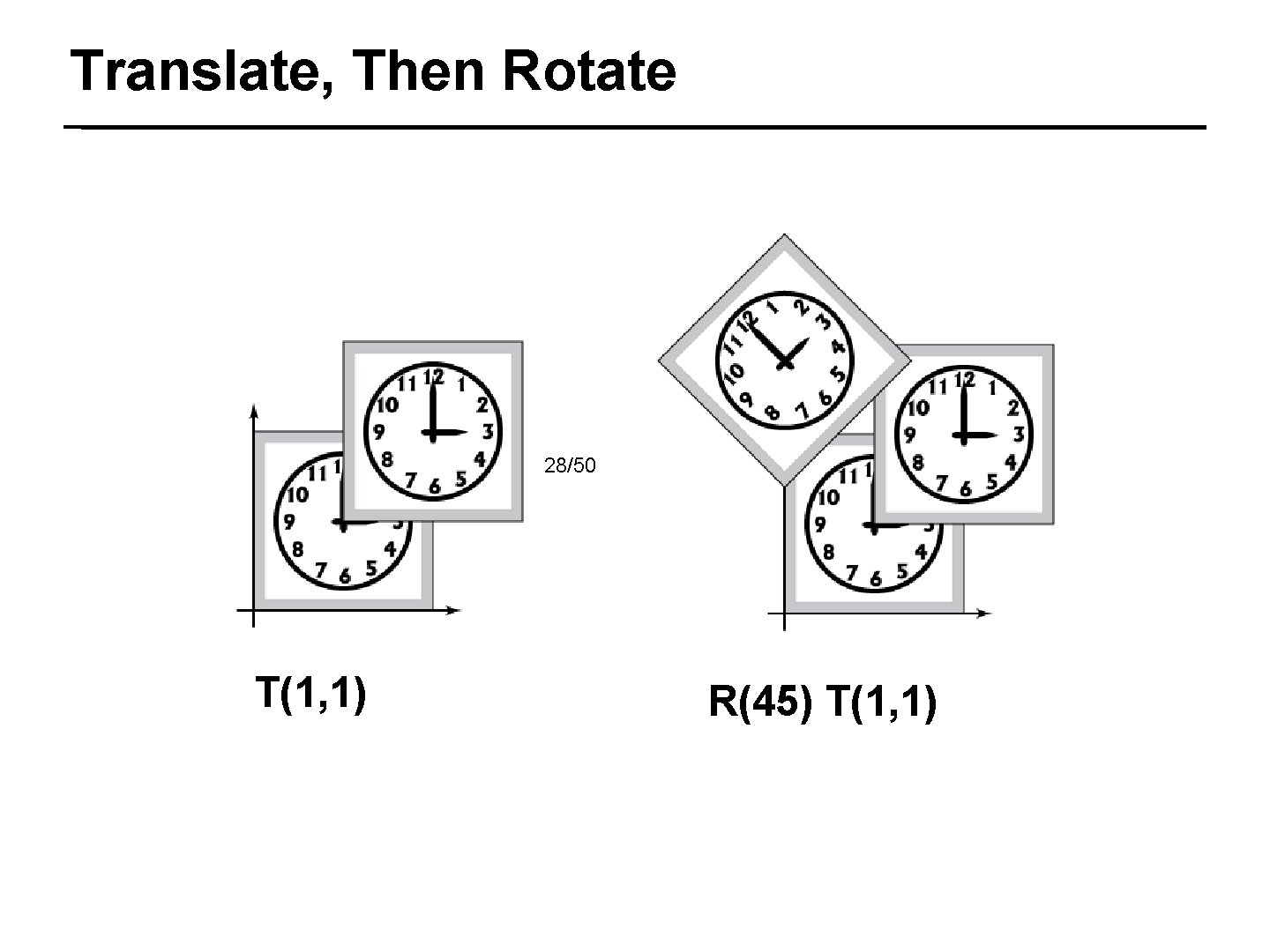
Translate, Then Rotate 28/50 T(1, 1) R(45) T(1, 1)

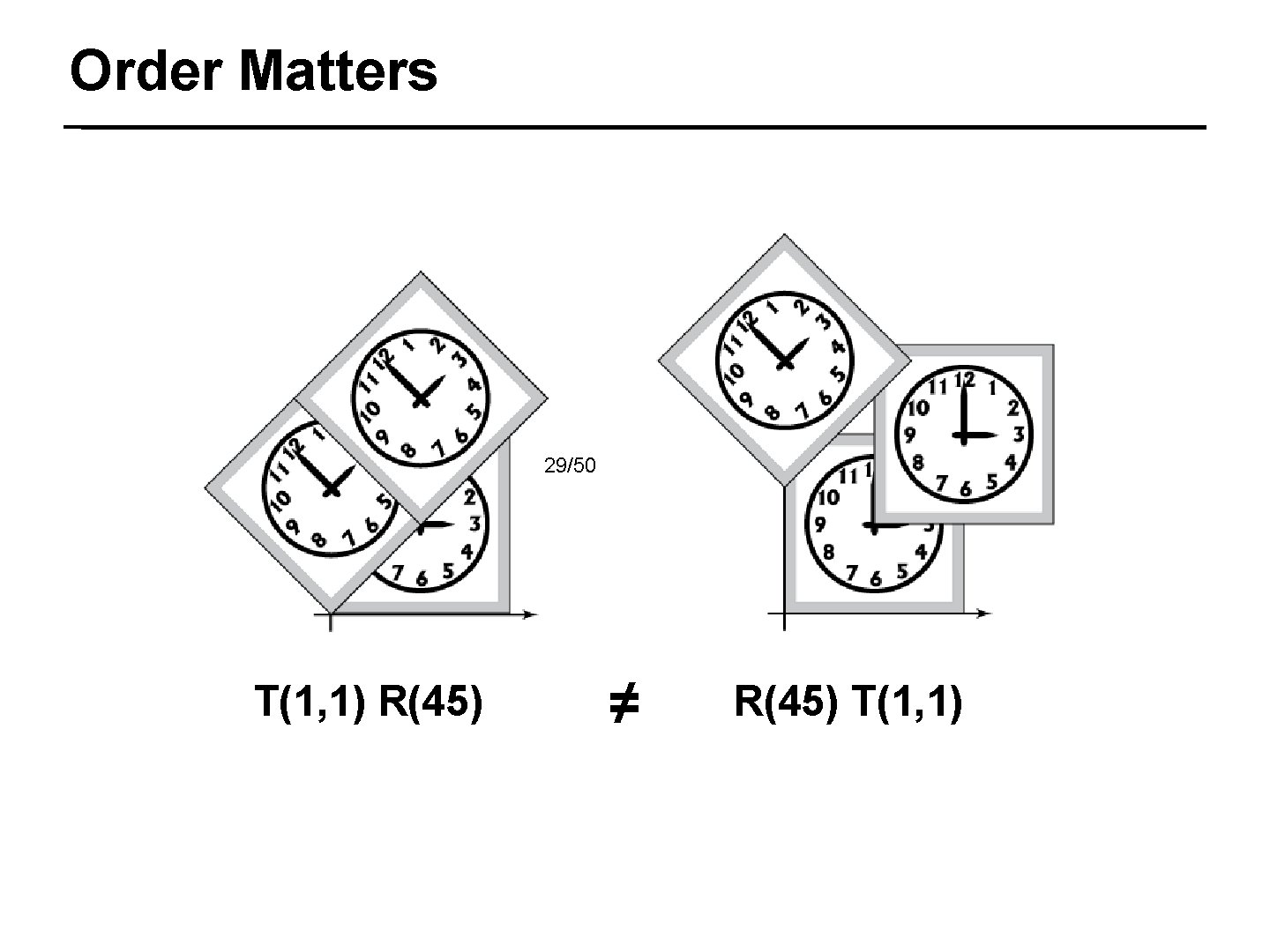
Order Matters 29/50 T(1, 1) R(45) ≠ R(45) T(1, 1)

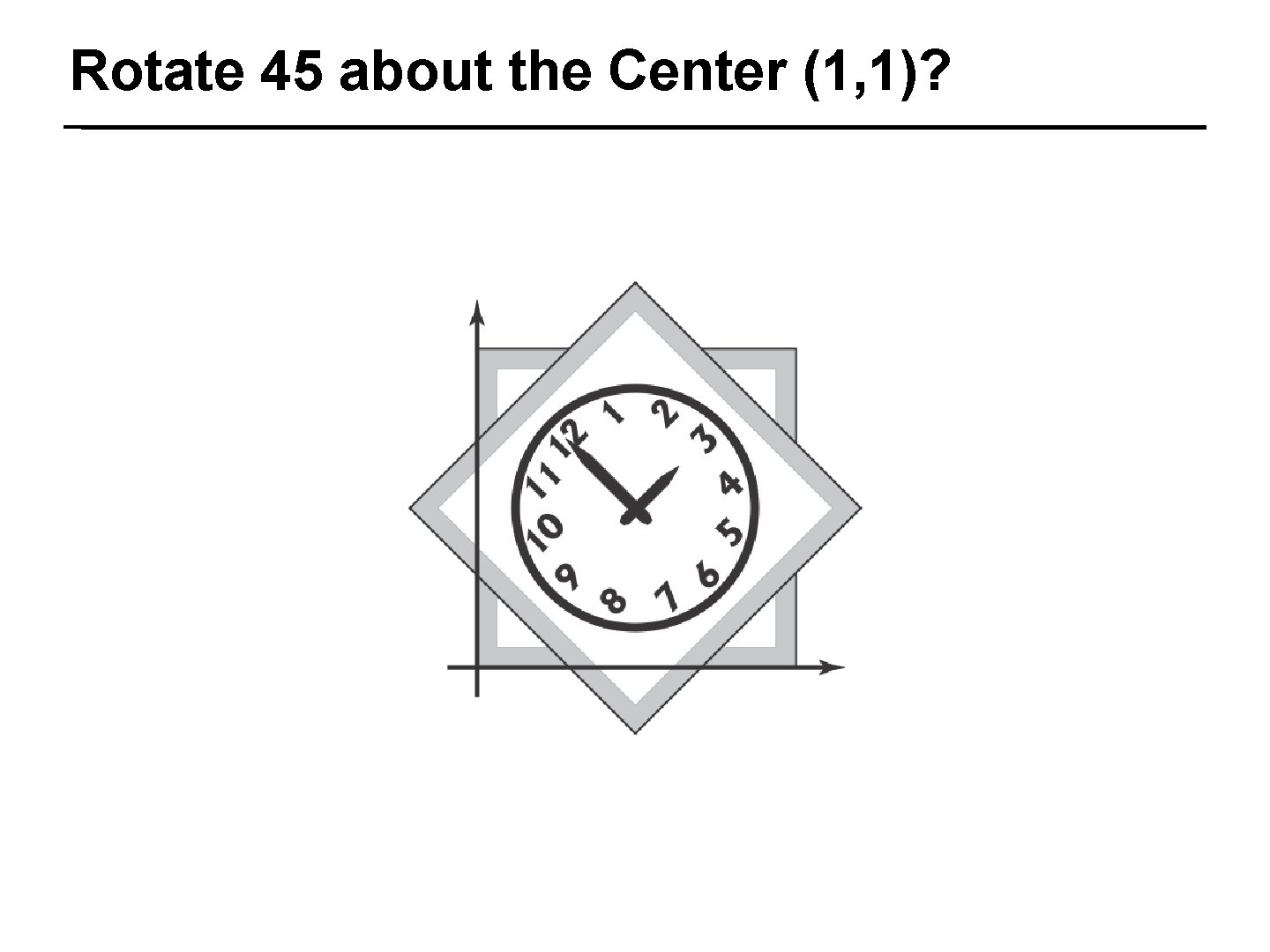
Rotate 45 about the Center (1, 1)? 30/50

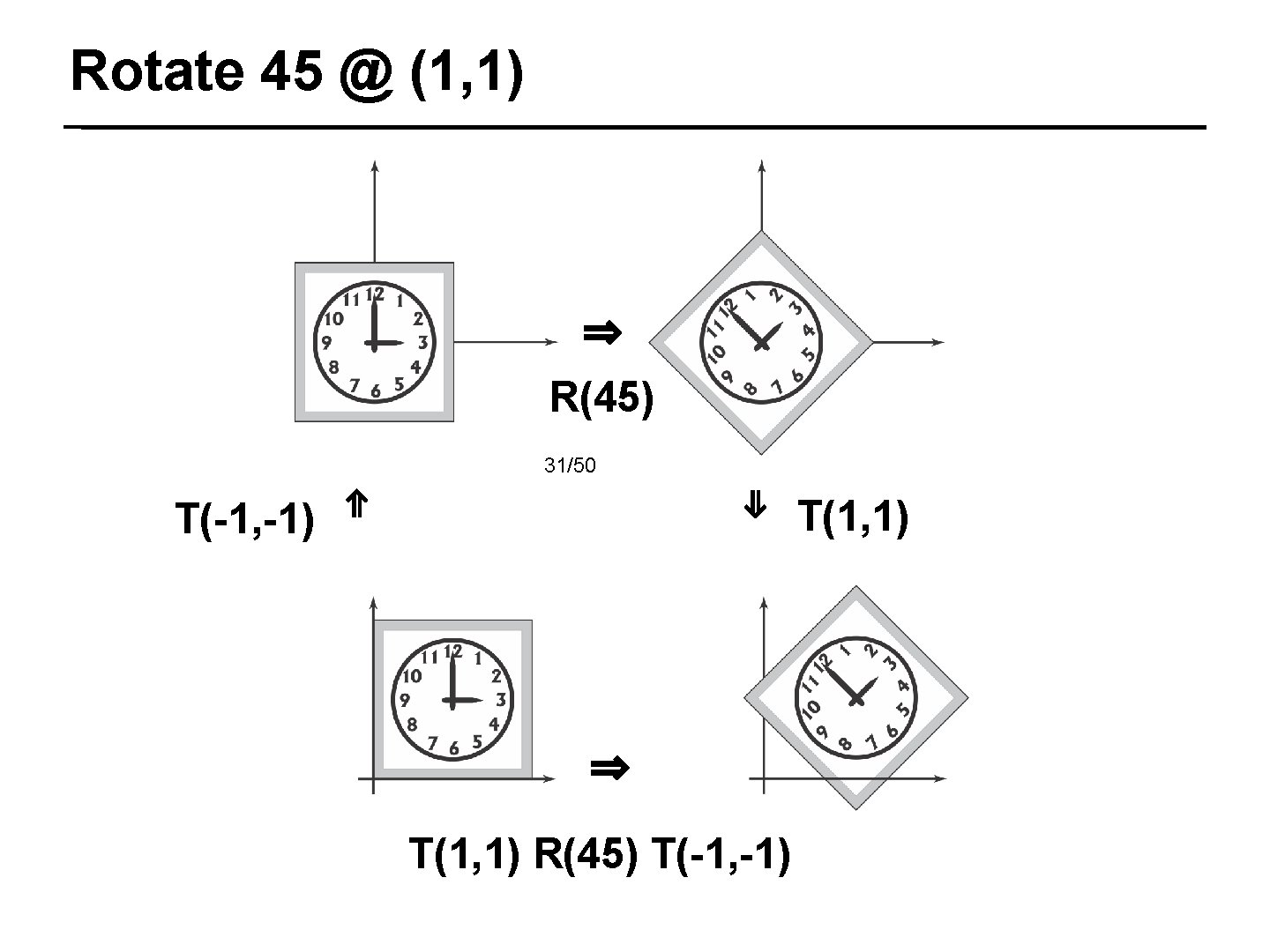
Rotate 45 @ (1, 1) ⇒ R(45) 31/50 ⇑ T(-1, -1) ⇓ T(1, 1) ⇒ T(1, 1) R(45) T(-1, -1)

Order of Transformations The rightmost transform is applied first P’ = T(1, 1) (R(45)(P)) That is, the rotate is applied before the translate 32/50 Open. GL gl. Translatef( 1. 0, 0. 0 ); gl. Rotatef( 45. 0, 0. , 1. ); The last gl call is applied first; we’ll see why later

Advantages of the Matrices Combine a sequence of transforms into a single transform P’ = A ( B ( C ( D ( p ) ) =(ABCD)P =MP 33/50 Why? Matrix multiplication is associative Advantages ￭ ￭ ￭ Very inefficient to recompute the matrix entries Very inefficient to multiply matrix times point multiple times Compute the matrix M once and then apply that matrix to many points

Transforming Points vs. 34/50 Transforming Coordinate Systems

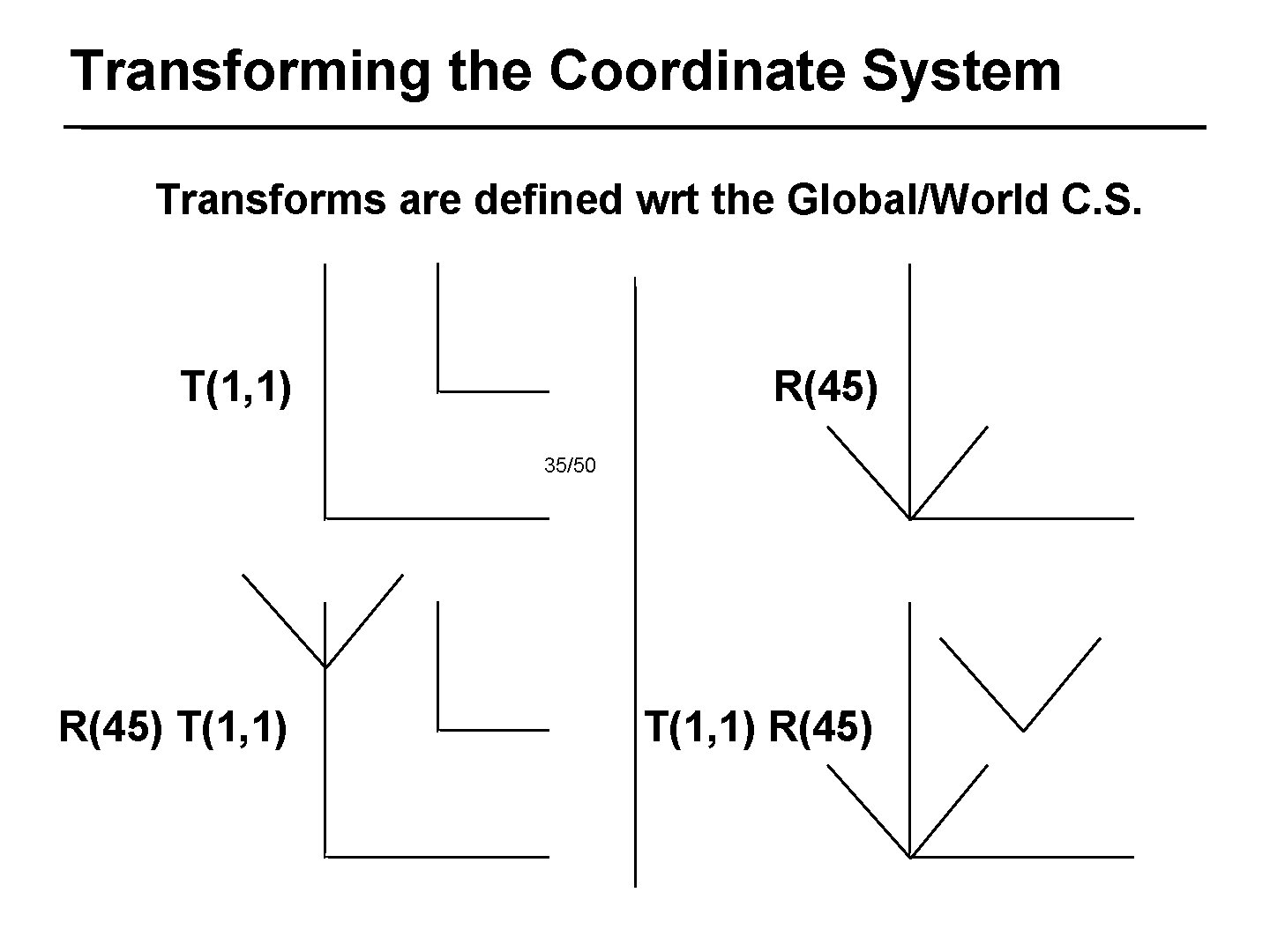
Transforming the Coordinate System Transforms are defined wrt the Global/World C. S. T(1, 1) R(45) 35/50 R(45) T(1, 1) R(45)

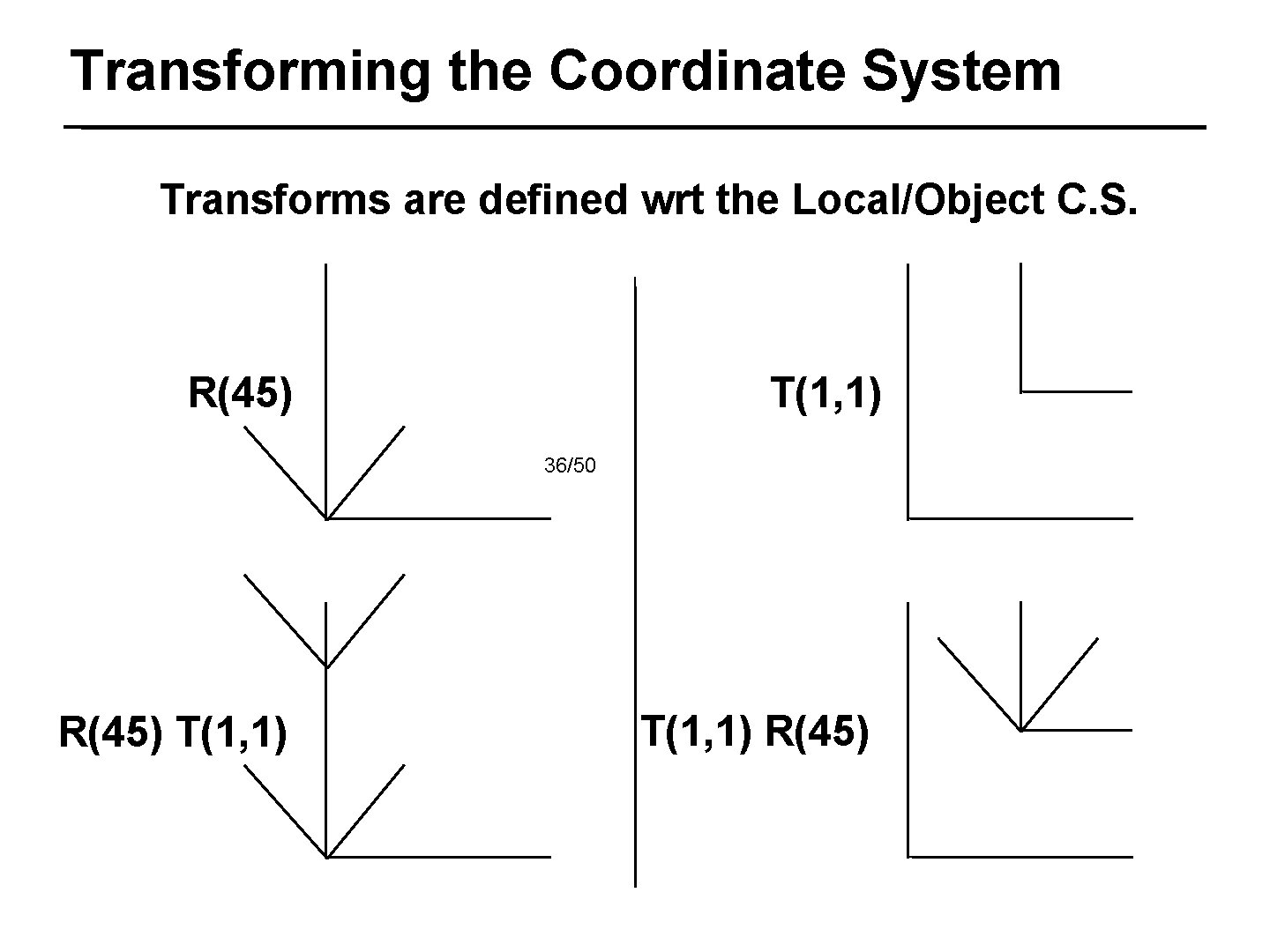
Transforming the Coordinate System Transforms are defined wrt the Local/Object C. S. R(45) T(1, 1) 36/50 R(45) T(1, 1) R(45)

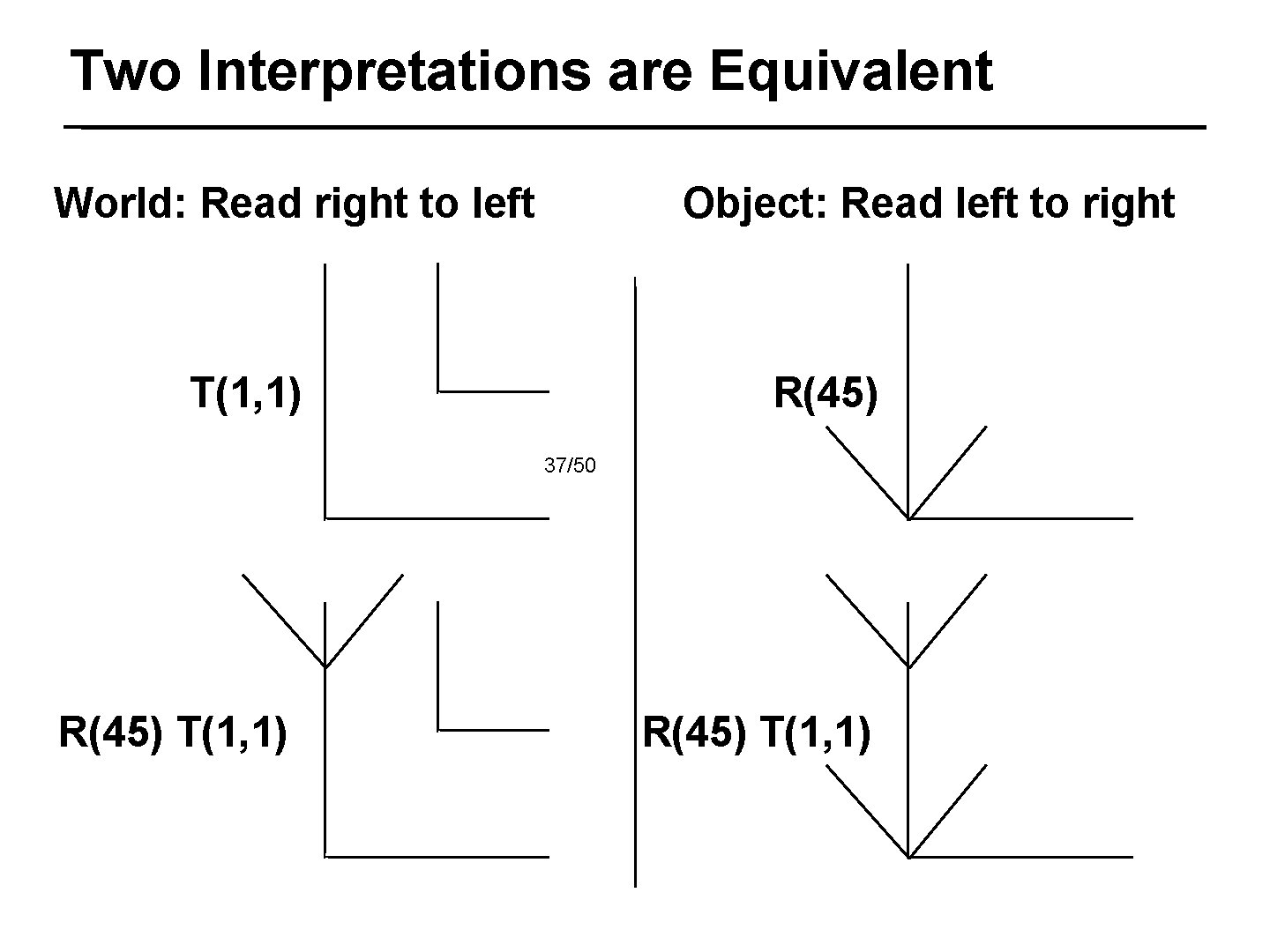
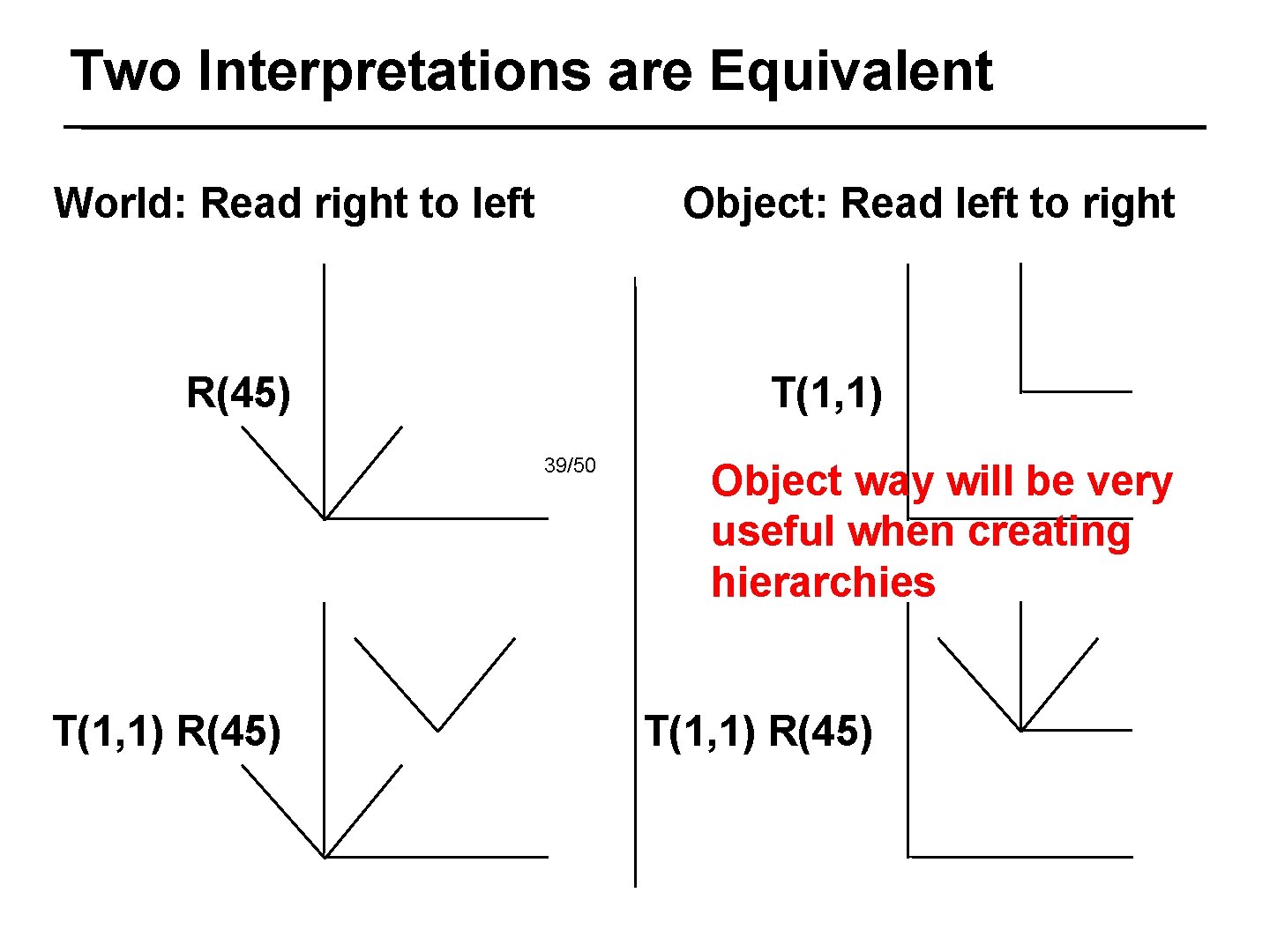
Two Interpretations are Equivalent World: Read right to left Object: Read left to right T(1, 1) R(45) 37/50 R(45) T(1, 1)

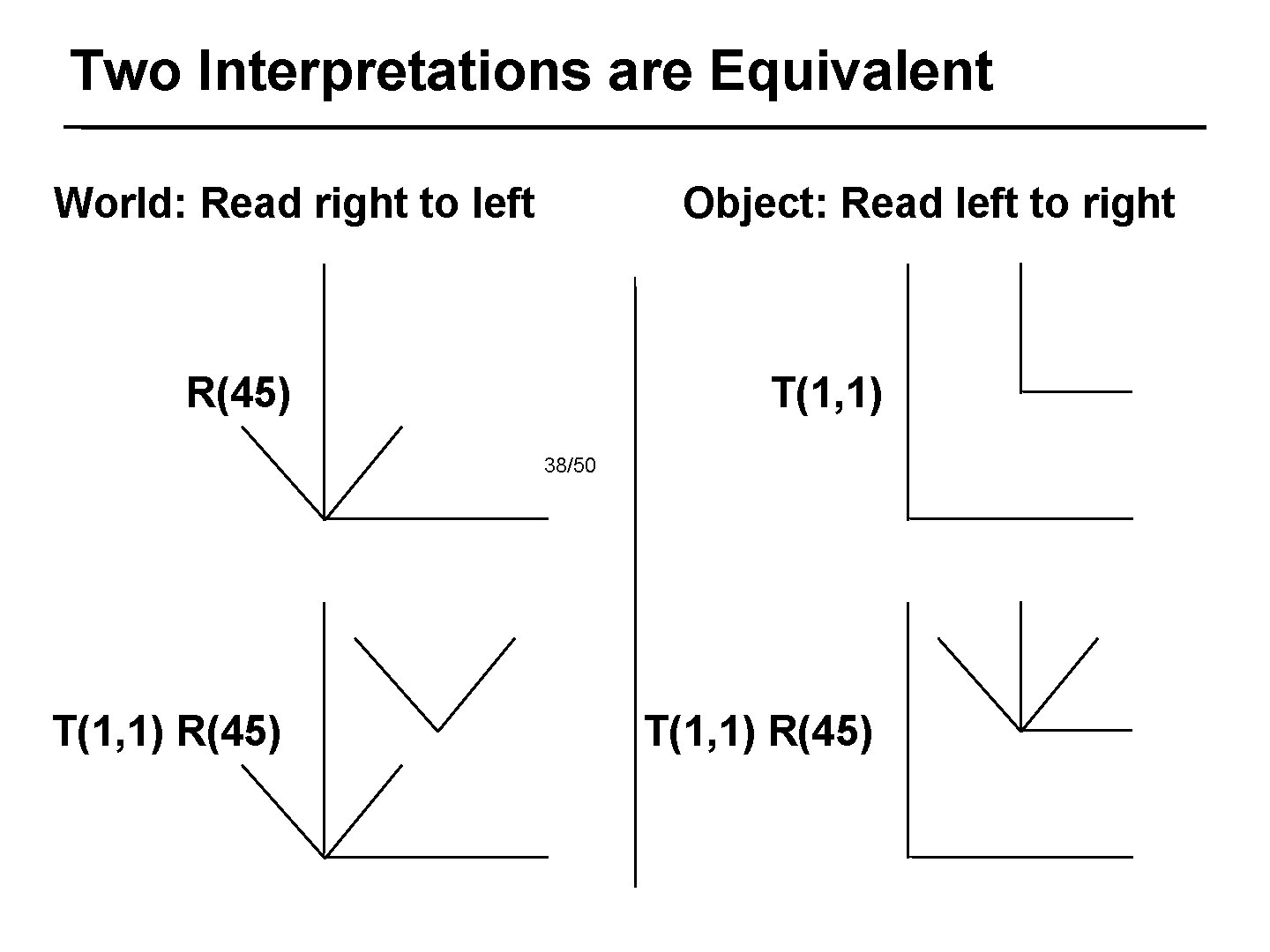
Two Interpretations are Equivalent World: Read right to left Object: Read left to right R(45) T(1, 1) 38/50 T(1, 1) R(45)

Two Interpretations are Equivalent World: Read right to left Object: Read left to right R(45) T(1, 1) 39/50 T(1, 1) R(45) Object way will be very useful when creating hierarchies T(1, 1) R(45)

Hierarchical Transformations 40/50

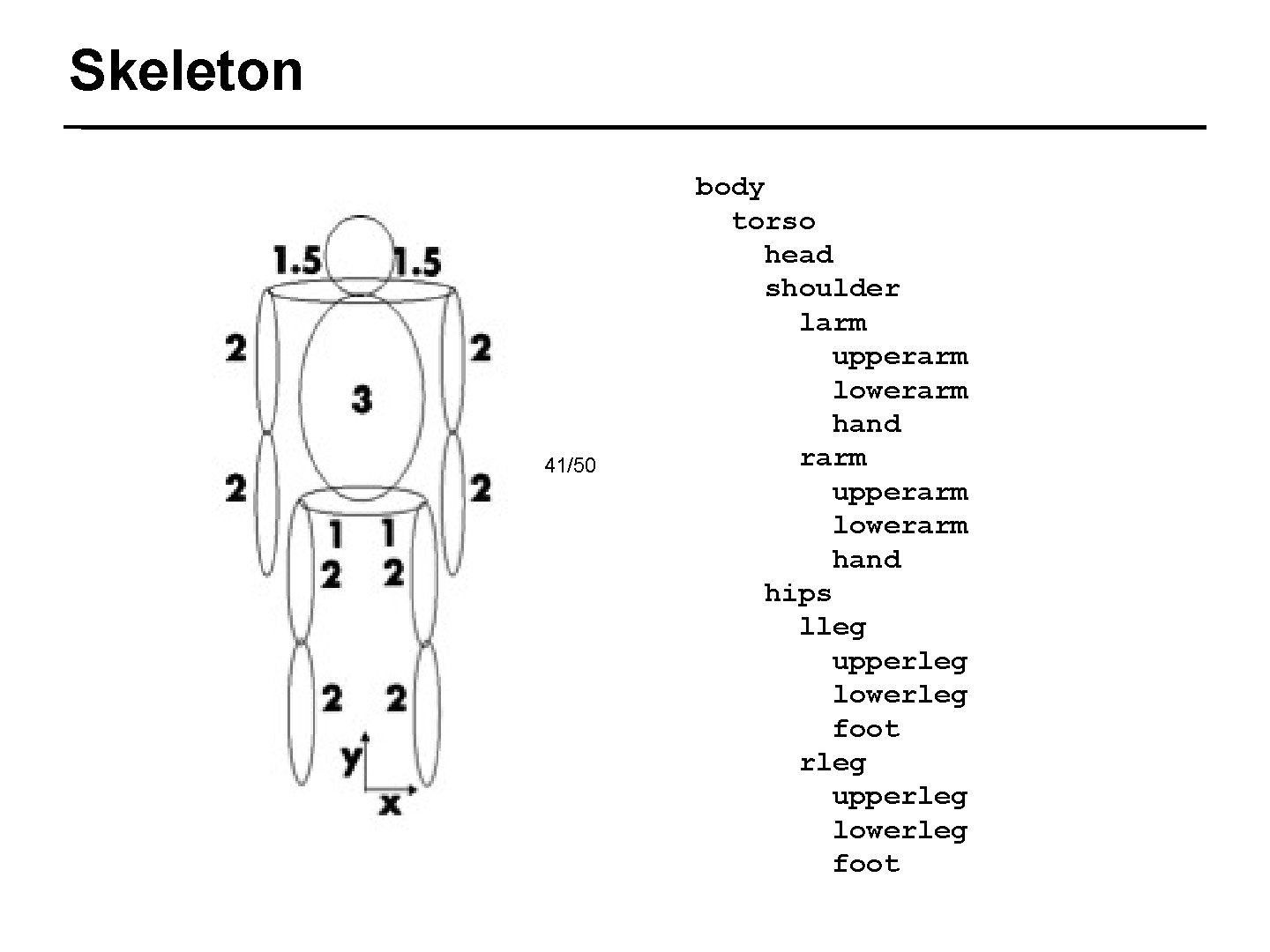
Skeleton 41/50 body torso head shoulder larm upperarm lowerarm hand rarm upperarm lowerarm hand hips lleg upperleg lowerleg foot rleg upperleg lowerleg foot

Skeletons and Linkages 1. Skeleton represents the hierarchy of an assembly of parts - The arm is made of an upper arm and a lower arm - Different parts may have the same shape, i. e. are “geometric instances” 42/50 2. Parts connected by joints - “The ankle joint is connected to the knee joint” - Different types of joints move differently e. g. a ball and socket joint, a linear actuator

How Linkages Work Lower levels of the hierarchy move when the upper levels moves ￭ e. g. moving the left shoulder moves the left arm and the left hand Motion in one sub-tree does not effect the position of a 43/50 part in another sub-tree ￭ e. g. moving the left hand does not effect the right hand

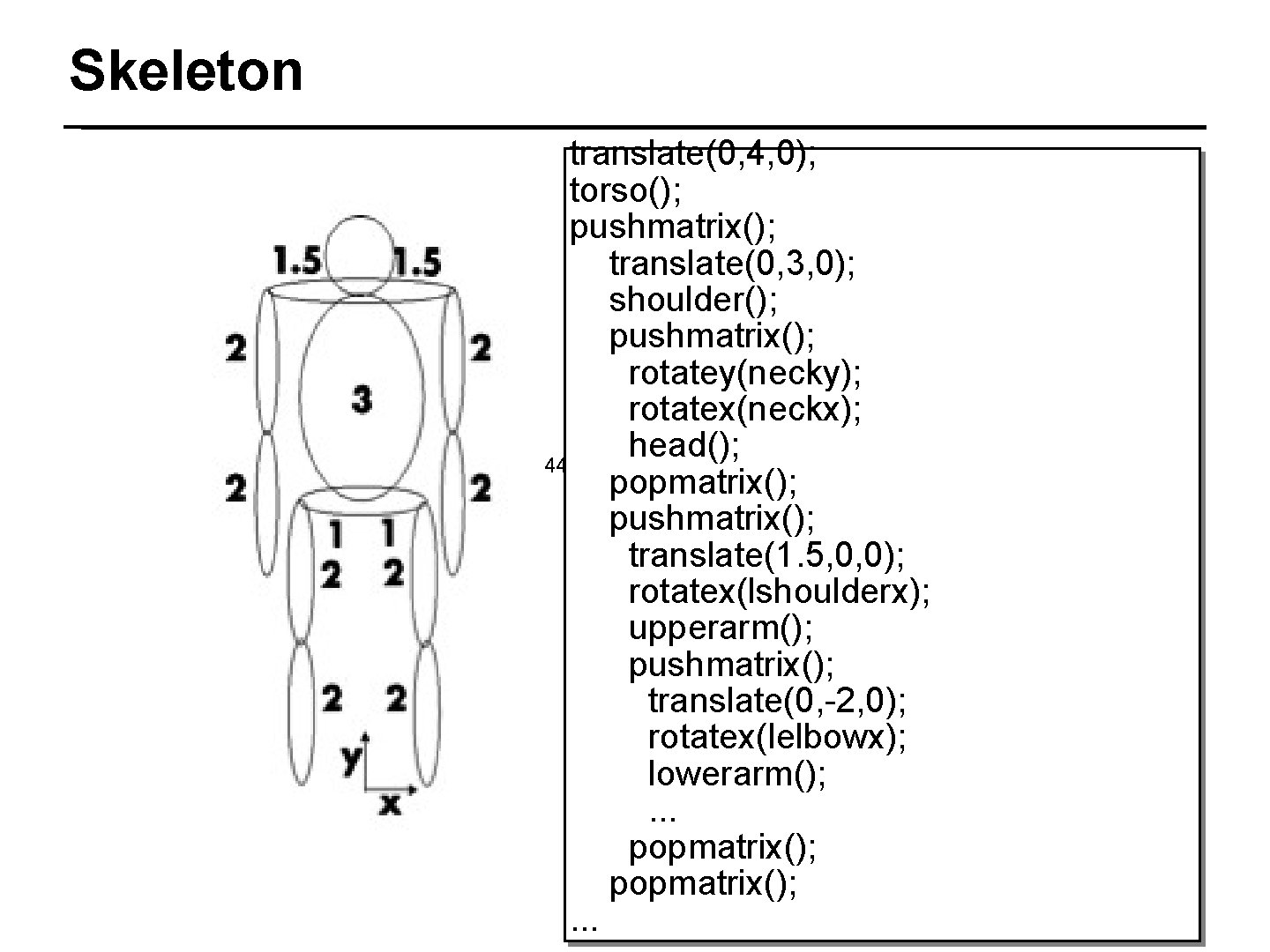
Skeleton translate(0, 4, 0); torso(); pushmatrix(); translate(0, 3, 0); shoulder(); pushmatrix(); rotatey(necky); rotatex(neckx); head(); 44/50 Text popmatrix(); pushmatrix(); translate(1. 5, 0, 0); rotatex(lshoulderx); upperarm(); pushmatrix(); translate(0, -2, 0); rotatex(lelbowx); lowerarm(); . . . popmatrix(); Pat Hanrahan, Fall 2011. . .

Open. GL 45/50

Current Transformation Matrix Open. GL maintains a current transformation matrix (CTM). All geometry is transformed by the CTM. 46/50 Transformation commands are concatenated onto the CTM on the right. CTM *= T This causes T to be applied before the old CTM

Open. GL Matrix Functions gl. Load. Identity( ) ￭ Set the transform matrix to the identity matrix gl. Load. Matrix( matrix M ) ￭ Replace the transform matrix with M 47/50 M ) gl. Mult. Matrix( matrix ￭ Multiplies transform matrix by CTM * M ￭ gl. Rotate, gl. Translate, gl. Scale etc. are just wrappers for gl. Mult. Matrix

Graphics Coordinate Frames Object ￭ Raw values as provided by gl. Vertex (ex. teacup centered at origin) World ￭ Object at final location in environment (ex. teacup 48/50 recentered to be on top of a table) Screen ￭ Object at final screen position

Open. GL Matrix Functions gl. Matrix. Mode( mode ) ￭ Sets which transformation matrix to modify ￭ GL_MODELVIEW: object to world transform ￭ GL_PROJECTION: world to screen transform ￭ CTM = GL_PROJECTION * GL_MODELVIEW 49/50 Why? May need to transform by one of these matrices for certain calculations like lighting. More on this latter.

Open. GL Matrix Stack Save and restore transformations gl. Push. Matrix ( ) ￭ Pushes the current matrix onto the top of the matrix stack gl. Pop. Matrix ( ) 50/50 ￭ Pops the matrix off the top of the matrix stack and loads it as the current matrix