CS 148 Introduction to Computer Graphics and Imaging

CS 148: Introduction to Computer Graphics and Imaging Triangles 1/27 CS 148 Lecture 3

How to draw a triangle on the screen Rasterization 2/27 CS 148 Lecture 3

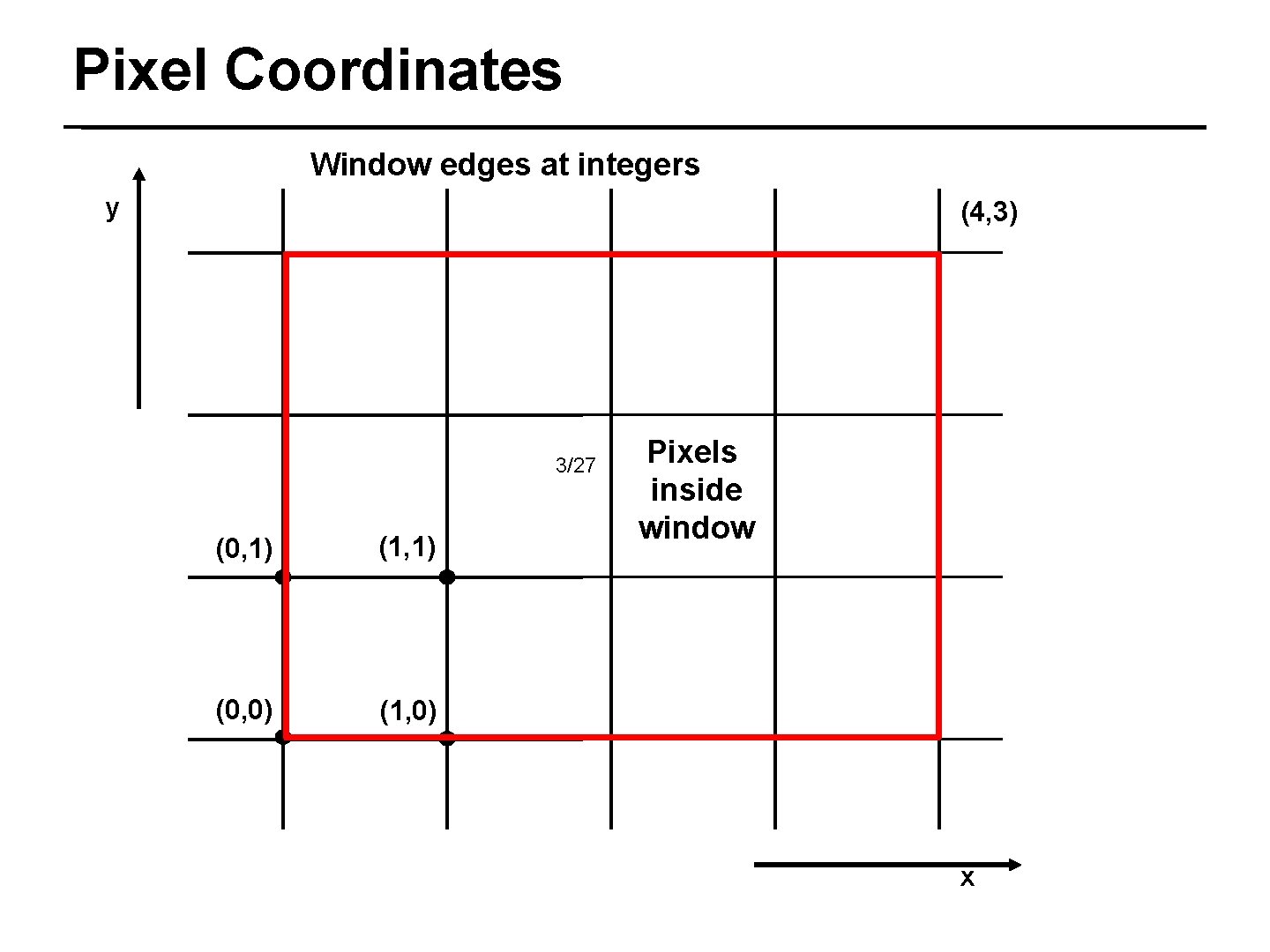
Pixel Coordinates Window edges at integers y (4, 3) 3/27 (0, 1) (1, 1) (0, 0) (1, 0) Pixels inside window x

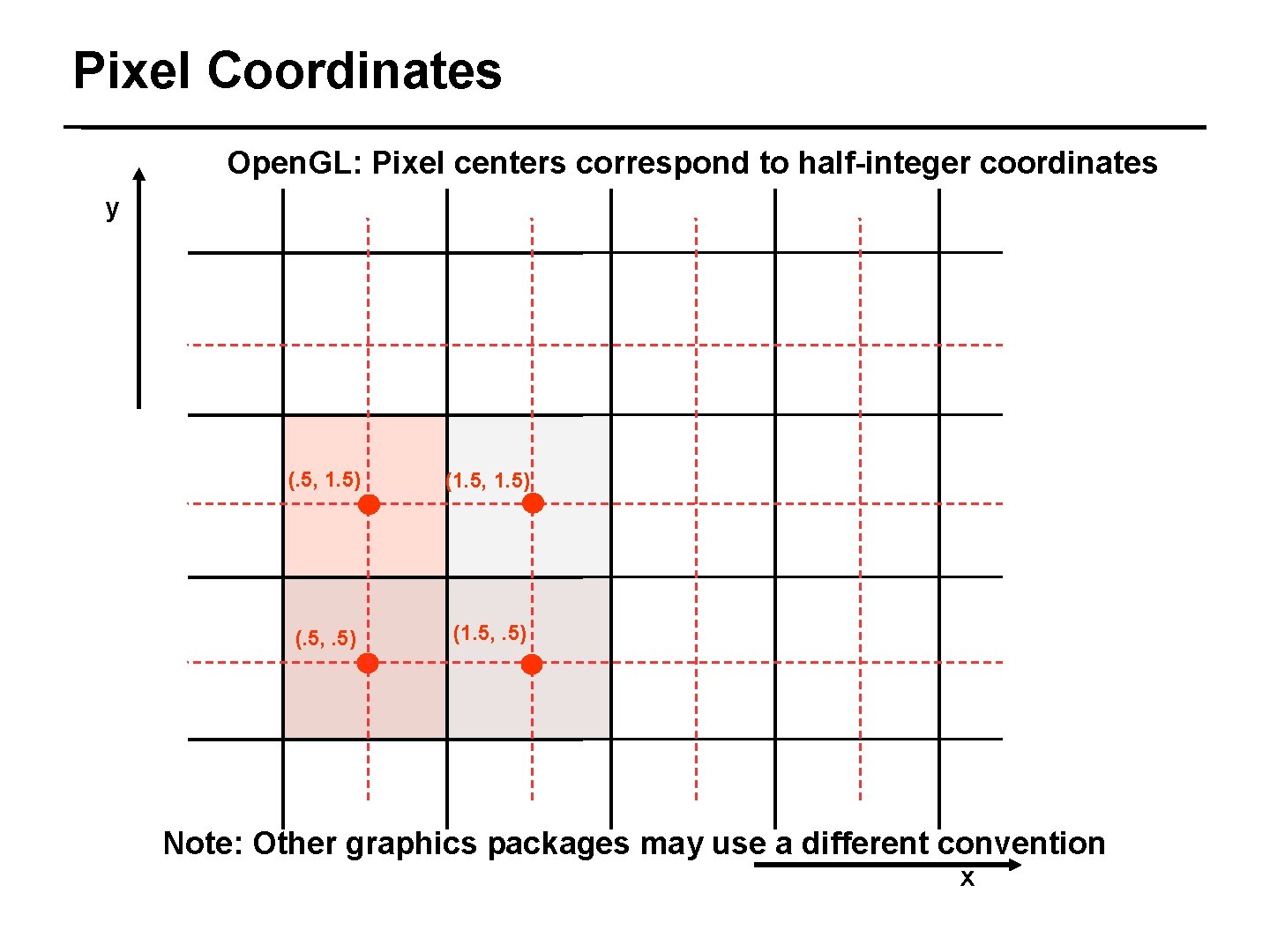
Pixel Coordinates Open. GL: Pixel centers correspond to half-integer coordinates y (. 5, 1. 5) (1. 5, 1. 5) (. 5, . 5) (1. 5, . 5) 4/27 Note: Other graphics packages may use a different convention x

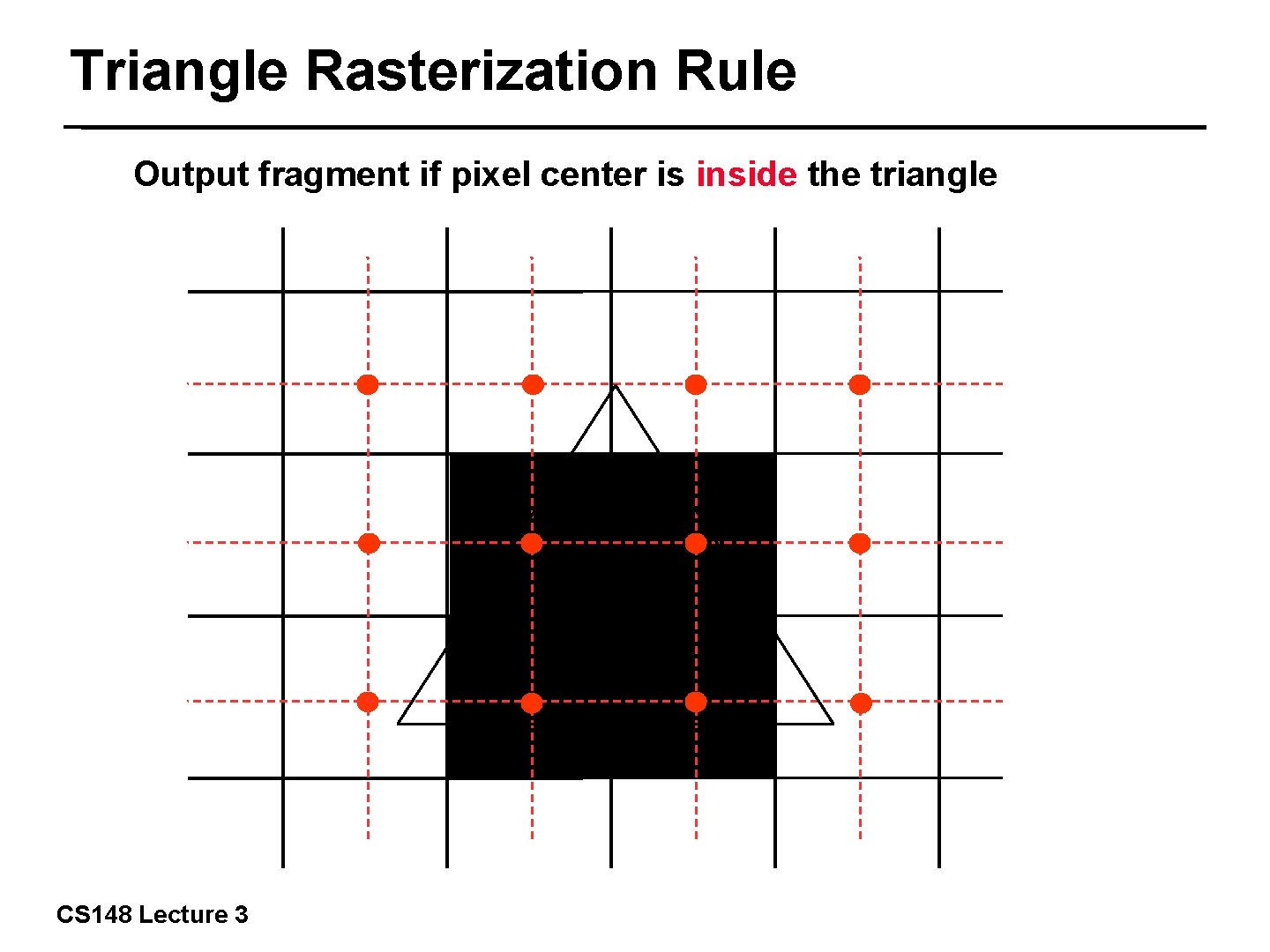
Triangle Rasterization Rule Output fragment if pixel center is inside the triangle 5/27 CS 148 Lecture 3

Triangle Rasterization v 0 rasterize( vert v[3] ) { for( int y=0; y<YRES; y++ ) 6/27 for( int x=0; x<XRES; x++ ) if( inside 3(v, x, y) ) fragment(x, y); } CS 148 Lecture 3 l 1 l 2 v 1 l 0 v 2

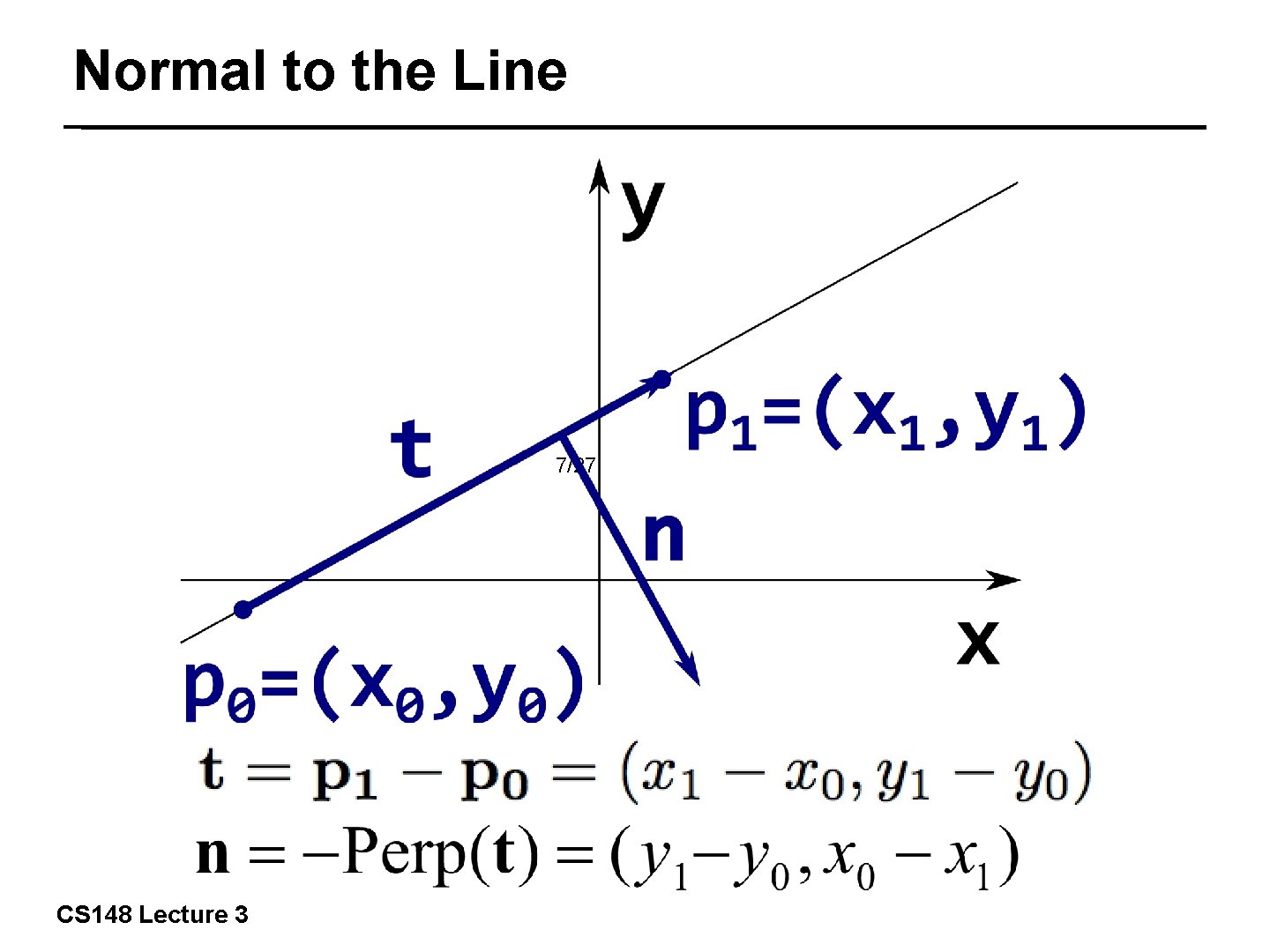
Normal to the Line 7/27 CS 148 Lecture 3

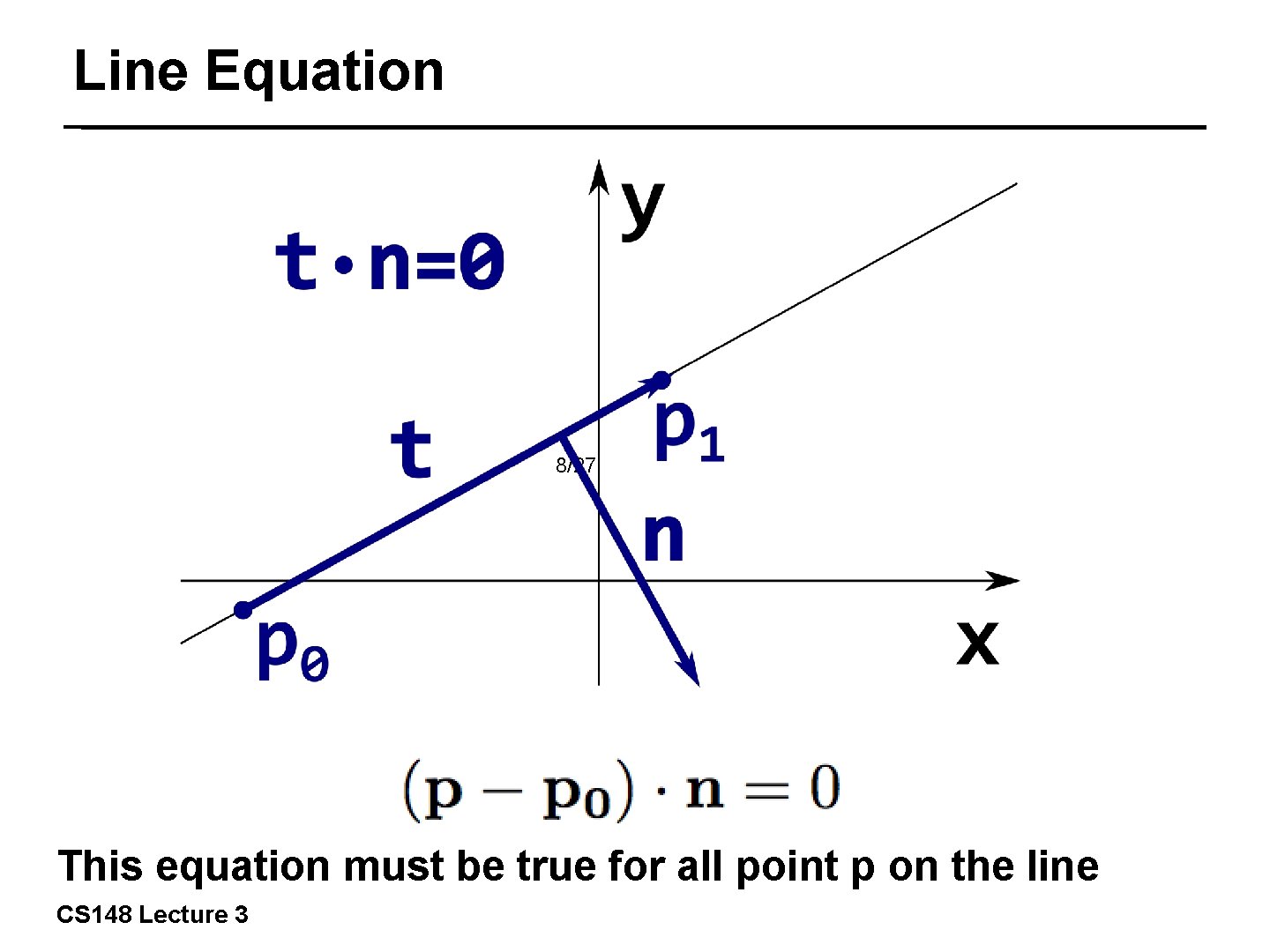
Line Equation 8/27 This equation must be true for all point p on the line CS 148 Lecture 3

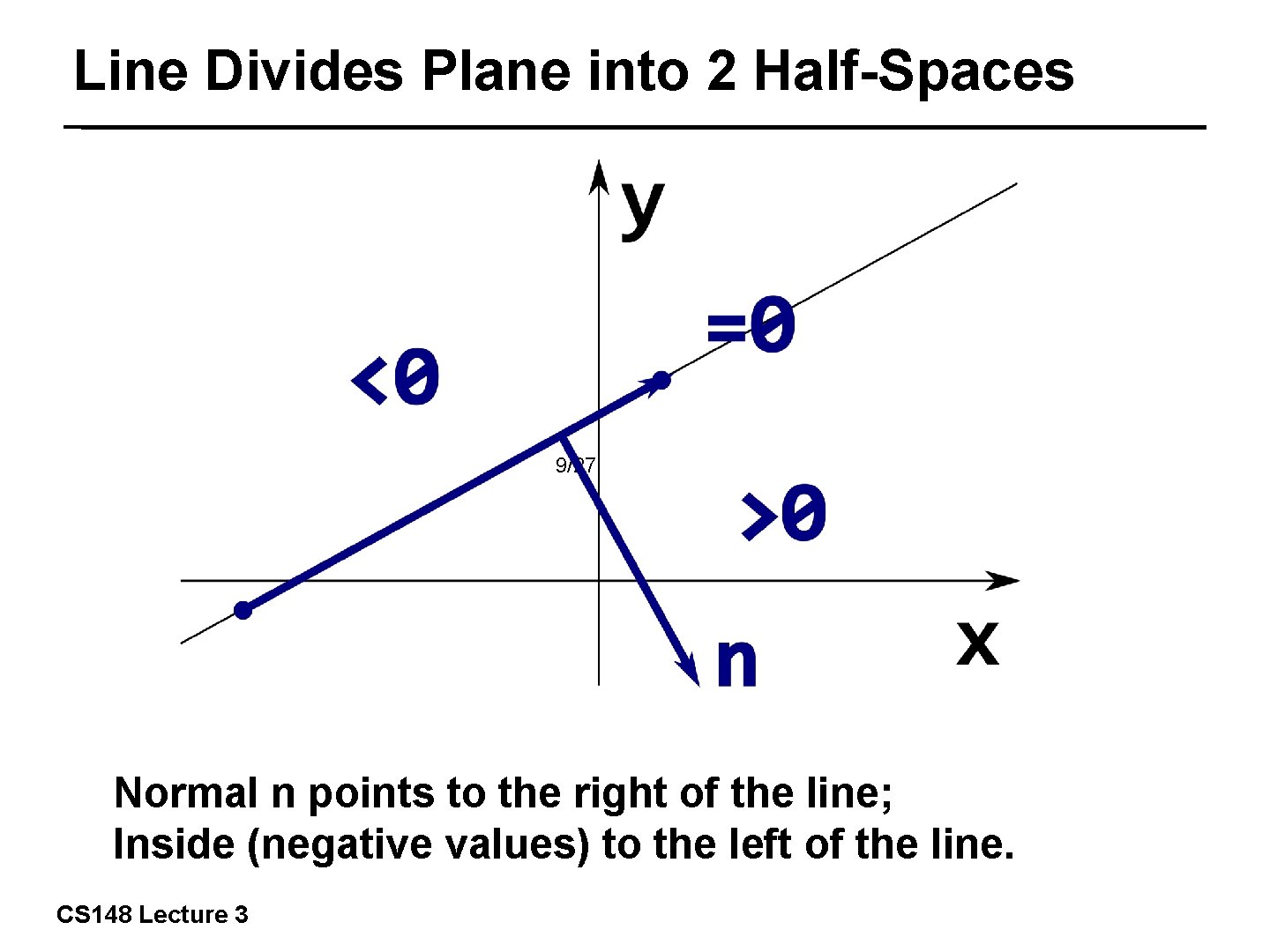
Line Divides Plane into 2 Half-Spaces 9/27 Normal n points to the right of the line; Inside (negative values) to the left of the line. CS 148 Lecture 3

Make a Line from Two Vertices makeline( vert& v 0, vert& v 1, line& l ) { l. a = v 1. y - v 0. y; l. b = v 0. x - v 1. x; l. c = -(l. a * v 0. x + l. b * v 0. y); } 10/27 l CS 148 Lecture 3 v 0 v 1

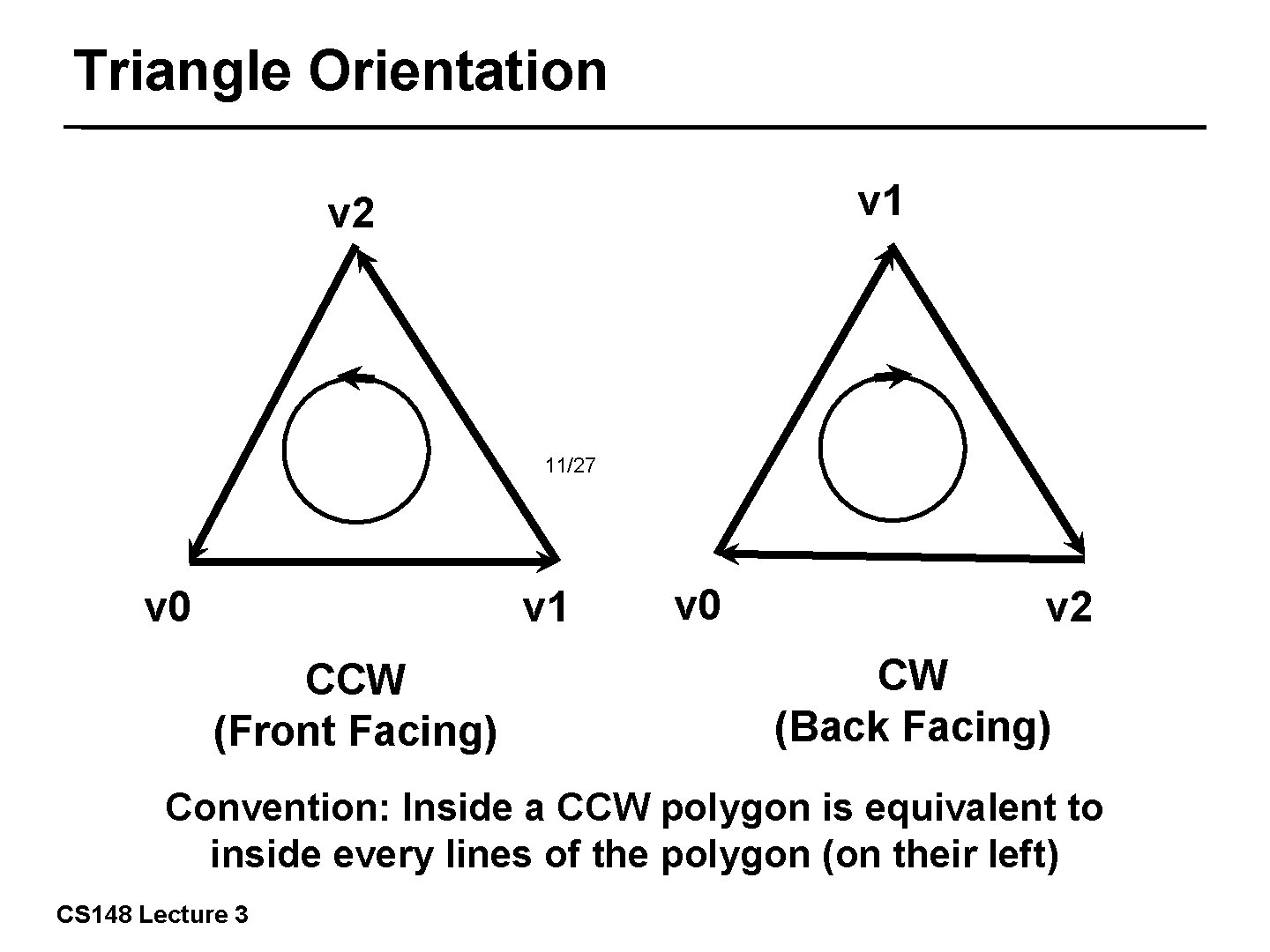
Triangle Orientation v 1 v 2 11/27 v 0 v 1 CCW (Front Facing) v 0 v 2 CW (Back Facing) Convention: Inside a CCW polygon is equivalent to inside every lines of the polygon (on their left) CS 148 Lecture 3

Point Inside Triangle Test rasterize( vert v[3] ) { } line l 0, l 1, l 2; makeline(v[0], v[1], l 2); makeline(v[1], v[2], l 0); makeline(v[2], v[0], l 1); 12/27 for( y=0; y<YRES; y++ ) { for( x=0; x<XRES; x++ ) { e 0 = l 0. a * x + l 0. b * y + l 0. c; e 1 = l 1. a * x + l 1. b * y + l 1. c; e 2 = l 2. a * x + l 2. b * y + l 2. c; if( e 0<=0 && e 1<=0 && e 2<=0 ) fragment(x, y); } } CS 148 Lecture 3 v 0 l 1 l 2 v 1 l 0 v 2

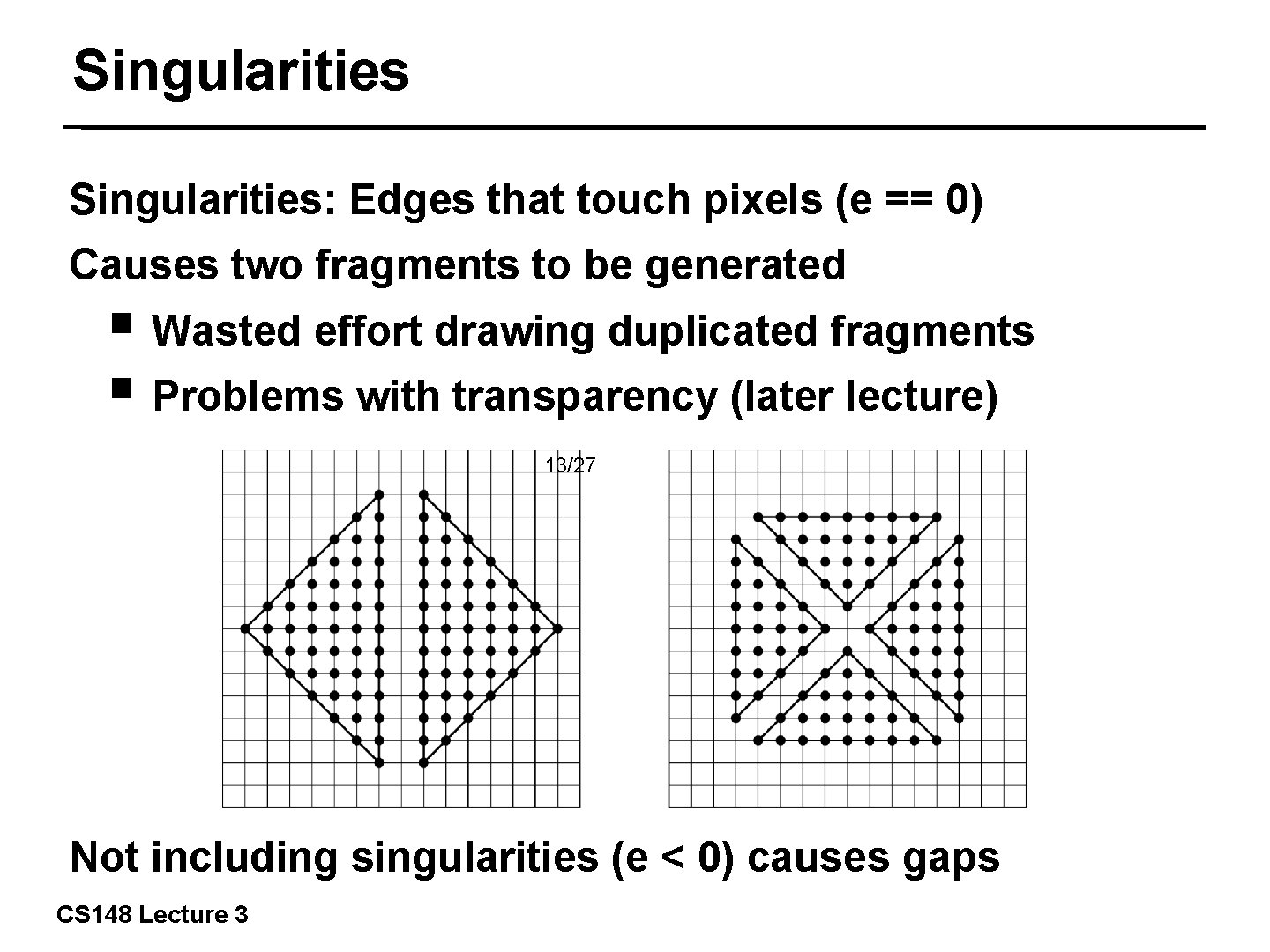
Singularities: Edges that touch pixels (e == 0) Causes two fragments to be generated ￭ Wasted effort drawing duplicated fragments ￭ Problems with transparency (later lecture) 13/27 Not including singularities (e < 0) causes gaps CS 148 Lecture 3

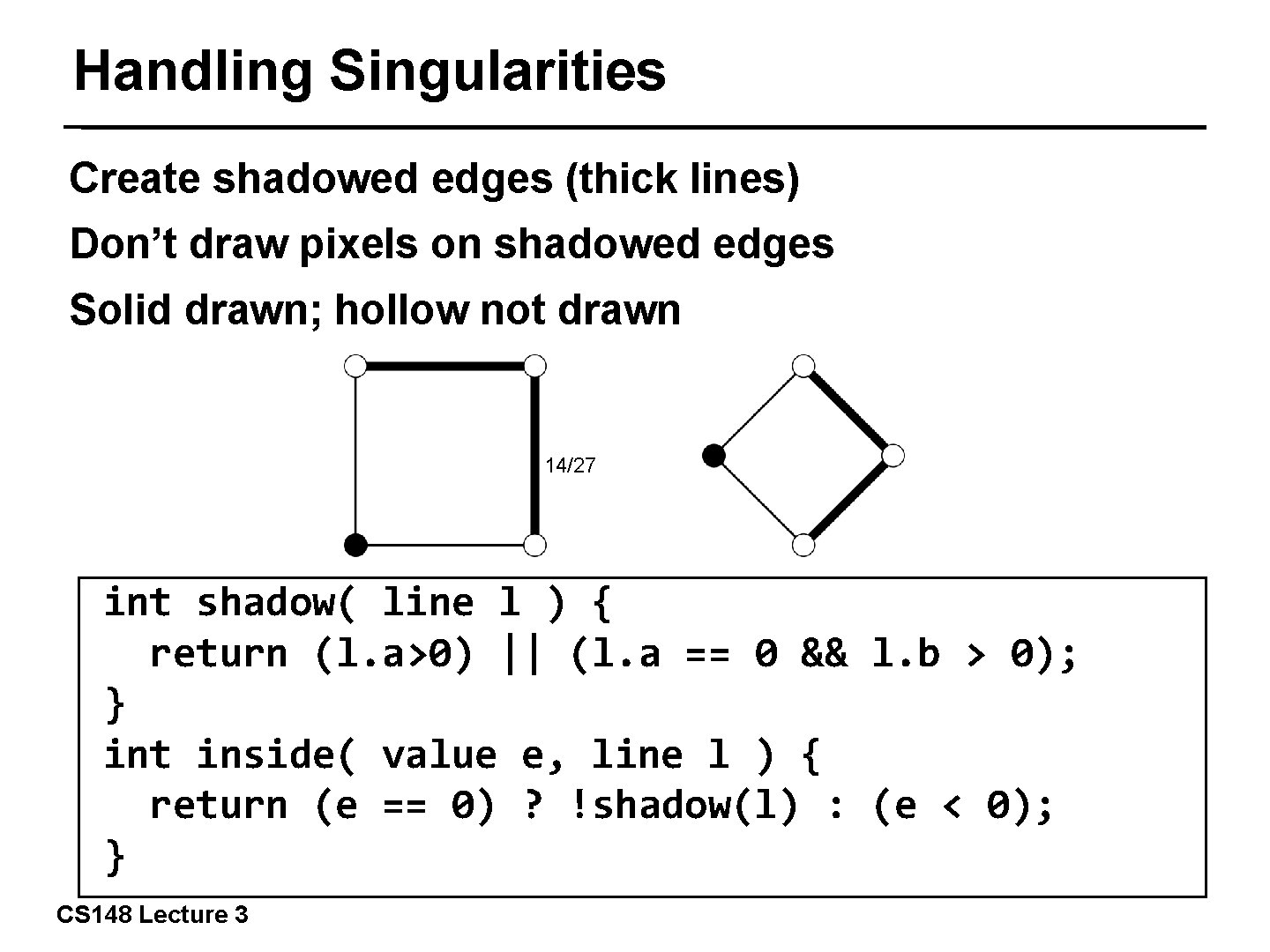
Handling Singularities Create shadowed edges (thick lines) Don’t draw pixels on shadowed edges Solid drawn; hollow not drawn 14/27 int shadow( line l ) { return (l. a>0) || (l. a == 0 && l. b > 0); } int inside( value e, line l ) { return (e == 0) ? !shadow(l) : (e < 0); } CS 148 Lecture 3

Better Point Inside Triangle Test rasterize( vert v[3] ) { } v 0 l 2 l 1 line l 0, l 1, l 2; makeline(v[0], v[1], l 2); v 2 v 1 l 0 makeline(v[1], v[2], l 0); makeline(v[2], v[0], l 1); 15/27 for( y=0; y<YRES; y++ ) { for( x=0; x<XRES; x++ ) { e 0 = l 0. a * x + l 0. b * y + l 0. c; e 1 = l 1. a * x + l 1. b * y + l 1. c; e 2 = l 2. a * x + l 2. b * y + l 2. c; if( inside(e 0, l 0)&&inside(e 1, l 1)&&inside(e 2, l 2) ) fragment(x, y); } } CS 148 Lecture 3

Compute Bounding Rectangle (BBox) bound 3( vert v[3], bbox& b ) { b. xmin = ceil(min(v[0]. x, v[1]. x, 16/27 b. xmax = ceil(max(v[0]. x, v[1]. x, b. ymin = ceil(min(v[0]. y, v[1]. y, b. ymax = ceil(max(v[0]. y, v[1]. y, } v[2]. x)); v[2]. y)); Calculate tight bound around the triangle Round coordinates upward (ceil) to the nearest integer CS 148 Lecture 3

Compute Bounding Rectangle (BBox) bound 3( vert v[3], bbox& b ) { b. xmin = ceil(min(v[0]. x, v[1]. x, 17/27 b. xmax = ceil(max(v[0]. x, v[1]. x, b. ymin = ceil(min(v[0]. y, v[1]. y, b. ymax = ceil(max(v[0]. y, v[1]. y, } Tested points indicated by filled circles Don’t need to test hollow circles CS 148 Lecture 3 v[2]. x)); v[2]. y));

More Efficient Bounding Box Version rasterize( vert v[3] ) { } bbox b; bound 3(v, b); line l 0, l 1, l 2; makeline(v[0], v[1], l 2); makeline(v[1], v[2], l 0); makeline(v[2], v[0], l 1); 18/27 for( y=b. ymin; y<b. ymax, y++ ) { for( x=b. xmin; x<b. xmax, x++ ) { e 0 = l 0. A * x + l 0. B * y + l 0. C; e 1 = l 1. A * x + l 1. B * y + l 1. C; e 2 = l 2. A * x + l 2. B * y + l 2. C; if( inside(e 0, l 0)&&inside(e 1, l 1)&&inside(e 2, l 2) ) fragment(x, y); } } CS 148 Lecture 3

Interpolation Convert discrete values to a continuous function by filling 19/27 in “in between” values CS 148 Lecture 3

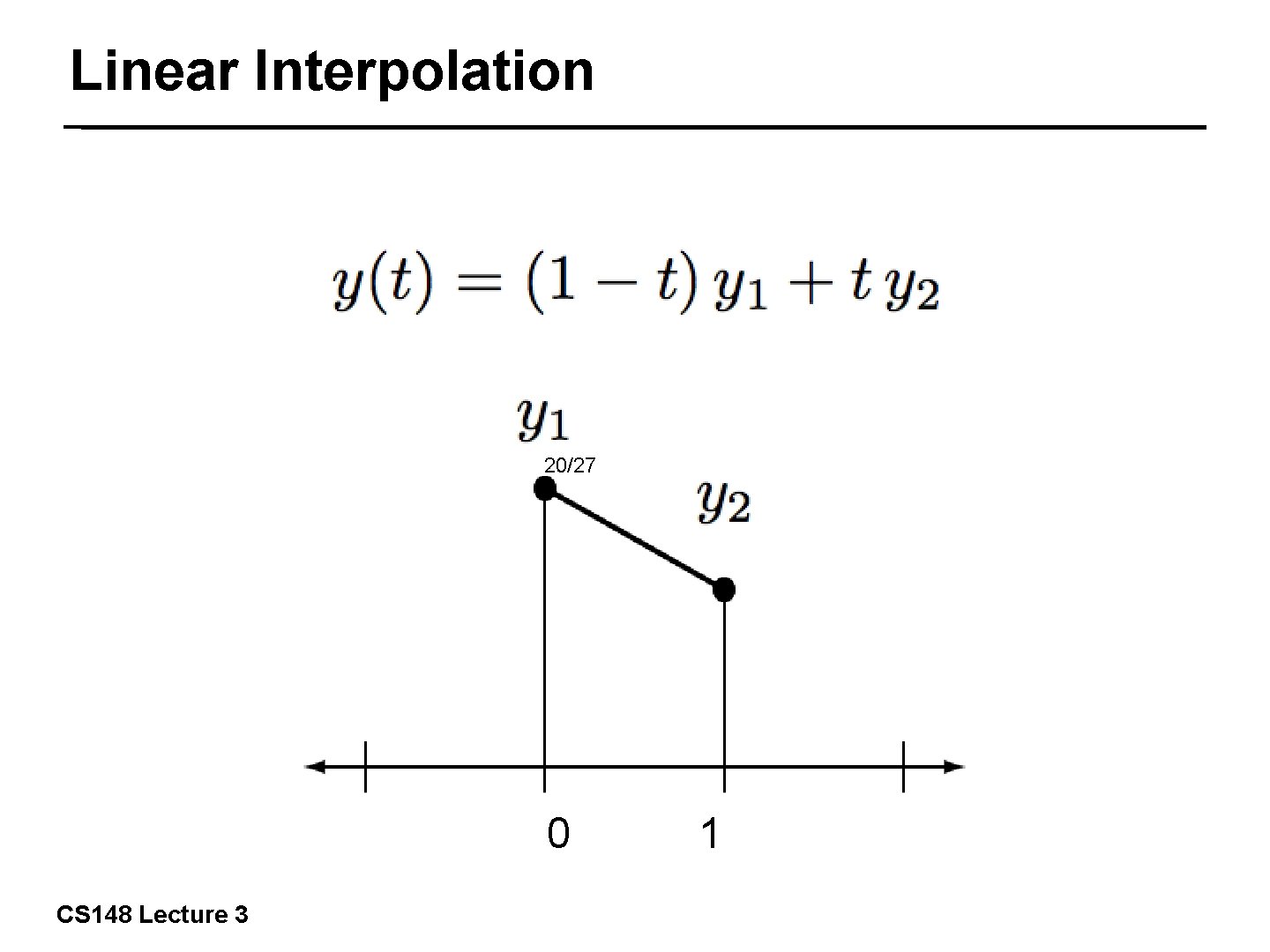
Linear Interpolation 20/27 0 CS 148 Lecture 3 1

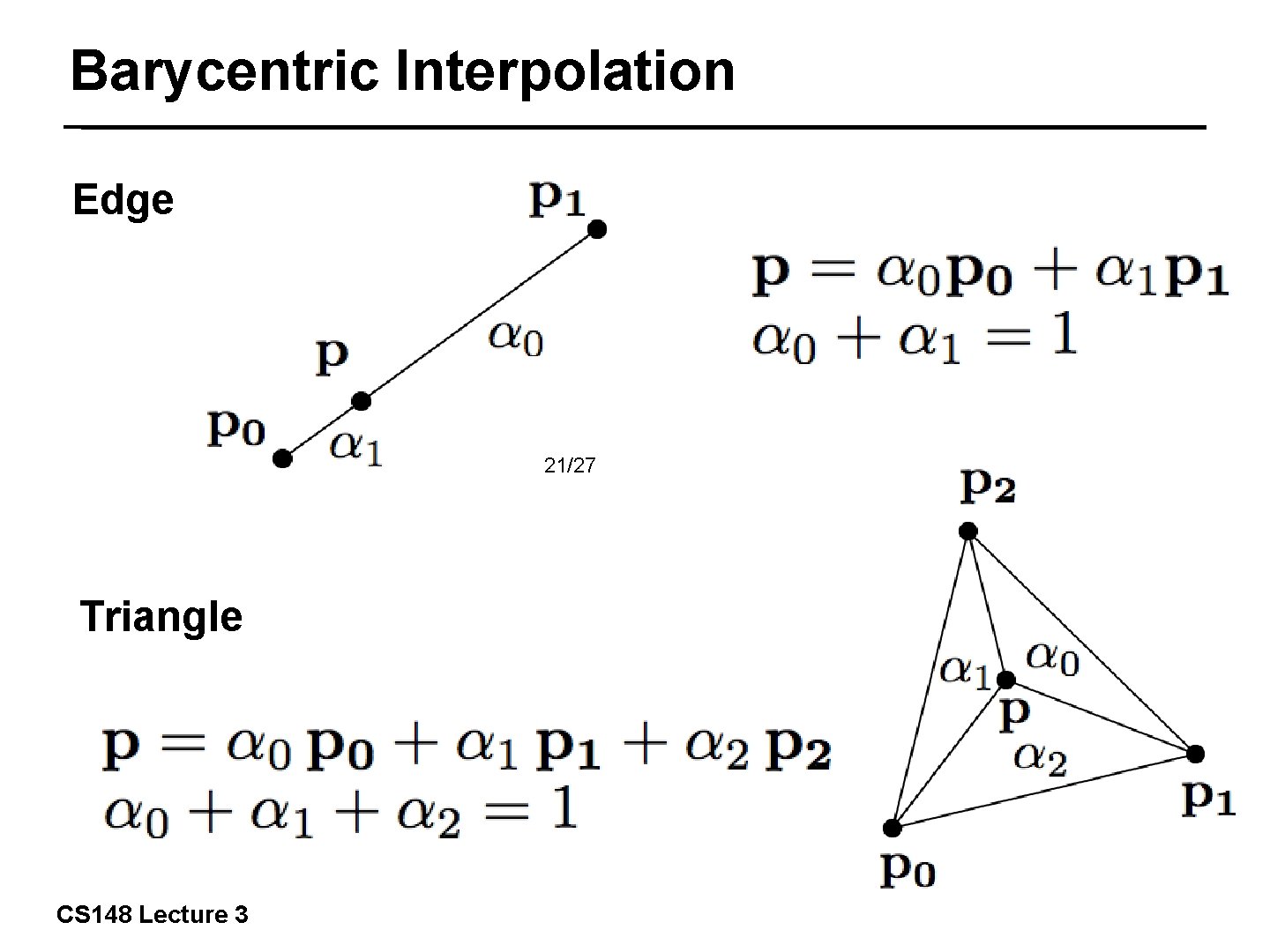
Barycentric Interpolation Edge 21/27 Triangle CS 148 Lecture 3

Barycentric Interpolation on Triangles Can be used to interpolate colors r = a 0 r 0 + a 1 r 1 + a 2 r 2 g = a 0 g 0 + a 1 g 1 + a 2 g 2 b = a 0 b 0 + a 1 b 1 + a 2 b 2 22/27 texture coordinates Can be used to interpolate u = a 0 u 0 + a 1 u 1 + a 2 u 2 v = a 0 v 0 + a 1 v 1 + a 2 v 2 Can be used to interpolate z or depth z = a 0 z 0 + a 1 z 1 + a 2 z 2 Can be used to interpolate normals… CS 148 Lecture 3

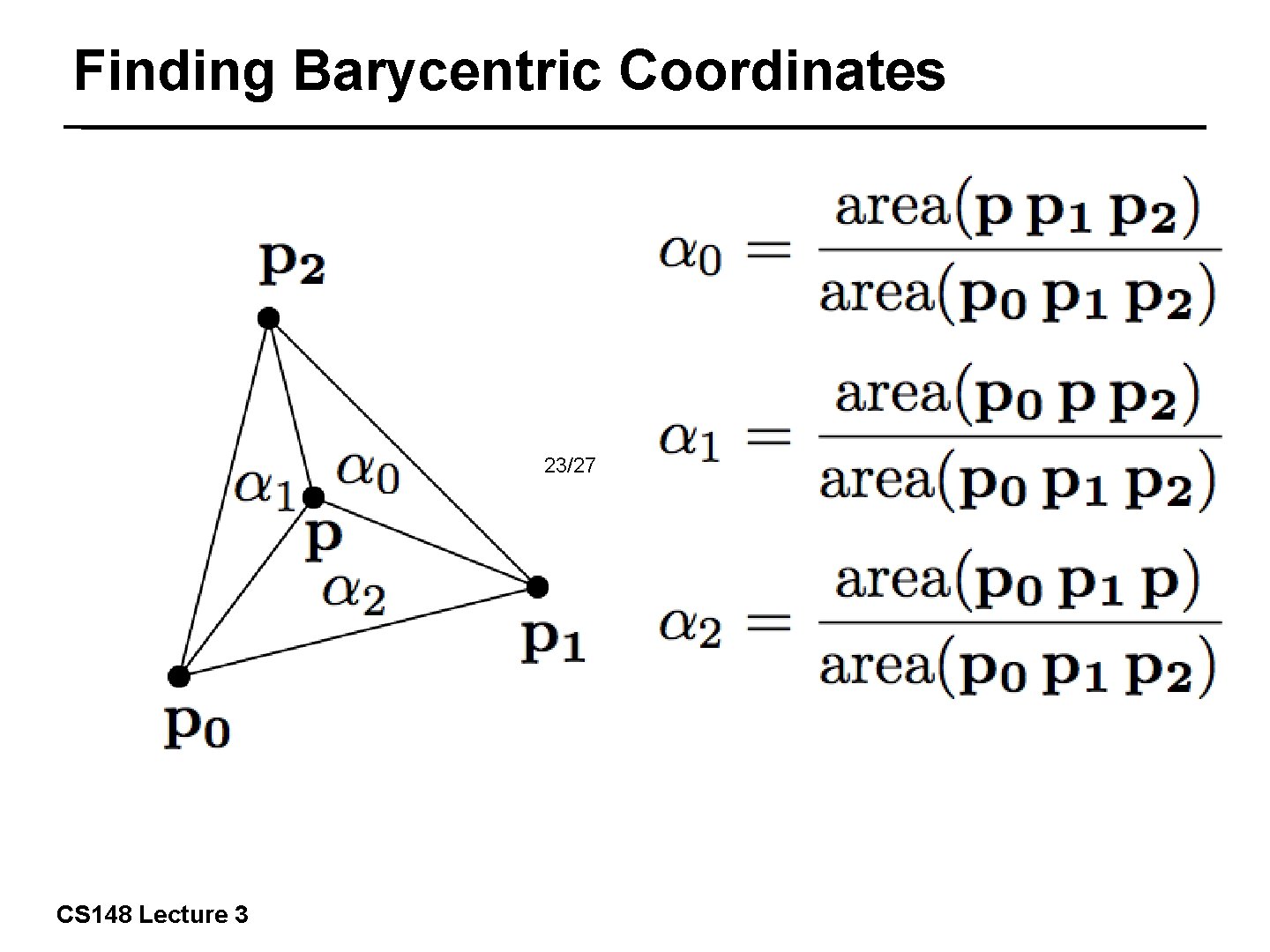
Finding Barycentric Coordinates 23/27 CS 148 Lecture 3

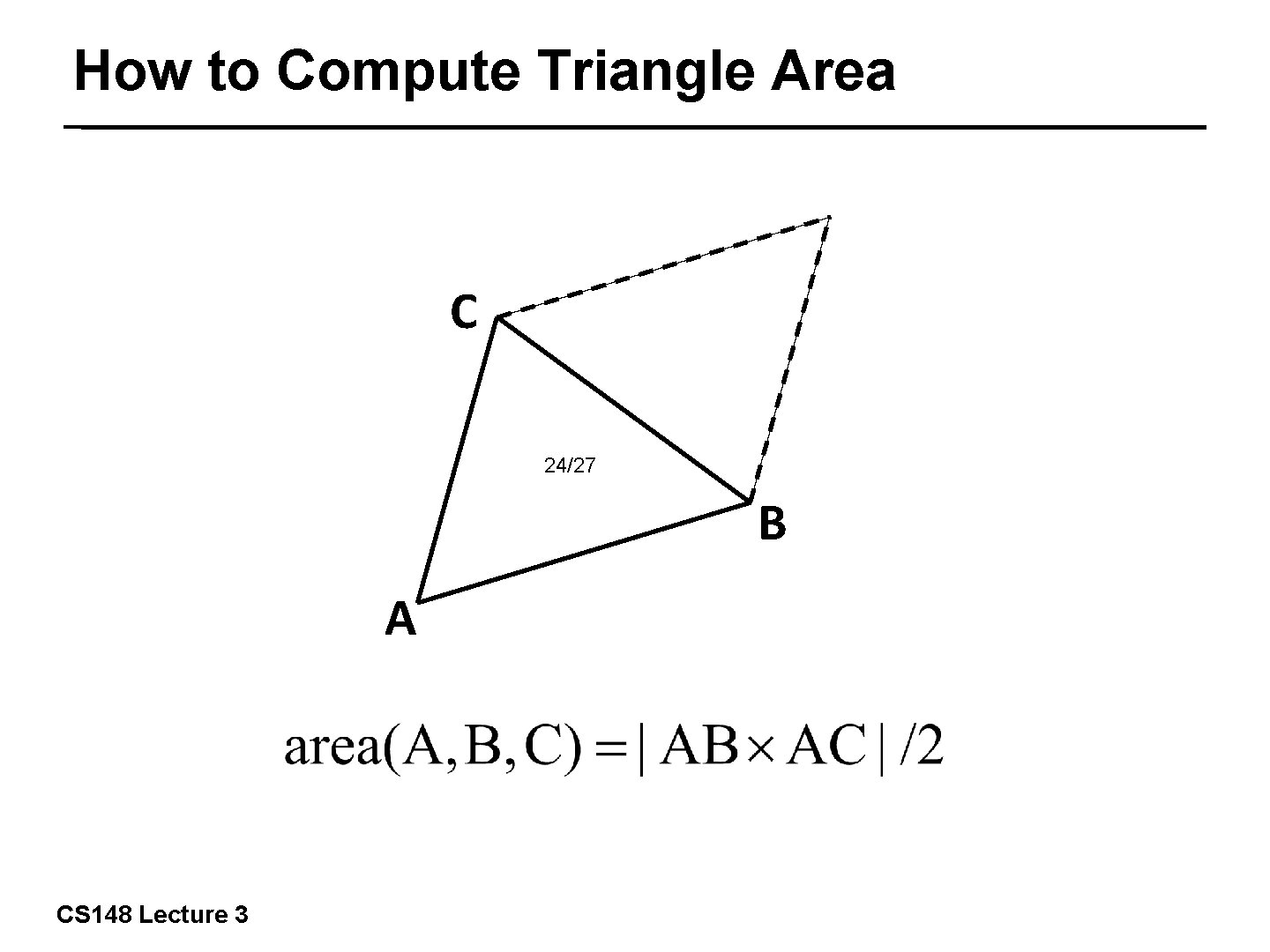
How to Compute Triangle Area C 24/27 B A CS 148 Lecture 3

Barycentric Coordinates: Linear System 25/27 Determinant of matrix is equal to zero if the points are co-linear CS 148 Lecture 3

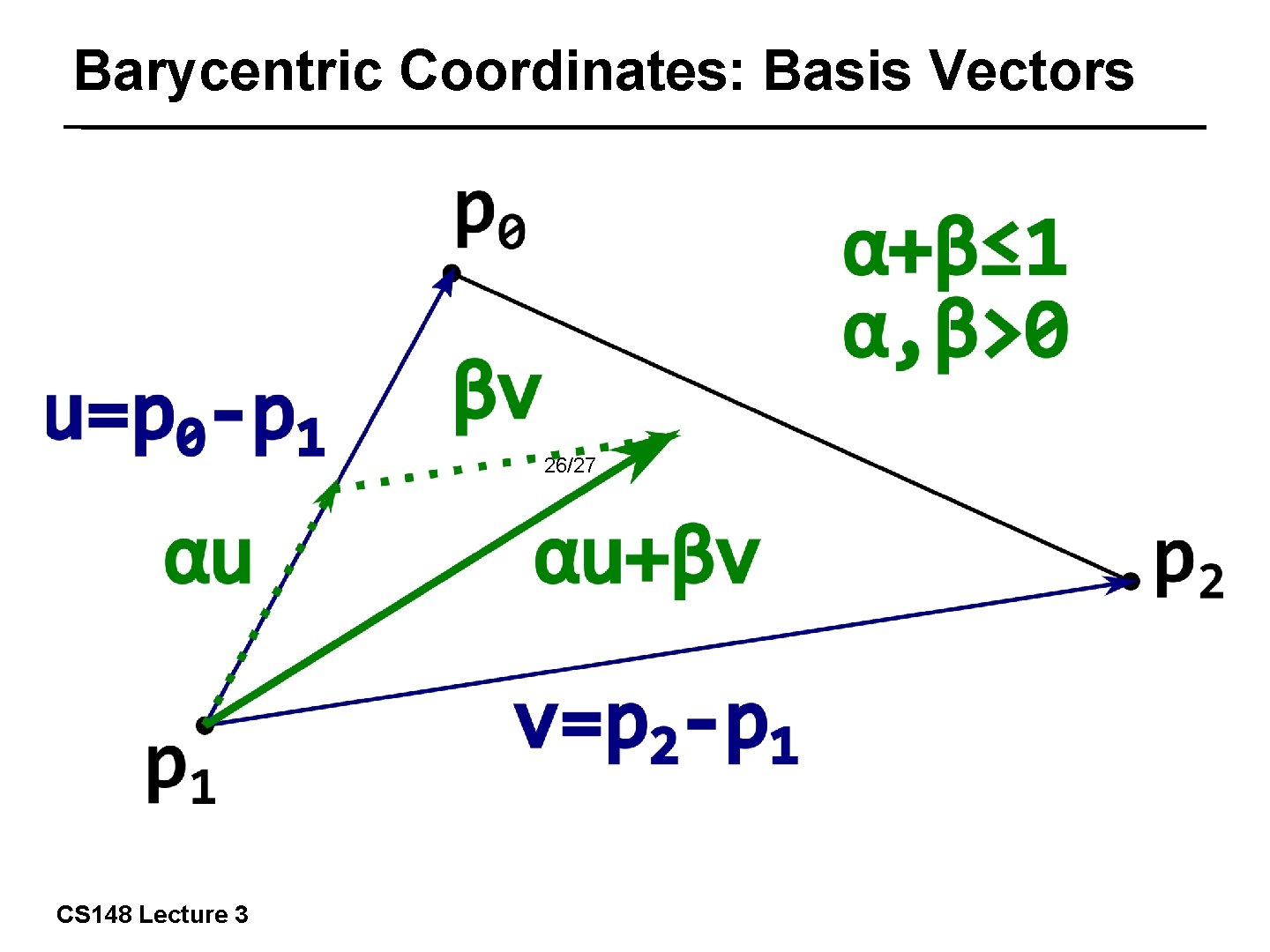
Barycentric Coordinates: Basis Vectors 26/27 CS 148 Lecture 3

Barycentric Coordinates vs. Basis Vector Coordinates A point p inside triangle p 0 p 1 p 2 can be expressed using barycentric coordinates as Point p can also be expressed in the basis vector 27/27 coordinates (of last slide as) Therefore, we get the relations CS 148 Lecture 3